Sandau R. Digital Airborne Camera: Introduction and Technology

Подождите немного. Документ загружается.

4.2 Optics and Mechanics 163

b = f (H, T, P) (4.2-6)

Thus the lens must be sufﬁciently robust to withstand all these inﬂuences in

order to produce a sufﬁciently sharp image under real or hypothetical conditions.

A modern treatment of the thermal problem, especially the quantitative treatment of

non-stationary thermal conditions, can be found in Leica (2003).

4.2.10.2 Transmitting Power and f-Number

Photogrammetric lenses often bear cryptic designations such as 15/4 UAGS or 30/4

NATS in the case of Leica. Whereas the ﬁrst number, here 15, indicates the focal

length in cm, the second number is the f-number, which is a measure of the transmit-

ting power of a lens, i.e., the light taken up by the objective lens. As shown earlier

on, the numerical aperture NA or NA’ forms part of this parameter. The f-number is

deﬁned as:

f # = 1/(2 ·NA



) = s



/(2 · Y

) (4.2-7)

If an image is set to inﬁnity, f# becomes f/(2 · Y

) = f/A, where A is the diameter

of EP (the entrance pupil). The smaller the f-number, the “faster” the optical system,

i.e., the greater its transmitting power. The opinion often voiced that the f-number is

calculated from the ratio of focal length to diameter of the ﬁrst lens is correct only

if the EP is situated in the front lens. This normally holds for normal photographic

lenses, but not for photogrammetric lenses. The aperture ratio is also commonly

used as the reciprocal value of the f-number. For example, if f = 100 mm and

A = 25 mm, then

A : f =1:4 or

100 mm

25 mm

= 4.

4.2.10.3 Angles on the Lens and Image Sides

Some characteristic optical operating parameters are dealt with below. But ﬁrst, let

us consider Fig. 4.2-9, which shows the ideal case of an individual lens in which

both pupils coincide in the centre of the lens. Let the lens be set to “inﬁnity”, such

that the distance between the image plane and the centre of the lens is the focal

length f and let a circular object ﬁeld with diameter D be imaged on the image array

with diameter d. The rays drawn in the ﬁgure are the principal rays with which we

are familiar.

The intercept theorem applies

. (4.2-8)

The ratio f/h

corresponds to the image scale.

4.2 Optics and Mechanics 165

In the case of a square image d

= 2b

Thus, the square image is b × b, where b =



4.2.10.4 Example

The image diameter for the image array of a 4096 × 4096 matrix with a pixel pitch

of 9 μmmustbe

d =



2718 mm

≈ 52 mm

The ﬁeld of view (FOV) deﬁned by a line of a matrix or of a line detector of

length l is

FOV = 2arctan



l/2



(4.2-12)

Figure 4.2-11 shows how the ﬁeld of view FOV varies with the focal length. The

line is assumed to have a constant length of l =78 mm corresponding to a CCD line

with 12,000 elements and an element spacing x = 6.5 μm.

The stereo angle γ of a CCD line camera is dependent on the distance a of the

stereo lines from the “nadir line”, i.e., the line in the centre of the image directed

downwards (Fig. 4.2-12).

= arctan







. (4.2-13)

can be regarded more generally as the angle of convergence of two parallel

lines (Fig. 4.2-12). It can cause interference even in the case of closely packed lines.

In the case of CCD lines arranged side by side with ﬁlters for red, green and blue,

100

120

140

160

180

200

Focal length in mm

FOV in degrees

Fig. 4.2-11 Field of view depends on the focal length f of the lens (cross-track detector dimension

is 78 mm

 12,000 elements (σ = 6.5 μm)

168 4 Structure of a Digital Airborne Camera

100

0 20 40 60 80 100 120 140 160 180

Swath width S in km

Focal length in mm

Fig. 4.2-15 Swath width S as a function of the focal length at the given constant ﬂight altitude

= 3 km; the cross-track detector dimension is 78 mm (12,000 pixels @ σ = 6.5 μm)

Figure 4.2-15 illustrates the swath width, which is a function of the focal length

f, for a ﬂight altitude of h

= 3,000 m.

For a given line length l and focal length f, the swath width-to-altitude ratio

instantly tells us the swath width associated with a given ﬂight altitude

. (4.2-20)

The stereo base length B, i.e., the distance a of the CCD lines (see Fig. 4.2-10)

projected on to the ground, is expressed by

B = a ·

(4.2-21)

For a given line spacing a and focal length f, the base length-to-altitude ratio

instantly tells us the base length associated with a given ﬂight altitude.

(4.2-22)

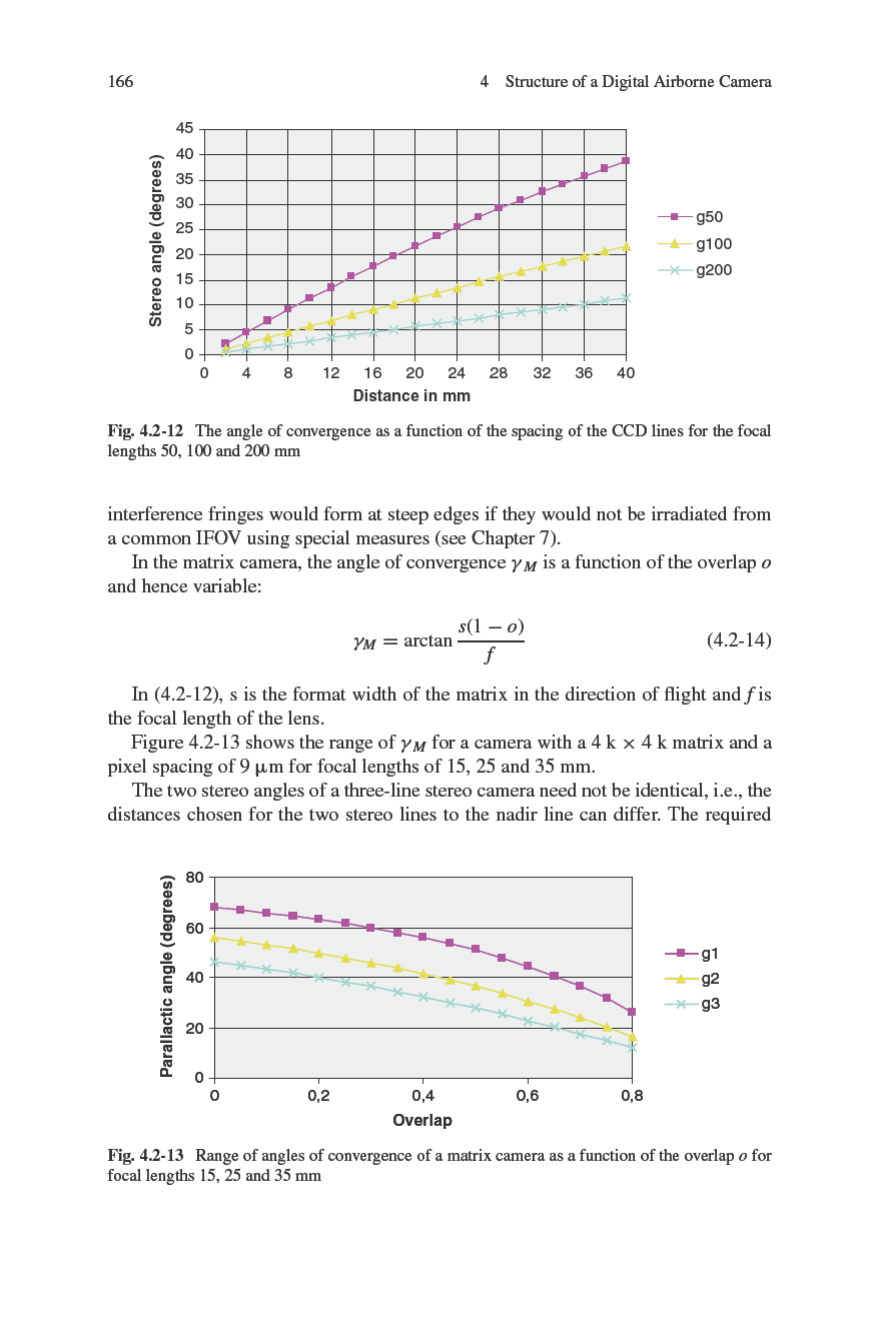
4.2.10.6 Ground Pixel Size and GSD

The size of the projection of a CCD element on the ground is dependent on the focal

length and the ﬂight altitude (Fig. 4.2-16):

X = x ·

(4.2-23)

The GSD is the sampling distance on the ground, if we imagine the pixel centre

point as the sampling point. If the sampling points in the direction of ﬂight are

selected such that there are no gaps between the lines, then GSD

= GSD

= X.

The GSD selected in direction x can differ from that in direction y. Rectangular

ground pixels in which GSD

>GSD

are obtained when the integration time in

4.2 Optics and Mechanics 171

Table 4.2-1 summarizes the quantities deﬁned and discussed in this section.

Table 4.2-1 List of key geometric characteristics of an airborne lens for digital airborne cameras

with focal length f: detector extent l

in the cross-ﬂight direction, size of a square detector element

x and line distance a in the case of a line camera; and detector extent s in the direction of ﬂight and

overlap o in the case of the matrix camera

FOV 2 · arctan





IFOV 2 · arctan



x/2



Swath width Sl

Pixel size on the ground Xx·

Stereo angle γ

arctan





Stereo angle γ

arctan



s(1−o)



Base length Ba·

Swath width to altitude ratio S/H

Base length to altitude ratio B/H

s(1−o)

Total ﬁeld of view TFOV 2 ·arctan



d/2



Image array diameter d 2 · f ·tan

TFOV

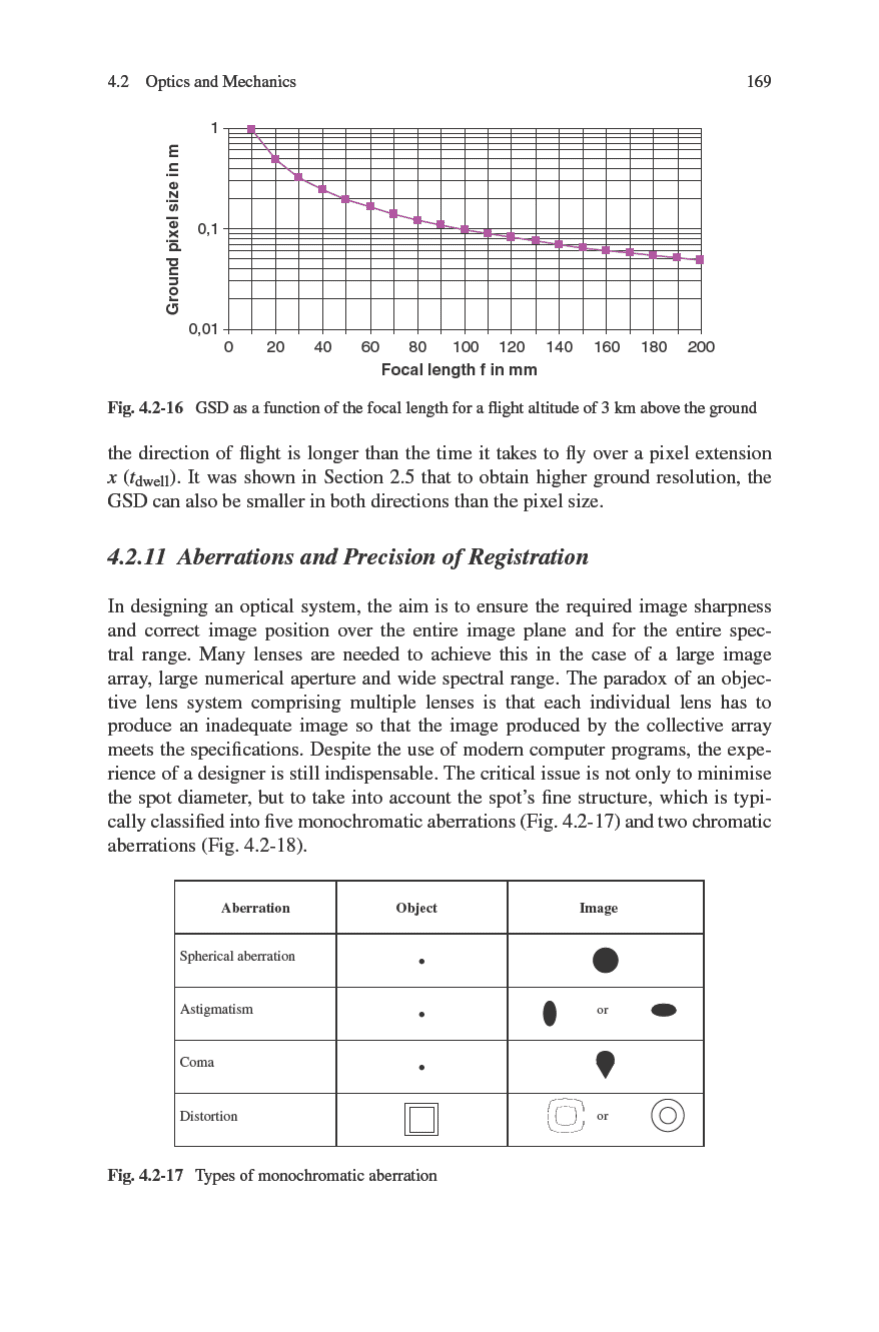
4.2.12 Radiometric Characteristics

The radiometric characteristics of a lens include the spectral transmittance as a func-

tion of the wavelength and the ﬁeld angle, the suppression of stray light and the

depolarisation of light.

4.2.12.1 Spectral Transmittance

The spectral transmittance of the lens depends on the absorption behaviour of the

glass materials and on the reﬂectivity of the glass surfaces. In general the bulk

absorption is not critical for glass in the visible and near infrared spectral range with

wavelengths below 1,000 nm, except for the blue spectral range with wavelengths

below 450 nm (Fig. 4.2-19). In this range the lead-free glass now produced by all

major manufacturers has more absorption than the old types of glass containing

lead. This can cause serious problems for objectives with many lens elements.

The manufacturers therefore attempt to keep the transmission loss in limits using

special antireﬂection (AR) coatings on the surfaces of the glass elements. For this

172 4 Structure of a Digital Airborne Camera

Fig. 4.2-19 Spectral transmission of Schott glass SF14 and K5 with a thickness of 25 mm

purpose we ﬁrst consider the normal incidence of light on an uncoated glass sur-

face. In air it reﬂects R = [(n-1)/(n+1)]

= 4%, if we select n = 1.5. For a lens with

22 glass-air transitions the total transmission would be reduced from 1 to 0.96

0.40, that is less than half of the incident light is lost. It is therefore necessary to

develop coatings with a reﬂectance of <1% over the entire spectral range and for

a wide angular range. These requirements are contradictory, making it necessary

to deposit in a vacuum a large number of coatings (up to 50) on each lens sur-

face. Each coating is only a few tens of nm thick, which requires expensive, fully

automated vacuum equipment, extensive experience and, above all, considerable

psychological strength on the part of the operators if the 49th coating exceeds the

tolerance!

The transmission measured on a large lens is shown in Fig. 4.2-20. It can be seen

that at an average transmission of 0.8 for 22 glass-air transitions, an AR factor of

1% has been achieved over a wide range of the spectrum and that, even in the blue

range, very good values were measured despite the material problems mentioned.

The consistency of the transmission over the ﬁeld angle range from 0

◦

to 35

◦

is to be

assessed as high overall, as it allows the full dynamic range of the electronic sensors

to be used.

4.2.13 Ideal Optical Transfer Function

From the consideration of the physics of optical systems that led to the term “spatial

bandwidth” product, we know that every optical system necessarily acts as a “spatial

ﬁlter”, that is, it can only transmit an object of a speciﬁc size with a ﬁnite spatial