Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking

84

HEINZ-DIETER SCHILLING

relative to the zonal-mean flow APE tendency

(-&/To)

is

Mz

-

(

Km)/(

KE)

m

The magnitude of

BCL

relative to the

eddy

APE

tendency

(-Am/To)

is

M,

-

(L,z/L&,x~/~)

-

It can be shown that

BCL

is of the same relative magnitude

as

BCL

if

w&

is

scaled

after Green (1970).

Hence,

Bl,

,

and also Bl, measure the relative strength of meridional heat

flux convergence. This in turn is a reflection of zonal-mean flow baroclinic

instability to long wave perturbations. From

M,

we

see

that increased

B1,

enhances the decrease of

A,.

Too

small values of

Bl,

would decrease the

energy support from this

reservoir. Likewise, strong baroclinic input favor-

ing the eddies would enhance

Bl,

-

KE/KT

since

KE

would increase and

KT

would decrease. On the other hand, the measure

M,

for eddy baroclinic

activity

is

proportional to

B1,-ln.

If

Bl,

is

very large (e.g., during the mature

stage) the importance of

BCL

for the eddies

is

small. Since L, counteracts this

effect, longer waves would

be

affected

only if

B1,

is very large, but dominant

shorter waves even in the

case

of moderate

B1,

.

These conclusions can be

drawn for

Bl

too.

Hence, the baroclinic energy exchange between

A,

and

KE

works like a negative feedback, controlled by

Bl

or Bl, . From this point

of

view linear instability theories

are

not able to predict the evolution of blocks

with strong peaked

Bl.

Are those linear theories able at least to model the

sharp increase of

Bl

or

Bl,

as

shown in Fig.

3?

Only theories with standing

waves as part of the mean flow ought to be considered, since otherwise

Bl-

KE/KT

is set to

be

very small according to the linear assumption.

Because of the standing waves

as

part

of

the basic

flow

we have

KE

2

KT

and L,

k

4L, from the beginning. According to Fig.

3

those theories have

to explain the doubling ofBl during the buildup period ofblock (about

4

days

long).

We can write

Bl=E(1

+ao)2/(1

-aoy-KE/KT

for

t=to

and

Bl(t0

+

4 days)

=

E(

1

+

YU~)~/(

I

-

y~yao)~

with

E

being a constant which cancels out. This

E

contains the number of

wave modes considered in the unstable wave packet, the number

of

pertur-

bations of the zonal-mean flow,

a

characteristic wavenumber, and the largest

standing wave amplitude.

The

amplification rate of the fastest growing mode

in the ultralong wave range is denoted by

y

=

exp(4 days/T,). Of course,

LJL, is nearly constant for that wave packet. The initial amplitude

a,,

ON

ATMOSPHERIC

BLOCKING

TYPES

AND

NUMBERS

85

normalized with the basic flow amplitude, is assumed to

be

the same both for

the eddies and the zonal-mean flow perturbations. To yield

Bl(t,

+

4

days)/

BI

=

2

as

in Fig.

3,

the amplification rate

y

must

be

at least

2.55, 1.74,

and

1.46

for

a,

=

0.1,

0.2,

and 0.3, respectively. In other words, the e-folding

times

T, should be

4.2

days for

a,

=

0.1,7.2

days for

a,

=

0.2,

and

10.6

days

for

=

0.3.

These e-folding times correspond to the lower end oftheoretical

values for ultralong waves (e.g., about

10

days; after Sasamori and Young-

blut,

1981).

Therefore, in principle, this

type

of linear theory is able to

explain the evolution

of

BI

if the initial perturbation is in the upper range of

linearly consistent amplitudes. In fact,

a,

should

be

even larger since the

initial perturbation of the zonal-mean shear wind

is

a,/2

at best,

as

can be

computed from the results reported by Sasamori and Youngblut. Given this

we have to have an e-folding time of

6.5

days for

a,

=

0.3

to explain a

doubling of

BI.

The application of linear baroclinic instability theories is therefore a little

unsatisfactory in the

case

of

strong blocking. Moreover, those theories rely

strongly on the forcing (or standing wave). Therefore, a more natural ap-

proach would

be

a nonlinear baroclinic instabsty theory (e.g., Schilling,

1984),

which permits amplification rates Bl(t,

+

4

days)/Bl(to)

2

simply

by increasing

a,

above the limit demanded for linear theories. Moreover,

there

is

no more necessity for external forcing if not required.

5.

RELEVANT ENERGY

FLUXES

5.

I.

Correlation

Analysis

Synoptically defined blocking cases correspond not always to periods with

sharp peaking blocking numbers. Hence, it is useful to analyze the impact of

the energy conversions on the kinetic energy for the synoptic blocking situa-

tions. The seasonally stratified response of

K,

to various energy inputs

is

given in Fig. 8a-e. Again, the fluxes and energies are standardized to zero

mean and variance

1

[see

Eq.

(15)].

We begin with BTP, (Fig.

8c),

a measure of barotropic instability. Its

impact on

m

=

2-4

for all blocking days (Pacific plus Atlantic regions)

during

1967

-

1976

is significant

in

summer and winter (on a

95%

level), but

somewhat weaker in winter. Indeed, BTPZq4 can

be related to blocking wave

dynamics since

z

<

0

means that BTP, precedes

K,,,

. The significance for

m

=

1

and

m

=

5-8

is not

as

clear.

As

to the measure of baroclinic instability BCL, the correlation (Fig. 8d)

with

K,

during blocking days shows considerable impact on

all

scales, espe-

cially on the wavegroup

m

=

2

-

4.

Hansen (this volume) has chosen another

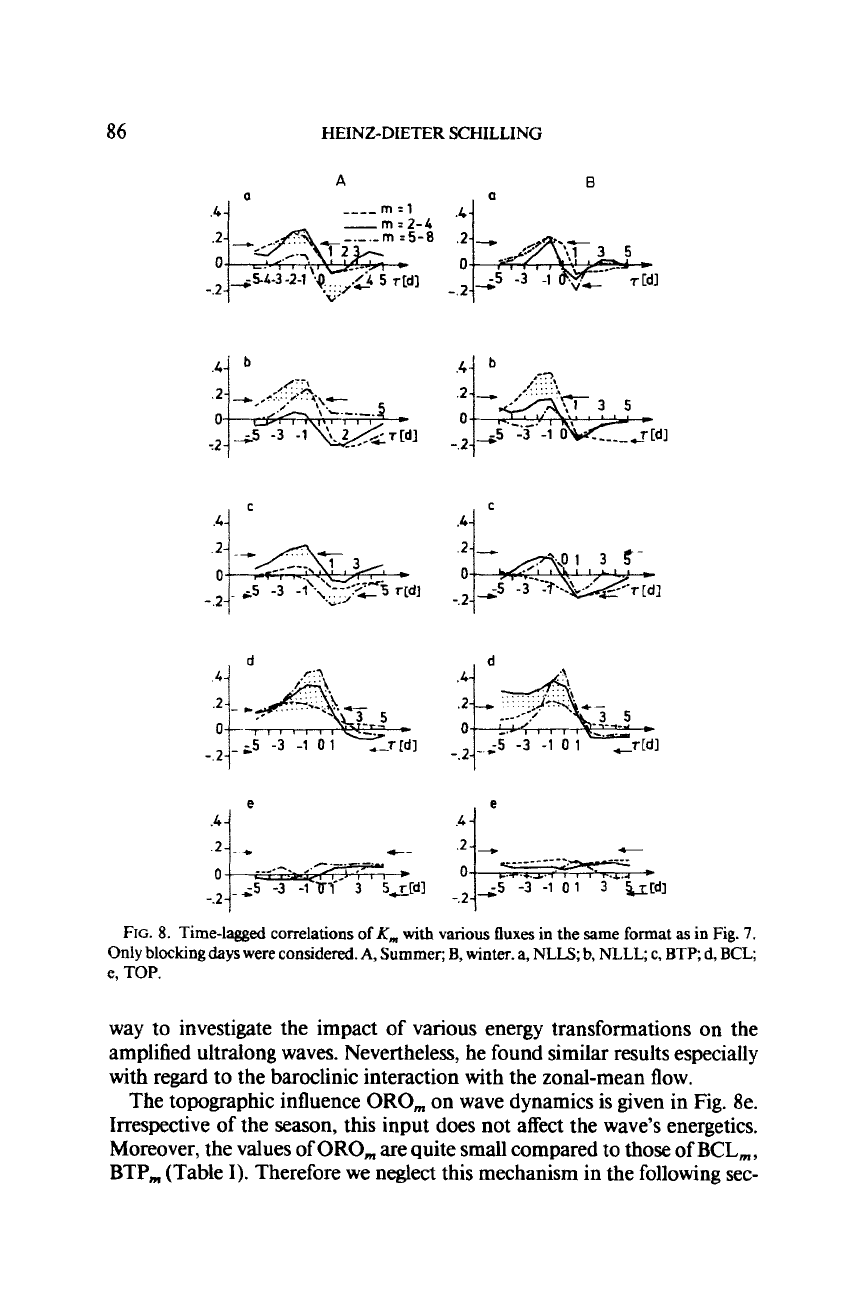
86

HEINZ-DIETER SCHILLING

FIG.

8.

Time-lagged

correlations

of

K,,,

with

various

fluxes

in

the

same

format

as

in Fig.

7.

Only

blocking

days

were

considered.

A,

Summer;

B,

winter.

a,

NLLS;

b,

NLLL;

c,

BTP;

d,

BCL;

e,

TOP.

way to investigate the impact of various energy transformations on the

amplified ultralong waves. Nevertheless, he found similar results especially

with regard to the barwlinic interaction with the zonal-mean flow.

The topographic influence

ORO,

on

wave dynamics is given in Fig. 8e.

Irrespective of the season,

this

input does not affect the wave’s energetics.

Moreover, the values of

ORO,

are quite small compared to

those

of BCL,,

BTP, (Table

I).

Therefore we neglect this mechanism in the following sec-

ON ATMOSPHERIC BLOCKING TYPES AND NUMBERS

87

TABLE

I.

SEASONAL AVERAGES

OF

SEVERAL ENERGY FLUXES~

Season

BTP,-, BTP,-, BCL1-, BCLS-, ORO,-,

0ROs-(

NLU1-4

NLU5-,

Dec-Feb

-0.331 -0.104 1.861 0.417 0.021 0.007 0.177 -0.206

Mar-

May

-0.083

-0.102

1.244 0.576 0.007 0.013 0.156 -0.246

Jun-

Aug

-0.119 -0.186 0.606 0.459 0.001 0.009 0.040 -0.083

Sep-

Nov

-0.336 -0.315 1.712 0.758 0.021 0.006 0.090 -0.187

Averages

are

for

the ultralong wavegroup (index

1

-4)

and the “synoptic” wavegroup (index

5

-

8).

For

definitions

of

the fluxes see text.

Units

are

W

m-*.

tions. This is not to

say

that it may be completely irrelevant, e.g., it can

provide for a triggering mechanism.

The next effect, the input from smaller scales by nonlinear interaction

NLLS, (Fig. 8a) shows a significant signal for the blocking wavegroup

m

=

2 -4

in summer and winter.

The last flux NLLL,, measuring the interaction within the long wave

packet, is shown in Fig. 8b. It seems to have little effect on

m

=

2-4

in

summer, but a stronger effect in winter. Except for

m

=

1,

the impact of this

term on the wave dynamics in a long-term sense is not quite clear.

5.2.

Regression

Analysis

There is another way to demonstrate the ability of these energy conver-

sions to build up the long waves kinetic energy. To this end we use a regres-

sion model derived from the tendency equation of

K,

[Eq.

(7)] in the rele-

vant latitude belt. Using an idea of

Y.

Hayashi (personal communication,

1985), we derive the model from the original equation in two steps. First we

fit the (artificial) damping constants

k,

to the reduced energy tendency after

(17)

(d/dt)K,

-

BTP,

-

BCL,

-

NLLS,

-

NLLL,

-

ORO,

=

Yo

=

-

k,K,

+

residue

This is done for

m

=

1

and for the wavegroups

m

=

2-4

and

m

=

5

-8.

The lag-

1

-day

autocorrelation of BOUND, is about 0.12 and is low com-

pared to the same correlation for BCL, (about

0.5

--*

0.8) or for

K,

(about

0.7). Thisjustifies our assumption that the boundary term BOUND,is noisy

and can be included in the residue. The (artificial) damping

k,

is in the order

of

-f

day. Secondly, having the maximum likelihood estimate of

k,

from Eq.

88

HEINZDIETER SCHILLING

(17), we turn over to the model

(d/dt)Km

+

k,K,

=

a,BTP,

+

azBCL,

+

CU~NLLS,

a4NLLL,

+

ar,ORO,

+

residue

=

Y

+

residue (18)

Retaining only some regression coefficients

ai

and setting the other to zero

gives a hierarchy of nested more and more complicated models

Y.

The

‘‘skill”

SKILL2

of those truncated models is given by

VAR(

Y)

VAR(dK,/dt

+

K,K,,,)

SKILL2

=

(19)

where

VAR

denotes variance. One hierarchy

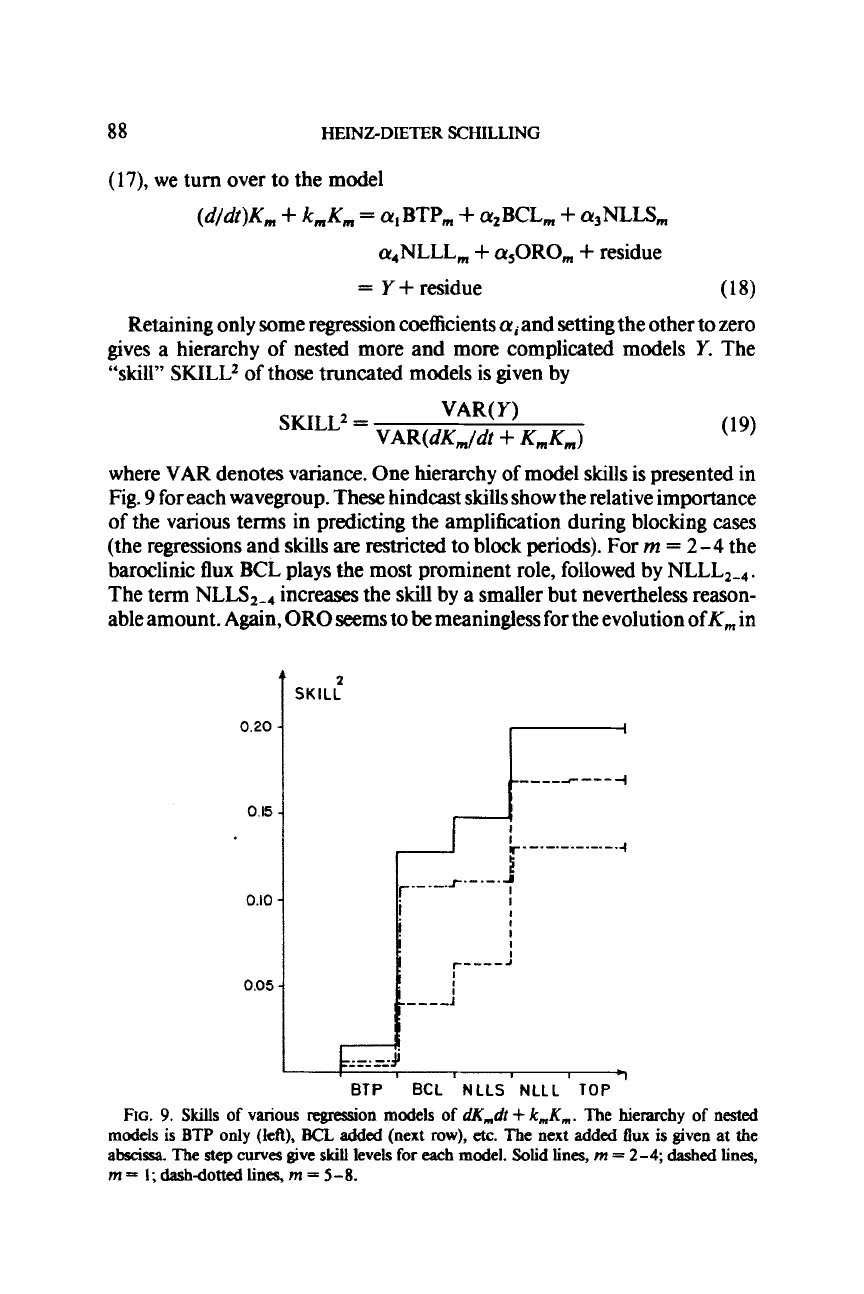
of

model skills is presented in

Fig.

9

for each wavegroup. These hindcast skills show the relative importance

of the various terms in predicting the amplification during blocking cases

(the regressions and

skills

are

restricted to block

periods).

For

rn

=

2-4

the

baroclinic flux

BCL

plays the most prominent role, followed by

NLLL,-,

.

The term

NLLS2-4

increases the

skill

by

a

smaller but nevertheless reason-

able amount.

Again,

OR0

seems to

be

meaningless for the evolution ofK, in

2

1

SKILL

0.20

0.6

0.10

0.05

FIG.

9.

Skills

of

various

regression models

of

dKmdt

+

k,K,.

The hierarchy

of

nested

models

is

BTP

only (left),

BCL

added

(next

row),

etc.

The

flux

is

given at the

abscissa.

The

step

curves

give

skill

levels

for

each

model.

Solid

lines,

m

=

2-4;

dashed

lines,

m

-

I;

dashdotted

lines,

m

=

5-8.

ON

ATMOSPHERIC BLOCKING TYPES AND NUMBERS

89

all cases. Similar results hold for

m

=

5

-

8,

but the skill of the most compli-

cated model

Y

is somewhat smaller in these

cases.

For

m=

1

the skill

contribution of NLLL, is much larger than that of BCL, in contrast to the

other wavegroups. Since these regression models were intended to show

previous results from another point of view, there is no need to analyze their

significance in this case.

We end this section with the conclusion that

OR0

can

be

discarded

in the

following analysis. Moreover, to make things simpler we deal with the com-

bined

flux

BTP

+

fiom now on. In

this

term BTP and NLLL are added for

each wavegroup before it is normalized after

Eq.

(1

5).

Therefore BTP

+

is

comparable to the other fluxes.

6. TYPES

OF

BLOCKING

It

is

of value to separate blocking

cases

into various types. We are aware of

the fact that the energy conversions can cooperate or compete and are

interested in whether certain patterns of cooperation are preferred by the

fluxes or not. Here we show that the cooperation patterns ofthe energy fluxes

associated with the dominant wave are helpful for our goal of rational classi-

fication of cases.

As a simplification we establish the dominant wave (group) for each

blocking case. To this end we

use

the following approach. First we average

the normalized fluxes BTP

+,

,

BCL,

,

and

NLLS,

for each case separately.

Since often energetics has inhomogenous characteristics during longer

pe-

riods, we have split up blocks with

a

duration longer than

15

days into two

halves. Those segments

are

treated

as

separate cases in

this

context. The

triplet of averaged fluxes together with the averaged kinetic energy stand for

the energetics of a wave/wavegroup in each

case.

Second, we establish a regression model for

dK,/dt

similar to

Eq.

(

18)

but

with BTP

+

instead of BTP and NLLL and neglecting

ORO.

With this model

we obtain an estimate for

K,

by an Euler backward approximation (At

=

1

day):

K,,,(t)

=

exp(-k,Af)

-

K,(f

-

At)

+

At

exp(-k,At/2)

(20)

This formula can be regarded

as

being

a

score with weighted inputs

K,,

BCL,

,

BTP

+,

,

and NLLS,

.

Since its form

is

conserved if averaged over a

case,

we simply consider the wave/wavegroup with maximum averaged

score

K,

to be dominant.

Accordingly, we can split up the total of 222

cases

into three subsets with

*

[aiBTP+,

(t)

+

aZBCL,(t)

+

CV~NLLS,(~)]

90

HEINZ-DIETER SCHILLING

dominant

m

=

1

(30%

of

cases),

m

=

2-4

(48%),

and

m

=

5-8

(22%).

The dominant wave/wavegroup is an additional entry of the catalog

of

Appendix C.

The cooperation of the energy inputs is studied for each subset separately

by means

of

an empirical orthogonal function

(EOF)

analysis. The

EOFs

are

shown in Fig.

10.

They are all significant to at least the

95%

level as revealed

by a Monte Carlo experiment with

3000

outcomes. In this test the computa-

tion of eigenvalues

was

repeated after interchanging fluxes of the same kind

randomly between cases, thereby destroying the cooperation patterns. The

test variable

was

the sum of absolute eigenvalue deviations from the trivial

ones

(=

autocovariances

of

the fluxes).

The

EOFl

explains about half

of

the variance and has approximately the

1

0

*I*

€Of

1

EOf

2

EOF

3

FIG.

10.

EOFs

of

the triplet

(NLLS,,

BCL,,,,

BTPi-,);

subscript

m

stands

for

three

wave

group subsets:

m

=

1,

m

=

2-4,

and

m

=

5-8.

ON

ATMOSPHERIC

BLOCKING TYPES

AND

NUMBERS

91

same form for each subset. If taken positive, it describes a combined input by

BCL and NLLS, counteracted by BTP+. This EOF represents one of the

basic mechanisms for feeding in energy to the leading blocking wave. It bears

close resemblance to the process described by Reinhold and Pierrehumbert

(1982) (in their model, topography seems to be needed for fixing the long

wave’s phase only). The negative EOFl consists completely of barotropic

inputs, namely the interaction with

m

=

1

-

5 and the zonal flow. The term

BCL is then below normal (note that

all

these fluxes

are

standardized). The

negative EOFl is comparable to barotropic instability theory.

The next EOF2 explains about

33% of the variance and differs from subset

to subset with respect to the role of NLLS. Basically, if taken negatively, it

describes the cooperation of BCL and BTP+

as

inputs.

NLLS

acts against it

or is at least small. This second main pattern was reported earlier by Hansen

and Chen (1982) and Chen and Shukla (1983) in cases of dominant

m

=

2

-

4.

If nonlinear interaction within the long wave packet is the leading term in

BTP+, this EOF fits the model results of Schilling (1982) too. The same

pattern taken positive would fit barotropic models with the synoptic scale

input NLLS only

(J.

Egger,

W.

Metz, and

G.

Muller, this volume).

The third EOF explains about 20% of the variance and differs considerably

from subset to subset. The positive pattern describes the leading role of

NLLS alone

(m

=

2 -4) or together with BTP

+

(m

=

1,

m

=

5

-

8). Fischer

(1984) reported that a similar blocking mechanism prevailed in his

GCM

blocking cases.

If

taken negatively the EOF3 would lead to

a

dissipation of

blocking waves, except for

rn

=

2

-

4 where a small baroclinic input could

serve as an energy support.

Note that other blocking models like that by Charney and DeVore

(

1979)

or

Legras

and Ghil(1985)

fail

completely in finding an EOF counterpart.

This is because those models are mainly based on

a

strong input by

OR0

which generally

is

absent in real

cases.

Unfortunately many of our 222 cases can not be projected onto only one

pattern. Nature is much more complex. Nevertheless, we can find out the

pattern or combination of patterns which optimizes the projection of flux

vector

a

onto a subspace for each case. If all combinations with

n

patterns

failed to project at least 75% of the length of vector

a,

a next try was made

with

n

+

1 patterns. The procedure was terminated when this criterion was

first met. The resulting

n

patterns were set to be the governing pattern of the

case.

Since this procedure yields about 10 different combinations or more it

was decided to collect similar governing patterns in types. Additionally, all

cases with no single flux being larger than 0.25 were collected into a separate

class

named “no-type.”

Besides this no-type category we found another six

types

corresponding to

six certain EOF patterns, respectively. For example, type “BCL” is the set of

92

HEMZDIETER

SCHILLING

all

cases characterized by a positive EOFl,

or

its combination with another

EOF

which conserves the positive

EOFls

main features.

The resulting types and their characteristics

are

given in Table

11.

The

dominating ensemble- and type-averaged fluxes are relatively large. All

values except those in parentheses are significantly different from normal

(=

zero) at a

95%

level.

Types with NLLS input are more important for

rn

=

1

than for other

dominant wavegroups: their relative frequency

is

29%

(m

=

l),

22%

(rn

=

2

-4),

and

10%

for

rn

=

5

-

8.

Types with positive BCL were found in

43%

(rn

=

l),

43%

(rn

=

2-4),

and

56%

(rn

=

5-8) ofthe

cases.

Positive BTP+

was recorded in

37.5%

(rn

=

l),

38%

(rn

=

2-4),

and

44%

(rn

=

5-8)

ofthe

The type-averaged blocking number

Bl

is also shown in Table

11.

Circum-

polar types are found mainly in the

rn

=

2-4

subset.

As

expected,

B1

is

considerably smaller for the

rn

=

5

-

8 subset in general. Indeed, dominating

waves with

rn

=

5-8

should emphasize local structures. Therefore we

should define the lower bound of

Bl

related to circumpolar behavior in such

a way that most

cases

of the

rn

=

5-8

subset have smaller

Bl

values.

There is no general relation between

BI

and the dominant energy input.

On the other hand

BIis

somewhat smaller in the

cases

where BCL

is

the only

input. This is especially true for

rn

=

5-8

cases,

a result that may

be

a

consequence

of

the

Bl

dependence of baroclinic activity

as

discussed in

Section

4.

Such classifications of

cases

may

be

helpful in organizing

case

studies

invoIving historical

data.

Therefore we add the type for each block to the

catalog of Appendix C. The

cases

in that catalog are selected to

be

character-

ized by

BIZ

2.

Therefore the circumpolar averaged fluxes are especially

appropriate for our classification. We

are

aware of the fact that boundaries

between blocking

cases

will

be

always a bit artificial due to the complexity of

nature. Classification

will

be

more successfull the more the characterizing

parameter points

of

cases

tend

to build up separate clusters in parameter

space. We show now that

this

tendency

is

observable in the space spanned by

the fluxes BCL, BTP+, and

NLLS.

Each

case

is given

by

the point (BCL,

BTP+,

NLLS)

of averaged

fluxes.

Figure

1

la and b show BCL-BTP+

projections of this

space

for

two

different ranges of NLLS. All

cases

are taken

into account and we observe a relative large spread of points over the entire

plane. However, there

are

three clusters separated by relatively low point

density regions. Moreover, those clusters correspond roughly to different

types given above. Since the EOFs behind these types are significant at the

95%

level, it is presumed that these clusters are not artifacts of our sample.

As

to this point we made tests with flux averages over

periods

shifted forward

1

or

2

days

relative to the blacking period. Thereby we found that the clusters

cases.

TABLE

11.

CHARACTERISTICS

OF

TYPES

Type

None

BTP+

BCL/BTP+

NLLS/BTP+

NLLS

BCL

BCL/NLLS

NLLS

m=L m=2-4

-0.28

-0.09

-0.47 (-0.02)

-0.43 (0.02)

0.64 0.46

0.67

0.57

(0.12) (0.07)

0.50

0.57

m

=

5-8

BCL

m=l m=2-4 m

=

5-8 m=l

BTP+

m

=

2-4

m=5-8

~

(-0.02)

(-0.17)

-0.40

0.95

1.50

-

(-0.06)

(-0.15) -0.18

-0.78 -0.32

0.59 0.54

(0.03)

(-0.46)

0.64 0.72

1.02 0.43

(-0.20)

(0.06)

(-0.03)

-0.40

0.62

-0.17

0.90

0.59

-

(-0.08)

0.68

0.60

0.50

0.29

-0.52

(0.26)

-0.24

0.60

0.45

0.57

(0.09)

-0.57

-0.31

(-0.1

1)

0.62

0.41

-

(-0.49)

-0.34

-0.97

m=

1

1.22

1.56

1.47

1.52

1.24

1.33

1.83

BI

m-2-4 m=5-8

Relative

frequency

(%)

m=l m=2-4 m=5-8

~

1.67 1.18

1.90

1.25

1.93

1.11

1.72

-

1.91 1.45

1.41 0.92

1.30

1.09

21 23 21

I1

13

15

14 23 29

12.5 2

12.5 19 8

25 19 25

4

I

2

-

Saltzman B. (editor) Anomalous Atmospheric Flows and Blocking

Подождите немного. Документ загружается.