Рыков В.В., Иткин В.Ю. Математическая статистика и планирование эксперимента

Подождите немного. Документ загружается.

Глава 2 Точечное оценивание параметров 60

В с илу нераве нства Иенсена для с.в. η =

L(θ; x)

L(θ

; x)

имеем для θ 6= θ

ln η ≤ ln M

η = 0, (7.7)

так как

η = M

L(θ; x)

L(θ

; x)

p(x; θ)

p(x; θ

)

· p(x; θ

)dx = 1.

Таким образом, из неравенства (7.6) имеем в окрес тности локаль-

ного максимума

ln L(θ; x) ≤ M

ln L(θ

; x). (7.8)

Но ∀θ ∈ Θ

ln L(θ; x) =

1≤i≤n

ln p(x

, θ)

является нормированной суммой н.о.р. с.в. и по УЗБЧ сходится с

вероятностью 1 к своему математическому ожиданию

ln p(X; θ) = M

ln L(θ; x). (7.9)

Следовательно, из (7.8) и (7.9) для достаточно больших n имеем,

что с вероятностью 1 ∀θ 6= 0.

ln L(θ; x) ≤ ln L(θ

; x) (7.10)

Сравнивая (17.7) и (7.10) получаем, что при n → ∞ с вероятностью 1

l(θ; x) → l(θ

; x).

Откуда в случае непрерывности и взаимной однозначности функции

L по θ получим, что

{ lim

n→∞

(x) = θ

} = 1,

т.е. сходимость

к θ

с вероятностью 1,— утверждение более силь-

ное, ч ем состоятельность.

Строгое доказательство этой теоремы требует некоторых допол-

нительных условий регулярности. Его можно найти, например, в [7],

[12].

Глава 2 Точечное оценивание параметров 61

7.5 Асимптотические эффективность и нормальность

ОМП

Покажем, следуя Крамеру [12] (см. также [7] [?], с тр. 61-70), что

при выполнен ии некоторых условий регулярности ОМП асимптоти-

чески нормальна и эффективна.

Теорема 7.1. Пусть ф.п. имеет две производные по θ в окрестно-

сти U

истинного значения θ

параметра θ и пусть

(a)

∂l

∂θ



θ=θ

= 0;

(b)

(θ) = −M

∂

(∂θ)

= M



∂l

∂θ



6= 0, для θ ∈ U

Тогда ОМП θ асимптотически нормальна, т.е.

R(θ

)(

− θ

) → N(0, 1). (7.11)

Доказательство. Раскладывая производную по θ от логарифма

ф.п. в точке

в ряд Тейлора в окрестности U

истинного значения

параметра θ и учитывая, что

— ОМП име ем

θ =

∂ ln L

∂θ



∂ ln L

∂θ



+ (

− θ

)

∂

ln L

(∂θ)



∗

где θ

∗

заключено между θ

и θ

∗

. Откуда

(

− θ

)R(θ

) =

∂ ln L

∂θ



· R

−1

(θ

) +

∂

ln L

(∂θ)



∗

· R

−2

(θ

). (7.12)

В силу состоятельности оценки

θ (см. предыдущий раздел) по

УЗБЧ им еем с вероятностью 1



lim

n→∞

∂

ln L

(∂θ)



= M

∂

ln L

(∂θ)





= 1.

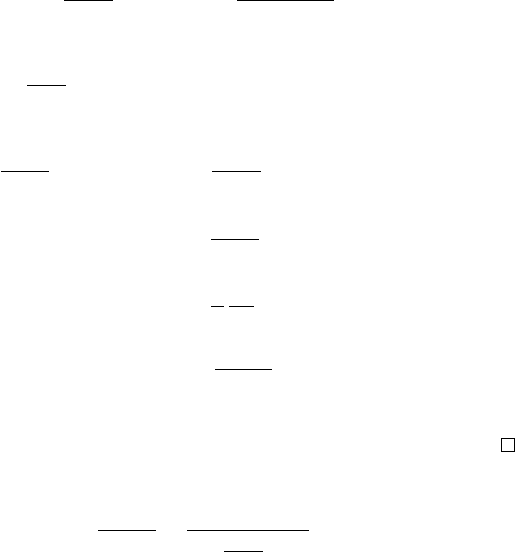
Глава 2 Точечное оценивание параметров 62

Откуда, т.к. θ

∗

заключено между θ

и θ

∗

, знаменатель в правой части

(7.12) сходится с вероятностью 1 к 1. Далее, т.к.



∂ ln L

∂θ





1≤i≤n

∂ ln p(x

; θ)

∂θ



является суммой n н.о.р. с.в. с м.о. равным в силу предположения

(а) нулю, M



∂ ln L

∂θ





= 0, и дисперсией, равной в силу предполо-

жения (b)



∂ ln L

∂θ







= M



∂ ln L

∂θ







∂ ln L

∂θ





· p(x; θ

) dx =



∂L

∂θ





· p(x; θ

) dx =

= −M

∂

ln L

(∂θ)

= R

(θ

то числ ител ь, а вместе с ним и величина (

− θ

)R(θ

) с вероятно-

стью 1 сходится к стандартной нормальной с.в. N(0, 1).

Следствие. Так как

(θ

)



∂ ln L

∂θ





является минимальной границей для любой функции от оценки в

неравенстве Рао-Крамера, то ОМП

- асимптотически эффек-

тивна.

7.6 Дополнения

Вопросы для контроля

1. Дайте опр еде лен ия:

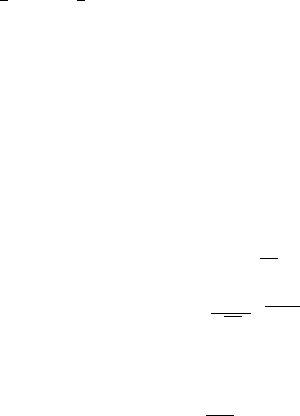
Глава 2 Точечное оценивание параметров 63

a) функции правдоподобия,

б) оценки максимального правдоподобия.

2. Как связаны эффективные оцен ки и ОМП?

3. Как связаны ОМП с достаточными статистиками?

4. Сформулируйте условия, при которых ОМП состоятельна и

асимптотически нормальна.

Упражнения

1. Пусть вероятность успеха в схеме Бернулли м ожет принимать

лишь два значения, p

, p

. Найти ОМП.

2. Рассмотреть эту же задачу в предположении, что параметр p

принимает произвольные значения в отрезке [0, 1].

3. Вычислить ОМП для параметров нормального распределения

N(θ

, θ

4. Найти ОМП дл я равномерного распределения на отрезках: (а)

[0, θ]; (б) [θ

, θ

5. Вычислить ОМП для пар аметр ов

• геометрического распределения: Geo

(p) = (1 − p)p

, k =

0, 1, 2 . . . ;

• пуассоновского распределения: Poi

(λ) =

−λ

, k =

0, 1, 2 . . . ;

• нормального распределения: p(x; µ, σ

) =

√

2π σ

x−µ

2σ

;

• показательного распределения: p(x, λ) = λe

−λ

{x≥0}

;

• показательного распределения со сдвигом: p(x; λ, a) =

λe

−λ(x−a)

x≥a

;

• равномерного распределения: p(x; a, b) =

b−a

{a≤x≤b}

Глава 3.

ТЕОРИЯ ИНТЕРВАЛЬНОГО

ОЦЕНИВАНИЯ И НЕКОТОРЫЕ

РАСПРЕДЕЛЕНИЯ

МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

§ 8 Постановка задачи

8.1 Вводные замечания

Теория точечного оценивания параметров, рассмотренная в

предыдущей главе, позволяет строить оценки

θ неизвестных пара-

метров θ в виде функций

θ = T (x

, x

, . . . , x

) от выборочных (на-

блюдаемых) значений x = (x

, x

, . . . , x

). При этом нужно отдавать

себе отчет в том, что даже наилучшие оценки (НОМД) поз воляют

оценивать неизвестные параметры лишь “в среднем”, т.е. в качестве

оценок получать с.в.

θ = T (X), которые лишь в среднем группи-

руются около оцениваемого параметра (если оценка несмещенная

θ = θ) и лишь с ростом n по вероятности сходится к оценивае-

мому параметру (если оценка состоятельна lim

n→∞

(p)

= θ). Мерой

отклонения оценки от истинного значения параметра является дис-

персия D

θ, которая, вообще говоря, также неизвестна и может быть

приближенно заменена эмпирической дисперсией оценки.

Естественно возникает вопрос о надежности (достоверности) оце-

нок и не асимптотически (пр и больших n), а при конкретных фикси-

рованных значениях объема выборки n. Для решения этого вопроса

Дж. Нейман (1937) предложил теорию интервального оценивания,

сущность которой состоит в следующем.

Пусть

θ = T (X) - оценка параметра θ. Тогда, т.к.

θ является с.в.

над семейством выборочных пространств (X, P = P

), она имеет

некоторое распределение

(t; θ) = P

{

< t},

вообще г оворя также зависящее от параметра θ.

Глава 3 Интервальное оценивание параметров 65

Однако, если удастся построить функцию от выборки g = g(x; θ),

распределение которой не зависит от θ, т.е.

{g(X; θ) < t} = F (t) при любых θ ∈ Θ,

то с помощью этого распределения можно делать так называемые

доверительные утверждения, а именно: выберем числа α

, α

(0 <

< 0.5) и найдем g

, g

так, чтобы выполнялись неравенства

F (g

) ≤ α

, F (g

) ≥ 1 − α

. (8.1)

Тогда полагая α

+ α

= α имеем для любого θ ∈ Θ,

< g(x; θ) ≤ g

} = F (g

) − F (g

) ≥ 1 − α

− α

= 1 − α, (8.2)

т.е. с вероятностью не меньшей, чем 1 − α справедливо неравенство

< g(x; θ) ≤ g

. (8.3)

Далее, если функция g(x; θ) монотонна, по второму аргументу,

то используя обратную функцию θ = g

(−1)

(g, x) = t(g, x) и решая

неравенство (8.3), получи м нер авенство

(x) = t(g

, x) < θ ≤ t(g

, x) = t

(x), (8.4)

которое при всех θ ∈ Θ выполняется с вероятностью не меньшей,

чем 1 − α.

Замечание. Здесь параметр θ не является случайной величиной.

Случайны (от выборки к выборке) концы интервала t

(x) и t

(x),

и утверждение (8.4) следует понимать в том смысле, что с вероят-

ностью не меньшей, че м 1 − α случайный интер вал (t

(x), t

(x)] на-

крывает неслучайное значение параметра θ. Другими словами , если

пронаблюдать N независимых выборок x

= (x

, . . . , x

), . . . , x

, . . . , x

), то в среднем в (1−α)N случаях неизвестное значение

параметра θ окажется внутри интервала (t

(x), t

(x)], и лишь в αN

случаях вне его.

Глава 3 Интервальное оценивание параметров 66

8.2 Определения

Определение 8.1. Вероятность 1 −α, с которой выполняется соот-

ношение (8.4) п ри всех θ называется доверительной вероятностью,

или коэффициентом доверия.

Определение 8.2. Функции t

(x) и t

(x), для которых соотноше-

ние (8.4) выполняется для всех θ ∈ Θ с заданными вероятностями α

и 1 −α

называются нижней и верхней доверительными границами

уровней α

и 1 − α

соответственно. Интервал (t

(x), t

(x)] называ-

ется доверительным интервалом с коэффициентом доверия 1 − α.

Определение 8.3. Объединение доверительных интервалов по все-

возможным выборкам, т.е. множество S = {(θ, x)} ⊂ Θ × X

, для

которого

(S) ≥ 1 − α

для всех θ ∈ Θ, называется доверительной областью.

8.3 Пример: X ∈ N (µ, 1)

Пусть с.в. X имеет нормальное распределение с неизвестным ма-

тематическим ожиданием µ и дисперсией σ

= 1. Чтобы по выборке

x = (x

, . . . , x

) построить доверите льный интервал для µ, заметим,

что с.в. ˆµ =

имеет нормальное распределение с параметрами

µ и

; стало быть (

X − µ)

√

n имеет стандартное нормальное рас-

пределение, (

X − µ)

√

n ∈ N(0, 1). Таким образом, выбирая в каче-

стве нижней и верхней доверительных границ соответствующие α

и 1−α

-квантили стандартного нормального распределения, т.е. зна-

чения c

, c

такие, что Φ(c

) = α

, Φ(c

) = 1 − α

получим

P{c

≤ (

X − µ)

√

n < c

} = Φ(c

) − Φ(c

) = 1 − α

− α

Откуда решая неравенство в скобках левой части найдем довери-

тельный интервал для µ с коэффициентом доверия 1−α = 1−α

−α

в вид е

(x) = ¯x −

√

< µ ≤ ¯x −

√

= t

(x).

Напомним двойственное отношение к выборке в статистике(см. замечание на

стр.16)

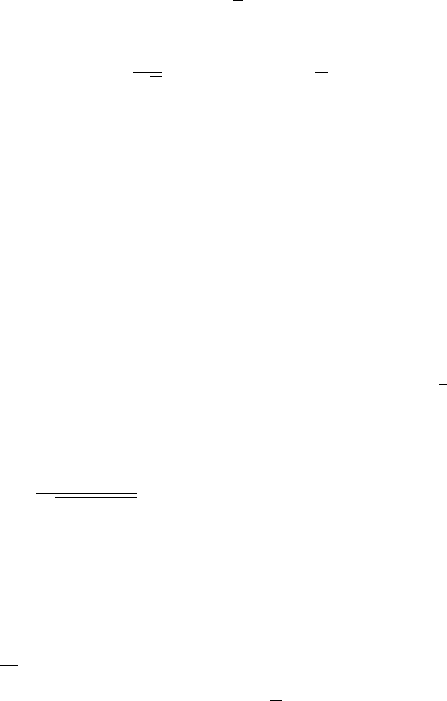
Глава 3 Интервальное оценивание параметров 67

В силу симметрии нормального распределения наименьшим бу-

дет интервал, для которого α

= α

. В этом случае c

= −c

доверительные границы принимают вид

(x) = ¯x ∓

√

, Φ(c) = 1 −

8.4 Доверительный интервал для неизвестной вероят-

ности в схеме Бернулли

Для построения доверительного интервала для неизвестной ве-

роятности p успеха в схеме Бернулли заметим, что число успехов ν

при n испытаниях имеет биномиальное распределение,

{ν

= k} = b

(n, p) =





(1 − p)

n−k

которое при соответствующей нормировке при n → ∞ очень быстро

сходится к стандартному нормальному. Например, при p =

уже

при n = 3 это приближение очень хорошее. Поэтому в силу симмет-

рии нормального распределения можно положить

(



− np

np(1 − p)



≤ c

)

= 2Φ(c) − 1 = 1 − α

и найдя по заданному α величину c построить доверительную об-

ласть из с оотношен ия

(ν

− np)

≤ c

np(1 − p)

или для h

− p)

≤ c

p(1 − p)

. (8.5)

Множество точек (h

, p), удовлетворяющих неравенству (8.5) ле-

жит внутри э лли пс а.

Глава 3 Интервальное оценивание параметров 68

Таким образом, для любого наблюденного значения частоты h

можно получить соответствующий доверительный интервал для p,

длина которого тем меньше, чем больше n. Из уравнения

− p)

= c

p(1 − p)

найдем значения доверите льных границ для p в зависимости от на-

блюденной частоты h

1,2

) =

∓

√

(1 − h

) +

1 +

Глава 3 Интервальное оценивание параметров 69

и длину интервала

∆ = t

) − t

) =

√

(1 − h

) +

1 +

подтверждающие высказанные суждения.

Замечание. Можно вычислить также точные доверительные гра-

ницы пользуясь биномиальным распределением.

8.5 Дополнения

Вопросы для контроля

1. Почему н еобходима оценка точности и достоверности статисти-

ческого оценивания параметров распределений?

2. В че м состоит сущность доверител ьного оцени вания?

3. Дайте опр еде лен ия:

а) доверительной вероятности;

б) верхней и нижней доверительных границ;

в) доверительного интервала;

г) доверительной области.

4. Как построить доверительный интервал д ля неизвестного ма-

тематического ожидания нормального распределения при известной

дисперсии?

5. Как построить доверительный интервал для неизвестного пара-

метра в схеме Бернулли?

а) с п омощью нормальн ой аппроксимации;

б) точный, с пом ощью биномиал ьного распре де лен ия.

Упражнения

добавить упр