Рыков В.В., Иткин В.Ю. Математическая статистика и планирование эксперимента

Подождите немного. Документ загружается.

Приложение A. Обработка данных на компьютере 180

0.2

0.4

0.6

0.8

1.2

1.5 2 2.5 3 3.5 4

Поле наблюдений рисует функция ScatterPlot. Она также поз-

воляет подобрать линию зависимости одной выборки от другой ме-

тодом наименьших квадратов. Для этого следует указать опцию

fit=[<формула>, <переменная>].

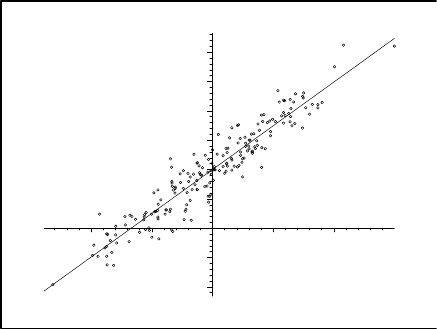
Пример 24.8. Рассмотрим две нормальных с.в.: X ∈ N(0, 1) и

Y = 4 + 3 X + ε, где ε ∈ N (0, 1).

> N := 200: # Объем выборки

> X := Sample(Normal(0, 1), N):

> Epsilon := Sample(Normal(0, 1), N):

> ONE:=Vector[row](N, 1): # Единичный вектор [1,1,..., 1]

> Y:=4*ONE + 3*X + Epsilon:

> # a, b - параметры, x - переменная

> ScatterPlot(X, Y, fit=[a*x+b, x]);

Приложение A. Обработка данных на компьютере 181

–4

–2

–2 –1 1 2

§ 25 Выборочные моменты

Для вычисления выборочных моментов применяются те же

функции, что и для получения моментов теоретических, н о первым

аргументом должна быть не с.в (типа RandomVariable), а выбор-

ка (типа Vector). Перечислим эти функции: Moment (начальный мо-

мент), CentralMoment (центральный момент), Mean (математическое

ожидание), Variance (диспе рси я), StandardDeviation (стандартное

отклонение), Variation (коэффициент вариации), Skewness (асим-

метрия), Kurtosis (эксцесс).

Напомним, что как наблюдения, так и функции от них (стати-

стики) можно рассматривать с двух точек зрения. До проведения

эксперимента они являются случайными величинами, после – реали-

зациями с.в., т.е. числами . Выборочные моменты – не исключение.

Рассматривая их как с.в., мы должны знать закон распределения.

В силу ЦПТ все выборочные моменты имеют асимптотически

нормальное распределение. Мат. ожидание равно теоретическому

значению каждого момента (по край ней мере асимптотически). Дис-

персия вычисляется для каждого момента в соответствии с распре-

делением исходной с.в. Для ее вычисления, а точнее, для вычисления

стандартного отклонения выборочных характеристик используется

Приложение A. Обработка данных на компьютере 182

функция StandardError.

Пример 25.1. Рассмотрим нормальную с.в., получим для не е вы-

борку и найдем выборочные моменты и их стандартные отклонения.

> # С.в. с неопределенными параметрами

> # для получения формул

> X0:=RandomVariable(Normal(mu, sigma)):

> # С.в. для числовых результатов

> X:=RandomVariable(Normal(2, 4)):

> n_:=1000:# Объем выборки

> x:=Sample(X, n_): # Выборка

Найдем выборочное мат. ожидание.

> Mean(X0); # Формула

> Mean(X); # Теор. значение

> Mean(x); # Выборочный момент

2.071028581

И его стандартное отклонение :

> StandardError[n](Mean, X0);# n - объем выборки

> StandardError(Mean, x);

0.1269865695

Найдем выборочную дисперсию.

> Variance(X0); # Формула

> Variance(X); # Теор. значение

> Variance(x); # Оценка дисперсии

> CentralMoment(x, 2); # Выборочный момент

Приложение A. Обработка данных на компьютере 183

16.12558884

16.10946325

Обратите вни мани е, что оценка дисперсии функцией Variance не

совпадает с результатом функции CentralMoment. Это связано с тем,

что CentralMoment(x, 2 ) вычисляется по формуле

i=1

− ¯x)

а Variance(x) – по

n − 1

i=1

− ¯x)

В этом случае оценка дисперсии оказывается несмещенной, т.е. ее

мат. ожидание совпадает с теоретической диспе рс ией (см. 4). Цен-

тральные выборочные моменты оказываются смещенными оценка-

ми, но смещение стремится к нулю с ростом объема выборки, поэто-

му и х можно считать асимптотически несмещенными.

Найдем отклонение выборочной дисперсии:

> StandardError[n](Variance, X0);

> StandardError(Variance, x);

√

2 σ

0.7050251112

Начальный момент третьей степени:

> Moment(X0, 3); # Формула

> Moment(X, 3); # Теор. значение

> Moment(x, 3); # Выборочный момент

3 σ

+ µ

104

107.4829654

Отклонение начального момента третьей степени:

Приложение A. Обработка данных на компьютере 184

> StandardError[n](Moment, X0, 3);

> StandardError(Moment, x, 3);

15 σ

+ 45 σ

+ 15 σ

+ µ

−



3 σ

µ + µ



9.914710634

Найдем центральный четвертый момент.

> CentralMoment(X0, 4); # Формула

> CentralMoment(X, 4); # Теор. значение

> CentralMoment(x, 4); # Выборочный момент

3 σ

768

756.5752136

Найдем его стандартное отклонение.

> StandardError[n](CentralMoment, X0, 4);

> StandardError(CentralMoment, x, 4);

√

6 σ

69.93981571

При исследовании выборок бывает полезно оценить нормирован-

ные моменты и сравнить их с теоретическими значениями для пред-

полагаемого распределения. Перечислим их:

• коэффициент вариации (Variation):

V =

;

• асимметрия (Skewness):

S =

;

• эксцесс (Kurtosis):

K =

Приложение A. Обработка данных на компьютере 185

Вычислим выборочный коэффициент вариации:

> Variation(X0);

> Variation(X);

> Variation(x);

1.938002990

Его отклонение:

> StandardError[n](Variation, X0);

> StandardError(Variation, x);

+σ

nµ

0.1336824948

Асимметрия и эксцесс для нормального распределения не зависят

от пар аметр ов µ и σ. Найдем асимметрию:

> Skewness(X0);

> Skewness(x);

−0.02302483916

Ее отклонение:

> StandardError[n](Skewness, X0);

> StandardError(Skewness, x);

√

0.07960635914

Эксцесс:

> Kurtosis(X0);

> Kurtosis(x);

Приложение A. Обработка данных на компьютере 186

2.912429734

Его отклонение:

> StandardError[n](Kurtosis, X0);

> StandardError(Kurtosis, x);

√

0.1577420320

Для смешанных моментов можно вычислить лишь выборочные

оценки.

Пример 25.2. Рассмотрим с.в. Y = 3.5X + ε, где ε ∈ N(0, 10). Най-

дем ковариацию и коэффициент корреляции для выборок y и x из

предыдущего примера .

> eps:=Sample(Normal(0, 10), n_):

> y:=3.5*x+eps:

> Covariance(x, y);

54.71583328

> Correlation(x, y);

0.8048266525

Чтобы найти моменты по сгруппированной выборке, следует ис -

пользовать п акет stats – в пакете Statistics для этого нет средств.

Пример 25.3. Загрузим пакет stats и его подпакеты.

> with(stats): with(describe):with(transform):

> # Преобразуем выборку в список

> x_:=convert(x, list):

> # Зададим интервалы группировки

> ranges := [-11 .. -8.3, -8.3 .. -5.6, -5.6 .. -2.9,

> -2.9 .. 0, 0 .. 3, 3 .. 5, 5 .. 8, 8 .. 11,

> 11 .. 13, 13 .. 16]:

> # Сгруппируем выборку

> g:=tallyinto(x_, ranges);

Приложение A. Обработка данных на компьютере 187

g := [W eight(−11.. − 8.3, 5), W eight(−8.3.. − 5.6, 20),

W eight(−5.6.. − 2.9, 84), W eight(−2.9..0, 197), W eight(0..3, 277),

W eight(3..5, 178), W eight(5..8, 180), W eight(8..11, 40), W eight(11..13, 17),

W eight(13...16, 2)]

Найдем выборочные моменты двумя способами: по исходной и по

сгруппированной выборкам.

> # Мат. ожидание

> mean(x_); mean(g);

2.071028586

2.080600000

> # Дисперсия

> variance(x_); variance(g);

16.10946327

16.58895864

Функция moment имеет три параметра в квадратных скобках и

аргумент-выборку в круглых. Параметр p – порядок момента, два

других параметра необязательны: центр c и количество ограничений

moment[p, c, k](x) =

n − k

i=1

− c)

Если c не зависит от выборки (например, 0 для начального мо-

мента или теоретическое мат. ожидание для центрального), то сле-

дует задать k = 0. Если же c вычисляется по выборке (например,

выборочное мат. ожидание), то для получения несмещенной оценки

следует положить k = 1. Это имеет смысл только для исходной вы-

борки, поскольку для сгруппированной оценка в любом сл учае будет

смещенной.

> # Третий начальный момент

> moment[3](x_); moment[3](g);

107.4829653

113.2715253

Приложение A. Обработка данных на компьютере 188

> # Четвертый центральный момент

> moment[4, mean(x_)](x_); moment[4, mean(g)](g);

756.5752143

797.7023707

Приложение B.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ

РАБОТЫ

Приводимые ниже статистические данные содержат различную

геологическую, промысловую и пр. информацию.

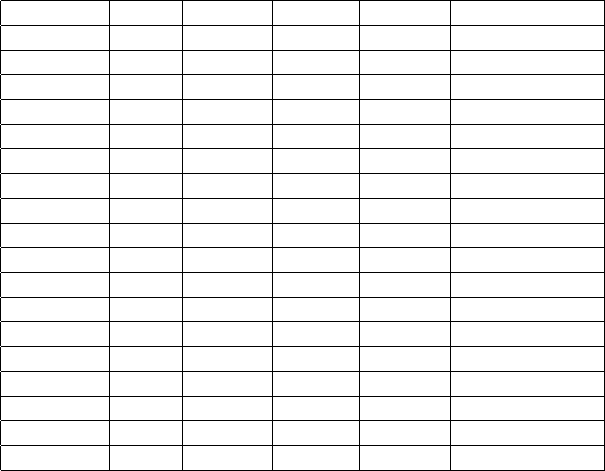
Задание 1.

В результате промыслово-геофизических исследований и экспери-

ментов на кернах были получены следующие выборки фактиче-

ских значений геол ого-физи чес ких параметров залежей Балахны-

Сабунчи-Романы, пр ивед енн ые в таблице 1, где S

гл

– глинистость,

пес

– песчанистость, K

пор

– пористость, K

пр

- проницаемость,

кар

– карбонатность.

Таблица 1.

№ п.п . S

гл

% K

кар

% K

пес

% K

пор

% K

пр

∗ 10

−15

1 22 12 81 25 36

2 29 13,2 66 24,7 160

3 27 12 54 26,2 197

4 22 7 76 25,8 378

5 31,5 13 52 25,8 154

6 23,0 11 81 25,8 364

7 25,0 11 48 26.9 167

8 18 10 74 25,9 132

9 29 9 28 22,6 90

10 22 10 80 24,4 374

11 34 12 51 25,1 94

12 33 13 50 24,9 94

13 35,6 13 51 24,8 90

14 32 13 54 24,4 96

15 34 19 55 25,0 89

16 33 13 52 24,3 90

17 39 13 82 23,8 340

18 26 13 85 22,4 303

Для всех пяти указанных параметров: