Рыков В.В., Иткин В.Ю. Математическая статистика и планирование эксперимента
Подождите немного. Документ загружается.


Глава 5 Планирование эксперимента 140
§ 20 Планирование многомерного эксперимен-
та
Вообще говоря, вся статистика занимается планированием экс-
перимента в широком смысле этого слова, так как для получения
желаемых результатов необходимо выбрать количество опытов обес-
печивающих заданную точность оценки параметров, или оценить
точность полученных результатов по имеющимся наблюдениям, и
решение этих вопросов можно рассматривать как решение вопро-
сов, относящихся к планированию эксперимента. Однако, в стати-
стике под планированием эксперимента принято понимать довольно
узкую область, связанную с планированием многомерного экспери-
мента, которая и будет рассмотрена в настоящем разделе.
20.1 Постановка задачи. Основные понятия
Одной из наиболее важных и распространенных задач многомер-
ного статистического анализа является задача оценки коэффициен-
тов β
j
линейной регрессионной модели
y = β
0
+ β
1
φ
1
(x
1
, . . . x
k
) + . . . β
r
φ
r
(x
1
, . . . , x
k
) (20.1)
и изучения их свойств. При этом предполагается, что неизвестные
параметры входят в выражение (20.1) линейно, а сами независимые
(регрессионные) переменные x
j
, j =
1, k, вообще говоря, не обяза-
тельно линейно, а в виде некоторых известных функциональных
зависимостей φ
j
(x
1
, . . . , x
k
), j = 1, r. В простейшем случае наблю-
даемая величина связана с регрессионными переменными (которые
могут быть, вообще говоря, статистически зависимыми) также ли-
нейной зависимостью
y = β
0
+ β
1
x
1
+ . . . β
k
x
k
. (20.2)
Предполагается, к роме того, что при наблюдениях возникают слу-
чайные ошибки, так что вместо y наблюдается с.в. Y ,
Y = β
0
+ β
1
x
1
+ . . . β
k
x
k
+ , (20.3)
Глава 5 Планирование эксперимента 141
причем ошибки наблюдений в различных опытах независимы и оди-
наково нормально распределены, ∈ N(0, σ
2
).
Здесь независимые переменные называются регрессионными, или
фа кторными перем ен ным и, ил и просто фа кторами, а множество
их допустимых значений факторным пространством. Зависимость
(20.1) часто называют функцией отклика, а геометрическое место
точек, отвечающее этой зависимости,—поверхностью отклика. Вид
поверхности отклика для случая двухфакторной модели представ-
лен на рис.1.
Здесь заштрихованный в плоскости x
1
0x
2
прямоугольник пред-
ставляет собой факторное пространство. Если величины x
1
, . . . , x
k
также недоступны точному измерению, т.е. являются случайными
величинами, то вопросы анализа зависимостей (20.1, 20.2) реша-
ются обычно в рамках корреляционной теории. Если же величины
x
1
, . . . , x
k
не случайны, т.е. могут быть фиксированы и измерены
точно, то соответствующие вопросы решаются методами регрессион-
ного или дисперсионного анализов. При этом, если переменные (фак-

Глава 5 Планирование эксперимента 142
торы) изменяются непрерывно в некоторой области, используются
методы р егр есс ионн ого анализа. При необходимости исследования
зависимостей (20.1, 20.2) по качественному пр из наку, когда факто-
ры принимают лишь два значения: наличие x
j
= 1 или отсутствие
x
j
= 0 влияния j-го фактора на наблюдаемую величину y, исполь-
зуются методы дисперсионного анализа.
Если регресс ионн ые переменные не случайны, то проводя незави-
симые эксперименты в различных точках факторного пространства
X, будем получать в качестве наблюдений y
i
, i = 1, n реализации
н.о.р. с.в. Y
i
, i = 1, n.
Матрица X = [x
ij
]
1≤i≤n, 1≤j≤k
, составленная из координат точек
x
ij
проведения экспериментов, называется матрицей плана экспе-
римента (МПЭ),
X = [x
ij
] =
1 x
11
. . . x
1k
.
.
.
.
.
.
.
.
.
.
.
.
1 x
n1
. . . x
nk
.
Число строк n этой матрицы соответствует числу эксперимен-
тов, а число столбцов k + 1—числу факторов плюс первый столбец
из единиц, обеспечивающий оценку коэффициента β
0
. Методы ма-
тематической статистики, изложенные в предыдущих параграфах,
позволяют строить наилучшие оценки
ˆ
β
j
коэффициентов регрессии
β
j
зависимостей (20.1), (20.2) и исследовать их свойства.
Задачей математической теории планирования мн огоме рн ого экс-
перимента является изучение свойств этих оценок в зависимости от
выбора плана эксперимента, т.е. МПЭ, и построение оптимальных в
некотором смысле планов проведения экспериментов.
Замечание. В настоящем разделе курса речь идет лишь о матема-
тической теории планирования эксперимента, которая “работает”
лишь с формализованными моделями. Планирование эксперимента в
широком смысле слова включает в себя широкий комплекс вопросов,
в том числе вопросы выбора факторов, построения модели, органи-
зации, проведения эксперимента и др.
Глава 5 Планирование эксперимента 143
20.2 Цели планирования эксперимента и критерии оп-
тимизации
Напомним, что для модели (20.2), представленной здесь в мат-
ричной форме
Y = X
~
β + ~
ОНК коэффициентов регрессии
~
β имеют, согласно (19.5), вид
b =
ˆ
~
β = (X
0
X)
−1
X
0
y
где X—МПЭ, y—вектор наблюденных значений с.в. Y , причем
Mb = M
ˆ
~
β =
~
β (20.4)
C
b
= C
ˆ
~
β
= σ
2
(X
0
X)
−1
, (20.5)
так что ковариационная матрица оценок C
b
с точностью до посто-
янного множителя σ
2
совпадает с матрицей (X
0
X)
−1
, которую на-
зывают матрицей ошибок.
На последнем соотношении базируются как сама возможность
планирования эксперимента, так и цели и крите рии его качества.
Так как ковариационная матрица C
b
и матрица ошибок (X
0
X)
−1
не
зависят от вектора наблюдений y, то и свойства матрицы C
b
могут
быть исследованы до проведения эксперимента и независимо от него.
Боле того, так как C
b
= σ
2
(X
0
X)
−1
, то можно поставить задачу о
построении МПЭ таким образом, чтобы удовлетворить некоторым
требованиям, пред ъявляемым к матрице C
b
. Каковы могут быть эти
требования?
1) минимизация числа опытов при заданной точности;
2) простота вычислений;
3) композиционность плана — возможность использовать точки
проведения эксперимента для оценки параметров модели меньше-
го (например, 1-го) порядка для оценки параметров модели более
высокого (например, 2-го) порядка;
4) независимость оценок коэффициентов модели, т.е. требование,
чтобы ρ
b
i
,b
j
= 0, (такие планы называются ортогональными);

Глава 5 Планирование эксперимента 144
5) минимизация средней дисперсии оценок
¯
σ
2
(b) =
1
k
X
1≤i≤k
c
ii
=⇒ min;
6) минимизация максимальной дисперсии оценок
σ
2
max
(b) = max[c
ii
, i = 1, n] =⇒ min;
7) минимизация средней (максимальной) дисперсии выхода (G-
оптимальность);
¯
Dy =⇒ min, Dy[max y
j
; j =
¯
1, n] =⇒ min;
8) ротатабельность плана—независимость точности предсказания
от направления проведения эксперимента, а лишь от расстояния от
некоторой центральной точки и др.
20.3 Ортогональные планы
Ортогональные планы обладают многими хорошими из пере чис -
ленных выше свойств. Согласно определению для ортогонального
плана матрица C
b
= σ
2
(XX
0
)
−1
имеет диагональный вид. Стало
быть ди агональн а и матрица XX
0
,
XX
0
=
x
11
. . . x
n1
.
.
.
.
.
.
.
.
.
x
1k
. . . x
nk
×
x
11
. . . x
1k
.
.
.
.
.
.
.
.
.
x
n1
. . . x
nk
=
X
1≤k≤n
x
ik
x
kj
.
Отсюда, в частности, следует условие ортогональности плана
X
1≤l≤n
x
il
x
lj
= 0 при i 6= j, (i, j = 1, k). (20.6)
Таким образом, для модели (20.2) задача построения ортогональ-
ного плана сводится к выбору точек проведе ни я эксперимента таким
образом, чтобы удовлетворялось соотношение (20.6).
Глава 5 Планирование эксперимента 145
Для модели (20.1) эта задача сводится к выбору точек проведения
эксперимента так, чтобы
X
1≤l≤n
φ
i
(x
l1
, . . . , x
lk
)φ
j
(x
l1
, . . . , x
lk
) = 0 при i 6= j, (i, j = 1, r).
(20.7)
Это при водит к следующему понятию ортогональности системы
функций.
Определение 20.1. Система функций φ
i
(x) = φ
i
(x
1
, . . . x
k
) ( i =
1, r) называется ортогональной на множестве точек x
l
l = (1, n),
если выполнено соотношение (20.7).
Таким образом, при заданной системе функций φ
i
(x) = (i = 1, r)
эксперимент следует проводить в точках x
l
(l = 1, n), обеспечиваю-
щих ортогональность функций на ней. Возможен и другой подход:
если исследователь уже располагает экспериментами на множестве
точек x
l
(l = 1, n), то можно ставить задачу построения модели ви-
да (20.1) с ортогональной на заданном множестве системой функций
φ
i
(x) (i = 1, r).
20.4 Дополнения
Вопросы для контроля
1. Дайте опр еде лен ия:
а) линейной регрессионной модели,
б) матрицы плана эксперимента,
в) факторного п ростран ства,
г) функции и поверхности отклика,
д) ортогонального плана эксперимента.
2. В чем состоит задача математической теории планирования экс-
перимента?
3. Сформулируйте возможные цели планирования эксперимента.
4. Перечислите свойства ортогональных планов эксперимента.

Глава 5 Планирование эксперимента 146
§ 21 Полный и дробный факторные экспери-
менты
В настоящем разделе будут рассмотрены наиболее рас прос тра-
ненные ортогональные планы.
21.1 Полный факторный эксперимент типа 2
k
Одним из наиболее распространенных ортогональных планов яв-
ляется полный факторный эксперимент (ПФЭ) типа 2
k
и соответ-
ствующие ему д робные ре пли ки .
В общем случае полным факторным экспериментом следует на-
звать эксперимент, в котором реализуются все возможные сочетания
значений факторов.
Ясно, что для факторов, при ни мающих непрерывные значения,
ПФЭ невозможен. Поэтому для проведения этого эксперимента вы-
бирают определенные уровни варьирования факторов. Для оценки
функции отклика зависящей от k факторов, каждый из которых при-
нимает m значений, потребовалось бы m
k
опытов. Наиболее простым
ПФЭ является эксперимент типа 2
k
, состоящий в варьировании фак-
торов всего на двух уровнях. Этот вид эксперимента очень удобен
на н ачальной стадии проведения экспериментов.
Этапы проведения ПФЭ типа 2
k
состоят в следующем.
1. Выбирается экспериментальная область E факторного про-
странства X и по каждому фактору x
j
указывается нижний x
min,j
и верхний x
max,j
уровни варьирования, а также основной уровень
x
0,j
=
1
2
(x
min,j
+ x
max,j
) и полуинтервалы варьирования J
j
=
1
2
(x
max,j
− x
min,j
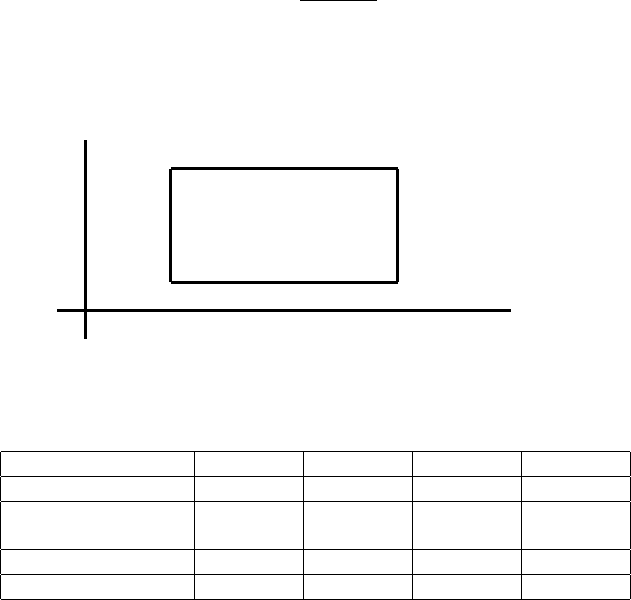
). Для случая двух факторов условия проведения
эксперимента представлены на рис.1. Условия проведения экспери-
мента полезно сохранить в виде таблицы 1.
2. Для унификации и облегчения расчетов факторы кодируются
путем изме нен ия масштабов по осям таким образом, чтобы значе-
ния всех факторов принимали соответственно значения ±1 и 0 для
верхнего, нижнего и основного уровней соответственно. Переход к
Глава 5 Планирование эксперимента 147
кодированным переменным осуществляется по формулам
X
ij
=
x
ij
− x
0j
J
j
,
где в отличие от натуральных перем енн ых x
ij
кодированные обозна-
чаются прописными буквами X
ij
- x
1
6
x
2
x
min,2
x
max,2
x
0,2
x
min,1
x
max,1
x
0,1
E
Рис. 1. План провед ени я двухфакторного эксперимента
Таблица 1.
Факторы x
1
x
2
x
3
x
4
Основной уровень x
0,1
x
0,2
x
0,3
x
0,4
Интервалы варьи-
рования
∆x
1
∆x
2
∆x
3
∆x
4
Верхний уровень x
max,1
x
max,2
x
max,3
x
max,4
Нижний уровень x
min,1
x
min,2
x
min,3
x
min,4
3. После кодирования значений факторов план проведения экспе-
римента представляется в виде таблицы. Для плана тип а 2
2
такая
таблица представлена ниже. При построении матриц планирования
эксперимента и соответствующих таблиц плана проведения экспери-
мента удобно пользоваться приемом чередования знаков, который
состоит в следующем: элементами нулевого столбц а (напомним, что
матрица плана эксперимента дополняется нулевым столбцом, обес-
печивающим оценку коэффициента β
0
) являются единицы, в первом

Глава 5 Планирование эксперимента 148
столбце знаки чередуются через 1, во втором — через 2 и т.д. Этот
прием, например, для ПФЭ типа 2
2
, содержащего n = 4 опыта, с
учетом нулевого столбца продемонстрирован в таблице 2.
Таблица 2.
№ опыта x
0
x
1
x
2
y
1 +1 -1 -1 y
1
2 +1 +1 -1 y
2
3 +1 -1 +1 y
3
4 +1 +1 +1 y
4
Матрица плана эксперимента в этом случае имеет вид
X =
1 −1 −1
1 +1 −1
1 −1 +1
1 +1 +1
.
21.2 Свойства полного факторного эксперимента
Являясь ортогональным планом ПФЭ обладает следующими
свойствами.
1. Симметричность относительно центра:
X
1≤i≤n
X
ij
= 0 (j = 1, k);
2. Ортогональность столбцов:
X
1≤i≤n
X
ij
X
ik
= 0 при j 6= k;
3. Нормировка:
X
1≤i≤n
X
2
ij
= n;

Глава 5 Планирование эксперимента 149
Из эти х основных свойств следует, что
X
0
X =
n 0 . . . 0
0 n . . . 0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 . . . n
(n+1)×(n+1)
и, с лед овательно,
(X
0
X)
−1
=
1
n
0 . . . 0
0
1
n
. . . 0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 . . .
1
n
(n+1)×(n+1)
.
Таким образом,
C
b
= σ
2
(X
0
X)
−1
=
σ
2
n
I
и, с лед овательно,
D(b
j
) =
σ
2
n
=
σ
2
(Y )
n
, cov(b
j
, b
k
) = 0.
Последнее свойство обеспечивает независимость оценок коэффици-
ентов линейной модели.
4. Независимость оценок коэффициентов линейной регрессии поз-
воляет строить для них доверительные интервалы и проверять их
значимость. Действительно,
b = (X
0
X)
−1
X
0
Y = (X
0
X)
−1
X
0
(X
~
β + ~) =
=
~
β + (X
0
X)
−1
X
0
~ ∈ N(
~
β, C
b
),
откуда b
j
∈ N(β
j
,
σ
2
n
), что дает возможность строить доверительные
интервалы для неизвестных коэффициентов регрессии. Если диспер-
сия ошибок наблюдения σ
2
известна, то доверительные интервалы
строятся на основе нормального распределения. Если же дисперсия
ошибок наблюдения не известна, то прибегают к статистике
t
m−1
=
b
j
− β
j
p
S
2
Y
√
m − 1
