Рыков В.В., Иткин В.Ю. Математическая статистика и планирование эксперимента

Подождите немного. Документ загружается.

Глава 4 Проверка статистических гипотез 100

и др. Р.А. Фишер предложил использовать последнее соотношение,

вычислил распределение соответствующей статистики и предложил

правило (критерий) проверки равенства дисперсий нормальных со-

вокупностей. Заметим, что величины nS

и mS

имеют χ

- и χ

распределения соответственно с n и m степенями свободы.

Для проверки гипотезы H

: σ

= σ

о равенстве дисперсий двух

выборок из нормальных совокупностей используется отношение

которое при выполнени и гипотезы H

: σ

= σ

имеет распределе-

ние отношения независимых нормированных своими м.о. с.в. имею-

щих χ

-распределения,

n−1,m−1

(n−1)σ

(m−1)σ

n−1

m−1

. (15.1)

Таким образом, для построения критерия и исследования его

свойств необходимо вычислить распределение статистики F

n,m

изучить его свойства. Это распределение впервые исследовал Р.А.

Фишер, поэтому оно называется распределением Фишера. Оно хо-

рошо изучено и табулировано. По названию распределения стати-

стики, основанный на ней критерий проверки равенства дисперсий

нормальных совокупностей также называется критерием Фишера.

15.3 F -распределение Фишера и его свойства

Определение 15.1. F

n,m

-распределением Фишера с n, m степеня-

ми свободы называется распределение с.в. F

n,m

, где χ

и χ

независимы и имеют χ

-распределения с n и m степенями свободы

соответственно (в обозначении распределения Фишера первым ука-

зывается число степеней свободы числителя n, вторым число степе-

ней свободы знаменателя m). С.в. F

n,m

принимает не отриц ательные

значения, ее распределение при n > 0, m > 0 имеет плотность

n,m







0, x < 0,

−1

(

)

(nx+m)

n+m

, x ≥ 0

(15.2)

Глава 4 Проверка статистических гипотез 101

вид которой для различных значений параме тров n > 0, m > 0

представлен на рис. ?. Здесь B(p, q) =

p−1

(1 − x)

q−1

dx — beta-

функция.

Моменты

Из формулы для п.р. распреде лен ия Фишера следует, что с.в.

n,m

имеет ограниченное число моментов. Действительно, для схо-

димости интеграла

p(x)dx

необходимо, чтобы

m+n

−

+ 1 − k > 1. Откуда m > 2k, так что

число моментов F

n,m

- распределения не больше, чем





. Непосред-

ственным вычислением можно убедиться, что м.о. и дисперсия F

n,m

распределения равны соответственно

µ = µ

m − 2

для m > 2, (15.3)

= µ

(0)

(n + m − 2)

n(m − 2)

(m − 4)

для m > 4. (15.4)

Связь между F

n,m

и F

m,n

, а также с B-распределением

Так как F

n,m

= F

−1

m,n

, то распределение и плотность с.в. F

m,n

можно получить исходя из распределения и плотности с.в. F

n,m

со-

ответственно.

m,n

(x) = P{F

m,n

≤ x} = P{F

−1

n,m

≤ x} =

= P



n,m

≥



= 1 − F

n,m





Для F

m,n

- распределения составлены подробные таблицы, а так-

же таблицы квантилей этого распределения. При использовании таб-

лиц удобно пользоваться последним свойством.

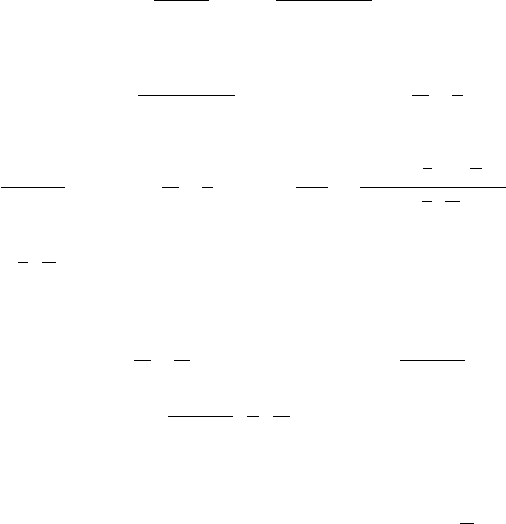
Глава 4 Проверка статистических гипотез 102

Отметим также связь F

m,n

-распределения с B-распределением.

Для этого заметим , что с.в.

B =



1 +

n,m



−1

m + nF

n,m

имеет распределение

(x) = P{B ≤ x} = P



m + nF

n,m

≤ x



= 1 −F

n,m



− 1



с плотностью

(x) =

(x)

= p

n,m



− 1



(1 − x)

−1

)

которая представляет собой частный случай B-распределения с па-

раметрами

. Таким обр азом, для вычис лен ия квантилей F -

распределения можно пользоваться также таблицами неполной β-

функции,

P{F

n,m

≤ x} = P





− 1



≤ x



= P



B ≥

m + nx



= 1 − B



m + nx

;



Асимптотика F

n,m

Так как с ростом m справедливо предельное соотношение

→

1 с вероятностью 1, то можно ожидать, что в этом случае nF

n,m

имеет приближенно χ

-распределение. Действительно, справедливо

утверждение.

Теорема 15.1. По вероятности и с вероятностью 1 имеет место

предельное соотношение

n,m

→ χ

Если число степеней свободы числителя и знаменателя независи-

мо друг от друга приближаются к бесконечности, F

m,n

- распределе-

ние приближается к нормальному, Точ нее сп равед лива

Глава 4 Проверка статистических гипотез 103

Теорема 15.2. По вероятности и с вероятностью 1 имеет место

предельное соотношение

n,m

− MF

n,m

→ N(0, 1).

Эти те орем ы докажите самостоятельно. См упражнение 3.

15.4 Свойства критерия Фишера

Для построения критерия (критической области) проверки ра-

венства дисперсий, основанного на статистике F

n,m

необходимо най-

ти по заданному размеру (уровню значимости) α 1 − α-квантиль

n,m

-распределения, т.е. точку c

такую, чтобы F

n,m

) = 1−α. То-

гда критическая область состоит из тех наблюдений x = (x

, . . . , x

y = (y

, . . . , y

), дл я которых

W =



x, y :

> c



Такая критическая область обеспечивает заданный размер крите-

рия. Рассмотрим ег о мощность. Пусть σ

6= σ

. Тогда отношение

n,m



/σ



по-прежнему имеет F

n,m

- распределение. Вычислим мощность кри-

терия

1 − β = P

(W ) = P



> c



= P



/σ



= 1 − F

n,m





Из последнего равенства видно, что мощность критерия убывает

с р остом отношения σ

/σ

и растет соответственно с ростом σ

/σ

Отсюда следует простое правило выбора для критерия одного из

двух возможных отношений F

n,m

= S

или F

m,n

= S

. Это

Глава 4 Проверка статистических гипотез 104

правило состоит в том, что из этих двух величин следует выбрать

ту, которая больше 1, т.е. в качестве числителя выбрать большую из

оценок. Это правило обеспечивает большую мощность критерия при

заданном его размере.

15.5 Применения критерия Фишера

Проверка однородности

Распространенным применением критерия Фишера является про-

верка однородности продукции, некоторых измерений и т.п.

Проверка адекватности регрессионной модели

На критер ии Фишера основывается также проверка адекватности

регрессионных м оделей. Уточним постановку задачи. Чтобы прове-

рить адекватность модели статистическими методами, надо сфор-

мулировать понятие адекватности в форме статистической модели.

Будем считать, что построенная регресс ионн ая модель адекватна на-

блюденным данным, если дисперсия отклонения наблюденных дан-

ных от предсказываемых моделью одинакова во всех точках фактор-

ного пространства. При этом гипотеза H

об адекватности модели

сводится к гипотезе о равенстве дисперсий.

15.6 Дополнения

Вопросы для контроля

1. Сформулируйте задачу о проверке равенства дисперсий.

2. Какие соотношения оценок дисперсий можно использовать в ка-

честве показателя их близости.

3. Сформулируйте задачу проверки адекватности регрессионных

моделей, основанную на критерии Фишера.

4. Сформулируйте и обоснуйте выбор критерия проверки о ра-

венстве дисперсий из двух возможных соотношений F

n,m

m,n

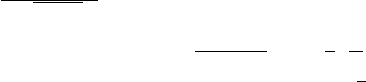
Глава 4 Проверка статистических гипотез 105

Упражнения

1. Вывести формулу (15.2) для п.р. F -распр еде лен ия отправляясь

от из вестной п.р. χ

-распределения.

2. Вычислить два момента F -распределения

3. Доказать:

а) F

n,m

→ χ

при m → ∞ по вероятности

б)

n,m

−EF

n,m

√

n,m

→ N(0, 1) при n, m → ∞ по вероятности

4. Доказать, что с.в. B =

m+nF

n,m

∈ B





5. Докажите, что F

m,n

(x) = 1 − F

n,m

(

). Какова связь F-

распределения с β-распределением?

Лабораторная работа

По заданным статистическим данным пользуясь средствами

Maple проверить гипотезы об их согласии заданным распределением

Глава 4 Проверка статистических гипотез 106

§ 16 Проверка сложных параметрических гипо-

тез при больших выборках

Рассмотренные в предыдущих разделах этой главы методы от-

носились в основном к проверке гипотез, связанных с нормальным

распределением. В настоящем параграфе будут рассмотрены некото-

рые вопросы проверки общих параметрических гипотез п ри больших

выборках.

16.1 Асимптотическое свойство отношения правдоподо-

бий.

Рассмотрим общий случай многомерного параметрического мно-

жества Θ размер ности r и пусть эксперимент состоит в простом слу-

чайном выборе, т.е. функция правдоподобия имеет вид

L(θ; x) = p(x

; θ) ···p(x

; θ).

Будем обозначать через θ

истинное значение параметра, а через U

некоторую его окрестность, и сделаем следующие предположения:

П.1. Для любых θ

, θ

∈ U

= θ

тогда и только тогда, когда

p(x; θ

) = p(x; θ

) поч ти всюду;

П.2. Функция φ(θ) = M

L(θ

;x)

L(θ;x)

непрерывна в точке θ

;

П.3. Функция L(θ; x) равномерно непрерывна в окрестности U

;

П.4. При любых n ≥ 1 и (x

, . . . , x

) ∈ χ

функция L(θ, x) имеет

единственный локальный максимум, и он достигается, т.е. оценка

максимального правдоподобия существует и совпадает с локальным

максимумом;

П.5. Функция L(θ; x) = p(x, θ) трижды дифференцируема по θ и все

ее частные производные ограничены.

Теорема 16.1. Если θ

— истинное значение параметра θ, и

λ(θ

, x) = λ

(x) =

(θ

, x)

sup

θ∈Θ

(θ, x)

(θ

, x)

(

θ, x)

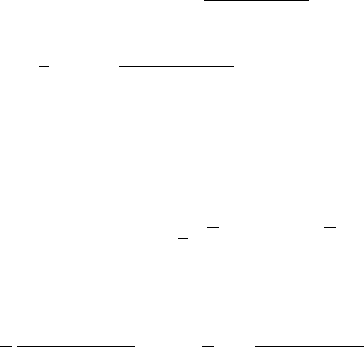
Глава 4 Проверка статистических гипотез 107

Тогда при выполнении условий П.1–П.5 имеет место предельное со-

отношение

−2 ln λ

(θ

; x) = 2 ln L

(

θ; x) − 2 ln L

(θ

; x) → χ

где r - размерность параметрического множества Θ.

Доказательство. 1) Разложим функцию

ln L

(θ; x) =

k=1

ln p(x

; θ)

в ряд Тейлора в окрестности случайной точки

θ. Имеем:

ln L

(θ, x) = ln L

(

θ, x) +

1≤i≤r

∂ ln L

(θ, x)

∂θ



θ=

(θ

−

) +

1≤i,j≤r

∂

ln L

(θ, x)

∂θ



θ=

(θ

−

)(θ

−

) + R,

или полагая θ = θ

и записывая это соотношение в векторной форме,

получим

ln L

(θ

, x) − ln L

(

θ, x) = (grad ln L

(

θ, x), (θ

−

θ)) +

√

n(θ

−

θ)

√

n(θ

−

θ) + R,

где A – случайная матрица с элементами

∂

ln L

(θ, x)

∂θ



θ=

k=1

∂

ln p(x

, θ)

∂θ



θ=

2) Так как элементы матрицы A есть средние арифметические

с.в., то при n → ∞ по ЗБЧ пр и гипотезе H

имеет место сходимость

Глава 4 Проверка статистических гипотез 108

по ве роятности

→ M

∂

ln p(x, θ)

∂θ

∂

ln p(x, θ)

∂θ

p(x, θ)dx =

∂

∂θ



∂p

∂θ



p(x, θ)dx = −

∂p

∂θ

∂p

∂θ

p(x, θ) dx +

∂

p(x, θ)

∂θ

= −



∂p

∂θ



∂p

∂θ



p(x, θ)dx +

∂

∂θ

p(x, θ)dx =

= −M



∂ ln p(x, θ)

∂θ

∂ ln p(x, θ)

∂θ



т.е. A → B

= −M

∂ ln p(x, θ)

∂θ

∂ ln p(x, θ)

∂θ

3) Из метода максимального правдоподобия следует, что

, как

оценка максимального правдоподобия асимптотически норм альна с

= θ

и D

= M

(

− θ

)

= B

, т.е.

√

− θ

) → N(0, B

−1

4) Таким образом,

2 ln L

(

, x) − 2 ln L

(θ

, x) →

ξ по вероятности,

где

ξ ∈ N(0, B

−1

). Далее, так как B

–положительно определенная

матрица, то существует B такая, что B

= B, и B

= B

B = B

. Обо-

значим ~η = B

ξ, тогда ~η ∈ N(0, I) и

ξ =

ξ = ~η

~η. Другими

словами,

−2 ln λ

= 2 ln L

(

θ, x) − 2 ln L

(θ

, x) → ~η

~η =

i=1

где r – размерность параметрического пространства.

Таким образом, доказанная теорема поз воляет предложить метод

проверки параметрических гипотез при больших выборках, а имен-

но: если n велико, то выбирая в качестве статистики критерия функ-

цию отношения правдоподобий λ

построим критическую область в

виде

W = {x : −2 ln λ

> c

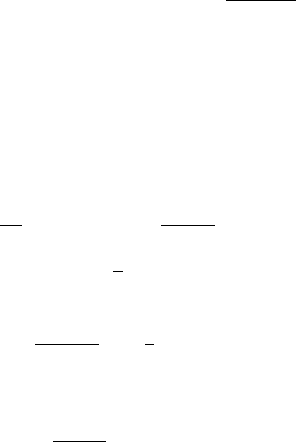
Глава 4 Проверка статистических гипотез 109

где постоянная c

легко вычисляется по заданному размеру крите-

рия из с оотношен ия

(W ) = P

{−2 ln λ

> c

} = P{χ

> c

так как при выполнении гипотезы H

статистика −2 ln λ

асимпто-

тически имеет χ

-распределение с r степенями свободы.

16.2 Пример

Рассмотрим применение предл оженного метода для проверки ги-

потезы о параметре распределения Пуассона. Пусть θ-истинное зна-

чение параметра распределения Пуассона. Функция правдоподобия

в этом сл учае имее т вид

(θ; x) = p(x, θ) =

k=1

p(x

; θ) =

k=1

!...x

−nθ

так что

l(θ, x)) = ln L

(θ, x) = −nθ +

k=1

ln θ − ln(x

!...x

!),

∂

∂θ

l(θ, x) = −n +

k=1

= 0.

Откуда легко найдем ОМП

θ =

k=1

. Таким образом,

λ(θ, x) =

L(θ, x)

θ, x)





k=1

θ−θ)







nθ

k=1







k=1

exp

k=1

− nθ