Рубин А.Б., Пытьева Н.Ф., Ризниченко Г.Ю. Кинетика биологических процессов

Подождите немного. Документ загружается.

мальной химической кинетики является следствием следующих

предположений.

1. О независимости состояний взаимодействующих компонентов

цепи

переноса электронов.

2. О существовании «перекрестных» взаимодействий

между

со-

седними переносчиками элементарных цепочек ансамбля.

Обсудим условия, при которых названные предположения, а

следовательно, и бимолекулярное описание справедливы. Так, пер-

вое предположение может выполняться в «открытой» электрон-

транспортной цепи, осуществляющей обмен электронами с окру-

жающей средой, и заведомо не выполняется в том случае, если

система переноса является «замкнутой» (т. е. электроны не

поки-

дают

эту систему и не поступают в нее извне), и притом в каждой

элементарной

цепи имеется («циркулирует») лишь один «подвиж-

ный» электрон. Последнее условие реализуется в случае, когда все

переносчики

цепи, кроме одного, исходно находятся в окисленном

состоянии.

События D~ и Л

нельзя считать независимыми, и сле-

дует

рассматривать условную вероятность p(A

/D~). Пусть, на-

пример,

в данный момент времени молекула D находится в вос-

становленном состоянии,

тогда

событие А

достоверно, т. е. услов-

ная

вероятность

p(A

/D~)

= l. Выполнив с

учетом

этого равенства

описанную выше процедуру суммирования и усреднения по ансам-

блю элементарных цепочек, получим для макроскопических нере-

менных систему линейных дифференциальных уравнений, т. е. так

называемое псевдомономолекулярное описание электрон-транс-

портных процессов.

Второе предположение о существовании «перекрестных» взаи-

модействий элементарных электрон-транспортных цепочек, по-ви-

димому, также не всегда справедливо. Оно может реализоваться

на

участках цепи, включающих пуловые компоненты, и не выпол-

няется

для компонентов, входящих в состав реакционных центров.

Так,

например, имеются данные о том, что каждая возбужден-

ная

молекула фотоактивного пигмента передает электрон лишь

одной,

«своей»

молекуле первичного акцептора. Вместе с тем на

уровне вторичных акцепторов и цитохромов (первичных доноров),

по-видимому, имеет место перекрестный обмен электронами.

В пользу существования на указанных участках цепи таких пере-

крестных взаимодействий свидетельствуют и результаты математи-

ческого моделирования. Так, лишь в рамках бимолекулярного опи-

сания

удается объяснить наблюдаемые в опытах закономерности

редокс-превращений цитохромов.

В случае, если ансамбль состоит из невзаимодействующих,

«изолированных»

друг

от

друга

элементарных цепочек, удобнее

использовать иной подход, в котором в отличие от прежнего в

качестве динамических переменных рассматриваются вероятности

различных состояний всей цепи в целом.

Как

и прежде,

будем

считать, что каждый переносчик может

находиться только в

двух

состояниях: однократно окисленном или

271

однократно восстановленном. Тогда цепь, включающая

перенос-

чиков,

будет

характеризоваться «произведением»

2-2- ... -2, т. е.

различными состояниями,

между

некоторыми из которых воз-

можны переходы. Поясним сказанное на примере элементарной

электрон-транспортной цепи, состоящей из

двух

переносчиков:

ft,

к,

-+D-+A-+-. (IV Л —14)

Все возможные состояния цепи таковы:

D+A+;

= D~A+; E

D+A—,

= D~A~.

Введем важное для дальнейшего понятие р(Е

{

, t) = pi— вероят-

ность того, что в момент времени t рассматриваемая система на-

ходится в состоянии Е

{

. Задача кинетического описания системы

заключается в выяснении временного поведения этих вероятностей.

Определив вероятность каждого состояния системы в целом, мы

получаем полную информацию о состоянии любого переносчика,

просуммировав вероятности

всех

тех состояний комплекса, в кото-

рых данный переносчик находится в интересующей нас форме

(окисленной

или восстановленной). Так, сумма pi + рг

дает

ве-

роятность пребывания переносчика А в данный момент времени в

окисленной

форме.

Переходы

между

состояниями системы, обусловленные элек-

трон-транспортным процессом,

будем

рассматривать как однород-

ный

марковский процесс с конечным числом состояний и непре-

рывным временем. Предположим для простоты, что из состояния

Ei система может перейти в состояние Е

и только в Е

и что

переходы типа

-^-ЕХ

«запрещены». Предположим также, что ве-

роятность такого перехода за время dt равна

= k

dt. (IV. 1-15)

Тогда вероятность того, что в момент времени t + dt система

будет

находиться в исходном состоянии Ei, равна

(t + dt)

=••

(0(1- a

(IV. 1-16)

Из

уравнения (IV.1 —16) нетрудно получить выражение для ско-

рости изменения во времени вероятности застать систему в дан-

ном

состоянии

J2L = -k

lmPl

{t). (IV. 1-17)

В общем

случае

изменение состояния системы может происхо-

дить за счет нескольких «разрешенных» переходов.

Диаграмма всевозможных переходов в системе (IV.1 —14) из

двух

переносчиков показана на рис. IV.3. Направление переходов

изображено стрелками. На основе такой диаграммы легко соста-

272

вить кинетические уравнения для вероятностей состояний рассмат-

риваемой системы. Скорость изменения данного состояния опре-

деляется суммой

«входящих

потоков», за вычетом «потоков», вы-

водящих систему из данного состояния (выходящие стрелки).

Таким образом, вектор-функция p(t) = [pi(t), ..., p

(t)]

удовлет-

воряет следующей системе линейных дифференциальных уравне-

ний:

(t)

(IV.1 — 18)

где элементами матрицы коэффициентов К являются константы

переходов

между

состояниями системы k

, а диагональные элемен-

ты равны k

= —S\k

. Поскольку переходы

между

состояниями

комплекса обусловлены переносом электронов от одного перенос-

чика к

другому

или обменом электронами

между

переносчиками

средой, каждой константе перехода

между

состояниями k

от-

вечает одна из обычных констант ско-

ростей транспорта электронов k

{

. При

этом разным константам переходов

kim

могут

соответствовать, вообще го-

воря,

одни и те же константы перено-

са ki. Так, показанные на диаграмме

(IV. 1—3) переходы из состояний

Ei(D+A+), E

(D+A-) в состояния

(D~A

), Ei(D-, Л~) происходят за

счет притока электронов в цепь извне

и,

следовательно, характеризуются од-

ной

и той же константой k\. Переход

(О~А

)—*Ez{D

A~)

означает пере-

нос

электрона внутри системы от мо-

лекулы D на молекулу А с константой

скорости k

. Переходы

—*Е

—>-Е\

обусловлены оттоком

электронов из системы и характеризуются константой скоро-

сти k

Таким образом, кинетические уравнения — обычные уравнения

баланса для состояний рассматриваемой системы — имеют вид

Ко

Рис.

IV.3. Диаграмма состояний

модельной системы (IV.

—13)

dpi

(IV.1—19)

КРъ — (&i + h)

273

где ki — соответствующие константы скоростей. Порядок системы

(IV.1 —19) можно понизить, использовав условие нормировки:

Pi-r-ft-Ps-f-/>4=l. (IV. 1-20)

которое легко получить, сложив исходные уравнения. Смысл со-

отношения

(IV.1 —15) ясен: в каждый момент времени система

должна находиться в одном из четырех возможных состояний, так

что сумма рассматриваемых событий является достоверным собы-

тием.

Существенным преимуществом сформулированного описания

электрон-транспортных процессов является линейный характер ки-

нетических уравнений и, следовательно, возможность их аналити-

ческого исследования. Для упрощения обычной процедуры реше-

ния

этих уравнений удобно использовать диаграммные (графиче-

ские)

методы, разработанные, например, для описания процессов

мембранного транспорта (Hill, 1971, 1972; Маркин, Чизмаджев,

1974). Изложение диаграммной техники и вопросов обоснования

этого метода выходит за рамки нашей книги. Отметим лишь, что

для метода существенно, чтобы объект исследования можно было

описывать в терминах дискретных состояний,

между

которыми

происходят переходы. Каждое состояние обозначается точкой на

плоскости;

переходы обозначаются линиями, соединяющими соот-

ветствующие точки.

помощью метода диаграмм (графов) особенно удобно иссле-

довать стационарные процессы. Этот метод очень широко исполь-

зуется для анализа стационарной кинетики ферментативного ка-

тализа (Волькенштейн, 1966, 1975), стационарного мембранного

транспорта. Не останавливаясь подробно на отдельных этапах

графического решения задачи, описание которых читатель может

найти

в рекомендуемой литературе, отметим, что диаграммный

метод позволяет так формализовать процесс отыскания стационар-

ных состояний системы, что не требуется

даже

«выписывание» ис-

ходных дифференциальных уравнений.

В заключение

следует

отметить, однако, что изложенный спо-

соб описания электрон-транспортных процессов наряду с опреде-

ленными

достоинствами обладает и недостатками. Дело в том, что

число состояний электрон-транспортной цепи, а следовательно, и

число кинетических уравнений для вероятностей этих состояний

катастрофически растет с увеличением числа переносчиков — как

. Если при этом попытаться

учесть

перекрестные взаимодействия

элементарных цепочек в ансамбле, количество уравнений становит-

ся

труднообозримым и может оказаться затруднительным

даже

составление диаграммы переходов

между

возможными состояния-

ми

системы. В этом

случае

удобнее использовать традиционный

подход

и записывать дифференциальные уравнения для состоя-

ний

отдельных переносчиков, как это было продемонстрировано

выше.

274

При

построении математических моделей электрон-транспорт-

ных процессов, как правило, исходят из предположения о постоян-

стве констант скоростей реакций во времени и их независимости

от состояния переносчиков. При этом численные значения кон-

стант задают в соответствии с экспериментально полученными

оценками,

которые, однако, имеются отнюдь не для

всех

стадий

рассматриваемого процесса. Таким образом, задача математиче-

ского моделирования включает в качестве необходимого этапа

оценку

тех параметров рассматриваемой цепи, которые не подда-

ются прямому экспериментальному определению.

Первичным

процессам фотосинтеза свойственна ярко выражен-

ная

временная иерархия: отдельные реакции переноса электронов

протекают в исключительно широком диапазоне скоростей с харак-

терными временами (ti ) от

10~

-т-10~

секунд до нескольких ми-

нут. Казалось бы, столь существенное различие характерных вре-

мен

отдельных стадий процесса может служить основой примене-

ния

метода квазистационарных концентраций и упрощения соот-

ветствующей математической модели. Тем не менее прямое при-

менение

теоремы Тихонова к системам кинетических уравнений

электронного

транспорта в большинстве случаев оказывается за-

труднительным. Рассмотрим подробнее причины затруднений, воз-

никающих при попытках упрощения моделей электрон-транспорт-

ных процессов.

Как

было показано в гл. 8 первой части книги, теорема Тихо-

нова

отражает объективное расслоение динамических переменных

системы на быстрые и медленные, о чем свидетельствует наличие

малого параметра перед соответствующими производными. След-

ствием такого расслоения системы является квазистационарное те-

чение моделируемого процесса, т. е. возможность замены быстрых

переменных их стационарными значениями. В

случае

электрон-

транспортных процессов свойственная отдельным стадиям времен-

ная

иерархия не всегда обеспечивает необходимое для применения

теоремы Тихонова разделение переменных на быстрые и значи-

тельно более медленные. Дело в том, что приведенные выше оцен-

ки

характерных времен или констант скоростей отдельных стадий

определяют скорость транспорта электронов лишь при наиболее

благоприятных условиях, т. е. в случае, когда процесс не лими-

тирован состоянием переносчиков (способностью их отдать или

принять

электрон). В общем

случае

«быстрота»

изменения макро-

скопических переменных модели определяется не только констан-

тами скоростей соответствующих реакций (значения которых мо-

гут варьировать в весьма широких пределах), но и величинами

входящих в уравнения концентраций реагентов. Эти концентрации,

свою очередь,

могут

быть таковы, что, несмотря на весьма высо-

кие

значения констант, величины соответствующих электронных

потоков

(скоростей реакций) отнюдь не велики. При этом резуль-

тирующие скорости окислительно-восстановительных превращений

275

отдельных компонентов системы сравнимы по величине, так что

выделение малого параметра и расслоение переменных на быстрые

медленные оказывается невозможным.

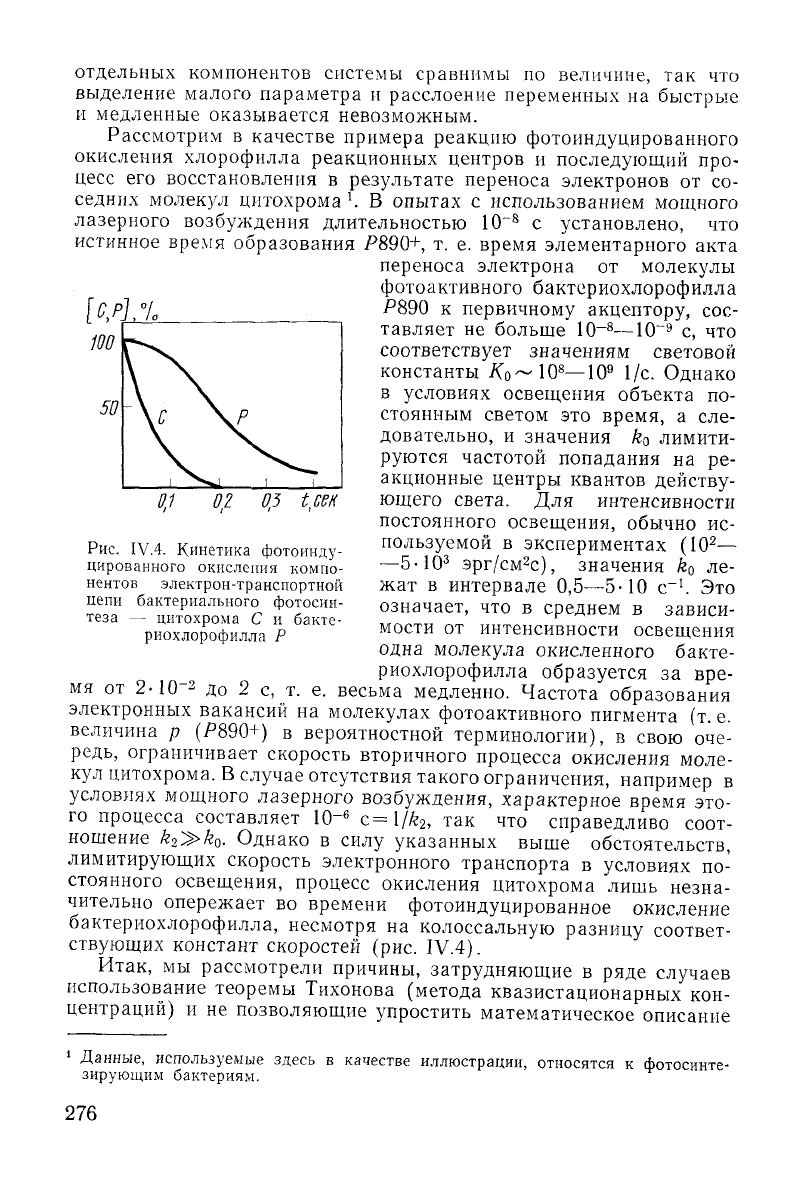
Рассмотрим в качестве примера реакцию фотоиндуцированного

окисления

хлорофилла реакционных центров и последующий про-

цесс его восстановления в

результате

переноса электронов от со-

седних молекул цитохрома

. В опытах с использованием мощного

лазерного возбуждения длительностью 10~

с установлено, что

истинное

время образования Р890+, т. е. время элементарного акта

переноса электрона от молекулы

фотоактивного бактериохлорофилла

Р890

к первичному акцептору, сос-

тавляет не больше

10~

—10~

с, что

соответствует

значениям световой

константы

/Со

—

—10

1/с. Однако

условиях освещения объекта по-

стоянным

светом это время, а сле-

довательно, и значения k

лимити-

руются

частотой попадания на ре-

акционные

центры квантов

действу-

ющего света. Для интенсивности

постоянного

освещения, обычно ис-

пользуемой в экспериментах (10

—

—5-Ю

эрг/см

с), значения k

ле-

жат в интервале

0,5—5-10

с"

. Это

означает, что в среднем в зависи-

мости от интенсивности освещения

одна молекула окисленного бакте-

риохлорофилла образуется за вре-

мя

от 2-10

до 2 с, т. е. весьма медленно. Частота образования

электронных вакансий на

молекулах

фотоактивного пигмента (т. е.

величина р

(Р890+)

в вероятностной терминологии), в свою оче-

редь, ограничивает скорость вторичного процесса окисления моле-

кул цитохрома. В

случае

отсутствия такого ограничения, например в

условиях мощного лазерного возбуждения, характерное время это-

го процесса составляет 10"

с=1/&

, так что справедливо соот-

ношение

'>k

Однако в силу указанных выше обстоятельств,

лимитирующих скорость электронного транспорта в условиях по-

стоянного

освещения, процесс окисления цитохрома лишь незна-

чительно опережает во времени фотоиндуцированное окисление

бактериохлорофилла, несмотря на колоссальную разницу соответ-

ствующих

констант скоростей (рис.

IV.4).

Итак,

мы рассмотрели причины, затрудняющие в ряде

случаев

использование теоремы Тихонова (метода квазистационарных кон-

центраций)

и не позволяющие упростить математическое описание

Данные, используемые здесь в качестве иллюстрации, относятся к фотосинте-

зирующим бактериям.

0.1 02 05

tceH

Рис.

IV.4. Кинетика фотоинду-

цированного окисления компо-

нентов электрон-транспортной

цепи

бактериального фотосин-

теза

— цитохрома С и бакте-

риохлорофилла Р

276

реакций

переноса электронов. Существуют, однако, и

другие

об-

стоятельства, обусловленные конкретными целями моделирования

электрон-транспортных процессов, в силу которых соответствую-

щие

математические модели содержат больше

двух

уравнений и,

следовательно, трудно поддаются простому качественному иссле-

дованию. Казалось бы, такие модели противоречат принципу про-

стоты, сформулированному в работе Романовского и

других

(1975),

который

гласит: модель биологического процесса должна содер-

жать минимальное число уравнений, необходимое для описания

основных функций объекта моделирования. Однако, как

будет

по-

казано

ниже, в большинстве математических моделей биологиче-

ских процессов электронного транспорта решение поставленной

задачи, в том числе описание основных функций объекта и выяс-

нение

механизмов регуляций, достигается лишь путем детального

сравнения

теоретических и экспериментальных характеристик ки-

нетики

рассматриваемых процессов. Мы уже говорили, что экспе-

риментальные характеристики объекта относятся к отдельным,

спектрально идентифицированным компонентам, которые непосред-

ственно взаимодействуют

друг

другом

в электрон-транспортной

цепи.

Следовательно, с этой точки зрения, модель должна содер-

жать уравнения, описывающие кинетику окислительно-восстанови-

тельных превращений реальных компонентов независимо от

«быст-

роты»

этих превращений. Чем больше компонентов цепи поддается

прямому экспериментальному измерению, тем больше возможно-

стей для проверки правильности модели, но вместе с тем и больше

число независимых уравнений.

Одной из задач математического моделирования может являть-

ся

и выяснение вопроса о

«полноте»

наших знаний относительно

организации

цепи переноса электрона и о возможности существо-

вания

дополнительных, спектрально неидентифицированных ком-

понентов.

Очевидно, в этом

случае

полная модель должна содер-

жать уравнения, описывающие кинетику изменения во времени

дополнительных гипотетических компонентов и учитывающие воз-

можные способы взаимодействия этих компонентов с известными

переносчиками.

В главе 8 первой части книги отмечалось, что в большинстве

случаев упрощенные модели биологических объектов оказываются

«лучше»

сложных, так как допускают качественное исследование

поведения модельной системы в достаточно широкой области из-

менения

параметров и тем самым

дают

более полные представле-

ния

об объекте. Напротив, в сложной системе варьирование боль-

шого числа независимых параметров в широких пределах оказы-

вается весьма трудоемким, поэтому зачастую поведение таких

систем удается исследовать лишь в отдельных частных

случаях,

при

определенных комбинациях коэффициентов. Как же преодо-

леть эту трудность при теоретическом исследовании биологических

277

электрон-транспортных процессов, если в соответствии с задачами

такого исследования математическая модель оказывается сложной,

содержащей большое число независимых переменных и парамет-

ров? Дело в том, что в данном

случае

нет нужды исследовать по-

ведение модели в широком диапазоне значений констант, так как

многие из этих констант весьма точно измерены экспериментально,

а относительно

других

известны предварительные оценки. Таким

образом, остается сравнительно небольшое число неизвестных па-

раметров, значения которых необходимо определить на основе

исследования модели. Отметим, что благодаря широким возмож-

ностям

экспериментальной проверки модели — по многим незави-

симым характеристикам,—в отдельных случаях возможно доста-

точно точное определение неизвестных ранее значений параметров

цепи.

В силу перечисленных обстоятельств, обусловленных особен-

ностями

объекта и задач математического моделирования, лишь

самые начальные этапы теоретического исследования электрон-

транспортных процессов (нахождение особых точек соответствую-

щих систем дифференциальных уравнений, анализ их типа и устой-

чивости) проводятся качественными методами, изложенным!! в

первой части книги. Основная же доля работы с моделью выпол-

няется

с помощью вычислительных устройств (аналоговых или

цифровых) — путем численного интегрирования соответствующих

уравнений.

Ниже

мы остановимся кратко на отдельных примерах матема-

тических моделей, разработанных для описания электрон-транс-

портных процессов, а затем перейдем к более детальному изложе-

нию

результатов выполненного авторами теоретического исследо-

вания

процессов переноса электронов при фотосинтезе.

Глава

ПРИМЕРЫ

МАТЕМАТИЧЕСКИХ

МОДЕЛЕЙ

БИОЛОГИЧЕСКИХ

ПРОЦЕССОВ

ЭЛЕКТРОННОГО

ТРАНСПОРТА

В последние годы число работ, посвященных математическому

моделированию биологического транспорта электронов, быстро

растет.

Авторы

не ставили своей целью дать исчерпывающий об-

зор таких работ, поскольку он был бы интересен только узкому

кругу

специалистов. Ограничимся рассмотрением лишь отдельных

примеров,

из которых был бы ясен круг задач, стоящих перед ма-

тематикой в данной области биологин, и характер полученных

результатов.

278

Начало исследований в области математического моделирова-

ния

электрон-транспортных процессов фотосинтеза и дыхания бы-

ло положено Б. Чансом с сотрудниками

(1940,

1963). Объектом

моделирования в первых работах этих авторов явилась последо-

вательность реакций дыхания митохондрий, которую можно изо-

бразить в виде следующей упрощенной схемы:

Здесь с, а, а

— компоненты цитохромной цепи, &; — константы

скоростей рассматриваемых реакций.

Процесс переноса электронов, например, для пары железо-

протеинов а, а

можно представить следующей последовательно-

стью химических реакций:

+ 4

-Д

al+

+ 0.

-I ар' 07.

Соответствующие дифференциальные уравнения, выведенные на

основе закона действующих масс, имеют вид

-|- [а*+] = К №+] [а

+] - К [а*+]

[аР-],

J N

4+] - К

[О,]

[al

(IV.2-2)

Аналогичные уравнения

могут

быть записаны для каждого из ком-

понентов рассматриваемой цепи. Вследствие нелинейного харак-

тера этих уравнений их исследование было выполнено с помощью

аналогового вычислительного устройства. Результаты проведен-

ного исследования модели позволили авторам сформулировать так

называемую теорему пересечения —

«cross-link»,

на основании ко-

торой были разработаны экспериментальные тесты для идентифи-

кации

звеньев электрон-транспортной цепи, сопряженных с

энер-

гетическими процессами.

В основе теоремы пересечения лежит хорошо известный эффект

замедления скорости переноса электронов при удалении из систе-

мы субстратов фосфорилирования АДФ и фосфата Ф. При этом

некоторые переносчики цепи переходят в более восстановленную

форму, а

другие-—в

более окисленную. Теорема может быть ис-

пользована не только для идентификации участков электрон-транс-

портной цепи, сопряженных с фосфорилированием, но в равной

степени применима к поиску повреждений в линейной электриче-

ской

цепи сопротивлений.

Опыт авторов (Чане, 1963) показал, что использование метода

математического моделирования способствует более глубокому

изучению экспериментальной системы. Так, например, названный

метод позволил рассчитать количественные соотношения перенос-

279

чиков

дыхательной цепи. В частности, было показано, что концен-

трации

всех

цитохромов и флавопротеидов равны и примерно в

10 раз превышают концентрацию пиридиннуклеотидов. Таким об-

разом,

первые попытки математического моделирования электрон-

транспортных процессов оказались весьма плодотворными.

Впоследствии эти же авторы использовали

метод

математиче-

ского моделирования для анализа более сложных процессов взаи-

модействия системы переноса электронов с метаболической актив-

ностью клетки. Были исследованы механизмы регулирования

обмена в раковых клетках. Соответствующая модель включала

двадцать кинетических уравнений: пять уравнений, связанных с

функцией

фосфорилирования глюкозы, семь — с гликолитическим

фосфорилированием

АДФ, пять — с окислительным фосфорилиро-

ванием

АДФ и три — с утилизацией и переносом АТФ. Названные

уравнения содержали три типа членов: диффузионные (скорость

реакции

пропорциональна концентрации только одного вещества);

билинейные

(скорость реакции пропорциональна произведению

двух

веществ) и члены, описывающие реакции, скорость которых

пропорциональна

произведению

трех

реагентов. Уравнения решали

при

помощи обычных цифровых интегрирующих устройств. В рас-

четах

были использованы экспериментально определенные вели-

чины

некоторых констант скоростей. На модели был получен ряд

экспериментально

наблюдаемых эффектов, в частности эффект

Кребтри — торможения утилизации кислорода при добавлении в

систему глюкозы, а также явление реактивирования обмена

опухо-

левой клетки под действием агентов, разобщающих электронный

транспорт с фосфорилированием.

Вместе

с тем

результаты

цитируемой работы показывают, что

анализ

столь сложной модели является исключительно трудоемкой

задачей в силу практически неограниченного произвола в выборе

численных значений параметров (констант скоростей и начальных

условий). По этой причине вопрос о степени адекватности сформу-

лированной

модели реальному

объекту

остался невыясненным. Ав-

торы признают, что перспективы моделирования такой многоком-

понентной

системы и пределы применимости

метода

в столь слож-

ных ситуациях отнюдь не очевидны. По-видимому, увеличение

числа независимых динамических переменных модели разумно

лишь

в определенных

пределах.

В области фотосинтеза одной из первых попыток моделирова-

ния

электрон-транспортных процессов явилась работа Френча и

Форка,

основанная на гипотезе об участии в фотосинтезе водорос-

лей

двух

фотосистем и построенная с

учетом

кислородного обмена

(French,

Fork,

1961).

На рис. IV.5 показана упрощенная

схема

реакций,

использованная авторами названной работы в качестве

объекта моделирования. Схема включает две фотореакции: длин-

новолновой

пигментной системы

А-1х

280