Рубан А.И. Методы анализа данных. Практикум
Подождите немного. Документ загружается.

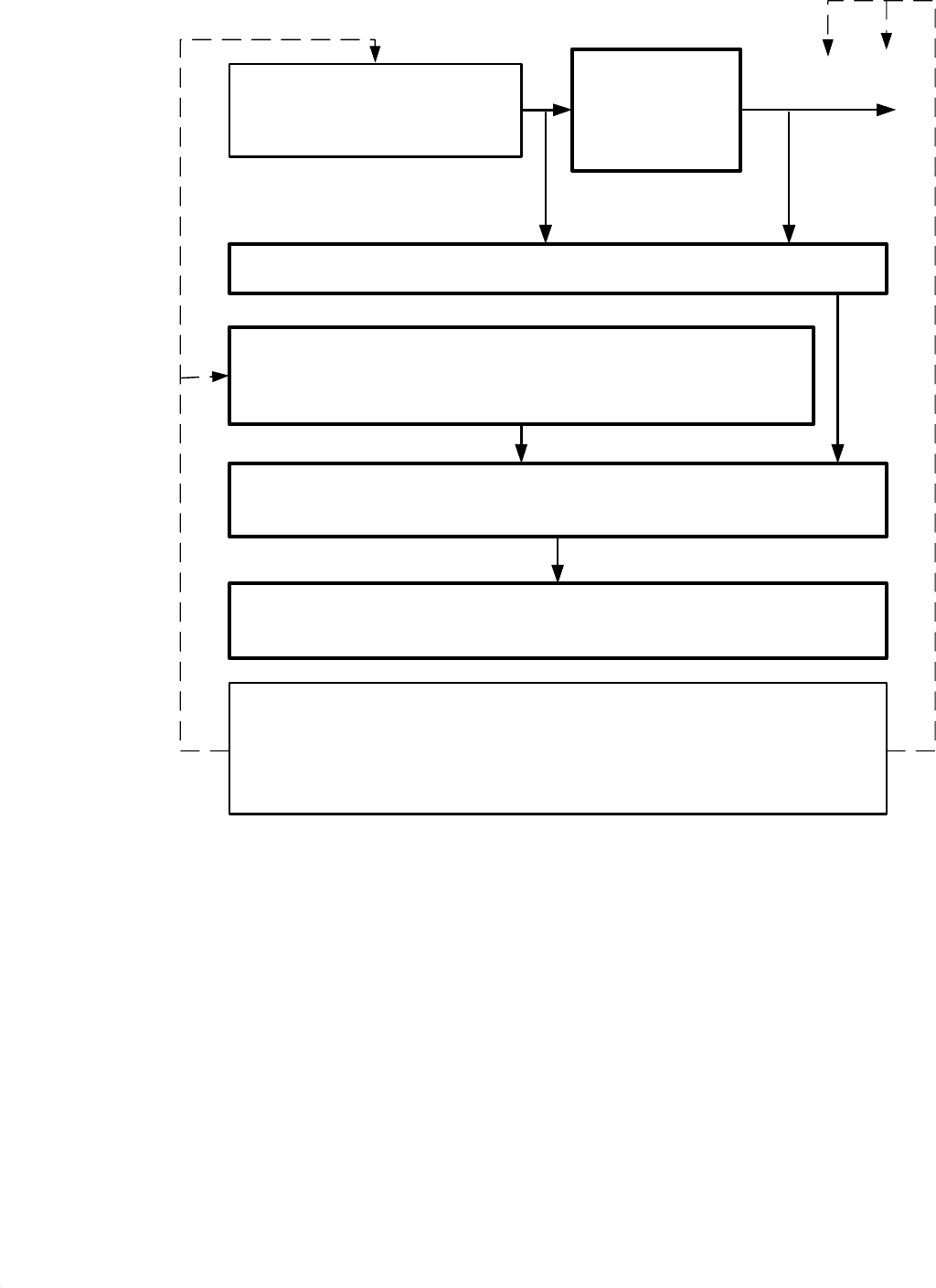
41
Объект
Расчёт показателя близости непараметрической оценки
регрессии и сигнальной части выхода объекта
h
x
y
+
ϕ
=
)
(
Генерирование
значений входного
воздействия
База экспериментальных данных входов и выходов
объекта
Исследователь может менять вид входного
воздействия, виды ядер, критерии оптимальности и
алгоритмы оптимизации
при подстроке коэффициента размытости, а также
сигнальную часть и помеху (при имитации объекта)
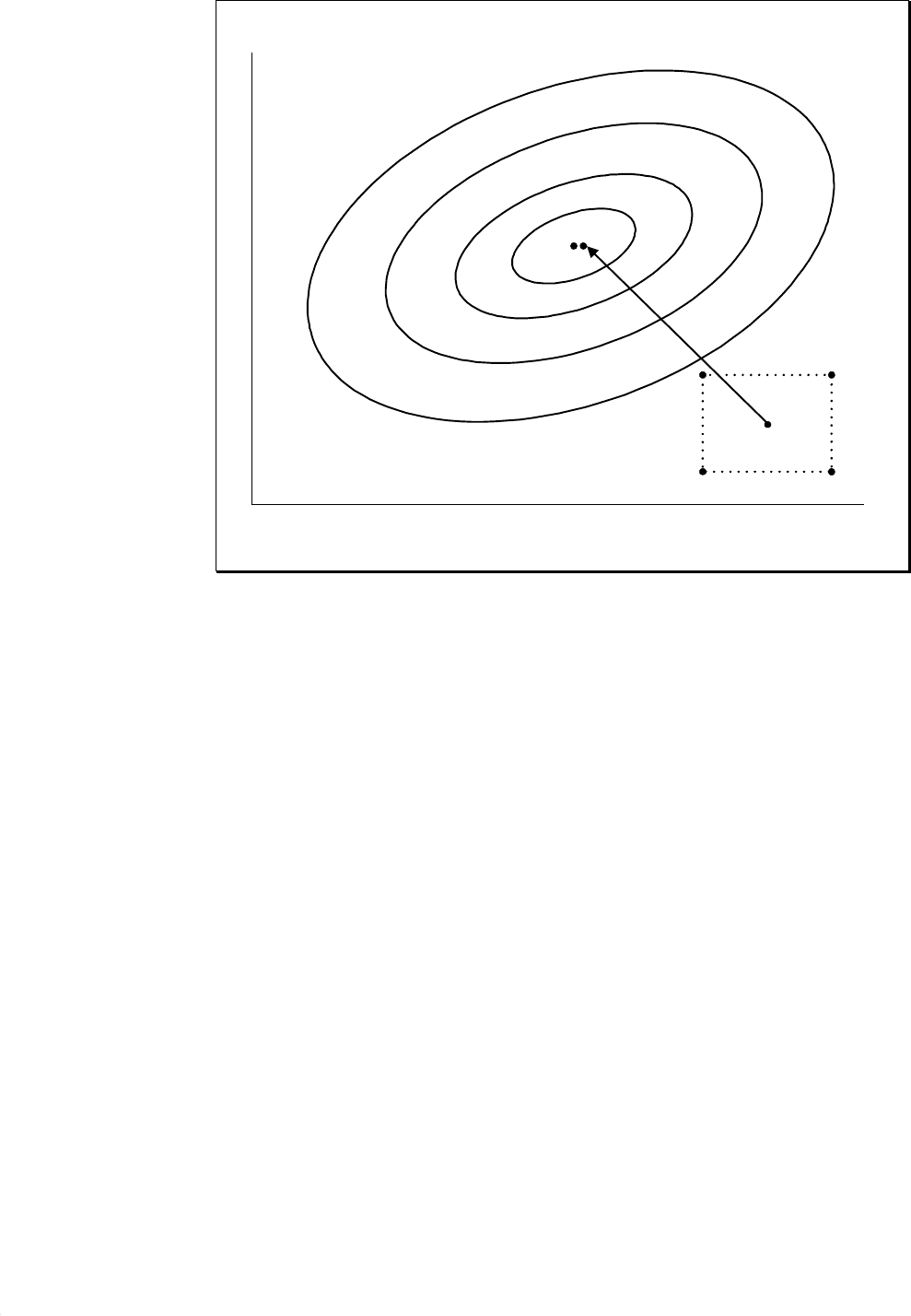
Рисунок 6.2. Блок-схема последовательности выполнения
операций
при построении и исследовании непараметрической оценки
Задание вида ядра непараметрической оценки
регрессии, критерия оптимальности и алгоритма
оптимизации
Расчёт коэффициента размытости ядра
непараметрической оценки регрессии
6.3 Исследование непараметрической оценки инверсной регрессии
Цель работы: исследование свойств непараметрической оценки ин-
версной регрессии.
dxyxfxyXM )|(}|{
∫
∞
∞−
=

42
Далее в тех же условиях и по той же схеме как описано в пункте 6.2
для прямой регрессии выполните исследование для инверсной регрессии.
6.4 Исследование правила классификации в распознавании обра-
зов с использованием непараметрической реализации байесовского под-
хода
При тех же условиях, что описаны в пункте 4.1, считая, что функции
плотности неизвестны реализуйте и исследуйте непараметрическую реализа-
цию байесовского подхода:
При байесовском подходе к принятию решений решающая функция
имеет вид:
)
2
(
)
2
|
(
)
1
(
)
1
|
(
)
(
P
x
f
P
x
f
x
−
=
η
По обучающей выборке находим непараметрические оценки условных
плотностей
)
1
|
(
x
f
и априорных вероятностей
)
1
(
P
:
5/1
,
11
)|(
ˆ
−
∈
=
−
=
∑
cnh
h
xx
K
hn
lxf
l
n
Ii
i
l
, 2,1,)(
ˆ
== l
n
n
lP
l
.
Получаем непараметрическую оценку решающей функции:
=
−
−
−
=η
∑∑
∈∈
n
n
h
xx
K
hnn
n
h
xx
K
hn
x
nn
Ii
i
Ii
i
n
2
2
1
1
2
1
1111
)(
)
i
n
i
i
y
h
xx
K
hn
∑
=
−
=
1
11
Как видно из структуры обучающего правила можно (и нужно) подоб-
рать оптимальные ядра и коэффициенты размытости для обеспечения мини-
мума ошибки классификации.
При минимизации оценки вероятности ошибки по параметрам
c
коэф-
фициентов размытости
h
надо учесть, что зависимость
).о( шP
n
′
от
c
раз-
рывная. Для оптимизации необходимо использовать квазиградиентные алго-
ритмы, в которых вместо градиентов от
n
P
′
по
c
используются их оценки
(квазиградиенты). Можно применить метод глобальной оптимизации, опи-
санный в главе 5 учебного пособия.
Полученный классификатор необходимо исследовать на зависимость
от:
1. Объема обучающей выборки.

43
2. Априорных вероятностей классов.
3. Типов ядер.
4. Коэффициентов размытости ядер.
По результатам тестирования построить необходимые графики.
Если ранее выполнялась работа из пункта 4.1, то произвести сравнение
параметрического и непараметрического подходов, проиллюстрировав пове-
дением при одних и тех же начальных условиях.

44
7. МЕТОДЫ ЭКСПЕРИМЕНТАЛЬНОЙ ОПТИМИЗАЦИИ
7.1 Исследование алгоритмов одномерного поиска минимума уни-
модальных функций (деление отрезка пополам и по золотому сечению)
Цель работы: реализовать и сравнить между собой два самых извест-
ных алгоритма одномерной локальной экспериментальной оптимизации.
Произвести тестирование методов на следующем наборе функций:
•
xxxI /16)(
2
+=
при
1
5
≤
≤
x
.
•
xxxI /162)(
2
+=
при
1
5
≤
≤
x
.
•
x
x
x
I
/
1
)
(
+
=
при
1
3
≤
≤
x
.
•
x
x
x
I
/
4
)
(
+
=
при
1
4
≤
≤
x
.
•
2
)2()( −= xxI при
1
4
≤
≤
x
.
•
|
2
|
)
(
−
=
x
x
I
при
1
4
≤
≤
x
.
• Две тестовые функции реализованные самостоятельно.
Входные параметры: выбранная тестовая функция, желаемая точность
решения.
После проведения оптимизации методами деления отрезка пополам и
золотого сечения – сравнить количество вычислений функции произведен-
ных обоими методами.
Для демонстрации – выводить на экран графики тестовых функций.
Подробное описание метода можно найти в учебном пособии в пятой
главе или в любой другой популярной литературе посвященной оптимиза-
ции.
7.3 Исследование симплексного алгоритма поиска экстремума
функций
Цель работы: реализовать и протестировать симплекс метод поиска
экстремума.
Произвести тестирование метода на следующем наборе функций:
•
Ix x bx x x x b( , ) | | | |,
1 2 1 2 1 2
0 1
=
+
+
−
<
<
.
45
•
)1|2|()1|1(|),(
2121
+
−
⋅
+
−
=
xxxxI
.
• 2||,),(
21
2
2
2
121
<µµ++= xxxxxxI .
•
1||,||||),(
212121
≤
µ
µ
+
+
=
xxxxxxI
.
• Две тестовые функции реализованные самостоятельно.
Правильный симплекс – это регулярный многогранник в
R
m
с (
m
+
1
)
вершинами. В двумерном пространстве правильный (регулярный) симплекс
представляет собой равносторонний треугольник, в трехмерном – тетраэдр.
Остановимся на одном из способов построения правильного симплекса.
Вначале построим симплекс, одна из вершин которого находится в на-
чале координат. Координаты вершин определяются матрицей:
( )y
y y y
y y y
y y y
y y y
gg gg
gg g g
gg g g
gg g g
gg g g
y
y
y
j
i
m
m
m m
m
m
m m
m
m
m
=
=
=
+ + +
+
1
1
2
1 1
1
2
2
2 2
1 2
1
1
2
1 1
1
1
1
1
1
2
1
00 00
K
K
K K KK
K
K
K
K
K
K
K
K
K
g
r
m
m m g
r
m
m
1
2
1 1
2
1 1= + −+ = +−( ); ( )
,
в каждой строке которой расположены координаты соответствующей
вершины. Ребро симплекса равно
r
.
Для
m
r
=
=
1
1
,
симплексом является отрезок с координатами 0; 1.
Для
m
r
=
=
2
1
,
симплексом является правильный треугольник с ко-
ординатами вершин (0; 0), (0.96; 0.26), (0.26; 0.96).
Симплекс можно из начала координат переместить в любую выбран-
ную точку
),,,(
11
2
1
1
1
m
xxxx
K
=
пространства:
( )x
x x x
x x x
x x x
x x x
y x
y x
y x
y x
j
i
m
m
m m
m
m
m m
m
m
m
m
=
=
+
+
+
+
+ + + +
1
1
2
1 1
1
2
2
2 2
1 2
1
1
2
1 1
1 1
2 1
1
1 1
K
K
K K KK
K
K
KKK
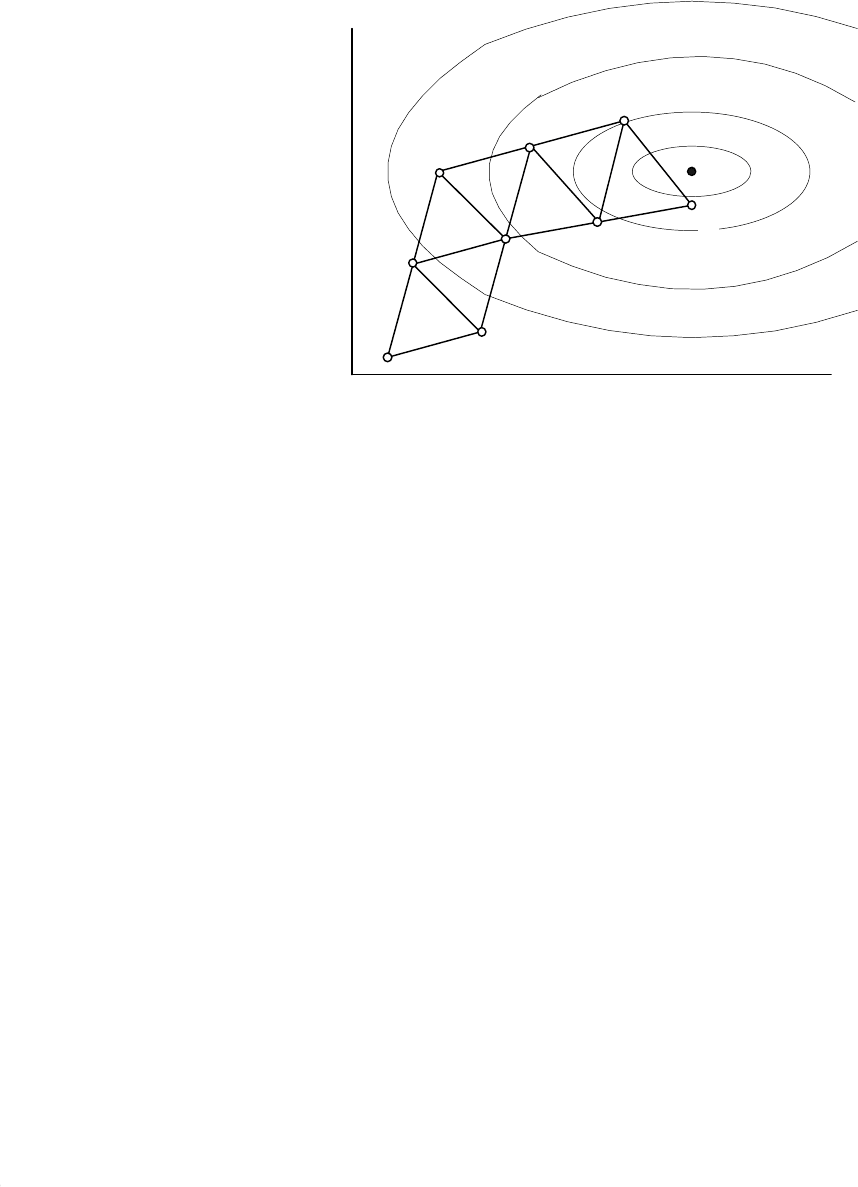
46
После вычисления (или измерения) в вершинах симплекса целевой
функции находим ее максимальное значение. Допустим,
I
x
(
)
максимальна в
вершине 1 (см. рис. 7.1). Вершину 1 отражаем через центр противоположной
грани и получаем симплекс с вершинами 2, 3, 4. В вершине 4 вычисляем
I
x
(
)
. Дальнейшие шаги повторяются.
x
1
x
2
Рисунок 7.1
const
)
(
=
x
I
1
2
3
4
5
6
7
8
9
Как видно из рисунка симплекс «катится» по поверхности функции.
Поиск завершается, когда размеры симплекса становятся достаточно
малы.
7.4 Исследование градиентного алгоритма поиска экстремума
функций (с использованием планирования первого порядка)
Цель работы: реализовать и протестировать градиентный алгоритм по-
иска экстремума с использованием планирования первого порядка.
Реализовать метод поиска и произвести его тестирование на тех же тес-
товых функциях как в пункте 7.3.
Простейший градиентный алгоритм поиска минимума функции имеет
вид:
0,,2,1,0),(
1
>γ=∇γ−=
+ lllll
lxIxx
K
)
.
Оценка составляющих градиента вычисляется за счет обработки экспе-
риментальных данных (значений минимизируемой функции в точках плана),
47
полученных с использованием ортогонального планирования первого поряд-
ка. В результате планирования и обработки его результатов находим пара-
метры
m
β
β
β
,,,
21
K
, которые являются оценками градиента в безразмерных
координатах. При переходе к размерным координатам составляющие гради-
енты принимают вид:
m
m
m
xxx ∆
β
=α
∆
β
=α
∆
β
=α ,,,
2
2
2
1
1
1
K
Например, для двумерного случая имеем:
∆
β
∆
β
=
∂
∂
∂
∂
=∇
2
2
1
1
2
1
)(
)(
)(
x
x
x
xI
x
xI
xI
l
l
l
)
)
)
где
21
,
β
β
– коэффициенты линейной модели в безмерных координатах;
21
, xx
∆
∆
– интервалы покачивания координат относительно точки
),(
21
ll
xx
;
γ
– величина шага.
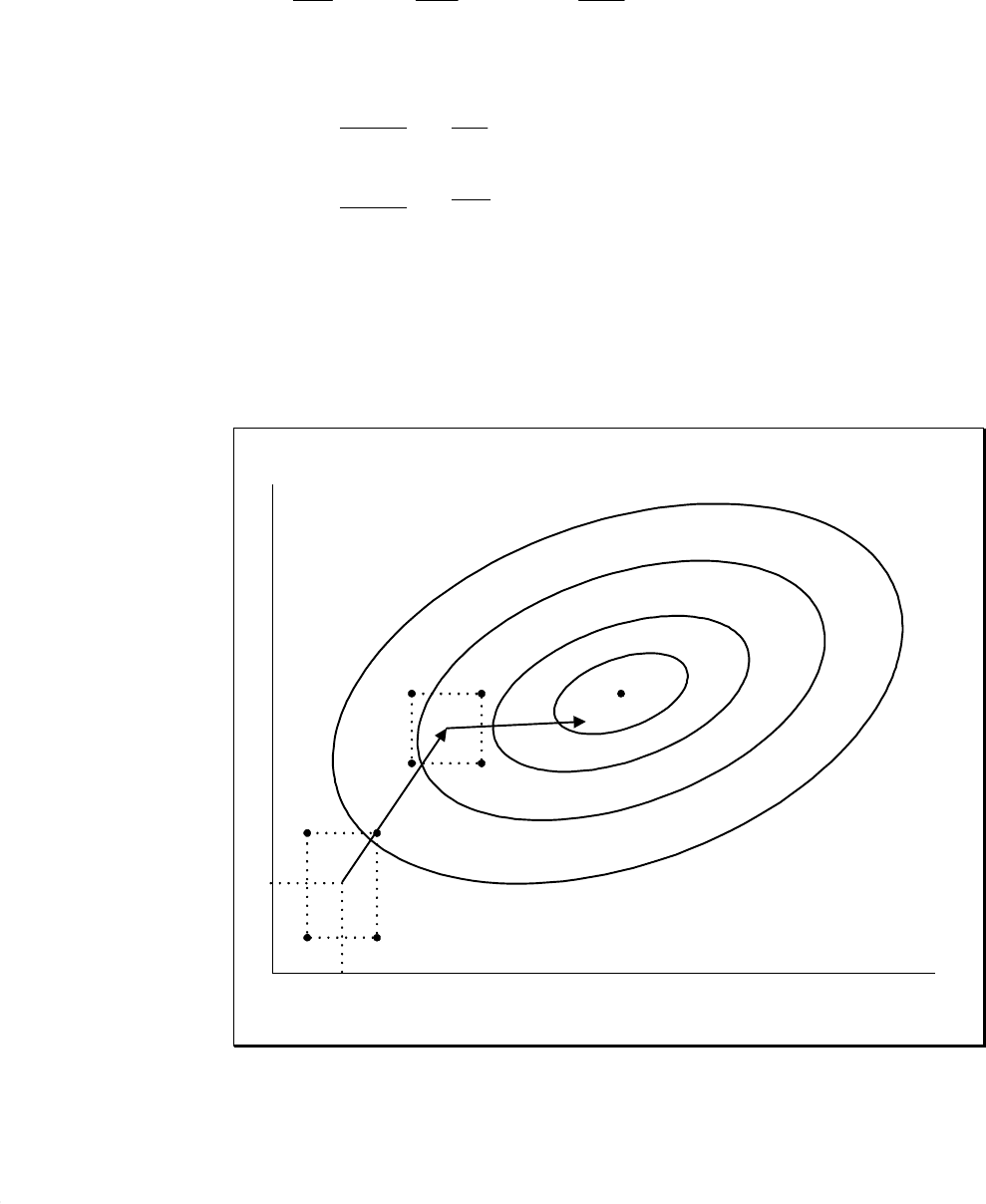
Примерное поведение алгоритма приведено на рисунке 7.2.:
Рисунок 7.2
x
1
x
2
x
l
1
x
l
2

48
Поиск завершается когда очередное значение функции качества мало
отличается от предыдущего шага.
Если выполнялась работа из пункта 7.3, то произвести сравнение этого
алгоритма с симплекс методом по количеству вычислений функции качества.
7.5 Исследование алгоритма Ньютона поиска экстремума функций
(с использованием планирования второго порядка)
Цель работы: реализовать и протестировать градиентный алгоритм по-
иска экстремума с использованием планирования второго порядка.
Реализовать метод поиска и произвести его тестирование на тех же тес-
товых функциях как в пункте 7.3.
Один из простых вариантов алгоритма Ньютона имеет вид:
K
)
)
,2,1,0),(
)(
1
2
1
=∇
∂∂
∂
−=
−
+
lxI
xx
xI
xx
l
l
ll
Для расчета оценок градиента и матрицы вторых производных осуще-
ствим ортогональное композиционное планирование второго порядка. После
обработки измеренных (вычисленных) в точках плана значений минимизи-
руемой функции получаем параметры безразмерной модели (при
m
=
2
):
1
β
,
2
β
,
11
β
,
2112
β
=
β
,
22
β
.
По этим коэффициентам вычисляем элементы матриц:
∆∆
β
∆∆
β
∆∆
β
∆∆
β
=
∂∂
∂
∆
β
∆
β
=∇
22
22
21
12
21
12
11
11
2
2
1
1
1
2
2
)(
,)(
xxxx
xxxx
xx
xI
x
x
xI
l
l
)
)
На рисунке. 7.3 приведен один шаг, выполненный в соответствии с ал-
горитмом Ньютона. Если функция
I
x
(
)
хорошо аппроксимируется уравне-
нием второго порядка, то алгоритм Ньютона за один шаг обеспечивает выход
в окрестность минимума.
49
∗
∗
∗
∗
Рисунок 7.3
x
1
x
2
Поиск завершается когда очередное значение функции качества мало
отличается от предыдущего шага.
Если выполнялась работа из пункта 7.3, то произвести сравнение этого
алгоритма с симплекс методом по количеству вычислений функции качества.
Если выполнялась работа из пункта 7.4, то произвести сравнение этого
алгоритма с алгоритм поиска экстремума с использованием планирования
первого порядка по количеству вычислений функции качества.

50
8. ИДЕНТИФИКАЦИЯ СТАТИЧЕСКИХ МОДЕЛЕЙ
ОБЪЕКТОВ
8.1 Исследование алгоритма наименьших квадратов при линейной
параметризации модели
Цель работы: исследование свойств алгоритма расчета параметров ос-
нованного на методе наименьших квадратов при линейной параметризации
модели.
Входные параметры: структура линейного объекта, свойства помехи
приложенной к выходу объекта (нормально распределенная величина с нуле-
вым математическим ожиданием и некоторой дисперсией помехи).
Модель объекта задана в виде линейной комбинации известных (базис-
ных) функций
)(...,),(
1
uu
m
ϕ
ϕ
:
∑
=
ϕα=αϕ=αϕ=αη
m
j
TT
jj
uuuu
1
)()()(),( ,
ϕ
ϕ
=ϕ
α
α
=α
)(
)(
)(,
11
u
u
u
mm
KK .
Вектор-столбец значений выхода модели (в моменты времени
n
i
,
,
1
K
=
) имеет вид:
αΦ=α
ϕϕϕ
ϕϕϕ
=α
ϕ
ϕ
=
αϕ
αϕ
=α
)()()(
)()()(
)(
)(
)(
)(
)(
21
11211
11
nmnn
m
n
T
T
n
T
T
uuu
uuu
u
u
u
u
H
K
K
K
KK .
Параметры
α
находим по критерию наименьших квадратов
α
−−
=αΦ−αΦ−=α min)()()(
*1*
HKHI
T
Необходимое условие минимума
∇
=
I
0
(где
∇
I
– градиент от
)
(
α
I
по
α
) приводит к системе линейных алгебраических уравнений:
*11
H
K
K
TT −−
Φ
=
α
Φ
Φ
,
которая имеет единственное решение, если матрица
Φ
Φ
T
K
−1
невыро-
ждена. Эта матрица вырождается, если: 1) либо базисные функции линейно
зависимы, 2) либо число изменений
n
меньше числа
m
искомых параметров
