Рубан А.И. Методы анализа данных. Практикум
Подождите немного. Документ загружается.

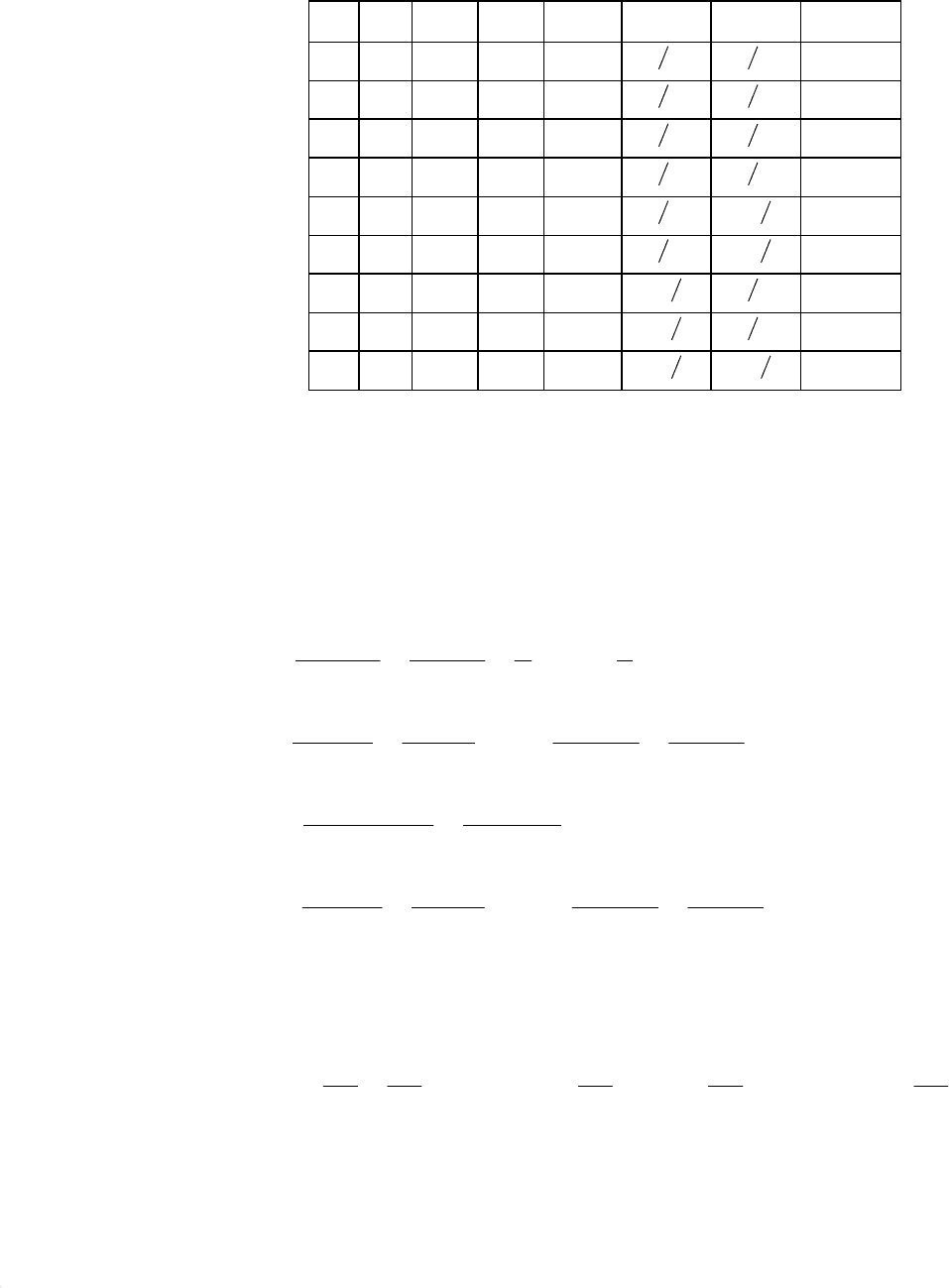
31
1
0
11
uuu ∆+=
,
0
22
uu =
. Реализуем эти значения входов на объекте и измеря-
ем значение выходной переменной
5
y .
Таблица 5.3
n
x
0
1
x
2
x
21
xx
1
x
′
2
x
′
y
1 + + + +
31
31
1
y
2 + – + –
31
31
2
y
3 + + – –
31
31
3
y
4 + – – +
31
31
4
y
5 + + 0 0
31
32
−
5
y
6 + – 0 0
31
32
−
6
y
7 + 0 + 0
32
−
31
7
y
8 + 0 – 0
32
−
31
8
y
9 + 0 0 0
32
−
32
−
9
y
Параметры
221112210
,,,,,
β
β
β
β
β
β
′
в силу ортогональности плана вы-
числяются независимо (так же как и при использовании ортогонального пла-
на первого порядка):
∑
=
β
−
=
′
β−
′
β−β−β−β−β
′
−σ=
n
i
iy
xxxxxxyI
1
2
22111211222110
2
min)(
∑∑
==
====β
′
9
11
0
00
0
0
9
11),(
),(
),(
i
i
n
i
i
yy
nn
yx
xx
yx
,
6
),(
),(
),(
1
11
1
1
yx
xx
yx
==β ,
6
),(
),(
),(
2
22
2
2
yx
xx
yx
==β ,
4
),(
),(
),(
21
2121
21
12
yxx
xxxx
yxx
==β ,
2
),(
),(
),(
1
11
1
11
yx
xx
yx
′
=
′′
′
=β ,
2
),(
),(
),(
2
22
2
22
yx
xx
yx
′
=
′′
′
=β .
Параметры некоррелированные и дисперсии их различны:
9
22
2
0
yy
n
σ
=
σ
=σ
β
′
,
6
2
22
21
y
σ
=σ=σ
ββ
,
4
2
2
12
y
σ
=σ
β
,
2
2
22
2211
y
σ
=σ=σ
ββ
.

32
В заключение остается пересчитать коэффициент
3
2
3
2
22110
2
222
2
11100
β−β−β
′
=β−β−β
′
=β xx ,
который оценивает сигнальную часть выхода объекта в центре плана.
В итоге построена модель второго порядка:
=β+β+β+β+β+β=
2
222
2
111211222110
xxxxxxy
)
+−α+−α+α= )()(
0
222
0
1110
uuuu
20
2222
20
1111
0
22
0
1112
)()())(( uuuuuuuu −α+−α+−−α+
00
β
=
α
,
1
1
1
u∆
β
=α
,
2
2
2
u∆
β
=α
,
21
12
12
uu ∆∆
β
=α
,
2
1
11
11
)( u∆
β
=α
,
2
2
22
22
)( u∆
β
=α
.
Адекватность модели проверяется по той же схеме, как и для линей-
ной модели. Соответствующие формулы выпишите самостоятельно.
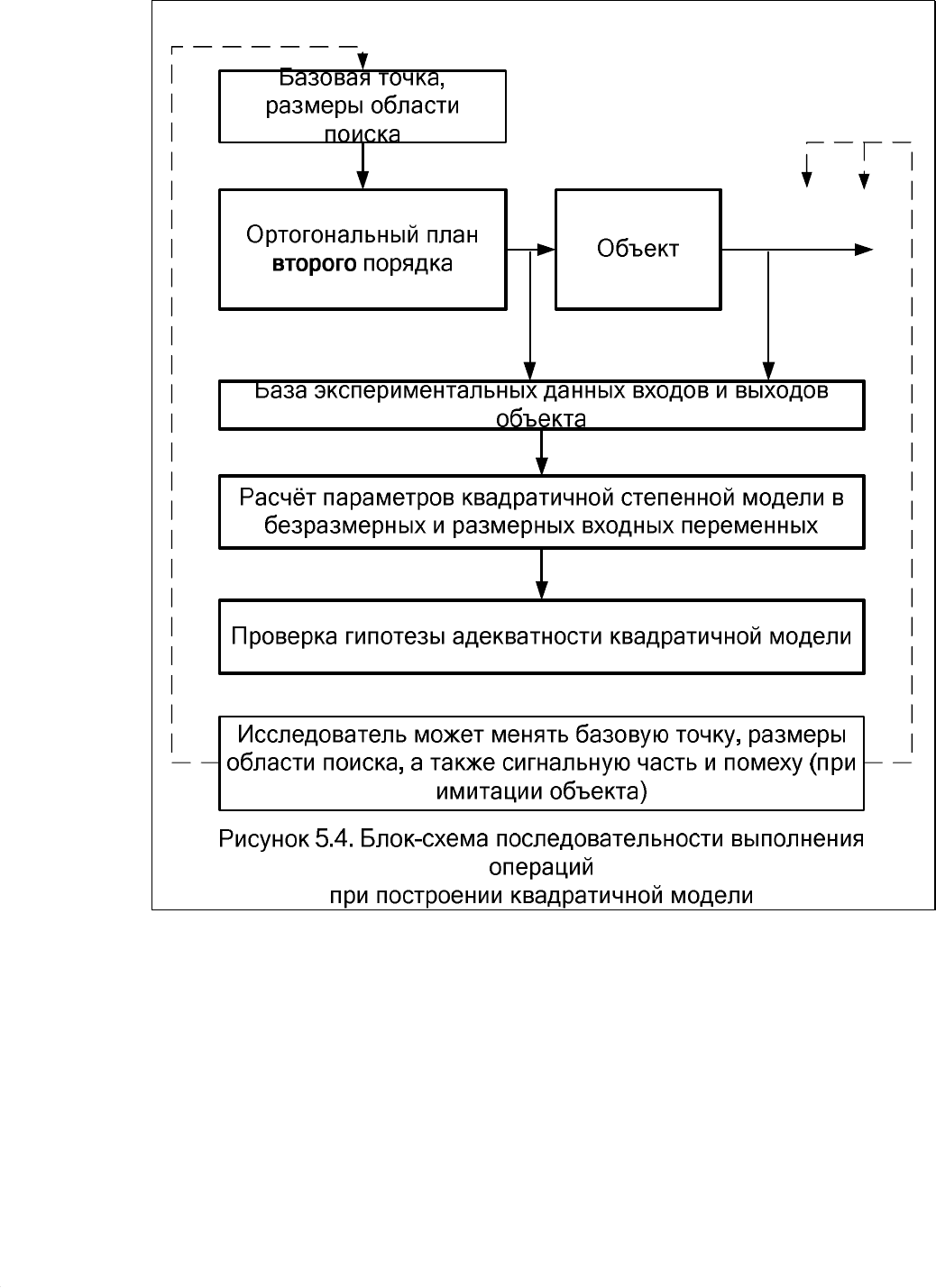
Блок схема последовательности выполнения операций при построении
квадратичной модели приведена на рис. 5.4.
33
При исследовании алгоритмов построения моделей естественно ис-
пользуется имитация объекта.
На рисунке 5.5 приведена блок-схема последовательности выполнения
операций при имитации объекта.
Интенсивность помехи берётся по отношению к интенсивности сиг-
нальной части. Показатели интенсивности и относительную величину интен-
h
u
y
+
ϕ
=
)
(

34
сивностей Вы должны выбрать самостоятельно и использовать при установ-
лении соответствующих закономерностей.
2
2
2
1
)( uuu +=ϕ
huuy ++=
2
2
2
1
Приведённые ранее блок-схемы помогут Вам составить и выполнять
план исследований.

35
6. МЕТОДЫ НЕПАРАМЕТРИЧЕСКОЙ ОБРАБОТКИ
ИНФОРМАЦИИ
6.1 Исследование оценок "К ближайших соседей" и Розенблатта –
Парзена
Цель работы: исследование свойств непараметрических оценок "К
ближайших соседей" и Розенблатта – Парзена.
Входные данные: случайная величина, распределенная по некоторому
закону распределения (задается во время работы программы), параметры
случайной величины (зависят от выбранного закона), объем выборки
n
и па-
раметры оценок (для оценки "К ближайших соседей" это
k
– количество
ближайших «соседей», а для оценки Розенблатта – Парзена это коэффициент
размытости
h
и вид ядра).
Оценка по методу "К ближайших соседей" имеет вид:
),,(2
1
)(
xnkn
k
xf
n
n
n
ρ
−
=
Оценка Розенблатта – Парзена имеет вид:
−
=
∑
=
h
xx
K
hn
xf
i
n
i
n
1
11
)(
Для исследования необходимо ввести параметры моделируемой слу-
чайной величины, сгенерировать выборку объема
n
(рекомендуемый объем
30
≥
n
). Ввести параметры для оценок.
Затем построить график на котором будут изображены точки выборки
и график выбранной оценки.
Произвести анализ зависимости оценок от своих параметров и от объе-
ма выборки.
Определить наилучший вид ядра для оценки Розенблатта – Парзена.
Произвести сравнение оценок между собой.
36
Проверить работу оценок при больших объемах выборки (
1000
≥
n
).
Исследовать, как зависит оценка Розенблатта – Парзена от коэффици-
ента размытости с ростом объема выборки.
6.2 Исследование непараметрической оценки прямой регрессии
Цель работы: исследование свойств непараметрической оценки прямой
регрессии (между выходом и выходом объекта).
Регрессией называют первый начальный условный момент:
)()|(}|{ xdyxyfyxYM η==
∫
∞
∞−
.
Это одна из простейших усредненных количественных зависимостей
между выходом
Y
и входом
X
объекта.
X
и
Y
– это непрерывные изме-
ряемые случайные величины.
Оценка )(x
n
η
регрессии строится на основе серии измерений выхода и
входа объекта:
xy i n
i i
, , ,=1
:
∑
=
−
=η≡
n
i
i
i
Nn
y
h
xx
KxxYM
1
)(}|{
)
,
∑
=
−
−
=
−
n
j
j
i
i
N
h
xx
K
h
xx
K
h
xx
K
1
.
Колоколообразная функция
−
h
xx
K
i
N
по форме повторяет ядро
K
(
)
⋅
и отличается от него на нормирующий множитель
∑
=
−
n
j
j
h
xx
K
1
/1
. За счет
этого
∑
=
=
−
n
i
i
N
h
xx
K
1
1, т. е. ядро
−
h
xx
K
i
N
нормировано на 1 на системе
экспериментальных точек.
Нормированность ядер
−
h
xx
K
i
N
приводит к условию:

37
},1,max{)(},1,min{ niyxniy
i
n
i
=≤η≤= ,
которое говорит о существовании полосы, за пределы которой не вы-
ходит непараметрическая оценка регрессии.
Ядра
K
z
(
)
колоколообразные усечённые нормированные. Это факти-
чески некоторые плотности распределения вероятности. Примеры прямо-
угольного, треугольного, параболического и кубического ядер приведены
ниже:
<
≤
=
.||1,0
,1||,5.0
)(
z
z
zK
<
≤
−
=
|;|1,0
,1|||,|1
)(
z
zz
zK
<
≤−
=
|;|1,0
,1||),1(75.0
)(
2
z
zz
zK
<
≤−+
=
.||1,0
,1||,|)|1|)(|21(
)(
2
z
zzz
zK
Усечённость нормированных ядер )(
⋅
N
K (в силу усечённости ядра
K
(
)
⋅
) позволяет при построении оценки
)(x
n
η
в каждой фиксированной
точке
x
учитывать только несколько близлежащих значений
x
i
и не "пере-
лопачивать" всю выборку.
Выбор оптимальной формы ядра
K
(
)
⋅
и коэффициента размытости
h
(
)
⋅
решается так же как и для оценок плотностей. Записывается квадратич-
ный критерий оптимальности:
hK
n
dxxxMhKI
,
2
min})]()({[),( =η−η=
∫
∞
∞−
и из него отыскивается решение:
≤
≤−
=
,||1,0
,1||),1(75.0
)(
2
z
zz
zK
.0,)(
5/1
ccnnh ≤=
−
Функция качества
)
,
(
h
K
I
от формы усеченных "колоколообразных"
ядер
K
(
)
⋅
зависит слабо. Основное влияние оказывает положительная кон-
станта
c
, но зависимость
I
от
c
при возрастании
n
ослабевает. Форма ядра

38
усеченная параболическая. Константа
c
, определяющая коэффициент размы-
тости, вычисляется по выборке путём минимизации эмпирических показате-
лей (характеризующих наилучшее сглаживание экспериментальных данных).
Считаем, что выборке
niyx
ii
,1),,( =
измерениях входа находятся на
равных расстояниях друг от друга
∆
=
−
=
−
+
x xi n
i i1
1 1( , ), а объем выборки
n
фиксирован. Перейдем от размерного параметра
c
(его размерность, об-
ратная размерности
x
) к безразмерному
β
:
5/11
nc ∆=β
−
.
Оценка регрессии приобретает вид:
∑
=
∆
−
β=η≡
n
i
i
i
Nn
y
xx
KxxYM
1
)(}|{
)
∑
=
∆
−
β
∆
−
β
=
∆
−
β
n
j
j
i
i
N
xx
K
xx
K
xx
K
1
Интервал изменения коэффициента
β
:
1
0
≤
β
≤
.
При
0
=
β
оценка регрессии
)(x
n
η
не зависит от
x
. Такой вариант, хо-
тя и редко, но возможен. Выбранный вход объекта не оказывает влияния на
выход объекта.
При
1
=
β
оценка регрессии
)(x
n
η
точно проходит через эксперимен-
тальные точки, т. е. оценка не осуществляет сглаживания экспериментальных
дынных. Такой вариант тоже возможен, если сигнальная часть выхода объек-
та не зашумлена помехой.
При наличии помех в выходе объекта оценка должна сглаживать экс-
периментальные дынные. Этот наиболее распространённый вариант соответ-
ствует параметру
β
, находящемуся внутри интервала [0; 1]. Для его вычис-
ления необходимо строить критерии оптимальности.
Среди возможных критериев оптимальности непараметрической оцен-
ки регрессии (что эквивалентно оптимальности параметра
β
) приближенны-
ми к реальным ситуациям являются два из них.
Один критерий основан на использовании "скользящего экзамена":
39
∑
=
β
=η−=
n
i
inin
xy
n
I
1
2
1
min))((
1
,
∑
≠
=
−
=η
n
k
k
ki
Nin
ik
y
h
xx
Kx
1
)(
Выборка
xy i n
i i
, ( ,)
=
1
при этом своеобразно разбивается на две час-
ти: одна используется для построения модернизированной модели
)(x
n
η
,
вторая – для ее проверки (по вышеуказанному критерию). Первое слагаемое
в
n
I
1
(т. е. при
i
=
1
) равно квадрату невязки между выходом объекта
y
1
и
выходом модели
)(
1
x
n
η
в первой экзаменующей точке
( , )x y
1 1
. Эта экзаме-
нующая точка не участвует в построении (в обучении) модели
)(
1
x
n
η
. Затем
берется вторая экзаменующая точка
( , )x y
2 2
и в ней вычисляется квадрат не-
вязки между выходами объекта
y
2
и модели
)(
2
x
n
η
, где модель
)(
2
x
n
η
по-
строена по всей выборке кроме точки
( , )x y
2 2
, и т. д. Функция качества
n
I
1
имеет относительно параметра
β
хорошо выраженный минимум. У этого
критерия есть свои особенности.
При
15.0
<
β
≤
оценка
)(
in
x
η
остается постоянной:
2/)()(
11 +−
+
=
η
iiin
yyx
,
т. е. независящей от
β
. Следовательно, функция каче-
ства
n
I
1
перестает зависеть от
β
. Если оптимальное значе-
ние (по другому критерию) параметра
β
находится в интер-
вале [0.5; 1.0], то минимизацией функции качества
n
I
1
мы
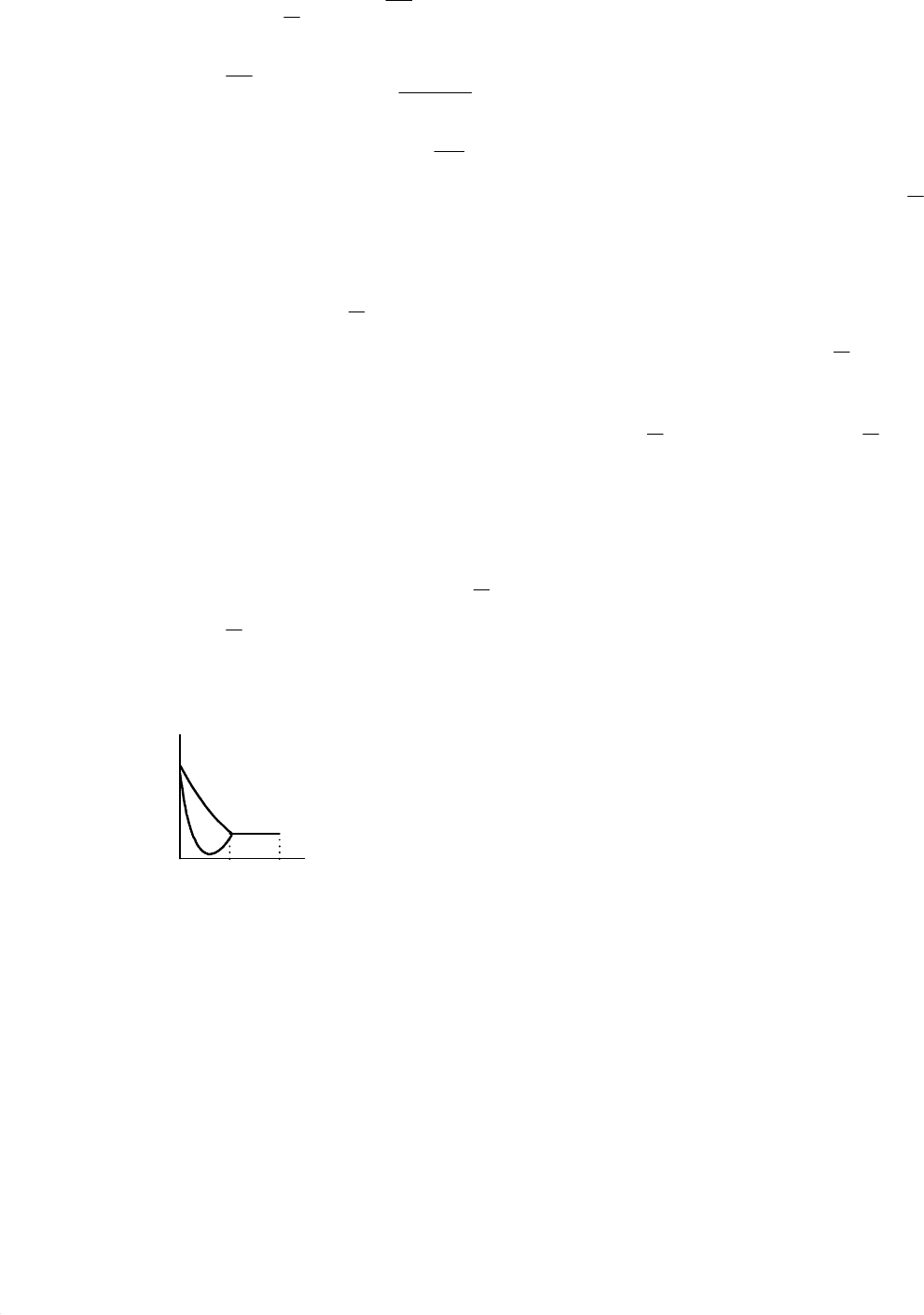
его не найдем (см. кривую 1 на рисунке 6.1). Второй вари-
ант (кривая 2 рисунке 6.1) соответствует более лучшей си-
туации, когда
0
β лежит внутри допустимого интервала
5.00
≤
β
≤
.
Второй показатель качества основан на прямом разбиении выборки на
две части:
xyi M xyi M
i i n i i n
, , , , ,
∈
∈
1 2
.
По одной из них (объема
n
1
) строится оценка регрессии, по второй
(объема
n
2
) – показатель качества:
Рисунок 6.1
β
n
I
1
1
2
0 0.5 1.0

40
(
)
10
2
2
3
min)(
1
2
12
≤β≤
∈
=η−=
∑
n
Ml
lnin
xy
n
I
∑
∈
∆
−
β=η
1
1
)(
n
Mi
i
i
Nn
y
xx
Kx .
При наличии одного входа разбиение на множества
M M
n n
1 2
,
можно
выполнить сравнительно легко. Надо упорядочить выборку
xyi n
i i
, , ,
=
1
по
x
, т. е. сделать в выборке все
1+
<
ii
xx
. Затем выборочные точки с нечетными
номерами отнести к первой группе, с четными номерами – ко второй группе.
После настройки параметра
β
оценка регрессии
)(x
n
η
(при дальнейшем её
использовании) строится по всей выборке.
Для поиска параметра
β
в одномерном случае хорошо подходят: метод
деления отрезка пополам и метод золотого сечения (см. раздел 6 учебного
пособия). Алгоритмы просты в реализации, имеют высокую скорость сходи-
мости, не требуют дифференцирования функции качества и хорошо описаны
во всех учебниках по методам оптимизации.
Если оценка )(x
n
η
для одного и того же канала вход-выход применя-
ется многократно с изменением объема
n
выборки, то можно при фиксиро-
ванном
n
рассчитать
β
, затем пересчитать постоянный для этого объекта па-
раметр
c
и получать оценку
)(x
n
η
по вышеприведённой формуле (при
5/1
)(
−
=cnnh
) для других значений
n
.
Блок-схема последовательности выполнения операций при построении
непараметрической оценки регрессии приведена на рис. 6.2. Там же приведе-
ны варьируемые переменные, которые помогут Вам при составлении плана
исследований.
