Рубан А.И. Методы анализа данных. Практикум
Подождите немного. Документ загружается.

21
Задаются исследователем
структуры условных
плотностей классификатора
с точностью до параметров
Доопределяются параметры
условных плотностей и
априорные вероятности:
Строится байесовское решающее правило:
)2(
ˆ
)
ˆ
,2|,()1(
ˆ
)
ˆ
,1|,(),(
ˆ
где
истинный, 2 класс то,0),(
ˆ
если
истинный, 1 класс то,0),(
ˆ
если
22112121
21
21
PxxfPxxfxx
xx
xx
θ−θ=η
<η
>
η
rr
.2,1),,|,(
21
=θ jjxxf
j
r
Задаются исследователем
статистические характеристики
объекта:
Формируется обучающая
выборка объёма n :
.2,1),(
классов ивероятност априорные
,2,1,
плотностей уусловныхпараметры
,2,1),,|,(
плотностей
условных
структура
21
=
=θ
=θ
jjP
j
jjxxf
j
j
r
r
)2(
ˆ
),1(
ˆ
,
ˆ
,
ˆ
21
PPθθ
r
r
Исследователь может менять
Вычисляется показатель качества работы классификатора:
Рисунок 4.1. Блок-схема последовательности выполнения операций
.
2
класс
является
истиннымкогда ,,,,
1, класс является
истиннымкогда ,,,,
)2()2(
2
)2(
1
)1()1(
2
)1(
1
2
1
n
n
xxx
xxx
r
K
rr
r
K
r
r
:,
21
θθ
r
r
n
n
P
ош
ош
ˆ
=
22
4.2 Исследование байесовского правила классификации в распо-
знавании образов при непрерывных информативных признаках (услов-
ные плотности известны с точностью до параметров) и без обучающей
выборки.
Цель работы: исследование решающего правила классификации при
условиях:
• Имеется два независимых непрерывных информативных призна-
ка
21
, XX и неизвестно сколько классов;
• Априорные вероятности классов неизвестны;
• Все условные плотности вероятности (при условии истинности
того или иного класса) для информативных признаков одинаковы
и известны с точностью до параметров
K
r
r
r
,1),,(
21
=θθ=θ j
jjj
:
K
r
r
r
,1),,|(),|(),|,(
221121
=θθ≡θ jjxfjxfjxxf
jjj
;
• обучающая выборка неизвестна. Имеется обыкновенная выборка
объёма
n
.
Как видно из условий задача очень похожа на уже рассмотренную в
пункте 4.1 задачу, но эта ситуация более сложная и к тому же более распро-
страненная на практике Необходимо построить самообучающуюся систему
классификации.
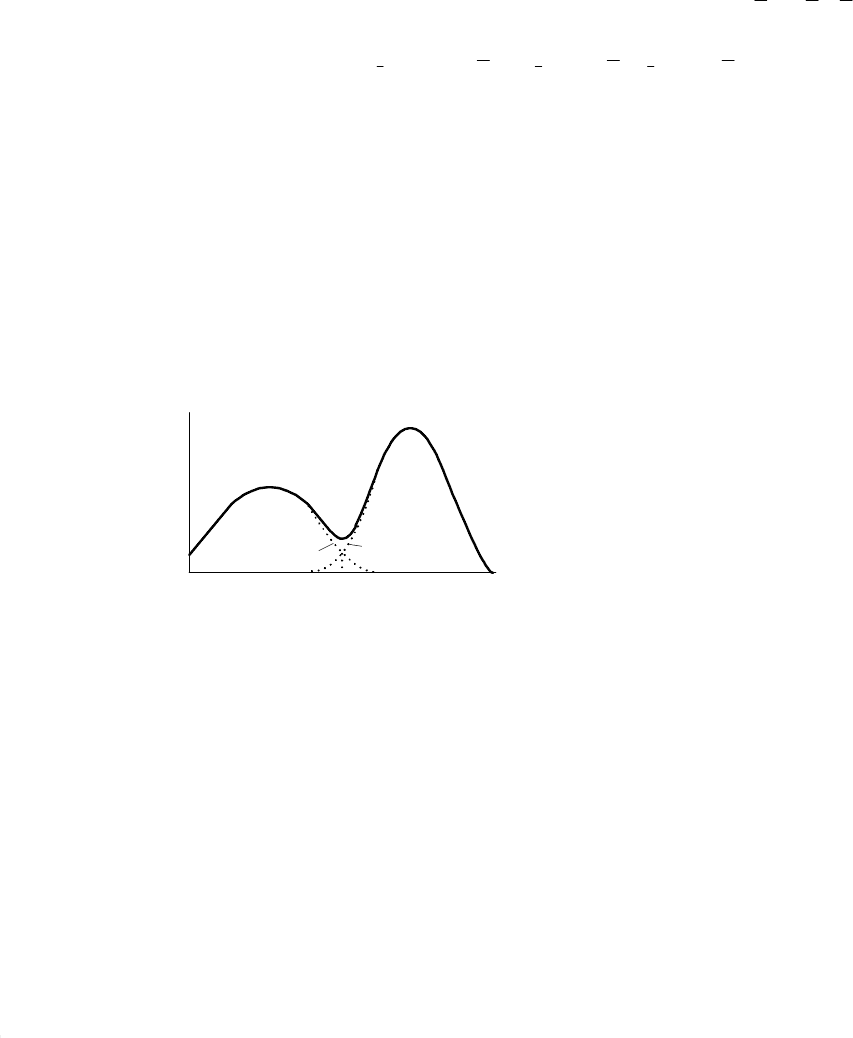
Рассмотрим один из вариантов.
По количеству максимумов мы можем
определить количество классов.
По количеству минимумов и их поло-
жению мы можем определить границы
классов, что позволит произвести разбиение
исходной выборки на две части и тем самым
свести практически свести ситуацию к зада-
че, описанной в пункте 4.1.
Далее строится процедура последовательного (итерационного) расчета
порога (в многомерном случае – разделяющей поверхности)
c
. Например,
задается нулевое приближение порога
c
0
. Оно разбивает исходную выборку
(по которой оценивалась безусловная плотность
f
x
(
)
на две части. Выборка
становится обучающей. По ней (как было рассмотрено выше) оцениваются
условные взвешенные плотности
f
x
P
(
|
)
(
)
1
1
и
f
x
P
(
|
)
(
)
2
2
, а следовательно,
f
x
(
)
x
c
f
x
P
(|)()1 1
f
x
P
(
|
)
(
)
2
2
Рисунок 4.2
23
решающая функция и новое приближение порога
c
1
(разделяющей поверх-
ности) и т. д.
Возможны и другие пути самообучения.
Например для моделирования этой ситуации вы можете взять два клас-
са (
m
= 2), один информативный признак и условные плотности
2
,
1
),
|
(
=
j
j
x
f
, – это нормальные законы распределения:
2
2
2
1
)1|(
x
exf
−
π
=
,
∞<<∞−
π
=
−
−
xexf
x
,
2
1
)2|(
2
)4(
2
.
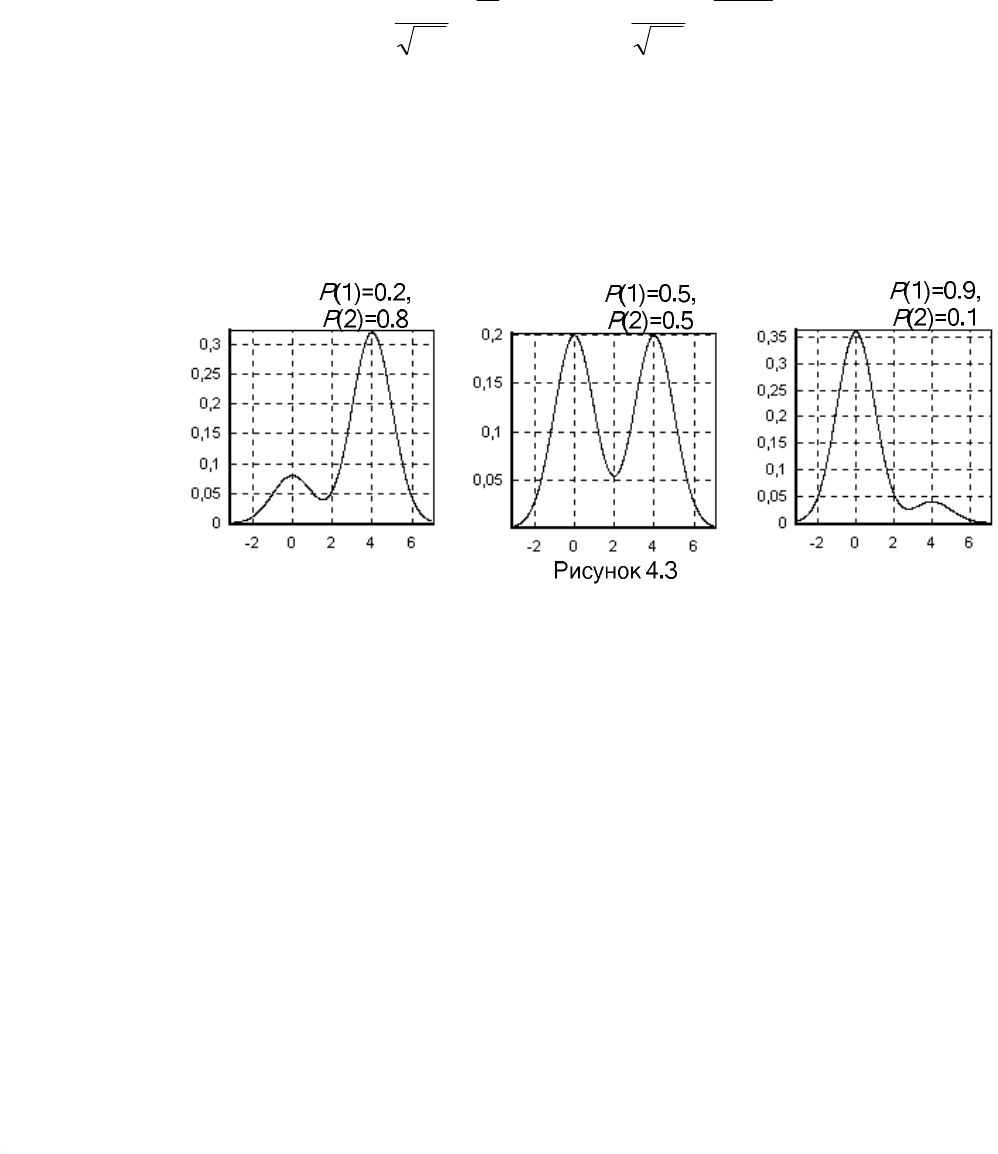
Если законы имеют одинаковую единичную дисперсию и отличаются
математическими ожиданиями:
1
m
= 0,
2
m
= 4, то итоговые плотности рас-
пределения
)
(
x
f
информативного признака
X
при различных значениях ап-
риорных вероятностей классов
)
1
(
P
и
)
2
(
P
приведены на рис. 4.3.
)
(
x
f
)
(
x
f
)
(
x
f
x
x
x
При реализации расчетно-графической работы необходимо варьиро-
вать: количество классов, математические ожидания и априорные вероятно-
сти классов.
Для наглядной демонстрации реализованная программа должна выво-
дить графики похожие на те, что приведены на рисунке 4.3.
24
5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
5.1 Исследование алгоритмов построения степенных моделей с ис-
пользованием ортогональных планов первого и второго порядков
Цель работы: исследование алгоритмов планирования эксперимента
при построении степенных моделей первого и второго порядка.
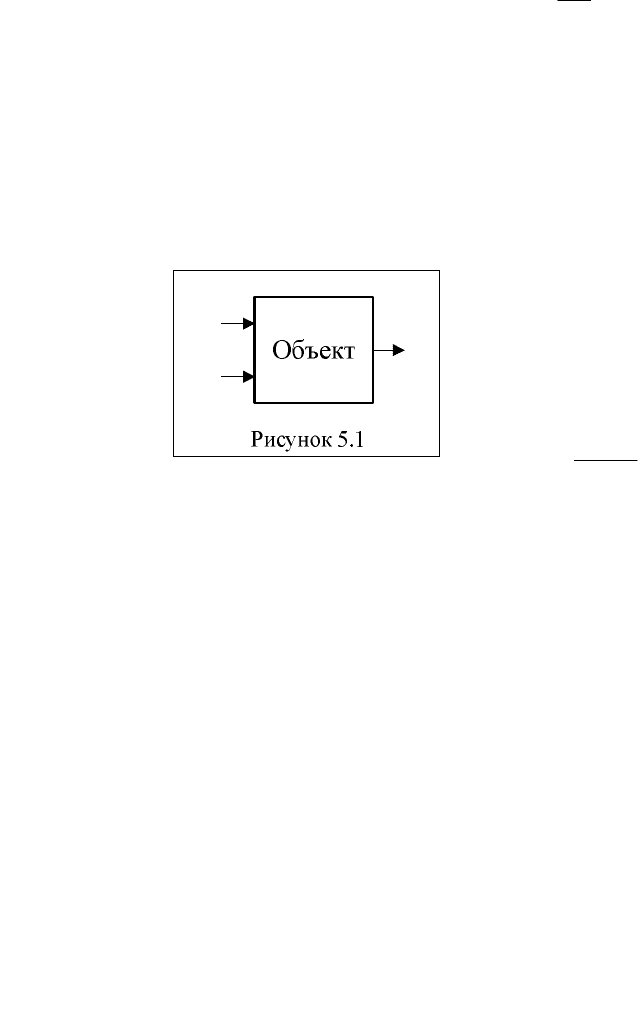
Объект исследования (рисунок. 5.1) имеет два входа
21
, uu и один вы-
ход
y
. Основная проблема планирования эксперимента состоит в создании
таких планов покачивания входных переменных (при снятии эксперимен-
тальных данных [ niyuu
i
i
i
,1),,,(
2
1
= ] с объекта), которые обеспечивают бо-
лее быстрое и точное построение модели объекта. Выход объекта
y
состоит
из неизвестного сигнала (здесь )(
⋅
ϕ
– неизвестная функции от входов, назы-
ваемая поверхностью отклика) и центрированной аддитивной помехи
(
0
)
(
=
h
M
).
huuy
+
ϕ
=
),(
21
Модель первого порядка:
≡−α+−α+α= )()(
ˆ
0
222
0
1110
uuuuy
22110
xx β+β+β≡ ,
2,1,,,
00
0
=∆α=βα=β
∆
−
= ju
u
uu
x
jjj
j
jj
j
Модель второго порядка:
≡−α+−−α+−α+
+−α+−α+α=
20
2222
0
22
0
1112
20
1111
0
222
0
1110
)())(()(
)()(
ˆ
uuuuuuuu
uuuuy
2
2222112
2
11122110
xxxxxx β+β+β+β+β+β≡
,2,1,,
00
=
∆
α
=
β
α
=
β
ju
jjj
222222211212111111
,, uuuuuu
∆
∆
α
=
β
∆
∆
α
=
β
∆
∆
α
=
β
Здесь
),(
0
2
0
1
uu
– базовая точка.
Измерения выхода объекта некоррелированные равноточные.
u
1
2
u
y

25
Расчёт параметров β
r
моделей первого и второго порядков в безразмер-
ных переменных проводится по методу наименьших квадратов.
Построение линейной модели
Итак, модель имеет вид:
22110
0
222
0
1110
)()(
ˆ
xxuuuuy β+β+β≡−α+−α+α=
Необходимо на основе эксперимен-
та: niyuu
i
i
i
,1],,,[
2
1
= ) вычислить ко-
эффициенты
210
,,
α
α
α
модели.
Экспериментальные точки для
входных координат зададим в вершинах
гиперпрямоугольника. Точки такого плана
для
m
=
2
показаны в верхней части рис.
5.2. Эти точки равномерно распределены
относительно известной базовой точки
),(
0
2
0
1
0
uuu =
.
Интервалы покачивания
21
, uu
∆
∆
относительно базовой точки задаются экс-
периментатором, и они определяют об-
ласть изучения объекта. Для этой области и строится линейная модель.
С целью унификации процедур построения планов, исследования их
свойств, расчета параметров и исследования качества модели осуществляется
переход от размерных входных переменных
21
, uu
к безразмерным
21
, xx
:
2,1,
0
=
∆
−
= j
u
uu
x
j
jj
j
.
Точки плана в вершинах прямоугольника (верхняя часть рисунка 4) в
новых координатах оказываются в вершинах квадрата с единичными коор-
динатами (нижняя часть рисунка. 5.2). Центр плана переходит в начало коор-
динат. Полученный план представлен в табл. 5.1. В этом плане кроме безраз-
мерных входных переменных
x
1
,
x
2
введены столбец фиктивной переменной
x
0
и столбец измерений выхода объекта в каждой точке плана. Фиктивный
столбец состоит из +1 и служит для симметрии расчета всех коэффициентов
u
1
u
2
u
2
0
u
1
0
∆
u
2
∆
u
2
∆
u
1
∆
u
1
2
1
3
4
1
3
4
2
1
−
1
−
1
Рисунок 5.2
1
x
2
x
1

26
модели. Для упрощения записи плана единица опускается и указывается
только знак единичной координаты.
В новых безразмерных координатах
21
,xx
линейная модель также сохраняет линейный вид:
2
2
1
1
0
2
2
2
1
1
1
0
xxxuxuy
β
+
β
+
β
≡
∆
α
+
∆
α
+
α
=
)
Из этого уравнения следует алгоритм расчета
коэффициентов }{
j
α
по коэффициентам }{
j
β
:
2,1,,
00
=
∆
β
=αβ=α j
u
j
j
j
Параметры 2,1,,
0
=
β
β
j
j
модели рассчитаем по критерию
наименьших квадратов
∑
=
βββ
−
=β−β−β−σ=
n
i
iy
xxyI
1
,,
2
22110
2
210
min)(
предполагая, что измерения выхода
n
yy ,,
1
K
некоррелированные и
равноточные с дисперсией
2
y
σ
. Из этого критерия следует система линейных
алгебраических уравнений:
[
]
),(),(),(),(
0
2
220110000
2
yxxxxxxx
yy
−
−
σ=β+β+βσ ,
[
]
),(),(),(),(
1
2
221111001
2
yxxxxxxx
yy
−
−
σ=β+β+βσ ,
[
]
),(),(),(),(
2
2
222112002
2
yxxxxxxx
yy
−
−
σ=β+β+βσ .
Здесь 2,1,0,
=
jx
j
– столбцы матрицы планирования, включая фик-
тивный столбец
x
0
, состоящий из "плюс единиц",
y
– столбец измерений
выхода объекта; ( , )x x
k j
и
( ,)x y
k
– скалярные произведения столбцов мат-
рицы планирования:
( , ) , ( ,)xx xx x y xy
k j ki ji
i
n
k ki i
i
n
= =
=
=
∑ ∑
1
1
Таблица 5.1
n
x
0
x
1
x
2
y
1 + + +
y
1
2 + – +
y
2
3 + + –
y
3
4 + – –
y
4

27
Если реализован план, представленный в табл. 5.1, то векторы-столбцы
210
,, xxx
взаимно ортогональны, т. е.
=
=
),(),(
2010
xxxx
0),(
21
=
=
xx
. Сис-
тема уравнений распадается на независимые уравнения, из которых вычис-
ляются параметры модели:
2,1,0,
),(
),(
),(
===β j
n
yx
xx
yx
j
jj
j
j
Здесь учтено, что скалярные произведения векторов
210
,, xxx
самого
на себя одинаковы и равны количеству измерений.
Корреляционная матрица
β
K для параметров, удовлетворяющих кри-
терию наименьших квадратов, равна матрице, обратной матрице системы ал-
гебраических уравнений для β
r
:
β
K =
1
221202
211101
201000
2
),(),(),(
),(),(),(
),(),(),(
−
−
σ
xxxxxx
xxxxxx
xxxxxx
y
=
=
1
22
11
00
2
),(00
0),(0
00),(
−
−
σ
xx
xx
xx
y
=
=
σ
−
−
−
1
22
1
11
1
00
2
),(00
0),(0
00),(
xx
xx
xx
y
=
=
σ
σ
σ
n
n
n
y
y
y
/00
0/0
00/
2
2
2
.
Параметры некоррелированные и дисперсия их одинакова:
2,1,0,
2
2
=
σ
=σ
β
j
n
y
j
.
Дисперсия выхода линейной модели

28
)1()1(
22
1
22
1
2222
0
ρ+σ=+σ=σ+σ=σ
β
=
β
=
ββ
∑∑
m
j
j
m
j
jy
xx
j
)
,
∑
=
=ρ
m
j
j
x
1
22
.
одинакова на равном расстоянии от центра плана, т. е. ортогональный план
первого порядка является и ротатабельным.
Проверим адекватность модели. Вычисляем остаточную сумму квад-
ратов
I
min
, делим ее на число степеней свободы
1
1
−
−
=
ν
mn
и получаем
остаточную дисперсию (дисперсию адекватности):
∑
=
−
−−
=σ
n
i
ii
yy
mn
1
22
ад
)(
1
1
)
)
.
Здесь y
i
– выход объекта в
i
-й точке эксперимента,
i
y
)
– выход модели
в той же точке. При хорошем описании с помощью модели
y
)
сигнальной
части
)
(
⋅
ϕ
выхода объекта остаточная дисперсия оценивает дисперсию
2
y
σ
выхода объекта.
Плохо, что у остаточной дисперсии
2
ад
σ
)
только одна степень свободы
11241
1
=
−
−
=
−
−
=
ν
mn
. Вынести гарантированное решение с помощью
такой «плохой» оценки нельзя. Для улучшения итогового решения об адек-
ватности модели надо увеличить число степеней свободы оценки
2
ад
σ
)
за счёт
проведения в каждой точке плана нескольких (3–5) измерений. Коррекцию
формул расчёта проведите самостоятельно.
На основе дополнительного эксперимента объема
n
0
в центре плана
строим оценку
2
y
σ
)
для дисперсии
2
y
σ выхода объекта. Число степеней свобо-
ды для оценки
2
y
σ
)
равно величине
ν
2 0
1
=
−
n .
Далее по статистике Фишера
22
ад
/
y
F σσ=
)
)
проверяется гипотеза о ра-
венстве дисперсий. Эта гипотеза совпадает с гипотезой об адекватности мо-
дели. Если статистика
F
не превосходит порогового значения
ανν ,,
2
F
, то
принимается гипотеза об адекватности модели. В противоположном случае
эта гипотеза отвергается. Тогда надо заново строить модель, например, ус-
ложняя ее за счет введения дополнительных факторов, либо отказываться от
линейной модели и переходить к построению квадратичной модели.
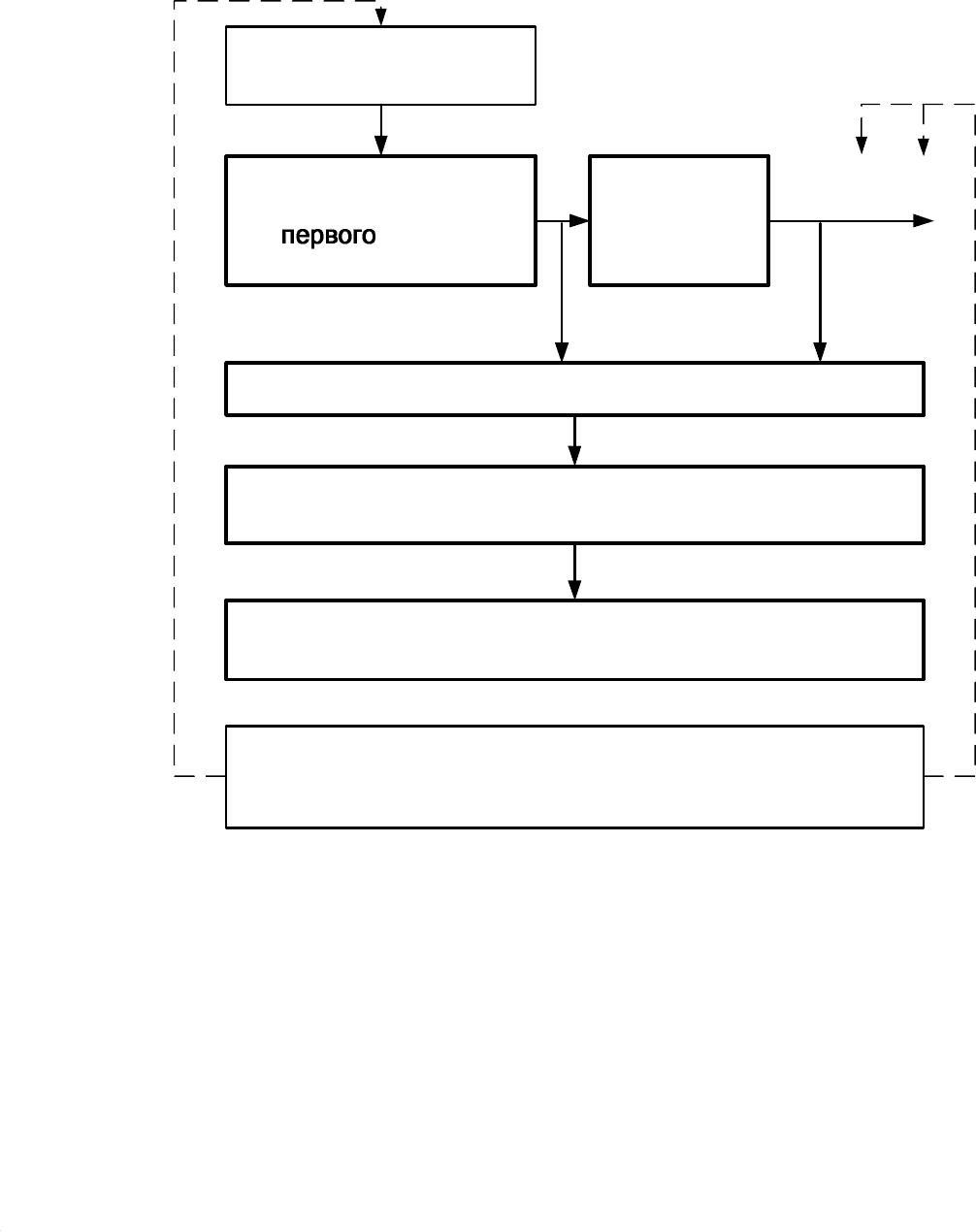
29
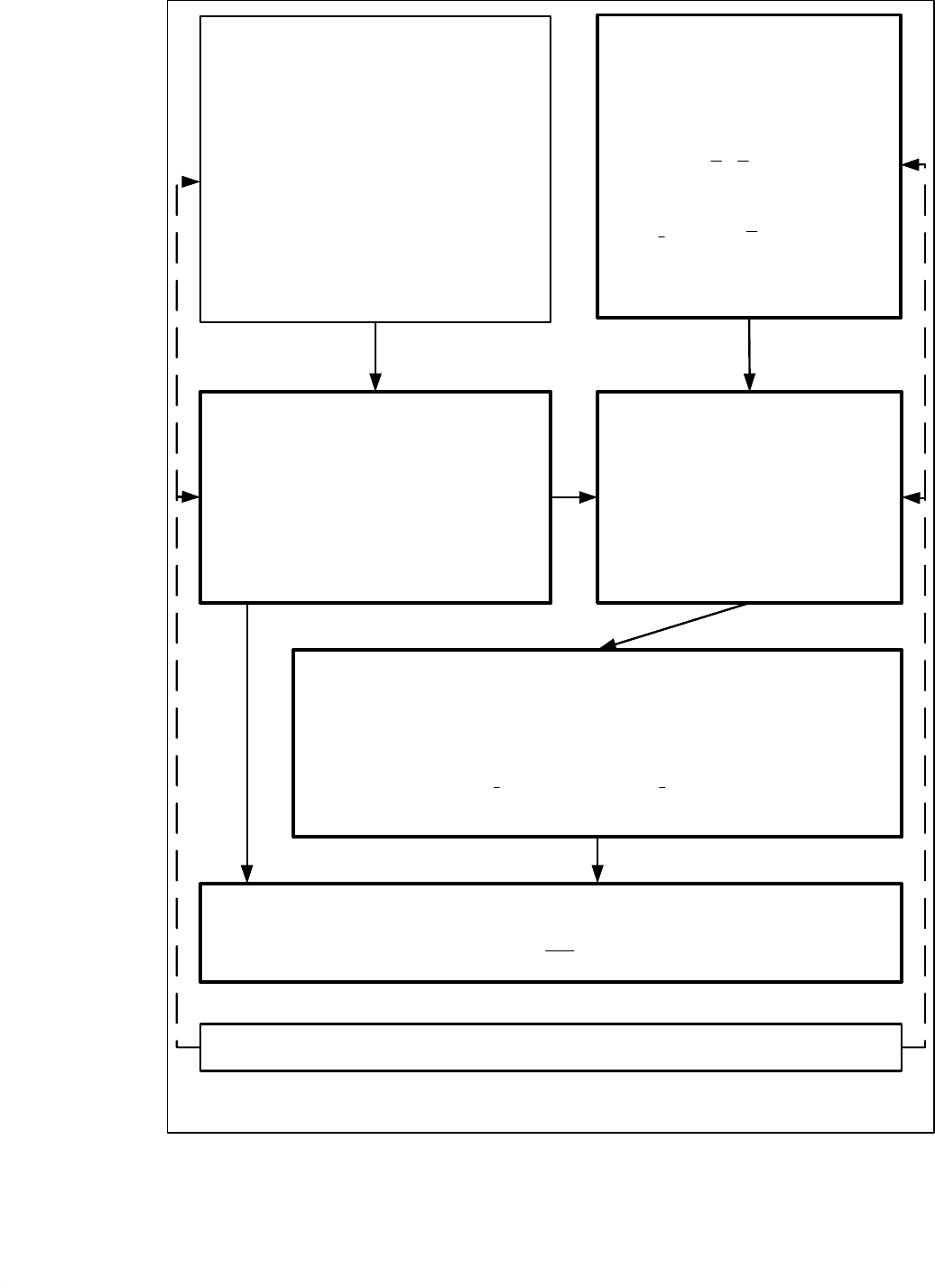
Блок схема последовательности выполнения операций приведена на
рис. 5.3.
Построение квадратичной модели.
При построении более сложной квадратичной модели 2-го порядка
2
2222112
2
11122110
ˆ
xxxxxxy β+β+β+β+β+β≡
Объект
Проверка гипотезы адекватности линейной модели
h
u
y
+
ϕ
=
)
(
Ортогональный план
порядка
База экспериментальных данных входов и выходов
объекта
Исследователь может менять базовую точку, размеры
области поиска, а также сигнальную часть и помеху (при
имитации объекта)
Рисунок 5.3. Блок-схема последовательности выполнения
операций
при построении линейной модели
Базовая точка,
размеры области
поиска
Расчёт параметров линейной степенной модели в
безразмерных и размерных входных переменных
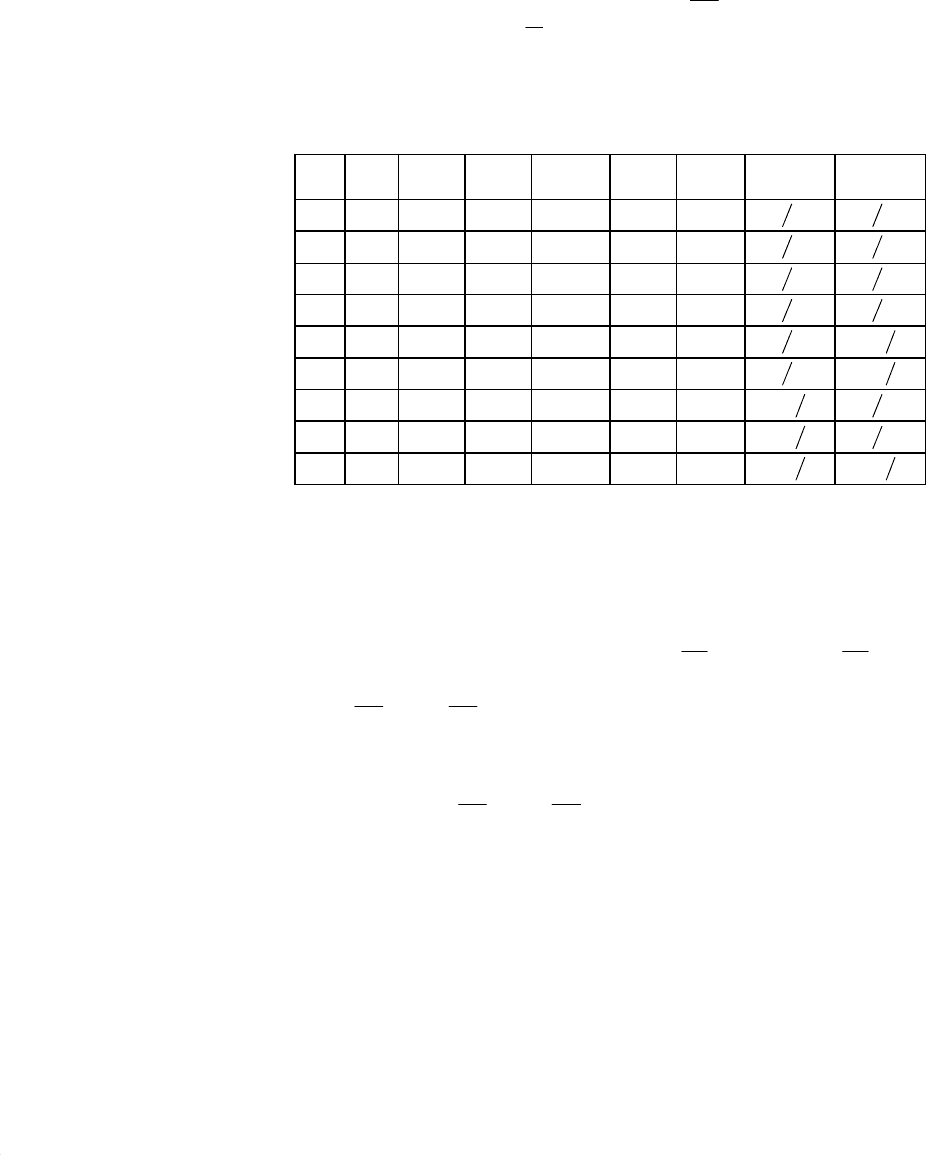
30
Используем композиционный ортогональный (при этом
1
=
α
) план
Бокса – Уилсона – см. таблицу 5.2. Здесь же показана замена столбцов с
квадратичными переменными
x
1
2
,
x
2
2
соответствующими столбцами
1
x
′
,
2
x
′
.
Все элементы каждого столбца
x
1
2
,
x
2
2
отличаются от соответствую-
щих элементов столбцов
1
x
′
,
2
x
′
на свою постоянную величину (среднее
арифметическое):
2,1,
1
1
2222
=−=−=
′
∑
=
ixxx
n
xx
n
i
lllill
Таблица 5.2
n
x
0
1
x
2
x
21
xx
x
1
2
x
2
2
1
x
′
2
x
′
1 + + + + + +
31
31
2 + – + – + +
31
31
3 + + – – + +
31
31
4 + – – + + +
31
31
5 + + 0 0 + 0
31
32
−
6 + – 0 0 + 0
31
32
−
7 + 0 + 0 0 +
32
−
31
8 + 0 – 0 0 +
32
−
31
9 + 0 0 0 0 0
32
−
32
−
В новых переменных все столбцы x
0
,
1
x ,
2
x
,
21
xx
,
1
x
′
,
2
x
′
ортогональ-
ны.
С учетом новых переменных
′
x
l
имеем следующее уравнение модели:
=+
′
β++
′
β+β+β+β+β= )()(
2
2222
2
1111211222110
xxxxxxxxy
)
≡
′
β+
′
β+β+β+β+β+β+β=
22211121122211
2
222
2
1110
xxxxxxxx
222111211222110
xxxxxx
′
β
+
′
β
+
β
+
β
+
β
+
β
′
≡
.
Здесь
2
222
2
11100
xx β+β+β=β
′
.
План реализуется на объекте – см. таблицу 5.3. Например, в точке 5
плана
1
1
=
x
,
0
2
=
x
, что соответствует реальным входным переменным:
