Рубан А.И. Методы анализа данных. Практикум
Подождите немного. Документ загружается.

11
3. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Все необходимые формулы и таблицы с пороговыми значениями для
разных статистик приведены в основном учебном пособии дисциплины.
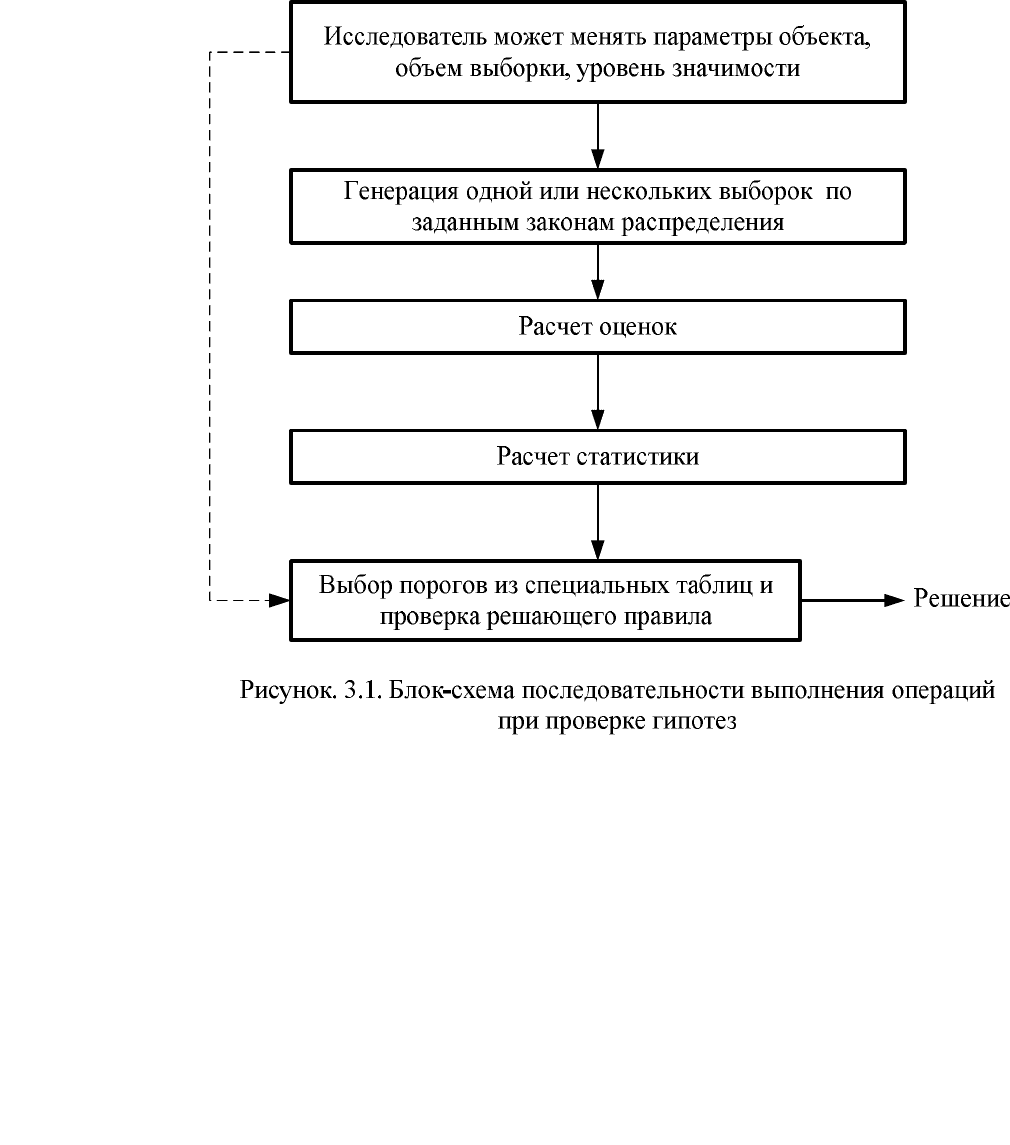
Общая блок-схема для реализации проверок гипотез представлена на
рисунке 3.1.
3.1 Исследование алгоритмов проверки гипотезы о математиче-
ском ожидании
Цель работы: реализация и исследование решающего правила проверки
гипотезы о математическом ожидании.

12
В качестве объекта для исследования следует использовать нормально
распределенную случайную величину
X
.
Входные данные: параметры случайной величины (математическое
ожидание и дисперсия), объем выборки
n
, уровень значимости
α
, известная
величина
m
0
для которой будет производится проверка гипотезы.
Следует рассмотреть оба случая:
• двупороговую процедуру распознавания:
0
: mmH
=
0
: mmH ≠
• однопороговую процедуру распознавания:
0
: mmH
=
Hm m: >
0
Пороговые коэффициенты можно реализовать в виде статического
массива «зашитого» в программу или в виде внешнего файла (что более
предпочтительно).
Для получения оценок математического ожидания и дисперсии объекта
(так как они необходимы для вычисления статистики и дальнейшей ее про-
верки в решающем правиле) необходимо сгенерировать (с использованием
одного из вышеописанных методов генерации нормально распределенных
случайных величин) выборку объема
n
и вычислить оценки по этой выбор-
ки. Рекомендуемый объем выборки
30
≥
n
.
Программный стенд, реализованный в рамках расчетно-графической
работы, должен позволять исследователю (студенту в процессе выполнения
работы и преподавателю в процессе приема работы у студента) вводить все
выше перечисленные входные данные, выполнять одиночные проверки, а так
же реализовывать исследование зависимости решающего правила проверки
гипотезы о математическом ожидании от объема выборки.
3.2 Исследование алгоритмов проверки гипотезы о дисперсиях
Цель работы: реализация и исследование решающего правила проверки
гипотезы о дисперсиях.

13
Необходимо рассмотреть два случая:
1. Гипотезу о равенстве дисперсии некоторой константе.
2. Гипотезу о равенстве дисперсий двух случайных величин.
В первом случае в качестве объекта для исследования следует исполь-
зовать одну нормально распределенную случайную величину
X
.
Во втором случае в качестве объектов для исследования следует ис-
пользовать две случайно распределенных величины
X
и
Y
.
Входные данные: параметры случайных величин (математические
ожидания и дисперсии), объем выборки : для первого случая
n
, для второго
случая
1
n
и
2
n
, уровень значимости
α
, известная величина
2
0
σ
(для первого
случая) для которой будет производится проверка гипотезы.
Для первого случая следует рассмотреть оба варианта:
• двупороговую процедуру распознавания:
2
0
2
: σ=σH
2
0
2
: σ≠σH
• однопороговую процедуру распознавания:
2
0
2
: σ=σH
2
0
2
: σ<σH
Для второго случая рассматривается однопороговая процедура распо-
знавания:
2
2
2
1
: σ=σH
2
1
2
2
: σ<σH
Пороговые коэффициенты можно реализовать в виде статического
массива «зашитого» в программу или в виде внешнего файла (что более
предпочтительно).
Для получения оценок математических ожиданий и дисперсий объек-
тов (так как они необходимы для вычисления статистики и дальнейшей ее
проверки в решающем правиле) необходимо:
Для первого случая сгенерировать одномерную выборку объема
n
и
вычислить оценки по этой выборке. Рекомендуемый объем выборки
30
≥
n
.

14
Для второго случая сгенерировать две одномерных выборки объемом
1
n и
2
n соответственно. Рекомендуемые объемы выборок 30
1
≥
n , 30
2
≥
n .
Программный стенд, реализованный в рамках расчетно-графической
работы, должен позволять исследователю (студенту в процессе выполнения
работы и преподавателю в процессе приема работы у студента) вводить все
выше перечисленные входные данные, выполнять одиночные проверки, а так
же реализовывать исследование зависимости решающего правила проверки
гипотезы о дисперсиях от объема выборки.
3.3 Исследование алгоритмов проверки гипотезы о равенстве ма-
тематических ожиданий
Цель работы: реализация и исследование решающего правила проверки
гипотезы о равенстве математических ожиданий.
В качестве объектов для исследования следует использовать две нор-
мально распределенные случайные величины
X
и
Y
.
Входные данные: параметры случайных величин (математические
ожидания и дисперсии), объемы выборок
1
n
и
2
n
, уровень значимости
α
.
Следует рассмотреть самый общий случай – когда математические
ожидания неизвестны, а дисперсии одинаковы и неизвестны. Тогда задача
решается в два этапа: сначала проверяется гипотеза о равенстве дисперсий
(см. описание предыдущей работы), затем если она выполняется то произво-
дится процедура распознавания:
21
: mmH
=
21
: mmH ≠
Пороговые коэффициенты можно реализовать в виде статического
массива «зашитого» в программу или в виде внешнего файла (что более
предпочтительно).
Для получения оценок математических ожиданий и дисперсий объек-
тов (так как они необходимы для вычисления статистик и дальнейших про-
верок в решающем правиле) необходимо сгенерировать (с использованием
одного из вышеописанных методов генерации нормально распределенных
случайных величин) две одномерных выборки объемом
1
n и
2
n соответст-
венно. Рекомендуемые объемы выборок
30
1
≥
n
,
30
2
≥
n
.

15
Программный стенд, реализованный в рамках расчетно-графической
работы, должен позволять исследователю (студенту в процессе выполнения
работы и преподавателю в процессе приема работы у студента) вводить все
выше перечисленные входные данные, выполнять одиночные проверки, а так
же реализовывать исследование зависимости решающего правила проверки
гипотезы о равенстве математических ожидании от объема выборки и дис-
персий случайных величин
X
и
Y
.
3.4 Исследование алгоритмов проверки гипотезы о выявлении
аномальных измерений
Цель работы: реализация и исследование решающего правила проверки
гипотезы о выявлении аномальных измерений.
В качестве объекта для исследования следует использовать нормально
распределенную случайную величину
X
.
Входные данные: параметры случайной величины (математическое
ожидание и дисперсия), объем выборки
n
, уровень значимости
α
, значение
x
(произвольно вводимое исследователем) для которой будет производится
проверка гипотезы.
Следует рассмотреть двупороговую процедуру распознавания:
X
x
H
∈
:
XxH ∉:
Пороговые коэффициенты можно реализовать в виде статического
массива «зашитого» в программу или в виде внешнего файла (что более
предпочтительно).
Для получения оценок математического ожидания и дисперсии объекта
(так как они необходимы для вычисления статистики и дальнейшей ее про-
верки в решающем правиле) необходимо сгенерировать (с использованием
одного из вышеописанных методов генерации нормально распределенных
случайных величин) выборку объема
n
и вычислить оценки по этой выбор-
ки. Рекомендуемый объем выборки
30
≥
n
.
Программный стенд, реализованный в рамках расчетно-графической
работы, должен позволять исследователю (студенту в процессе выполнения
работы и преподавателю в процессе приема работы у студента) вводить все

16
выше перечисленные входные данные, выполнять одиночные проверки, а так
же реализовывать исследование зависимости решающего правила проверки
гипотезы о выявлении аномальных измерений от объема выборки и диспер-
сии объекта.
3.5 Исследование алгоритма проверки гипотезы об однородности
ряда дисперсий
Цель работы: реализация и исследование решающего правила проверки
гипотезы об однородности ряда дисперсий.
В качестве объектов для исследования следует использовать рад нор-
мально распределенных случайных величин
1
X
,
2
X
,…,
k
X
.
Входные данные: параметры случайных величин (математические
ожидания и дисперсии), объемы всех выборок одинаковые и равны
n
, уро-
вень значимости
α
.
Следует рассмотреть однопороговую процедуру распознавания:
22
2
2
1
:
k
H σ==σ=σ
K
jiH
ji
≠σ≠σ ,:
22
Пороговые коэффициенты можно реализовать в виде статического
массива «зашитого» в программу или в виде внешнего файла (что более
предпочтительно).
Для получения оценок математических ожиданий и дисперсий объек-
тов (так как они необходимы для вычисления статистик и дальнейших про-
верок в решающем правиле) необходимо сгенерировать (с использованием
одного из вышеописанных методов генерации нормально распределенных
случайных величин)
k
одномерных выборок объема
n
. Рекомендуемый объ-
ем выборок
30
≥
n
.
Программный стенд, реализованный в рамках расчетно-графической
работы, должен позволять исследователю (студенту в процессе выполнения
работы и преподавателю в процессе приема работы у студента) вводить все
выше перечисленные входные данные, выполнять одиночные проверки, а так
же реализовывать исследование зависимости решающего правила проверки
гипотезы о равенстве математических ожидании от объема выборки и дис-
персий случайных величин
1
X
,
2
X
,…,
k
X
.

17
3.6 Исследование алгоритма проверки гипотезы о распределениях
Цель работы: реализация и исследование решающего правила проверки
гипотезы о распределениях.
В качестве объекта для исследования следует использовать случайную
величину
X
.
Входные данные: закон распределения и параметры случайной величи-
ны (параметры зависят от закона) и предполагаемый закон распределения,
объем выборки
n
, уровень значимости
α
, число интервалов для построения
гистограммы по выборке.
Выборка генерируется по указанному закону для случайной величины
X
(способ генерации зависит от ее закона).
Затем строится гистограмма и производится проверка гипотзы:
çàêîíîì
âûáðàííûì
ñ
ÿ
ñîãëàñóåòñ
à
ãèñòîãðàìì
:
H
çàêîíîì âûáðàííûì ñ ÿñîãëàñóåòñ íåà ãèñòîãðàìì:H
Программный стенд, реализованный в рамках расчетно-графической
работы, должен позволять исследователю (студенту в процессе выполнения
работы и преподавателю в процессе приема работы у студента) вводить все
выше перечисленные входные данные, выполнять одиночные проверки, а так
же реализовывать исследование зависимости решающего правила проверки
гипотезы о распределении от объема выборки, количества интервалов в гис-
тограмме.

18
4 КЛАССИФИКАЦИЯ В РАСПОЗНАВАНИИ ОБРАЗОВ
4.1 Исследование байесовского правила классификации в распо-
знавании образов при непрерывных информативных признаках (услов-
ные плотности известны с точностью до параметров)
Цель работы: исследование решающего правила классификации при
условиях:
• Имеется два независимых непрерывных информативных призна-
ка
21
, XX и два класса
2
,
1
=
j
;
• Априорные вероятности классов ,2,1),(
=
jjP неизвестны;
• Условные плотности вероятности (при условии истинности того
или иного класса) для информативных признаков известны с
точностью до параметров
2,1),,(
21
=θθ=θ j
jjj
r
r
r
:
2,1),,|(),|(),|,(
221121
=θθ≡θ jjxfjxfjxxf
jjj
r
r
r
;
• известна обучающая выборка объёма
21
nnn
+
=
:
o
11
2
1
1
1
,,,
n
xxx
r
K
r
r
, когда истинным является класс 1;
o
22
2
2
1
2
,,,
n
xxx
r
K
r
r
, когда истинным является класс 2.
За основу берётся байесовское правило классификации с заменой в нём
априорных вероятностей и условных плотностей вероятности их состоятель-
ными оценками:
,2,1),(
ˆ
=jjP
,2,1),
ˆ
,|()
ˆ
,|()
ˆ
,|,(
221121
=θθ≡θ jjxfjxfjxxf
jjj
r
r
r
В результате решающая функция приобретает форму:
)2(
ˆ
)
ˆ
,2|,()1(
ˆ
)
ˆ
,1|,(),(
22112121
PxxfPxxfxx θ−θ=η
r
r
и в пороговом байесовском решающем правиле она сравнивается с нулём:
• если ),(0
21
xx
η
<
, то принимается решение об истинности перво-
го класса;

19
• если же
0),(
21
<
η
xx
, то принимается решение об истинности вто-
рого класса.
По обучающей выборке доопределяются априорные вероятности:
21
21
,)2(,)1( nnn
n
n
P
n
n
P +===
)
)
и параметры
)
ˆ
,
ˆ
(
ˆ
),
ˆ
,
ˆ
(
ˆ
2212221111
θθ≡θθθ≡θ
r
r
r
r
r
r
условных плотностей
)
ˆ
,1|,(
121
θ
r
xxf
,
)
ˆ
,2|,(
221
θ
r
xxf . Причём, первая группа оценок параметров )
ˆ
,
ˆ
(
ˆ
21111
θθ≡θ
r
r
r
находит-
ся по первой части обучающей выборки (когда истинным является класс 1), а
вторая группа оценок параметров )
ˆ
,
ˆ
(
ˆ
22122
θθ≡θ
r
r
r
находится по второй части
обучающей выборки (когда истинным является класс 2).
При исследовании построенного решающего правила (алгоритма рабо-
ты классификатора) за счёт имитации статистических свойств объекта клас-
сификации необходимо получать обучающую выборку. Этот этап обычно
осуществляется следующим образом. Исследователь по своему выбору зада-
ет статистические свойства объекта в виде структуры ),|,(
21 j
jxxf θ
r
и пара-
метров
j
θ
r
условных плотностей вероятности ≡θ ),|,(
21 j
jxxf
r
2,1),,|(),|(
2211
=θθ≡ jjxfjxf
jj
r
r
, априорных вероятностей классов
,2,1),(
=
jjP и общего объема обучающей выборки
n
.
Всё вышеперечисленное объединено в блок-схему последовательности
выполнения операций, представленную на рисунке 4.1.
При составлении плана исследований студенты выделяют варьируемые
переменные (плотности распределения, параметры) на фоне всех возможных
переменных:
1 Структуры условных плотностей вероятности (например, равномер-
ный, нормальный, экспоненциальный др. законы) для объекта классифика-
ции, параметры плотностей, априорные вероятности классов.
2 Структуры выбранных условных плотностей вероятности классифи-
катора, алгоритмы расчёта оценок параметров этих плотностей и априорных
вероятностей классов.
3 Объём обучающей выборки
n
.

20
Затем конкретизируют структуры условных плотностей (это нечисло-
вые, неупорядоченные дискретные переменные) и дискретные числовые зна-
чения соответствующих варьируемых параметров.
Для каждого набора указанных дискретных значений производится вы-
числение оценки вероятности ошибки классификации
n
n
P
îø
îø
ˆ
= , где
ош
n –
число ошибочных решений классификатора на обучающей выборке. В итоге
получается так называемый «куб данных», на основе которого строятся гра-
фики (обычно, двумерные и трёхмерные, хотя могут быть построены и более
полные аналитические степенные квадратичные модели с помощью исполь-
зования планов второго порядка) и дается им объяснение в соответствии с
теорией классификации.
