Richards J.A., Jia X. Remote Sensing Digital Image Analysis: An Introduction

Подождите немного. Документ загружается.

60 2 Error Correction and Registration of Image Data

Fig. 2.18. a Registration

of 1980 image (green)

with 1979 image (red)

using the control points

of Fig. 2.17a, with third

order mapping polynomi-

als; b Third order mapping

of 1980 image (green)

to 1979 image (red) us-

ing the control points of

Fig. 2.17b; c As for b but

using ﬁrst order mapping

polynomials

References for Chapter 2 61

2.6.1

Image Rotation

Rotation of image data by an angle about the pixel grid can be useful for a number

of applications. Most often it is used to align the pixel grid, and thus the image, to

a north- south orientation as treated in Sect. 2.4.2.3. However the transformation in

(2.15) is perfectly general and can be used to rotate any image in an anticlockwise

sense by any speciﬁed angle ζ .

2.6.2

Scale Changing and Zooming

The scales of an image in both the vertical and horizontal directions can be altered

by the transformation.







a 0

0 b





where a and b are the desired scaling factors. To resample the scaled image onto the

display grid we use the inverse operation, as before, to locate pixel positions in the

original image corresponding to each display grid position, viz







1/a 0

01/b





Again interpolation is used to establish actual pixel brightnesses to use, since u, v

will not normally fall on exact grid locations.

Frequently a = b so that the image is simply magniﬁed (although different

magniﬁcation factors could be used in each direction if desired). This is often called

zooming, particularly if the process is implemented in an image display system. If

the nearest neighbour interpolation procedure is used in the resampling process the

zoom implemented is said to occur by pixel replication and the image will look

progressively blocky for larger zoom factors. If cubic convolution interpolation is

used there will be a change in magniﬁcation but the image will not take on the blockly

appearance. Often this process is called interpolative zoom. Both pixel replication

zoom and interpolative zoom can also be implemented in hardware to allow the

process to be performed in real time.

References for Chapter 2

Good discussions on the effect of the atmosphere on image data in the visible and infrared

wavelength ranges will be found in Slater (1980) and Forster (1984). Forster gives a detailed set

of calculations to illustrate how correction procedures for compensating radiometric distortion

caused by the atmosphere are applied. Deﬁnitions and derivations of radiometric quantities

are covered comprehensively by Slater.

Extensive treatments of geometric distortion and means for geometric correction are cov-

ered by Anuta (1973), Billingsley (1983) and Bernstein (1983). Discussions of resampling

62 2 Error Correction and Registration of Image Data

interpolation techniques in particular, and the optimum distribution of control points will be

found in Shlien (1979) and Orti (1981).

An interesting account of geometrical transformations in general, but especially as related

to computer graphics, is found in Foley et al. (1990).

P.E. Anuta, 1973: Geometric Correction of ERTS-1 Digital MSS Data. Information Note

103073, Laboratory for Applications of Remote Sensing, Purdue University, West Lafay-

ette, Indiana.

R. Bernstein, 1983: Image Geometry and Rectiﬁcation. In R.N. Colwell (Ed.) Manual of

Remote Sensing, 2e, Chapter 21, Falls Church, Va. American Society of Photogrammetry.

F.C. Billingsley, 1983: Data Processing and Reprocessing in R.N. Colwell (Ed.) Manual of

Remote Sensing, 2e, Chapter 17, Falls Church, Va. American Society of Photogrammetry.

J.D. Foley, A. Van Dam, S.K. Feiner and J.F. Hughes, 1990: Computer Graphics Principles

and Practice, 2e, Philippines, Addison-Wesley.

B.C. Forster, 1984: Derivation of Atmospheric Correction Procedures for Landsat MSS with

Particular Reference to Urban Data. Int. J. Remote Sensing, 5, 799–817.

J. Yao, 2001: Image Registration Based on Both Feature and Intensity Matching. Proc. IEEE

Conf. on Acoustics, Speech and Signal Processing, 3, 1693–1696.

T.G. Moik, 1980: Digital Processing of Remotely Sensed Images, Washington, NASA.

F. Orti, 1981: Optimal Distribution of Control Points to Minimize Landsat Image Registration

Errors. Photogrammetric Engineering and Remote Sensing, 47, 101–110.

S. Shlien, 1979: Geometric Correction, Registration and Resampling of Landsat Imagery.

Canadian J. Remote Sensing, 5, 74–89.

L.F. Silva, 1978: Radiation and Instrumentation in Remote Sensing. In P.H. Swain & S.M.

Davis (Eds.) Remote Sensing: The Quantitative Approach, N.Y., Mc-Graw-Hill.

K. Simon, 1975: Digital Reconstruction and Resampling for Geometric Manipulation. Proc.

Symp. on Machine Processing of Remotely Sensed Data, Purdue University, June 3–5.

P.N. Slater, 1980: Remote Sensing: Optics and Optical System, Reading, Mass., Addison-

Wesley.

R.E. Turner and M.M. Spencer, 1972: Atmospheric Model for Correction of Spacecraft Data.

Proc. 8th Int. Symp. on Remote Sensing of the Environment, Ann Arbor, Michigan, 895–

934.

M.P. Weinreb, R. Xie, I.H. Lienesch and D.S. Crosby, 1989: Destriping GOES Images by

Matching Empirical Distribution Functions. Remote Sensing of Environment, 29, 185–

195.

Problems

2.1 (a) Consider a (hypothetical) region on the ground consisting of a square grid. For sim-

plicity suppose the grid “lines" are 79 m in width and the grid spacing is 790 m. Sketch

how the region would appear in Landsat multispectral scanner imagery, before any geometric

correction has been applied. Include only the effect of earth rotation and the effect of 56 m

horizontal spacing of the 79 m × 79 m ground resolution elements.

(b) Develop a pair of linear (ﬁrst order) mapping polynomials that will correct the image

data of part (a). Assume the “lines" on the ground have a brightness of 100 and the background

brightness is 20. Resample onto a 50 m grid and use a nearest neighbour interpolation.You will

not want to compute all the resampled pixels unless a small computer program is used for the

Problems 63

purpose. Instead you may wish simply to consider some signiﬁcant pixels in the resampling

to illustrate the accuracy of the geometric correction.

2.2 A sample of pixels from each of three cover types present in the Landsat MSS scene of

Sydney, Australia, acquired on 14 December, 1980 is given in Table 2.2a. Only the brightnesses

(digital count values) in the visible red band (0.6 to 0.7 µm) and the second of the infrared

bands (0.8 to 1.11 µm) are given.

For this image Forster (1984) has computed the following relations between reﬂectance

(R) and the digital count values (C) measured in the image data, where the subscript 7 refers

to the infrared data and the subscript 5 refers to the visible red data:

=0.44 C

+ 0.5

=1.18 C

+ 0.9 .

Table 2.2b shows sampIes of MSS digital count values for Sydney acquired on 8 June

1980. For this scene, Forster has determined

Table 2.2. Pixels from three cover types in wavelength bands 5 (0.6 to 0.7 µm) and 7 (0.8 to

1.1 µm) (on a scale of 0 to 255)

(a) Landsat MSS image of Sydney, 14 December 1980

64 2 Error Correction and Registration of Image Data

=3.64 C

− 1.6

=1.52 C

− 2.6 .

Compute mean values of the digital count values for each cover type in each scene and

plot these (along with bars that indicate standard deviation) in a multispectral space. This has

two axes; one is the pixel digital value in the infrared band and the other is the value in the

visible red band.

Instead of plotting the mean and standard deviations of the digital count values, convert

the data to reﬂectances ﬁrst. Comment on the effect correction of the raw digital count values

to reﬂectance data (in which atmospheric effects have been removed) has on the apparent

spectral separation of the three cover types.

2.3 Aircraft line scanners acquire image data using a mirror that sweeps out lines of data at

right angles to the fuselage axis. In the absence of a cross wind, scanning therefore will be

orthogonal to the aircraft ground track, as is the case for satellite scanning. However aircraft

data is frequently recorded in the presence of a cross wind. The aircraft fuselage then maintains

an angle to the ground track so that scanning is no longer orthogonal to the effective forward

motion. Discuss the nature of the distortion, referred to as “crabbing", that this causes in the

image data as displayed on a rectangular grid. Remember to take account also of the ﬁnite

scan time across a line.

Push broom scanners, employing linear arrays of charge coupled device sensors, are also

used on aircraft. What is the nature of the geometric distortion incurred with those devices in

the presence of a crosswind?

It is technically feasible to construct two dimensional detector arrays for use as aircraft

sensors, with which frames of images data would be recorded in a “snapshot fashion" much

like the Landsat RBV. What geometric distortion would be incurred with this device as a result

of a cross-wind?

2.4 Compute the skew distortion resulting from earth rotation in the case of Landsats 7, and

Spot.

2.5 For a particular application suppose it was necessary to apply geometric correction pro-

cedures to an image prior to classiﬁcation. (See Chap. 3 for an overview of classiﬁcation).

What interpolation technique would you see use in the resampling process? Why?

2.6 Destriping of Landsat multispectral scanner images is often performed by computing six

(modulo-6 line) histograms and then either (i) matching all six to a standard histogram or

(ii) choosing one of the six as a reference and matching the other ﬁve to it. Which method is

to be preferred if the image is to be analysed by photointerpretation or by classiﬁcation (see

Chap. 3)?

2.7 In a particular problem you have to register ﬁve Landsat images to a map. Would you

four images to that one, or image 1 to the map, image 2 to image 1, image 3 to image 2 etc?

2.8 (Requires a background in digital signal processing and sampling theory).

Remote sensing digital images are simply two dimensional uniform samples of the ground

scene. In particular one line of image data is a regular sequence of samples. The spatial

frequency spectrum of the line data will therefore be periodic as depicted in Fig. 2.19; it is

assumed here there is no aliasing. From sampling theory it is well known that the original

data can be recovered by low pass ﬁltering the spectrum, using the ideal ﬁlter as indicated in

the ﬁgure. Multiplication of the spectrum by this ideal ﬁlter is equivalent to convolving the

Problems 65

Fig. 2.19. Spatial frequency spectrum of the line data

original line samples by the inverse Fourier transform of the ﬁlter function. From the theory

of the Fourier transform, the inverse of the ﬁlter function is

s(x) =

sin x

with x = ζ/2d in which ζ is a spatial variable along lines of data, and d is the inter-pixel

spacing. This is known generally as an interpolating function. Determine some cubic polyno-

mial approximations to this function. These could be determined from a simple Taylor series

expansion or could be derived from cubic splines. For a set of examples see Shlien (1979).

2.9 A multispectral scanner has been designed for aircraft operation. It has a ﬁeld of view

(FOV) of ±35

◦

about nadir and an instantanteous ﬁeld of view (IFOV) of 2 mrad. The sensor

is designed to operate at a ﬂying height of 1000 m.

(i) Determine the pixel size, in metres, at nadir.

(ii) Determine the pixel size at the edge of a swath compared with that at nadir.

(iii) Discuss the nature of the distortion in the image geometry encountered if the pixels across

a scan line are displayed on uniform pixel centre.

2.10 Determine the maximum angle of the ﬁeld of view for an airborne optical sensor with a

constant instantaneous ﬁeld of view (IFOV), so that the pixel dimension along the scan line

at the extremes is less than 1.5 times that at nadir (ignore earth curvature effect).

2.11 Consider the panoramic along scan line distortion of an airborne optical remote sensing

system with a constant instantaneous ﬁeld of view (IFOV); sketch the image formed for the

ground scene shown in Fig. 2.20, and explain why it appears as you have sketched it.

Fig. 2.20. Ground scene

The Interpretation of Digital Image Data

3.1

Approaches to Interpretation

When image data is available in digital form, spatially quantised into pixels and

radiometrically quantised into discrete brightness levels, several approaches are pos-

sible in endeavouring to extract information. One involves the use of a computer

to examine each pixel in the image individually with a view to making judgement

about pixels speciﬁcally based upon their attributes. This is referred to as quantita-

tive analysis since pixels with like attributes are often counted to give area estimates.

Means for doing this are described in Sect. 3.4. Another approach involves a human

analyst/interpreter extracting information by visual inspection of an image composed

from the image data. In this he or she notes generally large scale features and is often

unaware of the spatial and radiometric digitisations of the data,. This is referred to

as photointerpretation or sometimes image interpretation; its success depends upon

the analyst exploiting effectively the spatial, spectral and temporal elements present

in the composed image product. Information spatially, for example, is present in the

qualities of shape, size, orientation and texture. Roads, coastlines and river systems,

fracture patterns, and lineaments generally, are usually readily identiﬁed by their

spatial disposition. Temporal data, such as the change in a particular object or cover

type in an image from one date to another can often be used by the photointerpreter

as, for example, in discriminating deciduous or ephemeral vegetation from perennial

types. Spectral clues are utilised in photointerpretation based upon the analyst’s fore-

knowledge of, and experience with, the spectral reﬂectance characteristics of typical

ground cover types, and how those characteristics are sampled by the sensor on the

satellite or aircraft used to acquire the image data.

Those two approaches to image interpretation have their own roles and often

these are complementary. Photointerpretation is aided substantially if a degree of

digital image processing is applied to the image data beforehand, while quantitative

analysis depends for its success on information provided at key stages by an analyst.

This information very often is drawn from photointerpretation.

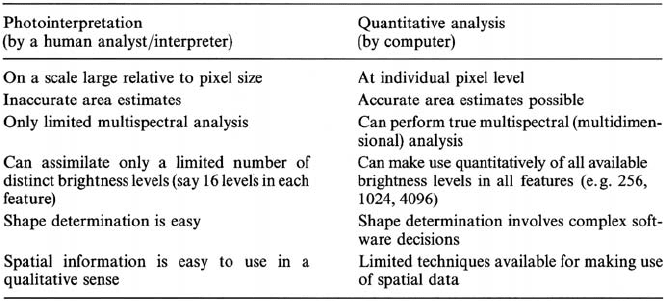
68 3 The Interpretation of Digital Image Data

Table 3.1. A comparison of photointerpretation and quantitative analysis

A comparison of the attributes of photointerpretation and quantitative analysis

is given in Table 3.1. From this it can be concluded that photointerpretation, involv-

ing direct human interaction and therefore high level decisions, is good for spatial

assessment but poor in quantitative accuracy. Area estimates by photointerpretation,

for instance, would involve planimetric measurement of regions identiﬁed visually;

in this, boundary deﬁnition errors will prejudice area accuracy. By contrast, quan-

titative analysis, requiring little human interaction, has poor spatial ability but high

quantitative accuracy. Its high accuracy comes from the ability of a computer, if re-

quired, to process every pixel in a given image and to take account of the full range

of spectral, spatial and radiometric detail present. Its poor spatial properties come

from the relative difﬁculty with which decisions about shape, size, orientation and

texture can be made using standard sequential computing techniques.

In computer-based quantitative analysis the attributes of each pixel (such as the

spectral bands available) are examined in order to give the pixel a label identifying

it as belonging to a particular class of pixels of interest to the user. As a result, the

process is often also called classiﬁcation. We will consider that process in a little

more detail shortly. In the particular case of hyperspectral data, because of the high

spectral deﬁnition available, pixel identiﬁcation and thus classiﬁcation is possible

using knowledge of the spectroscopic properties of earth surface materials. It is also

a quantitative approach because identiﬁcation happens at the pixel level. Although

the knowledge of an expert analyst is used in performing the identiﬁcation, most

often the spectrum of a pixel recorded by a hyperspectral sensor is identiﬁed by

comparing it against a data base of pre-recorded spectra (see Chap. 13).

3.2 Forms of Imagery for Photointerpretation 69

3.2

Forms of Imagery for Photointerpretation

Image data can be procured either in photographic form or in digital format. The

latter is more ﬂexible since ﬁrst, photographic products can be created from the

digital data and secondly, the data can be processed digitally for enhancement before

visual interpretation.

There are two fundamental types of display product. The ﬁrst is a black and white

display of each band in the image data. If produced from the raw digital data then

black will correspond to a digital brightness value of 0 whereas white will correspond

to the highest digital value. This is usually 63, 127, 255 or 4095 (for 6 bit, 7 bit, 8 bit

and 12 bit data respectively).

The second display product is a colour composite in which selected features

or bands in multispectral data are chosen to be associated with the three additive

colour primaries in the display device which produces the colour product. When

the data consists of more than three features a judgement has to be made as to

how to discard all but three, or alternatively, a mapping has to be invented that will

allow all the features to be combined suitably into the three primaries. One possible

mapping is the principal components transformation developed in Chap. 6. Usually

this approach is not adopted since the three new features are synthetic and the analyst

is therefore not able to call upon experience of spectral reﬂectance characteristics.

Instead a subset of original bands is chosen to form the colour composite. When

the data available consists of a large number of bands (such as produced by aircraft

scanners or by imaging spectrometers) only experience, and the area of application,

tell which three bands should be combined into a colour product. For data with

limited spectral bands however the choice is more straightforward. An example of

this is Landsat multispectral scanner data. Of the available four bands, frequently

band 6 is simply discarded since it is highly correlated with band 7 for most cover

types and also is more highly correlated with bands 4 and 5 than is band 7. Bands 4,

5 and 7 are then associated with the colour primaries in the order of increasing

wavelength:

Landsat MSS Bands

4 (green)

5 (red)

7 (infrared)

→

increasing

wavelenth

Colour primaries

blue

green

red

An example of the colour product obtained by such a procedure is seen in Fig. 3.1.

This is often referred to as a false colour composite or sometimes in the past, by

association with colour infrared ﬁlm, a colour infrared image. In this, vegetation

shows as variations in red (owing to the high infrared response associated with

vegetation), soils show as blue, green and sometimes yellow and water as black

70 3 The Interpretation of Digital Image Data

Fig. 3.1. Formation of a Landsat multispectral scanner false colour composite by displaying

the infrared band as red, the visible red band as green and the visible green band as blue

or deep blue. These colour associations are easily determined by reference to the

spectral reﬂectance characteristics of earth surface cover types in Sect. 1.1; it is

important also to take notice of the spectral imbalance created by computer en-

hancement of the brightness range in each wavelength band as discussed in Sect. 3.3

following.