Richards J.A., Jia X. Remote Sensing Digital Image Analysis: An Introduction

Подождите немного. Документ загружается.

274 10 Feature Reduction

As with divergence, an average pairwise JM distance can be deﬁned according to

ave



i=1



j=i+1

p(ω

)p(ω

(10.7)

where M is the number of spectral classes and p(ω

), p(ω

) are the class prior

probabilities.

10.2.3.2

Comparison of Divergence and JM Distance

JM distance performs better as a feature selection criterion for multivariate normal

classes than divergence for the reasons given above; however it is computationally

more complex and thus expensive to use as can be assessed from comparison of (10.2)

and (10.6). Suppose a particular problem involves M spectral classes. Consider the

cost then of computing all pairwise divergences and all pairwise JM distances. These

costs can be assessed largely on the basis of having to compute matrix inverses and

determinants, assuming reasonably that they involve similar computational demands

using numerical procedures. In the case of divergence it is necessary to compute only

M matrix inverses to allow all the pairwise divergences to be found. However for

JM distance it is necessary to compute

+ M equivalent matrix inverses since

the individual class covariances appear as pairs which have to be added and then

inverted. It may be noted that

+ M =

M(M + 1) so that divergence is a

factor of

(M + 1) more economical to use. When it is recalled how many feature

subsets may need to be checked in a feature selection exercise this is clearly an

important consideration. However the unbound nature of divergence as discussed in

Sect. 10.2.2.4 throws doubt on its usefulness.

10.2.4

Transformed Divergence

10.2.4.1

Deﬁnition

A useful modiﬁcation of divergence becomes apparent by noting the algebraic sim-

ilarity of divergence to the parameter B in JM distance, as deﬁned in (10.6). Since

both involve terms which are functions of the covariance alone, and terms which

appear as normalised distances between class means, it should be possible to make

use of a heuristic transformed divergence measure of the form (Swain and Davis

1978)

= 2(1 − e

−d

). (10.8)

Because of its exponential character it will have a saturating behaviour with in-

creasing class separation, as does JM distance, and yet it is computationally more

10.2 Separability Measures for Multivariate Normal Spectral Class Models 275

economical. This saturating measure is used in the software package called Multi-

Spec; it has been demonstrated to be almost as effective as JM distance in feature

selection, and considerably better than simple divergence or simple Bhattacharyya

distance (Swain et al., 1971, Mausel et al., 1990).

10.2.4.2

Relation Between Transformed Divergence

and Probability of Correct Classiﬁcation

It can be shown that the probability of making a classiﬁcation error in placing a

pattern into one of two (equal prior probability) classes with a pairwise divergence

is bound by (Kailath, 1967)

−d

so that the probability of correct classiﬁcation is bound by

< 1 −

−d

Since d

=−8ln



1 −



from (10.8),

then P

< 1 −



1 −



. (10.9)

This bound on classiﬁcation accuracy is shown in Fig. 10.5 along with an empirical

relationship between transformed divergence and probability of correct (pairwise)

classiﬁcation derived by Swain and King (1973). This ﬁgure has considerable value

in establishing a priori the upper bound achievable on classiﬁcation accuracy for an

existing set of spectral classes.

Fig. 10.5. Probability of correct classiﬁcation as

a function of pairwise transformed divergence.

The empirical measure, taken from Swain and

King (1973), was determined using 2790 sets of

multidimensional, normally distributed data, in

two classes

276 10 Feature Reduction

10.2.4.3

Use of Transformed Divergence in Clustering

One of the last stages in a practical clustering algorithm is to evaluate the size and

relative locations of the clusters produced, as noted in Chap. 9. If clusters are too close

to each other they should be merged. The availability of the information in Fig. 10.5

allows merging to be effected based upon a pre-speciﬁed transformed divergence,

since both cluster mean and covariance data is normally available. By establishing

a desired accuracy level (in fact upper bound) for the subsequent classiﬁcation and

then determining the corresponding value of transformed divergence, clusters with

separabilities less than this value must be merged.

10.3

Separability Measures for Minimum Distance Classiﬁcation

The separability measures of Sect. 10.2 relate to spectral classes modelled by mul-

tivariate normal distributions, in preparation for maximum likelihood classiﬁcation.

Should another classiﬁer be used this procedure is unduly complex and largely with-

out meaning. For example, if supervised classiﬁcation is to be carried out using

the minimum distance to class means technique there is no advantage in using

distribution-based separability measures, since probability distribution class mod-

els are not employed. Instead it is better to use a simple measure consistent with the

nature of the classiﬁcation algorithm. For minimum distance calculation this would

be a distance measure, computed according to the particular distance metric in use.

Commonly this is Euclidean distance. Consequently, when a set of spectral classes

has been determined, ready for the classiﬁcation step, the complete set of pairwise

Euclidean distances will provide an indication of class similarities. Unfortunately this

cannot be related to an error probability (for misclassiﬁcation) but ﬁnds application

as an indicator of what pairs of classes could be merged, if so desired.

10.4

Feature Reduction by Data Transformation

The emphasis of the preceding sections has been feature selection – i.e., an evaluation

of the existing set of features for the pixel data in multispectral imagery with a view

to selecting the most discriminating, and discarding the rest. It is also possible to

effect feature reduction by transforming the data to a new set of axes in which

separability is higher in a subset of the transformed features than in any subset of

the original data. This allows transformed features to be discarded. A number of

image transformations could be entertained for this; however the most commonly

encountered in remote sensing are the principal components or Karhunen-Loève

transform and the transformation associated with so-called canonical analysis. These

are treated in the following.

10.4 Feature Reduction by Data Transformation 277

10.4.1

Feature Reduction Using the Principal Components Transformation

The principal components transformation (see Chap. 6) maps image data into a new,

uncorrelated co-ordinated system or vector space. Moreover, in doing so, it produces

a space in which the data has most variance along its ﬁrst axis, the next largest

variance along a second mutually orthogonal axis, and so on. The later principal

components would be expected, in general, to show little variance. These could be

considered therefore to contribute little to separability and could be ignored, thereby

reducing the essential dimensionality of the classiﬁcation space and thus improving

classiﬁcation speed. This is only of value however if the spectral class structure of

the data is distributed substantially along the ﬁrst few axes. Should this not be the

case it is possible that feature reduction of the transformed data may be no more

likely than with the original data. In such a case the technique of canonical analysis

may be a better approach.

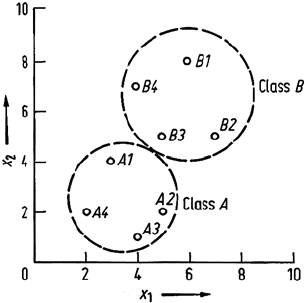
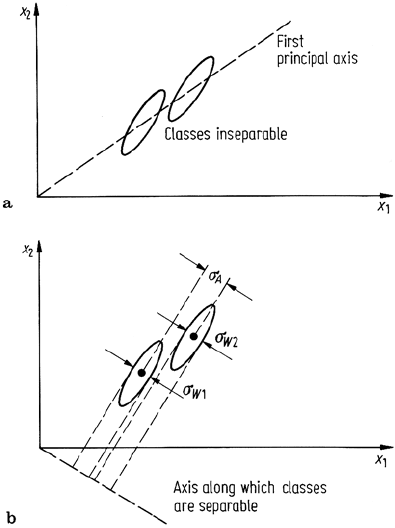
As an illustration of a situation of data in which principal components transfor-

mation does allow feature reduction, consider the two class two dimensional data

illustrated in Fig. 10.6. Assume that the classes are not separable in either of the

original data variables alone but rather both dimensions are required for separability.

However, inspection indicates that the ﬁrst component of a principal components

transform will yield class separability. This is now demonstrated mathematically by

presenting the results of hand calculations on the data.

Notwithstanding the class structure of the data the principal components trans-

formation makes use of a global mean and global covariance. Using (6.1) and (6.2)

it is shown readily that

m =



4.5

4.25



and

Σ =



2.57 1.86

1.86 6.21



Fig. 10.6. Two dimensional, two class data in

which feature reduction using principal com-

ponents analysis is possible

278 10 Feature Reduction

The eigenvalues of the covariance matrix are λ

= 6.99 and λ

= 1.79 so that

the ﬁrst principal component will contain 79.6% of the variance. The normalised

eigenvectors corresponding to these eigenvalues are



0.387

0.922



and g



−0.922

0.387



so that the principal components transformation matrix is

G =



0.387 0.922

−0.922 0.387



= D

in (6.4).

Using this matrix, the ﬁrst principal component of each pixel vector can be computed

according to

= 0.387x

+ 0.922x

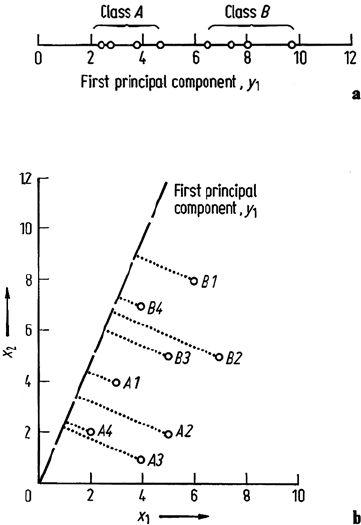
These are shown plotted in Fig. 10.7a in which it is seen that the ﬁrst principal

component is sufﬁcient for separation. Figure 10.7b shows the principal axes relative

to the original image components.

Fig. 10.7. a First principal component

of the image data; b principal axis rel-

ative to original image components

10.4 Feature Reduction by Data Transformation 279

10.4.2

Canonical Analysis as a Feature Selection Procedure

The principal components transformation is based upon the global covariance matrix

of the full set of image data and thus is not sensitive explicitly to class structure in

the data. The reason it often works well in remote sensing as a feature reduction

tool is a result of the fact that classes are frequently distributed in the direction

of maximum data scatter. This is particularly so for soils and spectrally similar

cover types. Should good separation not be afforded by the principal components

transformation derived from the global covariance matrix then a subset of image data

could be selected that embodies the cover types of interest and this subset used to

compute a covariance matrix. The resulting transformation will have its ﬁrst principal

axes oriented so that the cover types of interest are well discriminated. Another, more

rigorous, method for generating a transformed set of feature axes, in which class

separation is optimised, is based upon the procedure called canonical analysis. To

illustrate this approach consider the contrived two dimensional, two class data shown

in Fig. 10.8. By inspection, the classes can be seen not to be separable in either of the

original feature axes on their own. Nor will they be separable in only one of the two

principal component axes because of the nature of the global data scatter compared

with the scatter of data within the individual classes.

Fig. 10.8. a Hypothetical two

dimensional, two class data il-

lustrating lack of separability in

either original band or in either

principal component; b axis along

which classes can be separated

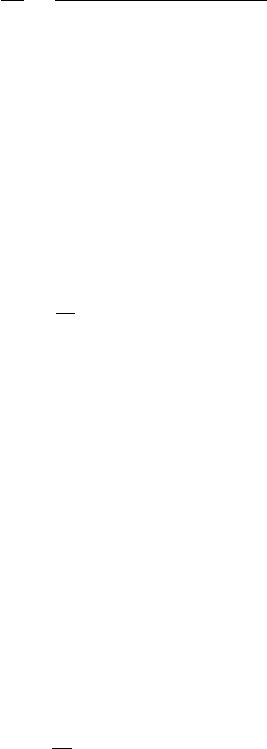
280 10 Feature Reduction

Inspection shows however that the data of Fig. 10.8a can be separated by a sin-

gle feature if an axis rotation (i.e. an image transformation) such as that shown in

Fig. 10.8b is adopted. A little thought reveals that the primary axis in this new trans-

formation should be so-oriented that the classes have the largest possible separation

between their means when projected onto that axis, while at the same time they

should appear as small as possible in their individual spreads. If we characterise the

former by a measure σ

as illustrated in the diagram (which can be referred to as the

standard deviation among the classes – it is as if the classes themselves were data

points at their mean positions) and the spread of data within classes as seen on the

new axis as σ

,σ

as illustrated (these are the standard deviations of the classes)

then our interest is in ﬁnding a new axis for which

among categories variance

within categories variance

(10.10)

is as large as possible. Here σ

is the average of σ

and σ

for the example of

Fig. 10.8.

10.4.2.1

Within Class and Among Class Covariance Matrices

To handle data with any number of dimensions it is necessary to deﬁne average

data scatter within the classes, and the scatter of the classes themselves around the

multispectral space, by covariance matrices.

The average within class covariance matrix is deﬁned as



i=1

(10.11a)

where Σ

is the covariance matrix of the data in class i and where M is the total

number of classes. The boldface sigma is printed for the summation to distinguish it

from the symbol for covariance. Equation (10.11a) applies only if the classes have

equal populations. A better expression is

⎧

⎨

⎩



i=1

− 1)Σ

⎫

⎬

⎭

(10.11b)

where n

is the population of the ith class and S



i=1

The among class covariance matrix is given by

= E{(m

− m

)(m

− m

)

} (10.12)

where m

is the mean of the ith class, E is the expectation operator and m

is the

global mean, given by



i=1

(10.13a)

10.4 Feature Reduction by Data Transformation 281

where the classes have equal populations, or



i=1

(10.13b)

in general.

10.4.2.2

A Separability Measure

Let y = D

x be the required transformation that generates the new axes y in which

the classes have optimal separation. The transposed form of the transformation matrix

is chosen here to simplify the following expressions. By the same procedure that was

used for the principal components transformation in Sect. 6.1.2 it is possible to show

that the within class and among class covariance matrices in the new co-ordinate

system are

w,y

= D

w,x

D (10.14a)

A,y

= D

A,x

D (10.14b)

where the subscripts x and y have been used to identify the matrices with their re-

spective co-ordinates. It is signiﬁcant to realise here, unlike with the case of principal

components analysis, that the two new covariance matrices are not necessarily diag-

onal. However, as with principal components the row vectors of D

deﬁne the axis

directions in y-space. Let d

be one particular vector (say the one that deﬁnes the

ﬁrst so-called canonical axis, along which the classes will be optimally separated),

then the corresponding within class and among class variances will be

= d

w,x

= d

A,x

d .

What we wish to do is to ﬁnd the d, (and in fact ultimately the full transformation

matrix D

) for which

λ = σ

/σ

= d

A,x

d/d

w,x

d (10.15)

is maximised. In the following the axis subscripts on the covariance matrices have

been dropped for convenience.

10.4.2.3

The Generalised Eigenvalue Equation

The ratio of variances λ in (10.15) is maximised by the selection of d if

∂λ

∂d

= 0.

282 10 Feature Reduction

Noting the identity that

∂

∂x

Ax}=2Ax then

∂λ

∂d

∂

∂d

{(d

d)(d

−1

}

= 2Σ

d(d

−1

− 2Σ

d(d

d)(d

−2

= 0.

This reduces to

d − Σ

d(d

d)(d

−1

= 0.

Which can be written as

(Σ

− λΣ

)d = 0 (10.16)

Equation (10.16) is called a generalised eigenvalue equation and has to be solved

now for the unknowns λ and d. The ﬁrst canonical axis will be in the direction of

d and λ will give the associated ratio of among class to within class variance along

that axis.

In general (10.16) can be written

(Σ

− Σ

)D = 0 (10.17)

where  is a diagonal matrix of the full set of λ’s and D is the matrix of vectors d.

The development to this stage is usually referred to as discriminant analysis. One

additional step is included in the case of canonical analysis.

As with the equivalent step in the principal components transformation, solu-

tion of (10.16) amounts to ﬁnding the set of eigenvalues λ and the corresponding

eigenvectors, d. While unique values for λ can be determined the components of

d can only be found relative to each other. In the case of principal components we

introduced the additional requirement that the vectors have unit magnitude, thereby

allowing the vectors to be determined uniquely. For canonical analysis, the additional

constraint used is

D = I. (10.18)

This says that the within class covariance matrix after transformation must be the

identity matrix (i.e. a unit diagonal matrix). In other words, after transformation, the

classes should appear spherical.

For M classes and N bands of multispectral data, if N>M− 1 there will

only be M − 1 non-zero roots of (10.17) and thus M − 1 canonical axes (Seal,

1964). For this example, in which N = 2,M = 2, one of the eigenvalues of (10.16)

will be zero and thus the corresponding eigenvector will not exist. This implies that

the dimensionality of the transformed space will be less than that of the original

data. Thus canonical analysis provides separability with reduced dimensionality. In

general, in the ﬁrst canonical axis, corresponding to the largest λ, the classes will

have maximum separation. The second axis, corresponding to the next largest λ, will

provide the next best degree of separation, and so on. Campbell and Atchley (1981)

review canonical analysis with a particular emphasis on a geometrical interpretation.

10.4 Feature Reduction by Data Transformation 283

10.4.2.4

An Example

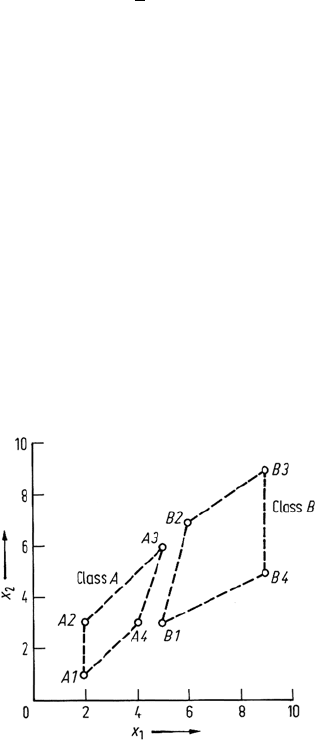
Consider the two dimensional, two category data shown in Fig. 10.9. Both of the

original features x

and x

are required to discriminate between the categories. We

will now perform a canonical analysis transformation on the data to show that the

categories can be discriminated in the ﬁrst canonical axis.

The individual covariance matrices of the classes are



2.25 2.59

2.59 4.25





4.25 3.00

3.00 6.67



so that the within class covariance is

{Σ

+ Σ



3.25 2.80

2.80 5.46



The among class covariance matrix is



8.00 5.50

5.50 3.78



The canonical transformation matrix D

is given by a solution to (10.17) where D

is a matrix of column vectors. These vectors are the axes in the transformed space,

along the ﬁrst of which the ratio of among categories variance to within categories

variance is greatest.Along this axis there is most chance of separating the classes.  is

a diagonal matrix of scalar constants that are the eigenvalues of (10.17); numerically

these are the ratios of variances along each of the canonical axes.

Each λ and the accompanying d can be found readily by considering the individ-

ual component equation (10.16) rather than the more general form in (10.17). For

(10.16) to have a non-trivial solution it is necessary that the determinant

|Σ

− λΣ

|=0.

Fig. 10.9. Two classes of two dimensional

data, each containing 4 data points