Ramanathan Sh. (Ed.) Thin Film Metal-Oxides: Fundamentals and Applications in Electronics and Energy

Подождите немного. Документ загружается.

220 U.V. Waghmare

6.2.5.2 Interfaces and Superlattices

To explore the realistic lower limit on the thickness of a ferroelectric slab below

which ferroelectricity may be suppressed, Junquera and Ghosez [46] carried out

ﬁrst-principles investigation of the stability of uniformly polar off-centering of ions

in BaTiO

ﬁlms of thickness 2–4 nm, sandwiched between SrRuO

electrodes. They

demonstrated that a polar state is favorable energetically only for thicknesses above

six unit cells (2.4 nm) of BaTiO

. These results could be understood within a simple

electrostatic model where screening of the depolarization ﬁeld inside the ﬁlm by

carriers in the electrodes is partial. This work, however, did not assess the relative

stability of the uniformly polarized state and the one with polar domains.

First-principles estimation of height of electronic energy barriers at metal–

insulator interfaces has been limited because band-gaps are underestimated in DFT

calculations. The locations of metal induced gap states and Fermi energy in the gap

are not reliably predicted from such calculations. For insulator–insulator interfaces,

only the valence band off-sets can be estimated reliably from such calculations and

used along with knowledge of the experimental band gaps to estimate conduction

band offsets. Reader is referred to the review article [1] for pointers to such ﬁrst-

principles studies in the context of ferroelectrics.

We point out that most studies of interfaces of ABO

perovskites with metals

and insulating oxides have been carried out with perfect lattice matching, and not

allowing for cell multiplying (change in periodicity) in the plane of the interface.

This excludes the possibility of formation of domains (particularly at longer length-

scales), which is very likely to occur when there is partial compensation of the

depolarization ﬁeld. For example, when the dielectric layer is reasonably thick, or

the electrode material is not a good metal, formation of domain structures is very

much likely. This will be taken up in discussions based on analysis of the effec-

tive Hamiltonian (which is necessary to access long length-scales associated with

domains).

Superlattices based on thin .1 nm/ layers of two (or more) different ABO

ox-

ides are very interesting because (a) of their richness of fundamental mechanisms

operating at the interfaces, as well as technological importance, and (b) it is pos-

sible to grow them experimentally with a great precision. They provide a set of

systems where nano-structure, strain and interfaces can be used to engineer their

properties [47]. They are always coherently grown, that is, lattice matched, and their

lattice constant is controlled by that of the substrate. At the fundamental level, prop-

erties of superlattices depend on (a) competition between the structural instabilities

of the individual component systems, for example, in BaTiO

W CaTiO

superlat-

tices, BaTiO

and CaTiO

have ferroelectric and anti-ferro-distortive instabilities as

the dominant structural instabilities, (b) local out-of-plane strain (relaxation of the

inter-planar distances) arising from the lattice and elastic mismatch between the two

components, (c) chemistry of the individual components and corresponding elec-

tronic band off-sets, (d) electrostatics of the systems, for example, KNBO

W BaTiO

superlattices have atomic planes with different polar character, (e) broken inversion

symmetry in certain type of superlattices, for example, a tri-component superlattice.

6 Theory of Ferroelectricity and Size Effects in Thin Films 221

−0.4 −0.2 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6

(degree)

Misfit strain

(%)

Monoclinic

phase

Tetragonal

phase

Fig. 6.7 Rotation of polarization in BaTiO

WSrTiO

superlattice as a function of epitaxial strain.

The superlattice transforms from a tetragonal ferroelectric phase to a monoclinic ferroelectric phase

at the epitaxial strain of 0:75% [reprinted Fig. 6.6 with permission from Leejun Kim, Juho Kim,

Umesh V. Waghmare, Donggeun Jung, and Jaichan Lee, Phys. Rev. B 72, 214121 (2005), copyright

(2005) by the American Physical Society]

In addition, the epitaxial strain imposed by the substrate controls properties of su-

perlattices [48].

We illustrate inﬂuence of epitaxial strain on properties of 1:1 superlattice of

BaTiO

W SrTiO

(see Fig. 6.7)[49]. While SrTiO

is not a ferroelectric, this su-

perlattice exhibits polar distortions with polarization comparable to that of bulk

BaTiO

for compressive and tensile in-plane epitaxial strains, and a minimum value

at the strain of 0:5%, where there is a structural transition from tetragonal to a

monoclinic phase, evident in rotation of polarization from the one along z-axis to

the one which is tilted toward the plane of the substrate as the strain changes from

222 U.V. Waghmare

compressive to tensile type. This structural transition at " D0:5% is accompa-

nied by softening of optical phonon and a consequent divergence in the dielectric

response of the superlattice. Interestingly, the dielectric response peaks at the epitax-

ial strain when the polarization is minimum (the point of transition). This example

shows that an optimal value of epitaxial strain for one property may not be the same

for other properties!

First-principles simulations [47, 48] show that the local electric dipole along

z-axis is often fairly uniform across the superlattice, even when one of the

component-compounds is not ferroelectric. It can be readily understood using

arguments in electrostatics. Basically, r:P is energetically very expensive and not

favorable. This relates to the fact that long wavelength LO modes (for which, r:P

is nonzero) have much higher frequency, that is, higher energy cost, than the TO

modes (for which, r:P D 0). Hence, any variation in P

along the axis of the

superlattice (z-axis), which corresponds to excitation of an LO phonon, is expected

to be weak. Similarly, if there is an in-plane component of polarization in a super-

lattice, that is expected to exhibit dependence on the layer (like being a low-energy

TO phonon). Another argument to help understand such properties of superlattices

is based on polarizability of the paraelectric component [50]: the depolarization

ﬁeld inside the ferroelectric component is very small when the polarizability of

the paraelectric component is large, hence polarization along z-axisisfavoredin

superlattices with a paraelectric layer of high polarizability.

Finally, we comment on understanding the dependence of properties of su-

perlattices or thin ﬁlms on epitaxial strain. Not all ABO

perovskites exhibit

properties with a strong dependence on epitaxial strain [51]. The indicators of great

sensitivity of properties to epitaxial strain are (a) the difference between elastic con-

stants C

–C

should be as small as possible, and (b) the g

coupling between

polarization and strain [which contribute the energy of g

C :::/] should

be large. These conditions give a soft modulus for uniaxial strain, which is what

crucially determines the variation in properties of a material with epitaxial strain.

6.2.5.3 Ferroelectricity in Nano-Thin Films of BaTiO

We now examine ferroelectric properties of BaTiO

ﬁlms sandwiched between per-

fect and realistic electrodes, with different mechanical boundary conditions, includ-

ing that of the epitaxial strain. The ferroelectric transitions and strain temperature

phase diagrams have been obtained through large-scale FERAM simulations of ﬁrst-

principles effective Hamiltonian of Ref [24]byPauletal.[27, 52], and Nishimatsu

et al. [53] and the same methodology was employed in simulating polarization

switching in epitaxial ﬁlms [Jaita-APL].

We ﬁrst discuss the size-dependent ferroelectric phase transitions in 1.6 nm thin

ﬁlm of BaTiO

sandwiched between perfect electrodes and having no epitaxial

constraint (see Fig. 6.8). Extraction of nano-size dependence of phase transitions

through MD simulations is a bit tricky, as it is well known that most simula-

tions yield ﬁnite-size–dependent phase transition behavior even for bulk materials.

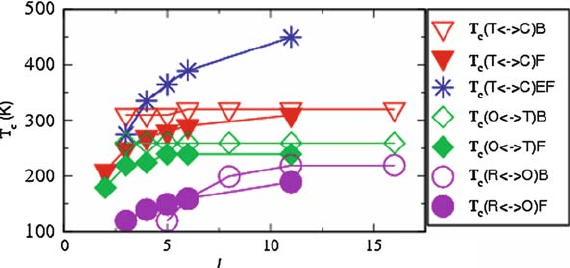
6 Theory of Ferroelectricity and Size Effects in Thin Films 223

Fig. 6.8 Size (thickness l) dependence of the transition temperatures of BaTiO

in bulk (B) form,

relaxed ﬁlms with perfect electrodes (F) and epitaxial ﬁlm with perfect electrode (EF) [reprinted

Fig. 6.2 with permission from Jaita Paul, T Nishimatsu, Y Kawazoe and Umesh V. Waghmare,

Phys. Rev. Lett 99, 077601 (2007), copyright (2007) by the American Physical Society]

Typically, a ﬁlm consisting of L

l unit cells is simulated with FERAM code.

Comparison of results obtained for such a ﬁlm with those obtained for bulk using

the same system size allows us to extract how much of the ﬁnite size effects are truly

of the ﬁlm. We note that the presence of electrodes breaks the cubic symmetry of the

ﬁlm, even in the paraelectric phase. This manifests itself in the dielectric response

with tetragonal symmetry ."

D "

¤ "

/ of the ﬁlm in the paraelectric phase (see

Fig. 6.9a). As a result, the ﬁrst phase transition in the ﬁlm is from the cubic phase to

a tetragonal one polarized in the plane of the ﬁlm. This is followed by the transition

to orthorhombic phase with in-plane polarization and then to rhombohedral phase

at low temperatures, with a nonzero out-of-plane polarization. Among these three

transitions, the C–T and T–O transitions exhibit strong size dependence up to ﬁlm

thickness of six unit cells .2:4 nm/ and the O–R transition exhibits rather unusual

size dependence! Its size dependence in the ﬁlm is weaker than that in the bulk

and it converges slowly to large size limit only above the thickness of ten unit cells

.4 nm/. Below the thickness of 2 nm, it appears that the presence of electrodes

enhances this O–R transition temperature with respect to bulk.

Size dependence of ferroelectric phase transitions in these thin ﬁlms with no epi-

taxial constraints and vanishing depolarization ﬁeld (perfect electrodes) is indeed

intriguing. The only difference in the simulations of two systems (F) and (B) is that

in the former, the electrostatic images of the in-plane components of local dipole

moments are inverted and their interaction with all the components of local dipoles

is opposite in sign for (F) and (B). Such effects are captured neither by phenomeno-

logical theories mentioned earlier, nor by the ﬁnite temperature simulations using

strategy (I), and reﬂect the unusual screening occurring at the ferroelectric–electrode

interface.

As evident from Fig. 6.8, epitaxial ﬁlms of 4 nm thickness (EF) behave rather

differently from the free ﬁlms (F): (a) they exhibit the ﬁrst transition from cubic

to ferroelectric phase with tetragonal structure with out-of-plane polarization at a

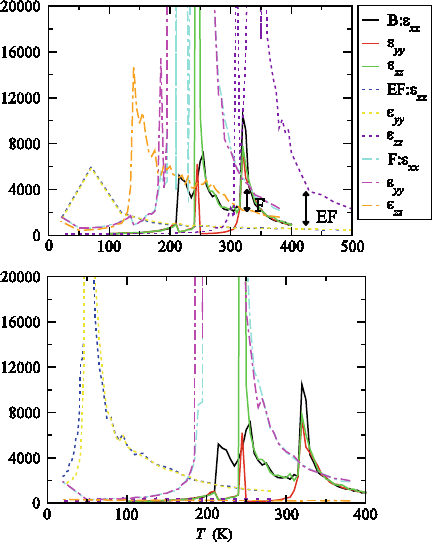
224 U.V. Waghmare

Fig. 6.9 Temperature-dependent dielectric response of BaTiO

thin ﬁlm (F), epitaxial ﬁlms (EF)

with perfect electrodes (a) and with imperfect electrodes (b), and comparison with bulk [reprinted

with permission from the PhD thesis of Jaita Paul, JNCASR (2008)]

much elevated T

.350 K/, even relative to that in the bulk, and (b) the transition

temperature exhibits a strong size dependence even at thickness of 4 nm. Second,

the transitions to ferroelectric phases with in-plane polarization occur at much lower

s. This clearly highlights the signiﬁcant role played by the mechanical boundary

conditions in controlling properties of ferroelectrics thin ﬁlms. The origin of this

lies in the fact that the coupling of strain with polarization gives rise to long length-

scale ﬂuctuations in polarization that drive the transition ﬁrst order, and by freezing

the in-plane strain, the transitions to competing phases with in-plane polarization

are suppressed, and hence T

of the transition to state with out-of-plane polarization

is enhanced. The room temperature dielectric response of both F and EF ﬁlms with

perfect electrodes is signiﬁcantly higher than that of the bulk.

To complement experimental design of epitaxial BaTiO

ﬁlms with enhanced

ferroelectric properties, Paul et al. [27] determined epitaxial strain–temperature

phase diagram using the FERAM simulations of BaTiO

ﬁlms with perfect elec-

trodes, and its size dependence (see Fig. 6.10). One learns a lot from this phase

diagram: (a) the highest temperature paraelectric to ferroelectric transition exhibits

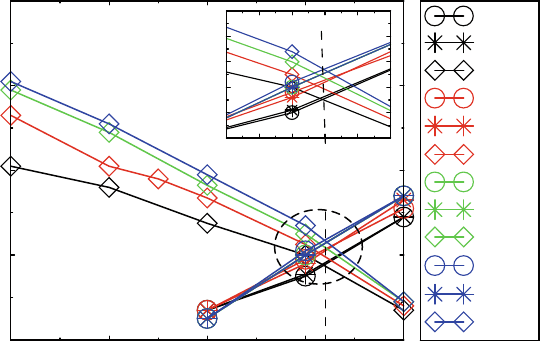
6 Theory of Ferroelectricity and Size Effects in Thin Films 225

-0.02 -0.01 0 0.01 0.02

Epitaxial Strain

200

400

600

800

(K)

l=3: T

(x)

l=3: T

(y)

l=3: T

(z)

l=4: T

(x)

l=4: T

(y)

l=4: T

(z)

l=5: T

(x)

l=5: T

(y)

l=5: T

(z)

l=6: T

(x)

l=6: T

(y)

l=6: T

(z)

0.006 0.008 0.01 0.012 0.014 0.016

III

Fig. 6.10 Thickness-dependent epitaxial strain–temperature phase diagram of BaTiO

ﬁlms sand-

wiched between perfect electrodes [reprinted with permission from the PhD thesis of Jaita Paul,

JNCASR (2008)]

the strongest size dependence; (b) ferroelectric phase with out-of-plane polarization

is most stable in the ﬁlms with compressive epitaxial strain and its stability reduces

with tensile strain; (c) the opposite is true for the ferroelectric phase with in-plane

polarization, which exhibits polarization only along [110] direction (as opposed to

the bulk, in which a ferroelectric phase polarized along [100] direction is also possi-

ble); (d) for compressive strains less than 0:5%, only the ferroelectric phase with

out-of-plane polarization is stable down to 0 K; (e) the sequence of transitions is re-

versed at the epitaxial strain of about 1.2%. At this strain, there is a crossover from

one type of R’ phase (region II) to another (region III), and we expect interesting

ferroelectric properties due to strong ﬂuctuations; (f) the size dependence of the

low-temperature transition is weaker than the one at higher temperatures.

At this stage, one wonders if one should prefer the use of epitaxial BaTiO

ﬁlms

with compressive epitaxial strain and good electrodes for applications that are based

on polarization switching, because of its high T

and large out-of-plane polarization.

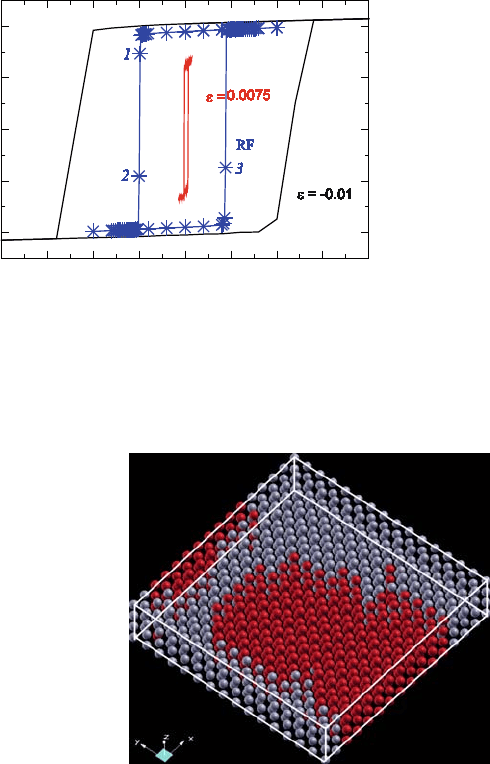
This motivated Paul et al. [54] to carry out simulations of polarization switching

with FERAM code. To investigate how polarization switching depends on the na-

ture and value of epitaxial strain, two points in the phase diagram were picked: the

one at epitaxial strain of 0:01%, and another at the strain of 0.075%. While the

former corresponds to a ﬁlm with large P

grownonGdScO

substrate, the latter

is close to the point that marks crossover from phase (II) to (III). While the T

ﬁlms with epitaxial strain of 0.0075 is much lower than the ones with the strain

of 0:01, polarization switching at T D 250 K occurs in the former at a coercive

ﬁeld of 15 kV/cm, about 30 times lower than that in the latter. Second, the remnant

226 U.V. Waghmare

polarization of the former is quite comparable to that in the bulk BaTiO

. Important

lessons to learn here are that (a) higher T

driven by strain engineering may give

the ﬁlms that are harder to switch, and (b) polarization switching is easier (at lower

coercive ﬁelds) when the ﬁlm is close to phase transition to other competing ferro-

electric phases, which act as intermediate states on the switching paths [15], with

low energy barrier. Simulation of partially relaxed ﬁlms of BaTiO

as grown in ex-

periments with DyScO

substrate (epitaxial strain of 0:013, in average sense [28],

exhibit switching at lower (by almost a factor of 2) coercive ﬁelds (see Fig. 6.11)

than the fully coherent ﬁlms, consistent with experiment. This was seen to originate

from easier formation of domains (see Fig. 6.12) in the partially relaxed ﬁlms, due

to coupling of P with ﬂuctuating in-plane strain degrees of freedom.

(mC/cm

)

E(001) (kV/cm)

-40

-1000 -750 -500 -250

-20

0 250 500 750 1000

Fig. 6.11 Polarization hysteresis in 1.6 nm-thick BaTiO

ﬁlms with epitaxial strain ", sandwiched

between perfect electrodes. Results are also given for a partially relaxed ﬁlm (RF) at the strain of

0:013 [reprinted Fig. 6.1a with permission from Jaita Paul, T Nishimatsu, Y Kawazoe and Umesh

V. Waghmare, Applied Physics Letters 93, 242905 (2008), copyright (2008), American Institute of

Physics]

Fig. 6.12 Domain of

polarization observed in

snapshot of a partially relaxed

1.6 nm-thick ﬁlm of BaTiO

just before polarization

switching occurs [reprinted

with permission from the

PhD thesis of Jaita Paul,

JNCASR (2008)]

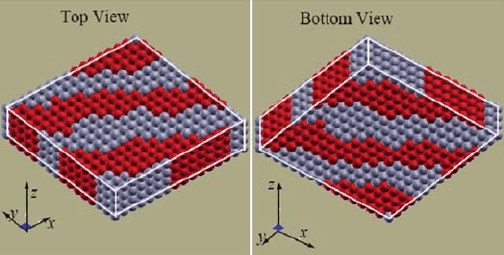
6 Theory of Ferroelectricity and Size Effects in Thin Films 227

Polarization switching in simulations based on ﬁrst-principles model Hamilto-

nian (such as the ones described here) typically occurs at much higher coercive ﬁelds

than the ones in experiment. The issues of magnitude of the coercive ﬁeld and its

size dependence, in the context of polarization switching, have been long-standing

puzzles in the physics of ferroelectrics. We point out that coercive ﬁelds predicted

from phenomenological theories are even higher than the ones in ﬁrst-principles

model-based simulations, and this is due to the neglect of spatial ﬂuctuations

of P in phenomenological theories. The origin of (a) why the coercive ﬁeld of

polarization switching is greatly overestimated in theories/simulations, and (b) why

it obeys the Kay-Dunn law .E

/ l

2=3

/ is yet to be understood. A partial an-

swer based on a phenomenological model has been given by Chandra et al. [55],

in which they consider inhomogeneous nucleation of needle-like domains at the

ferroelectric–electrode interface as the main rate-limiting step during switching.

Further microscopic evidence to support this model of domain nucleation would

help in fundamental understanding of polarization switching. Simulations described

here do not include any modes of inhomogeneous nucleation of domains that may

occur at defects at the interface with electrode, and hence the simulated coercive

ﬁelds based on homogeneous nucleation of domains here may be too high.

Ferroelectricity in BaTiO

ﬁlms with real (imperfect, d D 1 in the model) elec-

trodes is substantially different from that in the bulk, the depolarization ﬁeld being

quite strong and effective in suppressing the out-of-plane polarization. The transi-

tion to in-plane polarization is similar to that in the ﬁlm with perfect electrodes. It

occurs at around 70 K in the ﬁlm with epitaxial constraint (EF) and at 210 K in the

free ﬁlm (F), signatures of this phase transition are evident in the peaks of dielectric

response (see Fig. 6.9b). Indeed, T

for the transition to a ferroelectric phase with

in-plane polarization is comparable to that in the case of perfect electrodes, but there

is no transition at all to the phase with out-of-plane polarization. While "

is small

at all temperatures, it exhibits a broad peak around 150 K (see Fig. 6.9b). A snapshot

of local dipole moments in the low-temperature (50 K) phase (see Fig. 6.13)shows

Fig. 6.13 Striped structures of polarization domains that gets stabilized at low temperature

.T D 50 K/ in BaTiO

ﬁlms when sandwiched between real or imperfect electrodes [reprinted

with permission from the PhD thesis of Jaita Paul, JNCASR (2008)]

228 U.V. Waghmare

a phase with domains of polarization along z-direction, as was seen in experiment

[56]. Further simulations by Nishimatsu et al. [53] demonstrated that the periodicity

of this domain structure scales with the ﬁlm thickness according to l

, as predicted

by the well-known Kittel’s law.

6.2.5.4 Domains and Inhomogeneities in Ferroelectric Thin Films

Based on our discussion of (a) formation of domains in ferroelectric ﬁlms sand-

wiched between real electrodes, (b) role of domains in polarization switching, and

in the presence of thin dead layers or inhomogeneities in ferroelectrics, it is obvious

that domains play a very important role in governing properties of ferroelectrics,

particularly in the form of thin ﬁlms. Here, we argue based on fundamentals of

ferroelectric phase transitions and understand how the formation of domains in

ferroelectrics is bound to be universal and should be readily possible. It is well

established that ferroelectric phase transitions are ﬂuctuation-driven ﬁrst-order tran-

sitions. For example, in the mean ﬁeld theory analysis (which ignore ﬂuctuations),

these transitions are of the second order. Strong ﬂuctuations near such phase transi-

tions are indirectly evident in the non-analytic nature of the free energy as a function

of polarization calculated exactly from a microscopic model [39]. While overall

behavior of the free-energy function is similar to mean ﬁeld Landau free energy

(see Fig. 6.14), the states corresponding to P D 0 or small values of P for T<T

are different from the ones in Landau theory: they correspond to spatially inho-

mogeneous polarization in the system (see Fig. 6.14). This is because, when P is

constrained to values smaller than the equilibrium value below T

, a spatial ﬂuctu-

ation in P (ignored in MFT [13]) becomes critical and stable. This is essentially a

kind of domain formation! Thus, whenever there is suppression of uniform polar-

ization in a ferroelectric (below T

) due to defects or depolarization ﬁeld from the

dead layers or other deviation from the lattice, this argument suggests that domains

should spontaneously form. To capture these phenomena, it is necessary to be able

to carry out long length-scale simulations, which should be possible with FERAM

code [32].

Fig. 6.14 Exact free energy landscape of a ferroelectric as a function of uniform polarization and

illustration how a conﬁguration with inhomogeneous or domain structure (spatial ﬂuctuation in P )

becomes stable when P is constrained to be at a value other than its equilibrium

6 Theory of Ferroelectricity and Size Effects in Thin Films 229

It is also possible to understand this in terms of phonons dispersion, emphasized

in other contexts earlier in this chapter. A domain-wall of 180

type (in which the

polarization in adjacent domains is in the plane of the domain wall and anti-parallel)

is essentially a combination of long-wavelength TO phonons frozen in. These are

also unstable in the cubic structure of BaTiO

and PbTiO

[19]atT D 0 K, and can

get frozen to lower energy when uniform polarization (TO phonon at , the dom-

inant structural instability) is suppressed. For both long-wavelength TO phonons

and domains, rP ¤ 0 and there is a vanishing macroscopic ﬁeld associated with

rP D 0, indicating that both have a low energy cost. In fact, many topologi-

cal defects, such as vortices, in polarization distribution have a non-vanishing curl

P , and should readily form in the presence of defects and geometries of appropriate

nature and symmetry. These are expected to be even more abundant in thin ﬁlms

and other nano-structures of ferroelectrics, which exhibit tremendous sensitivity to

external conditions.

6.3 Summary

Ultra-thin ﬁlms of ferroelectric oxides exhibit a rich set of properties which are

sensitively dependent on the chemistry, electrical and mechanical nature of their

surrounding and to defects and inhomogeneities within (see art in Fig. 6.15). While

it is not quite possible to access all the aspects of this complexity of these ﬁlms

precisely from ﬁrst-principles theoretical analysis, it is possible to use such anal-

ysis along with modeling, phenomenological theories and experiment to obtain

fundamental insights into microscopic mechanisms operating in ferroelectric thin

ﬁlms, their length and time-scales and dependence on size. At the fundamental

level, it involves understanding how phonons and their interactions are manipulated

by various aspects of ferroelectric thin ﬁlms and their surrounding. Understanding

of mechanisms of polarization switching, dynamics of inhomogeneous polarization

order [58] and nucleation of domains are some of the challenges to be tackled by the

Fig. 6.15 An artwork to

display that polar domains

and phonons in a ferroelectric

are sensitive to various

factors, and at the heart of its

properties