Qiu X.G. (Ed.) High Temperature Superconductors
Подождите немного. Документ загружается.

Electron-doped cuprates as high-temperature superconductors 241
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
(negative magnetoresistance, Sekitani et al., 2003). These features are reminiscent
of the Kondo effect. The origin of the low-temperature upturn in T
'
cuprates can be
understood as follows. As speculated in section 6.6.1., Cu
2+
seems to be nonmagnetic
in the ideal T
'
structure with no O
ap
impurity. However, an O
ap
impurity atom
changes Cu
2+
just beneath to be magnetic, thereby giving rise to the Kondo effect.
The Kondo effect causes strong carrier scattering as well as pair breaking.
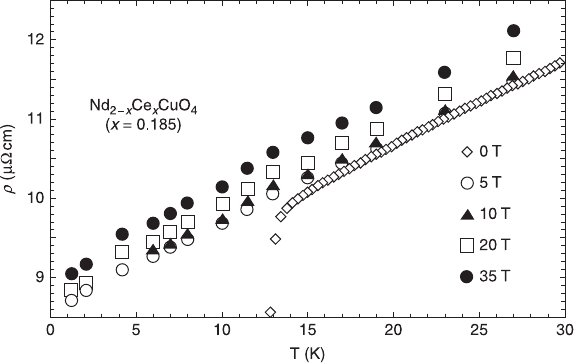
6.23 Behavior of the low-temperature resistivity under magnetic fields
in underdoped T
'
cuprates (nonsuperconducting Pr
1.902
Ce
0.098
CuO
4
(a) and superconducting Nd
1.869
Ce
0.131
CuO
4
(b) grown by MBE). The
resistivity upturn at low temperatures has a log T dependence but
saturates to a finite value toward lowest temperatures. In addition, the
upturn is suppressed in magnetic fields (negative magnetoresistance).
(Panel (a) is reprinted with permission from Sekitani et al. (2003), Phys
Rev B, 67, 174503. © 2003 by the American Physical Society.)
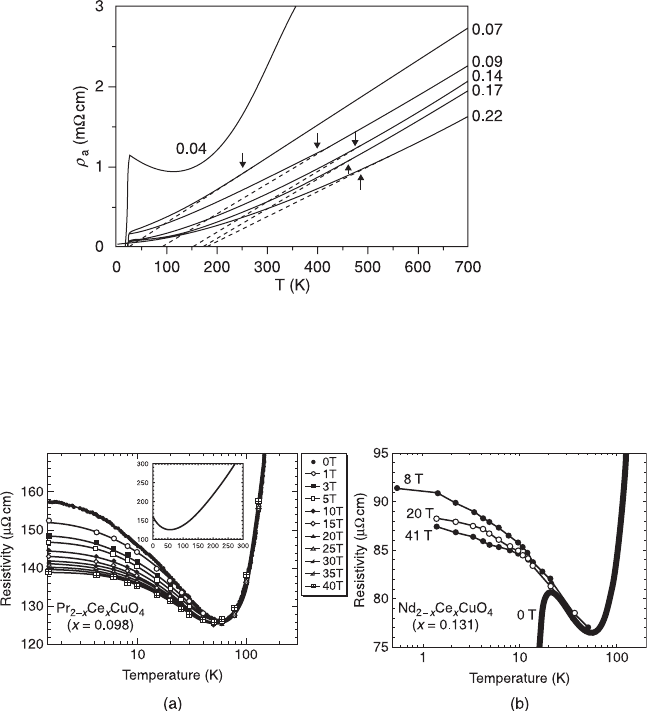
6.22
ρ
-T curves of Pr
2 – x
Ce
x
CuO
4
single crystals up to 700 K. The
specimens were given special reduction described in section 6.5.2.
The arrows indicate the crossover from a low-temperature T
2
to high-
temperature T-linear dependence. (Reprinted with permission from
Brinkmann et al. (1997), Physica C, 292, 104. © 1997 Elsevier.)
242 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
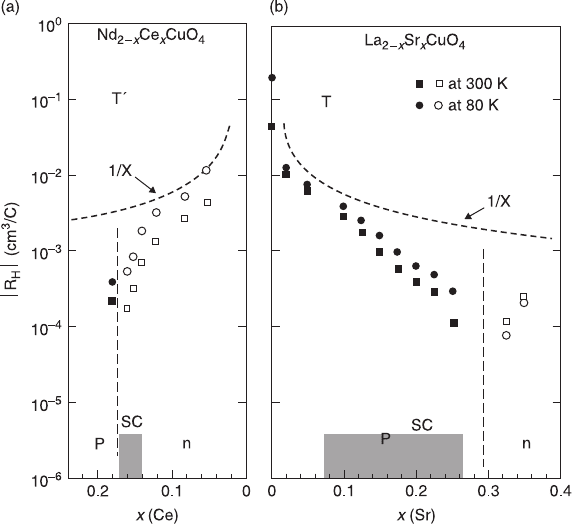
Strange behavior in resistivity is also seen in the overdoped region (Fournier
et al., 1997; Sekitani et al., 2002). In conventional metals, resistivity comes down
to a finite value (residual resistivity) at lowest temperatures. However, the
resistivity of a Nd
2 – x
Ce
x
CuO
4
film of x ~ 0.185, with superconductivity suppressed
in magnetic fields, continues to decrease almost linearly down to the lowest
temperature measured (Fig. 6.24). The absence of low-temperature saturation in
resistivity is not understood although similar behavior is seen in overdoped
Tl
2
Ba
2
CuO
6
(Mackenzie et al., 1996).
6.6.3 Hall coefficient and Seebeck coefficient
Next the Hall coefficient (R
H
) and Seebeck coefficient (S) are discussed. Both of
the coefficients represent the character of conduction careers, and are supposed to
be negative in electron conduction and positive in hole conduction. However,
such a simple view applies only to one-band semiconductors, and R
H
and S in
metals are a very complex function of the k dependent energy and relaxation time
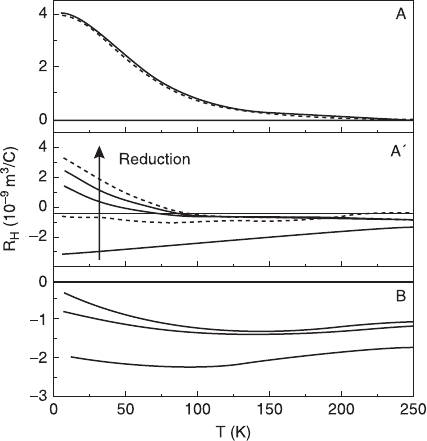
of quasi-particles (Hurd, 1972). With such circumstances in mind, we take a look
at the Hall coefficient first. Figure 6.25 shows the early result on the Ce doping
dependence of R
H
for T
'
-Nd
2 – x
Ce
x
CuO
4
, which is compared with the result for
hole-doped T-La
2 – x
Sr
x
CuO
4
(Uchida et al., 1989). The R
H
of Nd
2 – x
Ce
x
CuO
4
is
negative at x < 0.15 and becomes positive at x > 0.175. The R
H
of La
2 – x
Sr
x
CuO
4
shows an opposite change, namely positive to negative. In this early report, the R
H
follows nearly a 1/x dependence x < 0.10 in both of the compounds. The data
6.24 Behavior of the low-temperature resistivity under magnetic fields in
overdoped T
'
cuprates (Nd
1.815
Ce
0.185
CuO
4
grown by MBE). The resistivity
with superconductivity suppressed in magnetic fields continues to
decrease almost linearly down to the lowest temperature measured.
Electron-doped cuprates as high-temperature superconductors 243
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
seem to suggest that RE
2 – x
Ce
x
CuO
4
is an ‘electron-doped’ superconductor,
distinguished from the holed-doped superconductor, La
2 – x
Sr
x
CuO
4
. Even in early
reports, however, positive R
H
or positive S was sometimes reported in optimum
doped NCCO and PCCO (Wang et al., 1991; Lee et al., 1990). Furthermore it
was pointed out that R
H
of T
'
-Nd
1.85
Ce
0.15
CuO
4
shows not only a large temperature
dependence but also a large sample dependence. Later studies on transport
properties of T
'
cuprates suggested that there exist two types of careers: one
electron-like, and the other hole-like, and this led to controversy over which type
of career is crucial for superconductivity in T
'
cuprates.
The origin of the sample dependence of R
H
in T
'
cuprates was clarified from
the systematic studies varying the reduction condition to remove O
ap
impurities. It
turned out that R
H
shifts toward a more positive value with reduction.
Figure 6.26 shows the data by Brinkmann et al. (1996) for Pr
2 – x
Ce
x
CuO
4
single
crystals, which underwent ‘improved’ reduction as described in section 6.5.2.
When decreasing p
O2
during reduction, R
H
shifts towards positive. Simultaneously
6.25 Doping dependence of R
H
in electron-doped T
'
-Nd
2 – x
Ce
x
CuO
4
(a) and hole-doped T-La
2 – x
Sr
x
CuO
4
(b). The R
H
of Nd
2 – x
Ce
x
CuO
4
is
negative at x < 0.15 and becomes positive at x > 0.175. The R
H
of
La
2 – x
Sr
x
CuO
4
shows an opposite change, namely positive to negative.
(Reprinted with permission from Uchida et al. (1989), Physica C,
162–164, 1677. © 1989 Elsevier.)
244 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
the resistivity lowers and T
c
increases. Jiang et al. (1994) and Suzuki et al. (1994)
obtained similar results using Nd
1.85
Ce
0.15
CuO
4
epitaxial thin films. Moreover,
Jiang et al. (1994) reported the state of excessive reduction with superconductivity
rapidly degraded by further reduction, which was not reached in the bulk work by
Brinkmann et al. (1996). This state is identical to the one observed in superconducting
parent compounds as described in section 6.5.3. Excessive reduction eventually
makes thin films transparent and insulating while the T
'
structure is preserved. The
Seebeck coefficient shows behavior similar to the Hall coefficient, and shifts
towards a more positive value with reduction (Xu et al., 1996).
6.7 Physical properties (2) – superconducting properties
6.7.1 Tunneling
Next, the superconducting properties of T
'
cuprates are reviewed. We start by
tunneling. In most high-T
c
cuprates, no quasiparticle spectrum showing a clear
superconducting gap structure is seen in tunneling experiments. The reason is that
6.26 Reduction dependence of R
H
in Pr
2 – x
Ce
x
CuO
4
single crystals,
which underwent ‘improved’ reduction as described in section 6.5.2.
R
H
shifts towards positive with stronger reduction. Samples A and A
'
are x = 0.15 whereas sample B is x = 0.10. The p
O2
during reduction
is 0.05 mbar (solid line), 0.46 mbar (dashed line) in A, 0.05, 0.68, 1.00,
2.00, 4.00 mbar from the top in A
'
, and 0.17, 0.30, 0.45 mbar from the
top in B. (Reprinted with permission from Brinkmann et al. (1996),
Physica C, 269, 76. © 1996 Elsevier.)
Electron-doped cuprates as high-temperature superconductors 245
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
the CuO
2
networks consisting of weak Cu-O bonds in high-T
c
cuprates become
disordered at the interface, leading to severely deteriorated superconductivity.
However, a reasonably good quasiparticle spectrum has been observed in T
'
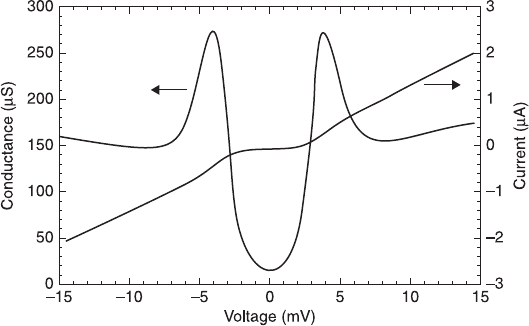
cuprates using point-contact junctions or sandwich junctions. Figure 6.27 shows
a point-contact spectrum for a Nd
1.85
Ce
0.15
CuO
4
sintered pellet (T
c
= 22 K)
obtained by Zasadzinski et al. (1992) (see also Huang et al., 1990). The spectrum
shows a clear superconducting gap structure with reasonably low zero-bias
conductance. The spectrum suggests Nd
1.85
Ce
0.15
CuO
4
to be an ‘s’ wave super-
conductor. The superconducting gap (∆) is 3.7 meV, amounting to 2∆/k
B
T
c
= 3.9,
indicating intermediate coupling like Nb. Zasadzinski et al. (1992) also derived
the Eliashberg function,
α
2
F(
ω
), by the McMillan-Rowell method (1969), which
represents the frequency-dependent interaction between electrons and bosons that
play the role of glue in Cooper pairing. Here F(
ω
) is the density of states of
bosons with a frequency of
ω
and
α
the interaction strength. The results are shown
in Fig. 6.28. One can see a good correspondence between the
ω
dependence of
α
2
F(
ω
) and the phonon density of states obtained from neutron
inelastic scattering. Then Zasadzinski et al. (1992) concluded that bosons relevant
to superconductivity in NCCO are phonons, namely NCCO is a phonon-mediated
BCS superconductor. The dimensionless electron–phonon coupling constant,
λ
(≡ 2 ∫ d
ωα
2
F(
ω)
/
ω
) is evaluated to be ~1.0, again indicating intermediate-
coupling. The T
c
as high as ~22 K in spite of
λ
~ 1.0 can be attributed to high-
frequency phonons originating from oxygen vibrations ranging up to ~100 meV.
A reasonably good quasi-particle spectrum was also obtained using sandwich
junctions, Pb/native/Nd
1.85
Ce
0.15
CuO
4
, as shown in Fig. 6.29 (Naito et al., 2000a).
6.27 Point-contact spectrum for a Nd
1.85
Ce
0.15
CuO
4
sintered pellet
(T
c
= 22 K). The spectrum shows a clear superconducting gap structure
with reasonably low zero-bias conductance. The superconducting gap (∆)
is 3.7 meV, amounting to 2∆/k
B
T
c
= 3.9. (Reprinted with permission from
Zasadzinski et al. (1992), J Phys Chem Solids, 53, 1635. © 1992 Elsevier.)

246 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
6.28 Eliashberg function,
α
2
F(
ω
), derived from the point contact spectra
in Fig. 6.27 using the McMillan-Rowell method (a, b, and c are from three
different point contact spectra). A good correspondence is seen between
the
ω
dependence of
α
2
F(
ω
) (solid line) and the phonon density of states
(dotted lines) obtained from neutron inelastic scattering. The shades
indicate the pronounced minima in
α
2
F(
ω
). (Reprinted with permission
from Zasadzinski et al. (1992), J Phys Chem Solids, 53, 1635. © 1992
Elsevier.)
6.29 Tunneling spectrum of Pb/PbO
x
/Nd
1.85
Ce
0.15
CuO
4
/SrTiO
3
(001). The
fine structures in the dI/dV curve indicated by the arrows correspond to
the pronounced minima in
α
2
F(
ω
) (Naito et al., 2000a).
Electron-doped cuprates as high-temperature superconductors 247
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
In this figure, the fine structures in the dI/dV curve indicated by the arrows
corresponds to the pronounced minima of
α
2
F(
ω
) in Fig. 6.28. The junctions were
fabricated simply by depositing Pb on an Nd
1.85
Ce
0.15
CuO
4
film. The reason why
such a simple process works was pursued by photoemission spectroscopy
(Yamamoto et al., 1997). Once NCCO films are exposed to air after growth,
oxygen atoms are adsorbed at O
ap
. Pb deposited subsequently on this surface
extracts most of the adsorbed oxygen atoms with a thin interfacial Pb layer
oxidized at the same time, resulting in a Pb/PbO
x
/NCCO junction. In this junction,
NCCO at interface is nearly free from O
ap
impurities and O1 deficiencies, hence
superconductivity is preserved at the interface. In contrast, when Pb is deposited
directly on NCCO films without air exposure, junctions show no trace of
superconductivity. This is because Pb extracts oxygen atoms at O1 instead of those
at O
ap
, making NCCO at the interface nonsuperconducting (Naito et al., 2000a).
6.7.2 Magnetic penetration depth
Magnetic penetration depth (
λ
L
) is a fundamental length scale that characterizes
superconductors as well as coherence length (
ξ
). In addition, the temperature
dependence of
λ
L
provides important information on the pairing symmetry in
superconductors. The
λ
L
(T) is related to the superfluid density, n
s
(T), by the
following equation,
[6.7]
The BCS theory for s-wave superconductors gives the following exponential
formula in the low temperature limit (Halbritter, 1971),
[6.8]
In d-wave superconductors, however, the superconducting gap ∆(k) depends
on k with ∆(k) = 0 in a certain direction. In the case of Cooper pairing via
antiferromagnetic fluctuations, the gap vanishes in ∆(k) // [110] (so called ‘line
node’), leading to
δλ
(T) proportional to T at low temperatures. Therefore the pairing
symmetry can be judged by the temperature dependence of
λ
L
(T) at low temperatures.
The first precise measurements of
λ
L
(T) were performed by a Maryland University
group in 1993 by the cavity method (resonant frequency ~9.6 GHz) using both
high-quality single crystals and epitaxial thin films of Nd
1.85
Ce
0.15
CuO
4
(Wu et al.,
1993; Anlage et al., 1994). They observed an exponential temperature dependence
for in-plane
δλ
ab
(T) at low temperatures, and hence concluded that Nd
1.85
Ce
0.15
CuO
4
is an s-wave superconductor. Moreover, they evaluated the superconducting gap
from the exponential dependence and obtained ∆(0) = 3.7 meV and 2∆/k
B
T
c
= 4.1
(assuming T
c
= 21 K). The values agree well with the values from the tunnel
experiments in section 6.7.1. A similar conclusion was also reached by Schneider et
al. (1994) and Andreone et al. (1994) almost at the same time.
248 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
In 1996, however, Cooper (1996) made one caution to the interpretation of the
experimental results of
λ
L
(T) of NCCO. He suggested that raw data need to be
corrected by the increasing susceptibility
χ
~ 1/(T +
Θ
) at low temperatures due to
Nd
3+
moments (
Θ
is 1.2 K in NCCO). The correction is simply to divide the raw
data for
λ
ab
(T) by a factor √
µ
r
––
, where
µ
r
= (1 +
χ
) is a magnetic permeability, in
the case that the sample thickness, d, is substantially larger than 2
λ
ab
. Applying
the correction to the above results from the Maryland University group, Cooper
claimed that the temperature dependence of
δλ
ab
(T) becomes T linear or T
2
at low
temperatures, indicating a d-wave superconductor. A more detailed study was
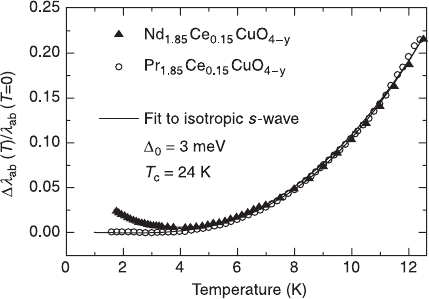
performed after Cooper’s paper when Alff et al. (1999) compared
λ
L
(T) between
Pr
1.85
Ce
0.15
CuO
4
with nonmagnetic Pr
3+
and Nd
1.85
Ce
0.15
CuO
4
with magnetic
Nd
3+
. The results are shown in Fig. 6.30. The
λ
L
(T) of NCCO is in fact anomalous
and increases below 4 K, which can be attributed to Nd
3+
moments whereas the
δλ
L
(T) of PCCO follows a simple exponential dependence. Alff et al. (1999)
concluded that both NCCO and PCCO are an s-wave superconductor with
∆(0) = 3.0 meV, 2∆/k
B
T
c
= 2.9. Experimental results appeared to converge to the
conclusion that electron-doped T
'
cuprates are an s-wave superconductor before
the results of phase-sensitive experiments were reported by Tsuei et al. (2000a).
In 2000, Tsuei et al. (2000a) claimed on the basis of their phase-sensitive
experiments (see section 6.7.3) that electron-doped cuprates as well as hole-doped
cuprates are a d-wave superconductor. This work stimulated the re-examination of
λ
L
(T). Then there emerged many experimental reports supporting d wave for T
'
cuprates. Kokales et al. (2000) repeated microwave cavity measurements and
6.30 Comparison of the temperature dependence of magnetic
penetration depth,
λ
L
(T), between Pr
1.85
Ce
0.15
CuO
4
with nonmagnetic
Pr
3+
and Nd
1.85
Ce
0.15
CuO
4
with magnetic Nd
3+
. The
λ
L
(T) of NCCO is
anomalous and increases below 4 K, which can be ascribed to Nd
3+
moments whereas the
δλ
L
(T) of PCCO follows a simple exponential
dependence. (Reprinted with permission from Alff et al. (1999), Phys
Rev Lett, 83, 2644. © 1999 by the American Physical Society.)

Electron-doped cuprates as high-temperature superconductors 249
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
Prozorov et al. (2000) employed a tunnel-diode driven LC resonator method
(resonance frequency 11 MHz), both using single crystals and thin films of PCCO
and NCCO prepared by the Maryland University group. A T
2
dependence was
observed at low temperatures in both of the experiments, which was regarded as
evidence of a dirty d-wave superconductor. However, more careful experiments
performed by Kim et al. (2003) using high-quality MBE-grown films reached a
different conclusion. In penetration depth experiments using thin films, an
interfacial deteriorated layer (typically a few hundred Å) between a substrate and a
film gives an undesired contribution. In order to eliminate such contributions, Kim
and co-workers deposited a thin buffer layer (250 Å) of nonsuperconducting
Pr
2
CuO
4
before the deposition of Pr
2 – x
Ce
x
CuO
4
. Then the
δλ
L
(T) measured by a
mutual inductance method (~ 50 kHz) clearly showed an exponential dependence
for all films of x = 0.115 ~ 0.152. In the case of T
'
films, not only an interfacial
deteriorated layer but also a surface dead layer due to O
ap
adsorption should cause
an undesired effect on
λ
L
(T). Without paying careful attention to such material
issues, one cannot reach an intrinsic temperature dependence of
λ
L
(T) of T
'
cuprates, even if a very precise measurement is performed. The author believes that
the results by Kim et al. may be the closest to the intrinsic behavior of T
'
cuprates.
Table 6.8 is a summary of penetration depth experiments on T
'
cuprates to date.
Table 6.8 Summary of the experimental results on the magnetic penetration depth
experiments for T
'
-RE
2 – x
Ce
x
CuO
4
Ref. Materials Doping level Technique s or d
Wu et al., 1993 NCCO epi-films Optimum Cavity s
Anlage by PLD
et al., 1994 NCCO single
crystals
Schenider NCCO epi-films Optimum Mutual s
et al., 1994 by PLD inductance
Andreone NCCO epi-films Optimum Ring s
et al., 1994 by PLD resonator
Alff et al., 1999 NCCO/PCCO Optimum Josephson s
epi-films by MBE current
Kokales PCCO epi-films by Optimum LC resonator d
et al., 2000 PLD
NCCO/PCCO
single crystals
Prozorov NCCO/PCCO Optimum Cavity d
et al., 2000 single crystals
Skinta PCCO epi-films Optimum Mutual s
et al., 2002a by MBE inductance
Skinta LCCO/PCCO Underdope Mutual d (underdope)
et al., 2002b epi-films by MBE to overdope inductance → s (optimum
to overdope)
Kim et al., 2003 Buffered PCCO Underdope Mutual s
epi-films by MBE to overdope inductance

250 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
6.7.3 Phase-sensitive experiments
The first phase-sensitive experiments on high-T
c
cuprates were performed in 1993
on YBCO by Wollman et al. (1993). They employed the configuration of corner
superconducting quantum interference devices (SQUIDs) (or later corner
Josephson junctions in Wollmann et al. (1995)) consisting of YBCO single
crystals and Pb, and concluded from a
π
phase shift in the magnetic field
modulation of I
c
that YBCO is a d-wave superconductor (see Fig. 6.31). Tsuei and
Kirtley (1994) employed the ring configuration containing weak-link junctions
made of YBCO films (1200 Å) deposited on tricrystal SrTiO
3
substrates (rings
are 48 µm in inner diameter, 10 µm in width). Using a scanning SQUID
microscope, they observed spontaneous magnetization of a half magnetic flux
quantum,
Φ
0
/2 = h/4e, in the 3-junction ring, but not in the 2-junction ring, which
is consistent with the behavior predicted for a d
x
2
– y
2
superconductor. Since then,
Tsuei and Kirtley (2000b) performed similar experiments for other hole-doped
systems such as Tl cuprates and Bi cuprates, etc., and they claimed the universality
of d
x
2
– y
2
superconductivity for hole-doped cuprates.
No phase sensitive experiment had been performed on electron-doped systems
until 2000. The grain-boundary Josephson current is much smaller in electron-
doped cuprates than in hole-doped cuprates, which impeded tricrystal experiments.
6.31 Top: Josephson junctions and SQUID composed of s-wave and
d-wave superconductors. Bottom: I
c
modulation in magnetic field in a
corner SQUID (a), in a corner junction (b), and in an edge junction (c).
