Qiu X.G. (Ed.) High Temperature Superconductors
Подождите немного. Документ загружается.


120 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
pseudogap line can be described as the crossover from the two-component to the
one-component (Eq. 3.4) description of the optical conductivity.
The pseudogap picture also breaks down if one looks at the energy of the dip.
Regardless of doping,
σ
1
in the pseudogap state always starts decreasing at a
similar energy, around 1200 cm
–1
(150 meV). The pseudogap, however, does
increase with decreasing doping. It becomes more and more obvious that this
feature is not the pseudogap signature.
A follow up question is why we do not see the pseudogap in the spectral weight
or
σ
1
? Why do we mostly see the nodal metal response? A qualitative answer
comes from the semi-classical conductivity formula (Ashcroft and Mermin, 1976)
[3.9]
where ν
k
and
ε
k
are the bare values calculated from band-structure for the carriers
velocity and energy, respectively.
τ
–1
(
ε
k
) is the dc scattering rate, and f is the Fermi
distribution function. In cuprates, the Fermi velocity is higher along the diagonal
(nodal) directions. Moreover, as the pseudogap opening diminishes the number of
final states to which carriers can be scattered, the scattering rate along nodal
directions also decreases. These two factors show that the integral in Eq. 3.9 has
much higher contributions from the nodal directions. Therefore, the in-plane
conductivity is looking at the nodal metal, not at the pseudogapped regions. It seems
hardly surprising, then, that no loss of spectral weight is seen as the nodal directions
are dominated by a narrowing Drude peak. This hand-waving argumentation finds
much more rigorous support in the calculations of Devereaux (2003).
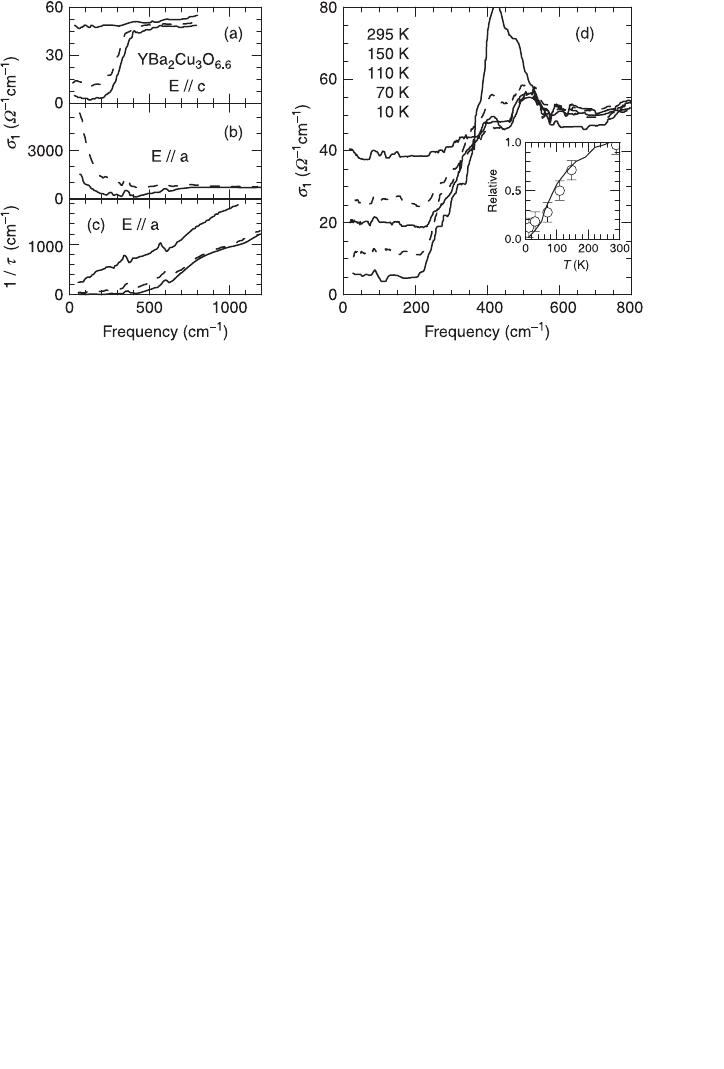
So how do we see the gap in the optical response? Look at the c-axis! Panel (d)
in Fig. 3.9 shows the optical conductivity (from which phonons were subtracted)
for underdoped YBCO along the c-axis (Homes et al., 1993). Note that the
absolute values of
σ
1
are much smaller in this direction. The high-temperature
optical conductivity does not show a Drude-like peak and it is rather dominated by
a flat incoherent background. Homes and co-workers noticed that upon cooling
the sample, low frequency spectral weight is lost, and this far above T
c
= 63 K for
this sample. Even better, as the inset of this figure shows, the spectral weight lost
scales very well with the Knight shift measured for the Cu(2) NMR line (Takigawa
et al., 1991). Once again, the calculations of Devereaux (2003) support this
picture by showing that the c-axis transport probes the antinodal (hence gapped)
regions with a stronger weight. Panels (a) and (b) of Fig. 3.9 compare
σ
1
along the
c direction and on the CuO
2
planes (Lee et al., 2005). The difference in the
energies where
σ
1
shows a pseudogap feature gives yet another evidence that
the in-plane optical conductivity is probing only the Drude response of the nodal
metal, not the pseudogap.
Although it will not be discussed here, it is interesting to point out that the
pseudogap does represent a transfer of optical spectral weight from low to high
frequencies. Hwang et al. (2008a) showed that the real part of the self-energy,
Optical conductivity of high-temperature superconductors 121
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
related to the mass enhancement (Eq. 3.6), has a pile up of states above the gap
energy associated to a loss at low energies.
As I mentioned above, the pseudogap state is accompanied by a decrease in the
scattering rate. This is the main reason why dc transport is sensitive to the
pseudogap. It is only natural, then, to look into the optical scattering rate, but we
must take extra care when doing so. Lee et al. (2005) argue that the pseudogap is
well characterized by the two component model, where carriers and bound states
are different excitations. When looking at the scattering rate, we use the extended
single component Drude model which assumes that the whole conductivity comes
from a single excitation. There is yet no clear solution for this conundrum. In this
chapter I will just ignore the contradictions and use whichever model highlights
the features of interest best. With this in mind, Fig. 3.10 (a) shows the in-plane
scattering rate for underdoped Bi2212. At room temperature it shows the marginal
Fermi liquid linear behavior. At 200 K, where the pseudogap is already open, the
low frequency scattering rate deviates from the high frequency linear behavior
defined by the dashed line. Upon cooling the material, this deviation increases.
The low frequency 1/
τ
contains the definite signature of the pseudogap. It is very
tempting to assign the energy at which the deviation from the straight line begins
to the pseudogap energy. We should restrain our enthusiasm. The data from
3.9 The panels on the left-hand side show data for underdoped
YBCO in the pseudogap regime [adapted from Basov et al. (1996)].
The dashed lines represent data in the normal state just above T
c
. The
higher solid line is the data at room temperature and the lower at 10 K.
The room temperature
σ
1
for E // a is not shown. Panel (a) shows
σ
1
along the c-axis and panel (b) along the a-axis. Panel (c) depicts the
scattering rate along the a-axis. Panel (d) shows
σ
1
for YBa
2
Cu
3
O
6.7
(T
c
= 63 K) for several temperatures [adapted from Homes et al. (1993)].
The inset compares the normalized low frequency spectral weight lost
at low temperatures (open circles) to the Knight shift for Cu(2) [from
Takigawa et al. (1991)].
122 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
Hwang et al. (2004b) shows that this energy is roughly doping independent,
contrary to the pseudogap value. In addition, panel (c) in Fig. 3.9 shows that the
scattering rate departure from linear behavior follows the energy scale in the
in-plane optical conductivity, not the pseudogap signature along the c-axis.
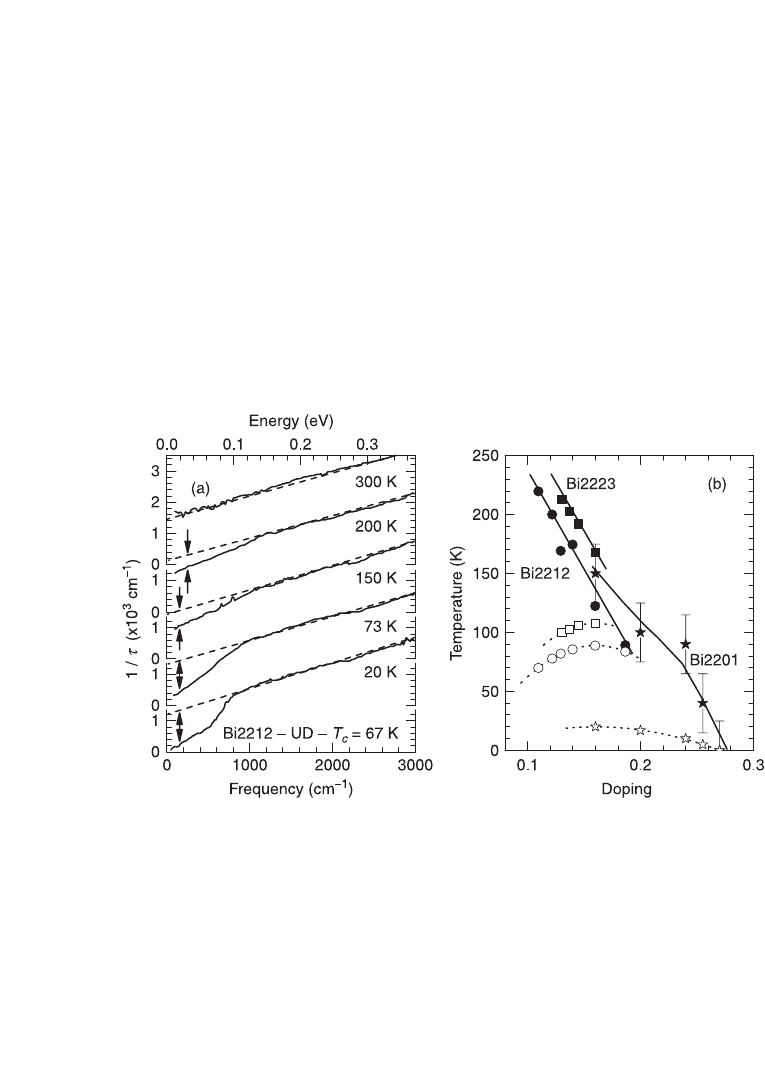
We close the pseudogap discussion comparing systems of the same family
having different number of copper oxygen planes per unit cell. Lee et al. (2005)
had already noticed that the pseudogap seems to be a property of isolated CuO
2
planes, regardless of the host material. Panel (b) in Fig. 3.10 illustrates this very
well. This figure shows the superconducting dome (open symbols) for three
different Bi-based cuprates, with one, two or three CuO
2
planes per unit cell. Data
for Bi2223 (Fujii et al., 2002) and Bi2212 (Watanabe et al., 2000) are from dc
transport. Data for Bi2201 (Lobo et al., 2009) comes from the optical scattering
rate. T
o
values for these materials are radically different and T
c
max
ranges from
20 K (one plane) to 108 K (three planes). Yet the pseudogap opening temperature
3.10 Panel (a) shows the scattering rate for underdoped Bi2212
[adapted from Hwang et al. (2004)] at several temperatures. Note that
the curves are shifted by 1500 cm
–1
and that above 1500 cm
–1
they are
indistinguishable. The dashed lines are straight lines corresponding
to their high frequency behavior. The arrows at low frequency indicate
the suppressed scattering, with respect to the linear behavior, at each
temperature. Panel (b) shows the superconducting dome and the
pseudogap opening temperatures for Bi2223 [squares, adapted from
Fujii et al. (2002)], Bi2212 [circles, adapted from Watanabe et al. (2000)]
and Bi2201 [stars, adapted from Lobo et al. (2009)]. The pseudogap for
Bi2223 is obtained from transport measurements whereas it is obtained
by several techniques in Bi2212 and by the optical scattering rate in
Bi2201.
Optical conductivity of high-temperature superconductors 123
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
seems to completely ignore the number of planes. It just follows the same line for
all families. There is a caveat here, though. Transport, dc or optical, will probe the
most conducting channels. In three-layer Bi2223 the inner plane is notoriously
underdoped, hence the above statement is only valid for the outer, more conducting,
planes.
3.4.2 From a nodal metal to a bad metal to a Fermi liquid
The optical scattering rate, which gave us a wealth of information on the pseudogap,
is also very useful in the analysis of the bad metal and the Fermi liquid regimes.
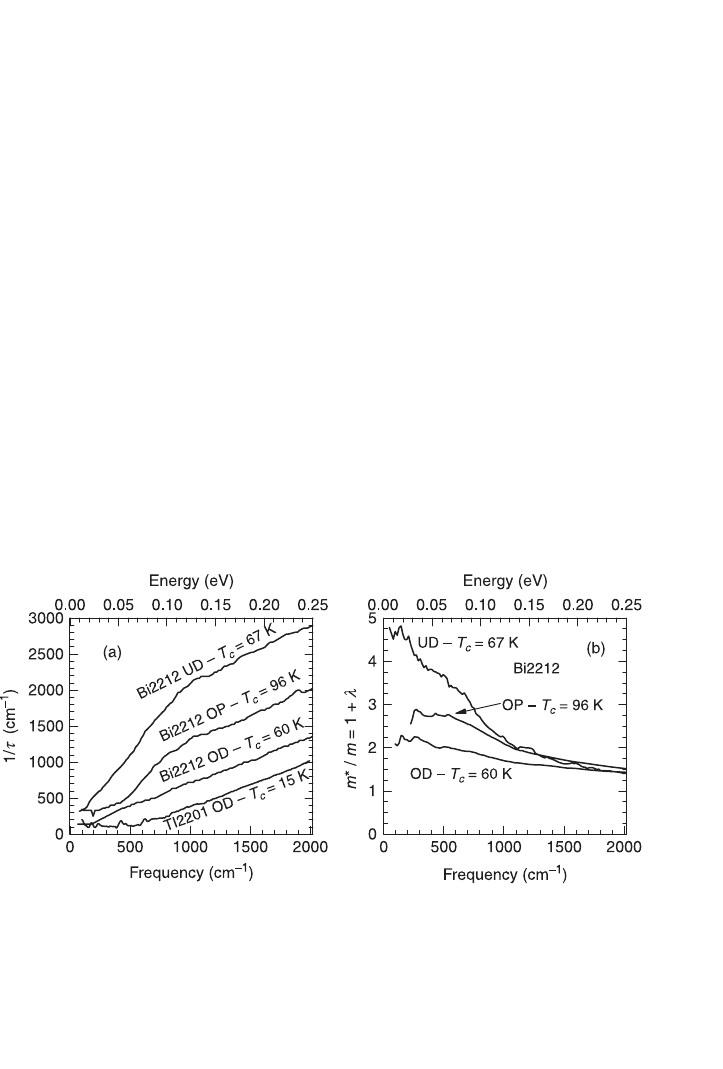
And so is the mass enhancement function. Panel (a) of Fig. 3.11 shows the optical
scattering rate for Bi2212 in the underdoped, optimally doped and lightly overdoped
regimes (Hwang et al., 2004a). It also shows 1/
τ
for deeply overdoped Tl2201 (Ma
and Wang, 2006). The normal state conductivity increases with doping. Naturally,
the absolute value of 1/
τ
decreases when moving from underdoped to overdoped.
A low frequency depletion of the scattering rate characterizes the pseudogap phase,
as discussed in the previous section. The lightly overdoped Bi2212 shows the
perfectly linear scattering rate typical of the marginal Fermi liquid response. The
scattering rate of deeply overdoped Tl2201 shows an upward curvature, reminiscent
of a more conventional Fermi liquid. However, it does not follow a
ω
2
trend but
rather
ω
1.78
. This is an important point, as this is one of the most overdoped
3.11 Panel (a) shows the optical scattering rate for Bi2212 in the
underdoped (UD), optimally doped (OP) and overdoped (OD) states,
adapted from Hwang et al. (2004a). The data are shown at 73 K for
the UD sample and 100 K for OP and OD. This panel also shows
the scattering rate for heavily overdoped Tl
2
Ba
2
CuO
6 +
δ
(Tl2201) at
90 K [adapted from Ma and Wang (2006)]. Panel (b) shows the mass
enhancement corresponding to the Bi2212 of panel (a) [adapted from
Hwang et al. (2004a)]. The critical temperatures are indicated in the
figure for all samples.

124 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
materials we know. One should not take a Fermi liquid behavior for granted at high
dopings. We are getting closer but strong electron–electron correlations are still
present.
Panel (b) of Fig. 3.11 shows the mass enhancement function for the Bi2212
shown in panel (a). At high frequencies, but below the band edge, all the curves
tend to unity, as expected. At low frequencies a clear trend develops: increasing
the doping decreases the value of m*/m. This quantity is expected to relate to the
electron–electron correlation strength. Therefore, as increasing the doping leads
to a more conventional Fermi liquid, we should find a smaller effective mass
enhancement, as shown in panel (b). But once again the one component vs. two
component approach brings trouble to the situation. Padilla et al. (2005) used the
concept that the pseudogap state is intrinsically two-component and calculated the
effective mass enhancement for YBCO. The tricky point here is that the absolute
value of the effective mass given by Eq. 3.6 depends on the plasma frequency. By
taking
Ω
p
from the Drude weight of a two-component model, Padilla et al. showed
that the effective mass remains unchanged over the full phase diagram. Such a
situation means that underdoping is equivalent to a decrease in charge density and
not in charge dressing by mass enhancement. This shows that underdoping does
not change the intrinsic properties of charges and, as pointed out by Padilla et al.,
the changes in the material properties would be due simply to the smaller volume
occupied by carriers in k space.
The one vs. two component battle is still a hot topic. It has very fundamental
implications on the physics of cuprates and the understanding of carrier behavior
in strongly correlated systems.
3.4.3 The normal state gap in electron-doped materials
Electron-doped cuprates, like their hole-doped counterparts, are materials built
across CuO
2
planes. However they lack the apical oxygen present in most hole-
doped materials. In addition, ‘electron-doped’ is almost a misnomer, as they seem
to contain electron and hole pockets in their Fermi surface (Armitage et al., 2001;
Dagan et al., 2004). From the optics point of view they are as strongly correlated
as hole-doped materials (Millis et al., 2005).
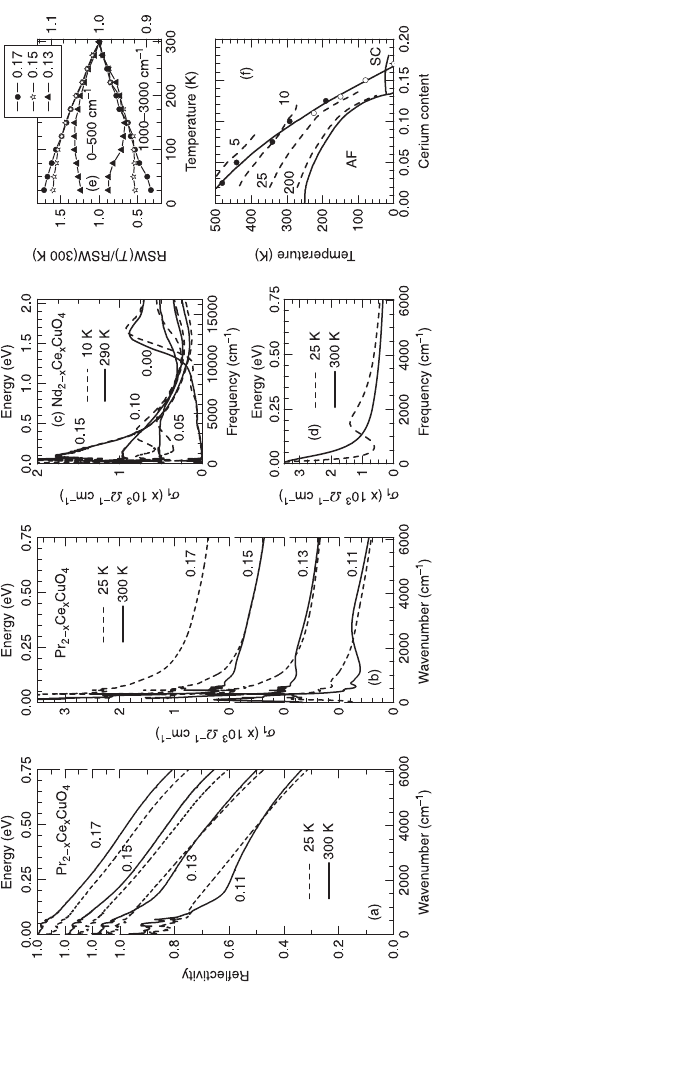
Figure 3.12 summarizes the whole situation about the optics of the normal state
gap in electron-doped cuprates. The optical response of these materials was
measured by several groups (Onose et al., 1999, 2001, 2004; Singley et al., 2001;
Zimmers et al., 2004) and there is an overall agreement on its interpretation. Here
we discuss the data from Onose et al. and Zimmers et al., Panel (a) shows the raw
reflectivity data for several dopings (from underdoped to overdoped) of PCCO at
room temperature and 25 K, which is larger than T
c
for all samples. When going
from overdoped to underdoped, the low temperature spectrum develops a dip
around 2000 cm
–1
. At the 13% and 11% Ce content samples, we can clearly observe
a crossing between low-temperature and high-temperature data around 4000 cm
–1
.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
125
3.12 Panel (a) shows the reflectivity of PCCO as a function of Ce content and temperature. Panel (b) depicts the optical
conductivity derived from the data in panel (a). Panels (a) and (b) are adapted from Zimmers et al. (2005). Panel (c)
contains the real part of the optical conductivity, measured by Onose et al. (2004), for several doping levels in NCCO.
Panel (d) is a calculation based on a local spin density wave instability for PCCO, from Zimmers and co-workers. Panel
(e), also by Zimmers et al., shows the restricted spectral weight at low frequencies and high frequencies for the PCCO
samples. Panel (f) [adapted from Motoyama et al. (2007)], shows the neutron scattering determined antiferromagnetic
phase, and the temperature where the normal state gap opens for the PCCO (open circles) and NCCO (solid circles)
data. The dashed lines are spin correlation lengths (
ξ
) and the numbers are
ξ
/a
0
, where a
0
is the lattice parameter.

126 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
Panel (b) shows the consequences of this reflectivity dip in the real part of the
optical conductivity. A dip at low frequencies slowly develops when the sample is
underdoped. In the overdoped sample the high frequency optical conductivity is
almost temperature independent. Upon underdoping, a clear overshoot of the high
frequency
σ
1
appears at low temperatures. The data for the 11% Ce sample is very
close to the density wave example shown in Fig. 3.5. This is in striking contrast to
the hole-doped pseudogap where no clear transfer from low to high frequencies is
present (see Section 3.4.1 and Fig. 3.8). The normal state gap in PCCO has a very
well characterized density wave character.
Panel (c) shows that this phenomenon is not restricted to PCCO. The NCCO
data shown has the same features as panel (b). A theoretical explanation for this,
proposed by Millis in Zimmers et al. (2004), assumed a local spin density wave
perturbation in the system. His calculations reproduce the gap opening and the
high frequency overshoot as shown in panel (d). ARPES (Armitage et al., 2001)
shows that this density wave gap opens only in a portion of the Fermi surface.
This is portrayed in the optical data by a remaining zero frequency Drude peak
even in the gapped phase. For clarity, this Drude peak is not shown in panels (b)
and (c) but the optical dc conductivity reaches values of at least 10 000
Ω
–1
cm
–1
at
low temperatures for all samples shown.
Panel (e) shows the application of the RSW (Eq. 3.8) on the data in panel
(b). In the top three curves, the integration limits are 0 and 500 cm
–1
. In the lower
three curves these limits are 1000 and 3000 cm
–1
. The RSW for these two different
integration limits are opposite, indicating spectral weight transfer between these
two ranges. They show a perfect example of a density wave gap opening. In the
overdoped sample, we only see the Drude peak growing at low frequencies at
the expense of the spectral weight in the mid-infrared. The Drude peak in the
15% Ce sample initially follows the overdoped sample. But at about 100 K this
growth slows down and the RSW saturates. Accordingly, the mid-infrared loss of
spectral weight slows down. For the heavily underdoped 13% sample we see that
the initial increase of low frequency spectral weight due to the Drude narrowing
is quickly overwhelmed by the gap opening at around 125 K and the spectral
weight decreases. Again, the mid infrared region shows the opposite of this
behavior.
Panel (f) shows the phase diagram for electron doped samples indicating the
antiferromagnetic phase, the superconducting dome and the spin correlation
length measured by neutron scattering (Motoyama et al., 2007). The gap opening
temperature for NCCO (Onose et al., 2004) and PCCO (Zimmers et al., 2004)
are superimposed on this phase diagram. It shows that the optical gap opens at a
spin correlation length of about ten unit cells. This means that the optical
conductivity is probing the short range 2D antiferromagnetic fluctuations and
it can be interpreted as the formation of a spin density wave phase. The line
defining this phase disappears inside the superconducting dome in a quantum
critical point.
Optical conductivity of high-temperature superconductors 127
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
3.5 The superconducting state
The first optical conductivity forays into the superconducting state were attempts
trying to measure the superconducting gap. This is probably one of the few topics
settled and I discuss its outcome in section 3.5.1. I will also try to tackle a
somewhat bolder question: What is the glue that binds the Cooper pairs? A series
of papers starting in the early 2000s raised the issue of kinetic energy driven
superconductivity, and this is discussed in section 3.5.2. From another front,
radical improvements in data analysis lead to the calculation of the bosonic
spectrum of excitations responsible for superconductivity. This is the central topic
of section 3.5.3.
3.5.1 Is there a gap in the superconducting optical
conductivity?
In section 3.3.4 we discussed the consequences of the superconducting transition
in the optical conductivity. The important feature is the lost area at finite
frequencies representing the superfluid weight. As a bonus we might be able to
determine the gap value. The hole-doped cuprates do not seem to come with this
bonus.
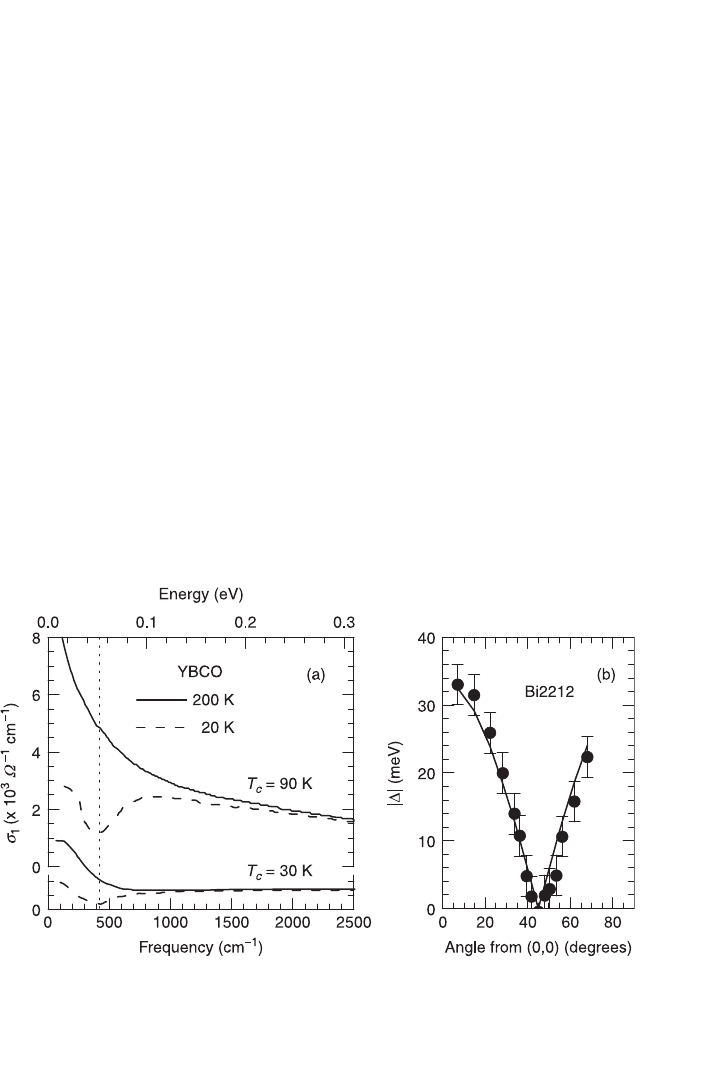
Figure 3.13 (a) shows the optical conductivity for underdoped and optimally
doped YBCO (Orenstein et al., 1990). As discussed in section 3.3.4, the gap
3.13 (a) Optical conductivity for underdoped and optimally doped
YBCO [adapted from Orenstein et al. (1990)]. The vertical line is a guide
to the eyes showing the minimum
σ
1
in the superconducting state. (b)
Gap value along the Fermi surface for optimally doped Bi2212 [adapted
from Ding et al. (1996)]. The solid line is the d-wave expectation.

128 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
value is located close to the minimum in the optical conductivity. The vertical line
shows that the minima for both compositions in the superconducting state are at
the same location. There is a debate on the value for the gap in the underdoped
state. However, this debate jumps between a gap that increases with underdoping
or a gap that follows T
c
. In fact, Le Tacon et al. (2006) showed that both energy
scales are present in underdoped cuprates, and the debate is rather which of the
two is representative of the superconducting gap. In any case, no measurement
shows a constant superconducting gap throughout the phase diagram. Two
arguments support this invisibility of the gap in the optical conductivity. The right
panel of this figure shows the gap magnitude measured by ARPES (Ding et al.
1996) for optimally doped Bi2212 as a function of the angle in the Fermi surface.
It is the typical d-wave symmetry and the gap vanishes at the Brillouin zone
diagonals (
π
,
π
). In the discussion of the pseudogap (section 3.4.1) we saw that the
optical conductivity mostly probes the nodal directions, and those are the regions
where the gap goes to zero. A second factor hampering the gap visibility comes
strictly from the electrodynamics of clean limit superconductors. Kamarás et al.
(1990) showed that optimally doped YBCO (but this is valid for hole doped
cuprates in general) is in the clean limit. Its scattering rate is at least 10 times
smaller than the gap. Figure 3.6 shows that in the clean limit, almost all the
spectral weight in the normal state is already below the gap and that the energetics
of the system is controlled by 1/
τ
. So, there is no signature in the optical
conductivity at the gap energy.
I said that that the issue was settled, but I should have said almost settled. In
some cases such as Pr-doped YBCO (Lobo et al., 2001) and the electron-doped
cuprates (Zimmers et al., 2004; Homes et al., 2006b), the system might be dirty
enough to produce a signature at the gap value.
3.5.2 Sum rules and the kinetic energy
The f-sum rule, defined by Eq. 3.7, represents charge conservation and is a
constant. However, in the framework of a single band, tight-binding, nearest
neighbor hopping model, and when written in terms of a properly chosen cut-off
ω
c
, it is a measurement of the kinetic energy of carriers:
[3.10]
where a is the in-plane lattice constant and V the unit cell volume. Equation 3.10
is valid when
ω
c
is smaller than the charge transfer energy, yet larger than the
conduction bandwidth. It is important to note that in the superconducting state,
Eq. 3.10 must include the
δ
function due to the superfluid formation. Also note the
minus sign relating the spectral weight and E
kin
.
In the superconducting state we can separate the optical conductivity into two
terms:

Optical conductivity of high-temperature superconductors 129
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
[3.11]
where the first term in the right-hand side represents the superfluid condensation
and
σ
u
1
(
ω
) is the residual conductivity due to unpaired carriers. Using Eqs. 3.10
and 3.11 we can write the superfluid weight as a function of the variation in the
kinetic energy and the differences between the normal and superconducting
optical conductivities:
[3.12]
where the superscripts n, s, and u refer to normal, superconducting, and unpaired
carriers in the superconducting state, respectively. Note that here the lower
integration limit does not include the
δ
function in the superconducting state.
Equation 3.12 also defines the quantity ∆W(
ω
c
) and shows that the comparison of
∆W(
ω
c
) to
ρ
s
gives information on the magnitude and sign of kinetic energy
changes in the superconducting transition. For simplicity in the notation, the
energies in Eq. 3.10 are measured in units of spectral weight.
BCS theory indicates that the fractional kinetic energy change at the transition
is of the order (∆/E
F
)
2
, with ∆ being the superconducting gap and E
F
the Fermi
energy (Deutscher et al., 2005). In conventional superconductors, this estimation
produces ∆E
kin
~10
–5
–10
–8
, a value much too small to be detected experimentally.
In the cuprates, the larger gap and smaller Fermi energy, leads to ∆E
kin
~10
–2
–10
–3
,
a much more manageable order of magnitude.
The first attempts to measure the kinetic energy changes across the
superconducting transition were done along the c-axis. Figure 3.14 (a) shows the
difference between normal and superconducting state spectral weight as a function
of frequency along the c-axis of underdoped Tl2201 and YBCO (Basov et al.,
2001). At high enough energies these curves, according to Eq. 3.12, should
saturate at
ρ
s
+ E
s
kin
– E
n
kin
. The dashed line in this figure is the superfluid weight
calculated from the imaginary part of the optical conductivity. In both cases it is
much higher than the saturation values for ∆W representing a FGT (section 3.3.4)
sum rule violation. Therefore, to respect Eq. 3.12, one must have E
s
kin
< E
n
kin
. The
BCS behavior states that the kinetic energy always increases in the superconducting
state (Marsiglio et al., 2006). Here, the opposite is happening. The kinetic energy
decreases when entering the superconducting state. On a second thought, despite
BCS predictions, this is finally not completely unexpected. As the coherence
length in cuprates is small, bringing carriers together increases their interaction
(potential) energy. As the total energy of the superconducting state must decrease,
the kinetic energy takes the bullet. This result, originally seen by Basov et al.
(1999), gave support for the interlayer tunneling mechanism where the
condensation energy comes from interlayer pair delocalization (Wheatley
et al., 1988). Unfortunately, the kinetic energy gain measured along the c-axis is
two orders of magnitude too small to account for condensation.
Molegraaf et al. (2002) and Santander-Syro et al. (2003) showed that the FGT
is also violated on the in-plane optical conductivity of Bi2212. Figure 3.14 (b)
