Qiu X.G. (Ed.) High Temperature Superconductors

Подождите немного. Документ загружается.

110 High-temperature superconductors

43X

small. In the cuprates,

remains ﬁnite throughout the whole spectral range. A well

behaved Drude peak, such as the one in Ag, has a Lorentzian shape and its half width

at half maximum gives the value of the scattering rate. In the cuprates the Lorentzian

peak is poorly deﬁned and the determination of the scattering rate is a more complex

task as described in Sections 3.3.2 and 3.3.3 below.

3.3.2 Two component optical conductivity

A ﬁrst attempt to reconcile the Drude model with the cuprate superconductors is

to adopt an optical conductivity composed of different types of excitations such as

[3.3]

The ﬁrst term is the Drude component (Eq. 3.2) and the sum represents a series of

bound states of resonance frequency

Ω

, intensity S

and width

. We can look at

Eq. 3.3 just as a convenient way of parameterizing the optical conductivity.

However, Quijada et al. (1999) applied the two-component approach to Bi2212

and showed that the Drude peak extracted from Eq. 3.3 explains perfectly the dc

transport properties. The magnitude of the Drude conductivity follows the inverse

of the resistivity. Most importantly, they showed that the plasma frequency

remains constant and the scattering rate of the Drude term increases linearly with

the temperature. The left panel of Fig. 3.3 shows the ﬁt obtained by Quijada et al.

at 100 K. It is composed of a narrow Drude peak and two mid-infrared bands,

3.3 Adapted from Quijada et al. (1999). The left panel shows the

measured optical conductivity (continuous line) for Bi2212 at 100 K.

The dotted line is a ﬁt using the two component approach given by

Eq. 3.3. This ﬁt is the sum of one Drude term and two mid infrared

bands shown by the dashed lines. The continuous line in the right

panel is the resistivity for the same sample (left hand scale) and the

squares are the scattering rate (right hand scale) obtained from the

Drude term in the two-component approach.



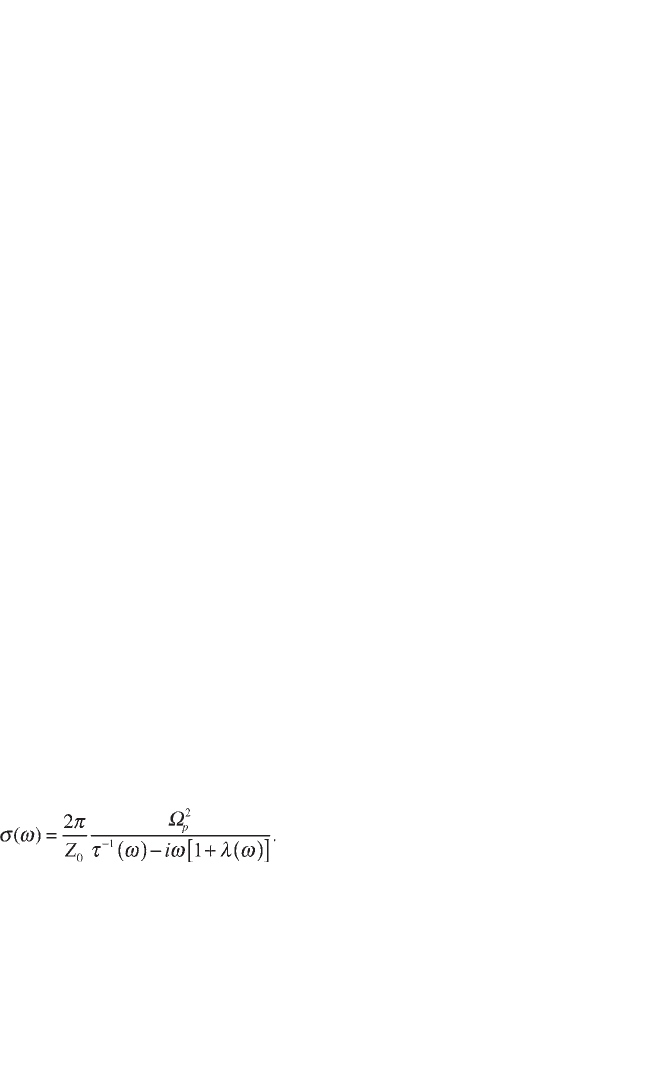
Optical conductivity of high-temperature superconductors 111

43X

shown as dashed lines. Figure 3.2 (b) shows the resistivity compared to the Drude

scattering rate. The temperature dependencies of these two quantities match

wonderfully. Finally, Quijada et al. show that the mid infrared bands have no

temperature dependence at all.

More recently, Lee et al. (2005) showed that the two component approach is a

hallmark of the pseudogap state. Looking at 10 different doping levels in YBCO,

they showed that in the pseudogap state there is a clear peak centered at zero

frequency well separated from a mid-infrared bump. They make a case for a

‘nodal metal’ where the Drude peak describes well the quasiparticles along the

Fermi arcs, which were not destroyed by the pseudogap opening. This data will be

discussed in detail in Section 3.4.

If the two-component approach produces a Drude term that correlates very well

with transport data, a clear physical meaning for the bound states is missing.

Some conjectures for the mid infrared bands include spin (Grüninger et al., 1996)

or charge (Degiorgi et al., 1995) density waves, polarons (Calvani et al., 1996;

Mertelj et al., 2000), spin-ﬂuctuations (Eom et al., 2004) and bimagnons coupled

to charges (Grüninger et al., 1999). All these propositions remain very speculative

and at this time there is no clear explanation for the mid-infrared bands of the

two-component approach. Actually, there is not even a consensus that the two-

component approach has any use beyond being a convenient parameterization of

the optical conductivity. However, we should keep in mind that the two-component

approach grasps very well the rough behavior of

3.3.3 The extended Drude model

Allen (1971) showed that a single component extended Drude model can account

for electron-phonon interactions in metals and the formalism used should be valid

for the interaction of electrons with any bosonic energy spectrum. This model is a

simple extension of Eq. 3.2 with the addition of a frequency dependency for the

scattering rate. To respect causality, the effective mass renormalization (1 +

)

also becomes frequency dependent. The optical conductivity then becomes

(Puchkov et al., 1996):

[3.4]

A frequency dependent scattering rate is equivalent to a local deﬁnition of a Drude

peak with the lifetime between collisions varying at each frequency. It does not

depend on a particular model and implies that the deviations of a Drude behavior

in the optical conductivity are a signature of electronic correlations. The extended

Drude model successfully described variegated strongly correlated systems such

as heavy fermions (Bonn et al., 1988), manganites (Takenaka et al., 2002), and of

course, cuprate superconductors (Puchkov et al., 1996). Although the modeling of

and

are important topics in condensed matter theory, the power of Eq. 3.4



112 High-temperature superconductors

43X

relies in the ability to experimentally determine the scattering rate and effective

mass from the optical conductivity. The inversion of Eq. 3.4 leads to

[3.5]

and

[3.6]

There are two pitfalls with the above equations. First, one must know the plasma

frequency

Ω

to properly determine the absolute values of these quantities. In the

absence of a well established Drude peak,

Ω

is poorly deﬁned. Always keep this

in mind when looking at absolute values of τ

–1

and λ. Second, the physical interest

of this formulation is to understand the charge carrier behavior. Hence, before the

inversion of

, it is necessary to subtract the response of the excitations that are

not related to the carriers spectrum. Examples of such excitations are phonons,

interband transitions and deep core electronic excitations. A simple subtraction

of a properly chosen constant (

∞

) from the dielectric function takes care of

eliminating the very high energy excitations. The subtraction of low frequency

excitations, such as phonons or mid-infrared bound states, is more dangerous as

one must know its spectral response.

The extended Drude model is closely connected to the concept of Fermi liquid

which predicts that in a metal of weakly interacting carriers the scattering rate

should behave as max[

, (

]. This chapter deals mostly with the frequency

behavior, and the temperature dependence will be ignored in the discussion.

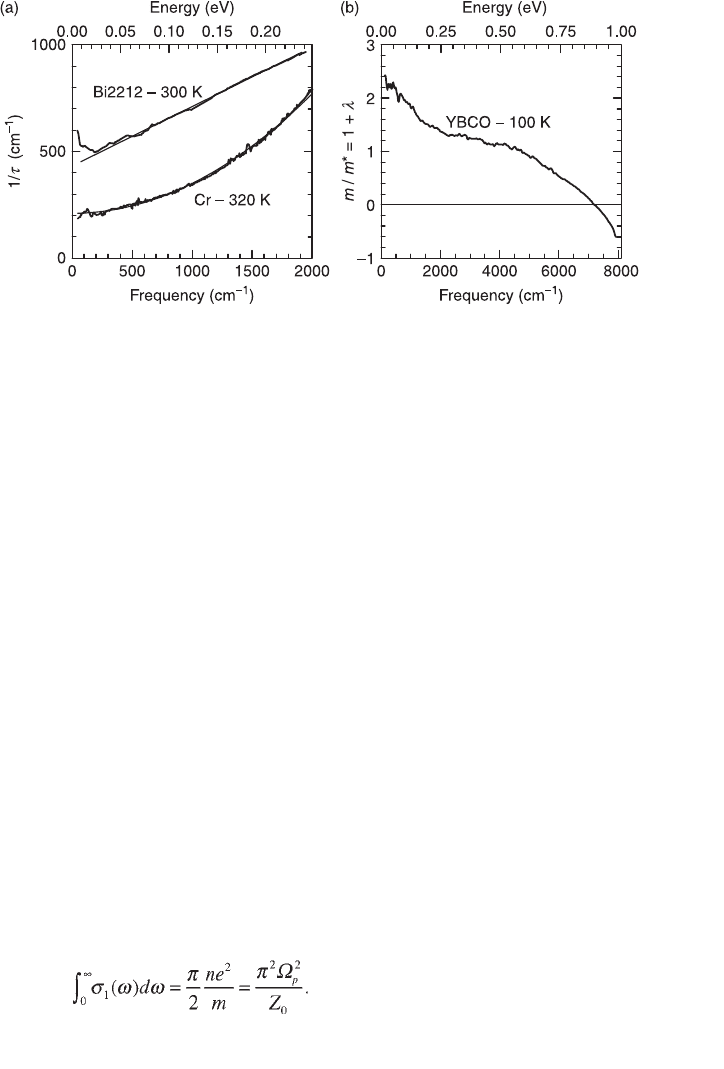
Figure 3.4 (a), shows the scattering rate for chromium (Basov et al., 2002) above

its Néel temperature. It follows a beautiful

evolution for almost two orders of

magnitude, stating the robustness of the Fermi liquid in this material. The same

ﬁgure shows the scattering rate calculated for Bi2212 at room temperature. The

Fermi liquid breakdown is obvious, with a scattering rate depending linearly on

the frequency. Based on the linear behavior of both the resistivity and the optical

scattering rate, Varma et al. (1989) proposed the marginal Fermi liquid model

(MFL). Although the nature of the bad metal normal state is still under intense

debate, the MFL provides for a simple and straightforward way to describe the

optical conductivity and can be seen as a phenomenological approach.

Nevertheless, this linear

behavior is very robust. Hwang et al. (2004b) showed

that a two component description of the reﬂectivity in Bi2212 improves when

adding a MFL-like term.

Figure 3.4 (b) shows the mass enhancement over a broad frequency range for

optimally doped YBCO at 100 K (Puchkov et al., 1996). The value of the effective

mass at zero frequency relates to the strength of electronic correlations. It decreases

with frequency and reaches a plateau having m*/m = 1 in the mid-infrared. This

means that high enough inside the conduction band, the electron–electron



Optical conductivity of high-temperature superconductors 113

43X

interaction is negligible. The sudden decrease of the mass enhancement, which

eventually becomes negative, is the signature of interband transitions. These

transitions do no represent the behavior of charge carriers and the frequency where

this feature appears indicates the upper boundary where the extended Drude model

stops giving information about the carriers.

To close this topic, it is important to note that the scattering rate and the mass

enhancement are related to the optical self energy Σ

= Σ

+iΣ

by 1/

= – 2Σ

and

ωλ

= – 2Σ

. Although the optical self-energy is averaged over the whole

Fermi surface, it is a valuable complement to ARPES (Hwang et al., 2004a). If

optics lacks the k resolution of ARPES, it has a much better signal-to-noise ratio

and energy resolution.

3.3.4 The optical conductivity sum rule and gaps in the

excitation spectrum

Charge conservation implies that the total area under

is conserved upon changes

of external parameters such as the temperature or pressure. The f-sum rule

represents this conservation:

[3.7]

When integrated to inﬁnite, n refers to the total number of electrons (including the

deep core electrons) and m to the bare electron mass. As

is a linear response

3.4 (a) Graph [adapted from Basov et al. (2002)], shows the frequency

dependent scattering rate for a Fermi liquid (chromium above its Néel

temperature). The thin line is the

behavior. The same panel also

shows the scattering rate for Bi2212 at 300 K. The thin line in this case

is the linear

behavior. (b) Graph [adapted from Puchkov et al. (1996)],

shows the mass enhancement for YBCO at 100 K over a broad energy

range.



114 High-temperature superconductors

43X

function, the conductivity for different excitations are simply added to produce

the total optical conductivity. If these excitations are decoupled, the sum rule is

fulﬁlled separately for each kind of excitation. In particular, for conduction

electrons limited to one band, one can replace the upper limit in the integration of

Eq. 3.7 by a cut-off frequency representative of the band width. In this case n and

m refer to the conduction electrons density and their effective mass.

Although there is not a straightforward relation between the density of states

(DOS) and

, the opening of a gap in the former should produce a depletion of

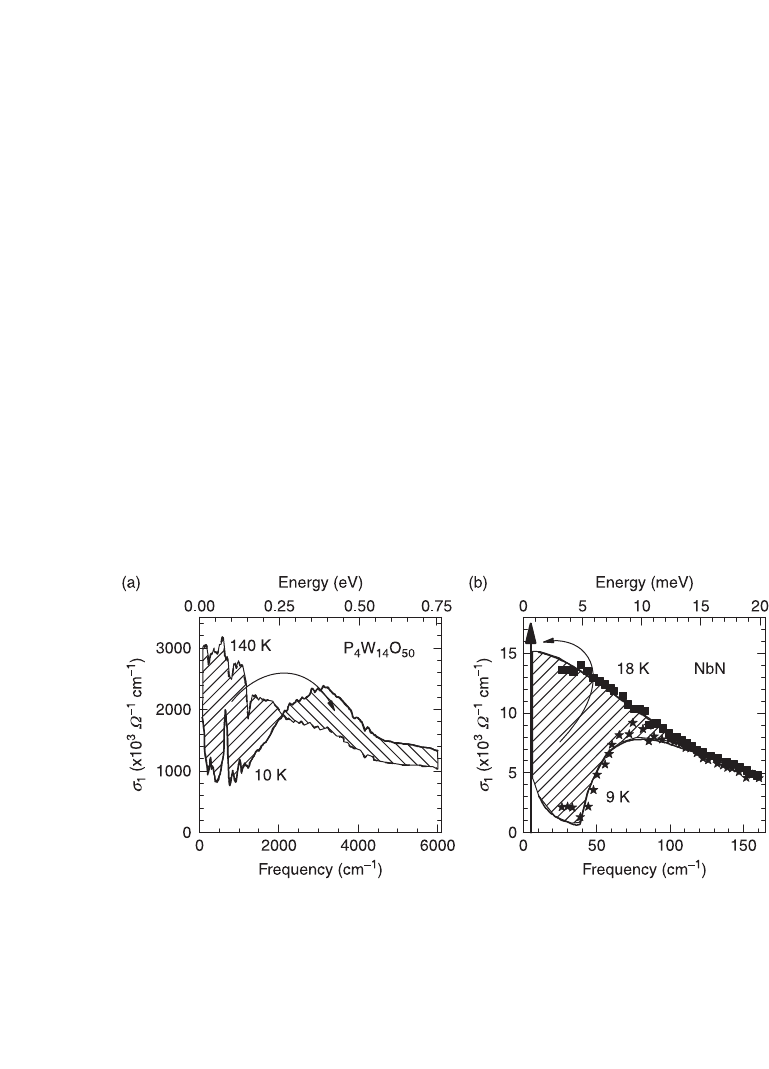
low lying states in the latter. Figure 3.5 (a) shows

for P

(Zhu et al.,

2002), which has a charge density wave (CDW) transition at 60 K (incidentally,

this material is also superconducting at 0.3 K). At 300 K there is a zero frequency

centered Drude-like peak. At 10 K, when the CDW gap (1400 cm

–1

) is fully open,

the low frequency

is depleted. Simultaneously,

increases at higher energies.

Equation 3.7 requires that the total area under the optical conductivity be

conserved. This imposes that the spectral weight lost below the gap exactly

matches the spectral weight gained above the gap energy. This is the typical

behavior of a density wave gap: transfer of low energy spectral weight to high

energies. A brief remark on the gap is that its value is close to the minimum in

rather than the crossing point between high and low temperature curves.

3.5 Panel (a) [adapted from Zhu et al. (2002)], shows the real part

of the optical conductivity for P

above and below its charge

density wave transition. Panel (b) [adapted from Somal et al. (1996)],

shows the real part of the optical conductivity above and below the

superconducting transition of NbN. The large vertical arrow is the

function representing the superﬂuid condensate. The points are the

data and the lines are either Drude or BCS isotropic gap ﬁts. In both

panels the thin arrows indicate the spectral weight transfer at the phase

transition.



Optical conductivity of high-temperature superconductors 115

43X

And what about the superconducting gap? Figure 3.5 (b) shows the optical

conductivity for the conventional superconductor NbN above and below T

(Somal et al., 1996). The opening of a superconducting gap is clearly associated

with a diminution of the optical conductivity at low frequencies. However,

opposite to a density wave gap, there is no sign of spectral weight transfer to

higher energies. Yet, Eq. 3.7 must be fulﬁlled. The zero resistivity state of a

superconducting transition is represented by a

(

) function at the origin of the

optical conductivity. It is this

function that recovers the spectral weight lost at

. This is known as the Ferrell-Glover-Tinkham (Ferrell and Glover, 1958;

Tinkham and Ferrell, 1959) sum rule.

The ability to see the superconducting gap in cuprates or not is a long standing

debate. The consensus is that ‘in a clean high-T

superconductor you do not see

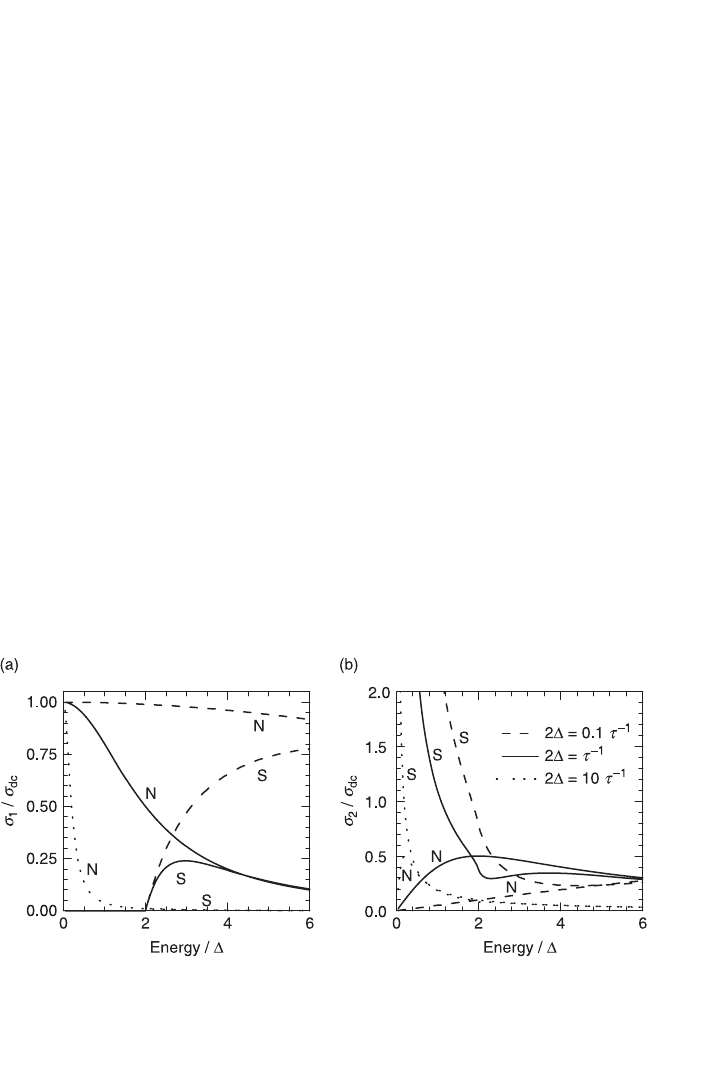
the gap’ (Kamarás et al., 1990). Figure 3.6 shows the meaning of this statement

in its left panel. The deﬁnition of clean and dirty superconductivity comes from

the comparison of the mean free path l of quasiparticles to the pairs coherence

length

. In a clean superconductor l >>

and the opposite happens in a dirty

superconductor. As l ~ v

and

~ ħv

∆ (v

being the Fermi velocity) the

conditions for clean and dirty superconductivity from the optics point of view are,

respectively,

–1

<< 2∆ and

–1

>> 2∆. The dashed curve shows the calculated

normal and superconducting

for a dirty material (Mattis and Bardeen, 1958;

Zimmermann et al., 1991). At 0 K,

vanishes for frequencies below twice the

gap. A photon of energy 2∆ can break a pair and the conductivity above the gap

will reach that of a normal metal (the factor 2 is necessary as the highest occupied

state is ∆ below the Fermi level and the lowest unoccupied state is ∆ above the

Fermi level). As

–1

is large compared to ∆, the normal state Drude peak is very

3.6 Real part (a) and imaginary part (b) of the optical conductivity

calculated for a BCS isotropic superconductor at T = 0 in the clean limit

(2∆ >>

–1

– dotted lines), the dirty limit (2∆ <<

–1

– dashed lines) and an

intermediate case (2∆ ~

–1

– solid lines). The labels ‘S’ and ‘N’ refer to

the superconducting and normal states, respectively.



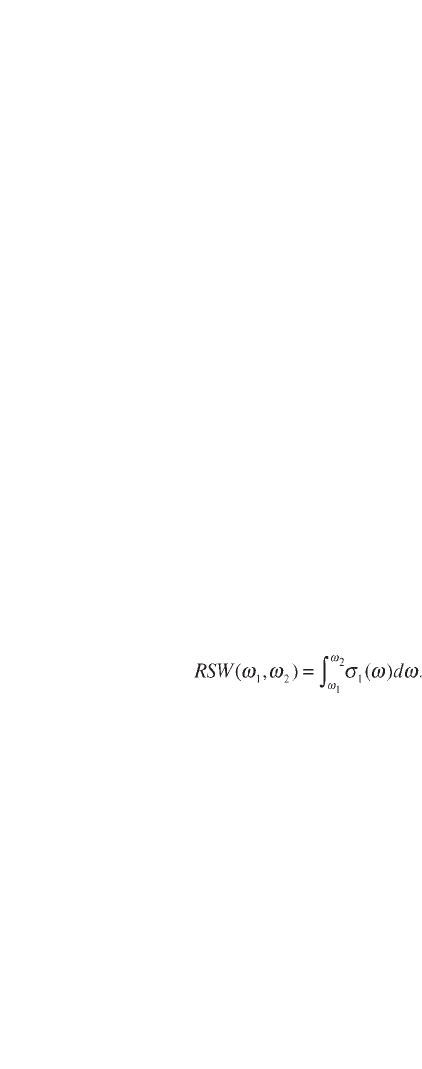
116 High-temperature superconductors

43X

broad and its conductivity is large at 2∆, almost as large as

. Thus, at the

superconducting transition, the collapse of low frequency states to the

function

will produce very marked features at 2∆ as shown by the dashed lines. The dotted

lines in this ﬁgure show what happens in the clean limit. In this case, the width of

the Drude peak is much smaller than the gap and the normal state conductivity at

2∆ is vanishingly small. Upon condensation of the Drude peak into the

function,

almost no changes in

happen. In the clean case, the superconducting

is null

everywhere but at zero frequency.

The above description leads to the key property of the optical conductivity in

superconductors: in the dirty limit

is dominated by 2∆ whereas in the clean

limit it is dominated by 1/

. It is paramount to remark that the signature of the

superconducting transition is not the observation of a gap in the optical

conductivity. The important feature is the condensation of the Drude peak into the

function and its consequent suppression of low frequency

The condensation of Cooper pairs produces dramatic changes in the imaginary

part of the optical conductivity

, as shown in the right panel of Fig. 3.6. In the

normal state,

vanishes at zero frequency and is peaked at 1/

. In the

superconducting state, because of causality relations, the

function in

produces

a (2

)

zero frequency divergence in

. By measuring the coefﬁcient of

this

–1

term, one can determine with a high degree of accuracy the superﬂuid

weight

. This is the important value from optical measurements.

3.3.5 Restricted spectral weight

It is very useful to deﬁne a restricted spectral weight (RSW) function based on

Eq. 3.7:

(3.8)

When a gap opens, the full sum rule does not make a distinction between spectral

weight transfer to high or low frequencies. The RSW function eliminates this

shortcoming.

Figure 3.7 illustrates the use of Eq. 3.8 in two hypothetical systems. Panel (a)

is a Drude metal with a scattering rate decreasing linearly with temperature. Panel

(b) starts as the same metal of panel (a) but a density wave gap opens below

150 K. The spectral weight transfer from the Drude term to the gap is taken to

increase linearly with decreasing temperature. The sum rule given by Eq. 3.7

states the areas under each curve in panel (a) and each curve in panel (b) are all

the same. Panel (c) shows an example of using the restricted sum rule with

integration boundaries of

= 0 and

(the cutoff frequency is shown in the

ﬁgure as a vertical dashed line).

When the metallic system of panel (a) is cooled, the scattering rate diminishes

which produces a narrowing of the Drude peak and an increase of the dc

conductivity. This induces a spectral weight transfer from high to low frequencies.



Optical conductivity of high-temperature superconductors 117

43X

Integration of the area under the low frequency conductivity produces, instead of

a constant value, a number that increases with decreasing temperatures (squares

in panel (c)). In the gapped material shown in panel (b), the situation is different.

At high temperatures, where by design the system is metallic, we ﬁnd the same

properties of material (a). However, below the gap opening temperature, there is

a transfer of spectral weight from low frequencies to high frequencies. Then, if we

just look at low frequencies, we see a decrease in the RWS.

An astute combined use of the sum rule and the restricted spectral weight

function goes a long way in understanding gap openings and spectral weight

transfer in conducting materials. They will come in particularly handy in the

analysis of electron doped cuprates (section 3.4.3).

3.4 The normal state

The discussion of the phase diagram (section 3.2) shows that the normal state of

cuprate superconductors has a fascinating set of exotic properties. Here I want to

discuss some speciﬁc issues that have gained a lot of interest in the past few years.

The pseudogap is such an important part of the physics of cuprates that its optical

3.7 Panel (a) shows the optical conductivity for a Drude metal where

the scattering rate decreases linearly with temperature (temperatures

shown: 300, 100, 50 and 30 K). Panel (b) is the case where the

Drude metal of panel (a) develops a density wave gap below 150 K

(temperatures shown: 300, 150, 75, 50 and 30 K). The spectral weight

transfer from the Drude peak to the gap is assumed to increase linearly

with decreasing temperature. Panel (c) shows the relative spectral

weight integrated from 0 to

for the model materials shown in panels

(a) and (b). The vertical dashed line in panels (a) and (b) indicates the

value chosen for



118 High-temperature superconductors

43X

behavior is discussed in detail in section 3.4.1. The topic discussed in section

3.4.2 covers the general optical signatures when moving from the pseudogap state

towards the overdoped regime. Section 3.4.3 makes a special discussion on the

normal state gap in electron-doped materials.

3.4.1 The pseudogap in the optical response

Besides being a spin gap, the pseudogap also represents an equally strong gap in

the charge excitation channel. However, the pseudogap is only a partial gap at the

Fermi level. By partial gap, one has to understand that there are directions on the

Brillouin zone where the Fermi surface survives and other directions that show no

states at the Fermi energy. ARPES showed that below T* the antinodal directions

are gapped and the nodal directions are metallic. This observation led to the term

‘nodal metal’ to describe the pseudogap state. The ﬁrst question to address then is

what happens to the optical conductivity.

If states are lost at the Fermi level, the low frequency optical conductivity

should decrease. In section 3.3.4 we discussed what happens for a density wave

and for a superconducting gap. In both cases, ﬁnite low frequency spectral weight

is lost. The difference between the two situations is the ﬁnal destination of this

spectral weight (either high frequencies or the

(

) function). But, again, low

frequency spectral weight is lost in the two situations. Therefore, it is natural to

look for such an effect in the pseudogap state.

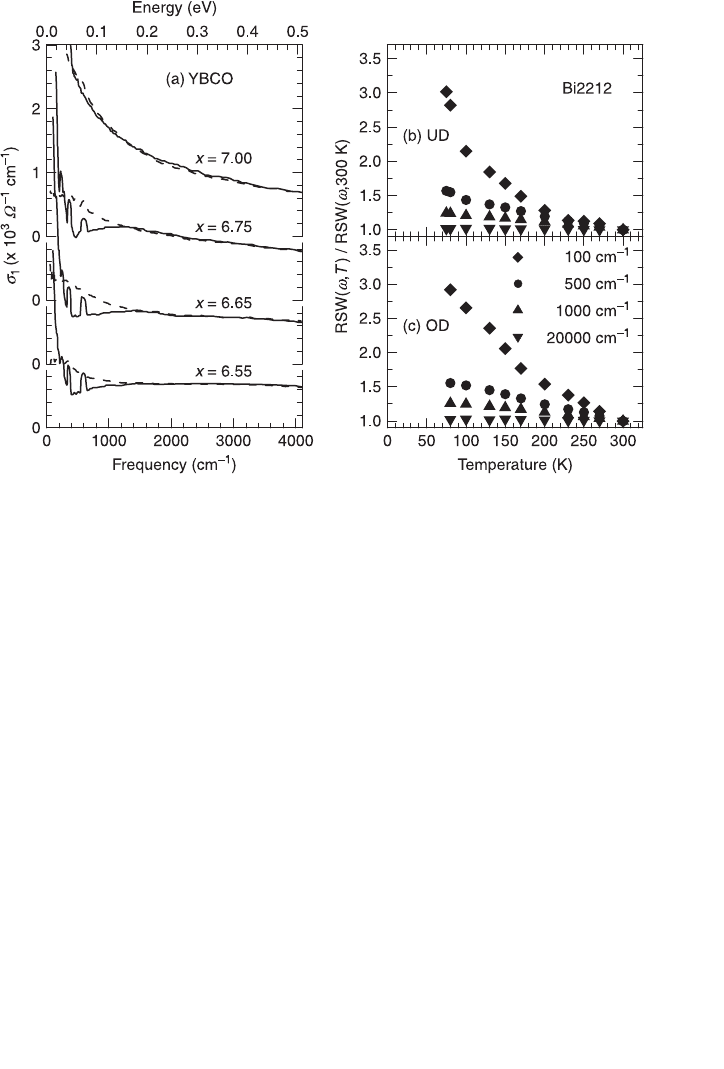
Panel (a) of Fig. 3.8 shows the real part of the optical conductivity for four

different dopings in YBCO ranging from slightly overdoped to heavily underdoped

(Lee et al., 2005). This data is measured with the electric ﬁeld of light lying on the

CuO

planes. The room temperature spectra is shown as dashed lines for all

samples. It shows the Drude-like peak observed in the strongly correlated cuprates.

The zero frequency limit of these data decreases when going towards the

underdoped side, as expected by the higher dc resistivity in this region. The shape

of all curves are nevertheless similar. The solid line in these ﬁgures show the

optical conductivity in the normal state just above T

. One common characteristic

is that for all samples the zero frequency limit of

increases. This increase

follows very well the decrease in the resistivity. The striking difference between

the near optimal doped (x = 7.00) sample and all the underdoped samples is the

dip around 500 cm

–1

. On ﬁrst sight, we would say that this is the normal low

frequency loss of spectral weight due to the pseudogap. This is not the case! As

we discuss below, this conclusion was reached for Bi2212 (Santander-Syro et al.,

2002) but the same result is valid for all hole-doped cuprates.

The ﬁrst hint that we are not facing a spectral weight loss is that we cannot see

a gain of spectral weight at higher energies as expected for a density wave gap

(Fig. 3.5). Transfer to a zero frequency

function is most certainly not reasonable

as the system is not entering the superconducting state. Panels (b) and (c) of Fig.

3.8 shed some light on what is happening. They show the RSW for an underdoped



Optical conductivity of high-temperature superconductors 119

43X

(pseudogap present) and an overdoped (no pseudogap) Bi2212 ﬁlm. The RSW is

calculated from zero to several cut-off frequencies. The ﬁrst thing to remark is

that when the cut-off frequency is chosen at 20 000 cm

–1

(2.5 eV), the f-sum rule

is fulﬁlled, meaning that spectral weight is conserved in this range. When the cut-

off frequency decreases, the low temperature spectral weight increases. Always!

When the integration starts from zero, there is not any upper cut-off frequency

that will lead to a spectral weight decreasing with decreasing temperature. Even

more astonishing is the fact that the trend seen in the underdoped sample is similar

to the one in the overdoped sample. In the discussion of the RSW (Fig. 3.7) I

argued that such an increase of low frequency spectral weight is the hallmark of a

metallic behavior. Therefore, what we are seeing in the underdoped state is a

Drude peak getting very narrow when the temperature is decreased. There is no

gap opening and the spectral weight is conserved. Panel (a) fully supports this

picture: we can describe the low temperature

as a sharp Drude peak and a mid-

infrared band. This is probably the region where the two-component approach

(Eq. 3.3) ﬁnds its best justiﬁcation. Indeed, Lee et al. (2005) argue that the

3.8 Panel (a) shows the optical conductivity for YBCO superconducting

crystals of several dopings [adapted from Lee et al. (2005)]. The dashed

line is the room temperature data and the solid line is in the normal

state just above T

for each sample. The right-hand ﬁgures show the

RSW (integrated from 0 to the several cut-off frequencies shown in the

legend) for (b) underdoped (UD) and (c) overdoped (OD) Bi2212 ﬁlms

[adapted from Santander-Syro et al. (2002)].

