Pumping Station Desing - Second Edition by Robert L. Sanks, George Tchobahoglous, Garr M. Jones
Подождите немного. Документ загружается.

For
this example,
the
preferred pump combination
is
found
to be
three identical pumping
units—two
duty pumps
and one
standby unit.
Develop
system
head-capacity
and
pump characteristic
curves.
It is
necessary
to
establish
the
full
range
of
pumping conditions
to
select pumping units properly.
As
shown below,
the
total
dynamic head
on the
pumps varies. Assume minor
losses
between
the
reservoir
and the
hydrop-
neumatic tank
at 1.8 m (6
ft). (The minor loss estimate should
be
verified
during
the
design
of
the
booster
station piping.)
The
maximum hydropneumatic tank pressure
and
minimum suction reservoir level
is
TDH
=
HGL
13n
,,
-
HGL
res
+
minor losses.
TDH
=
(98.1
m
+ 1.5
m
+ 422
kPa
TDH =
[322
ft + 5 ft + 61
lb/in.
2
X
0.102
m/kPa)
-
100.0
m + 1.8 m
=
44.4
m X
2.31
ft/(lb/in.
2
)]
-
328 ft
+
6
ft =
146
ft
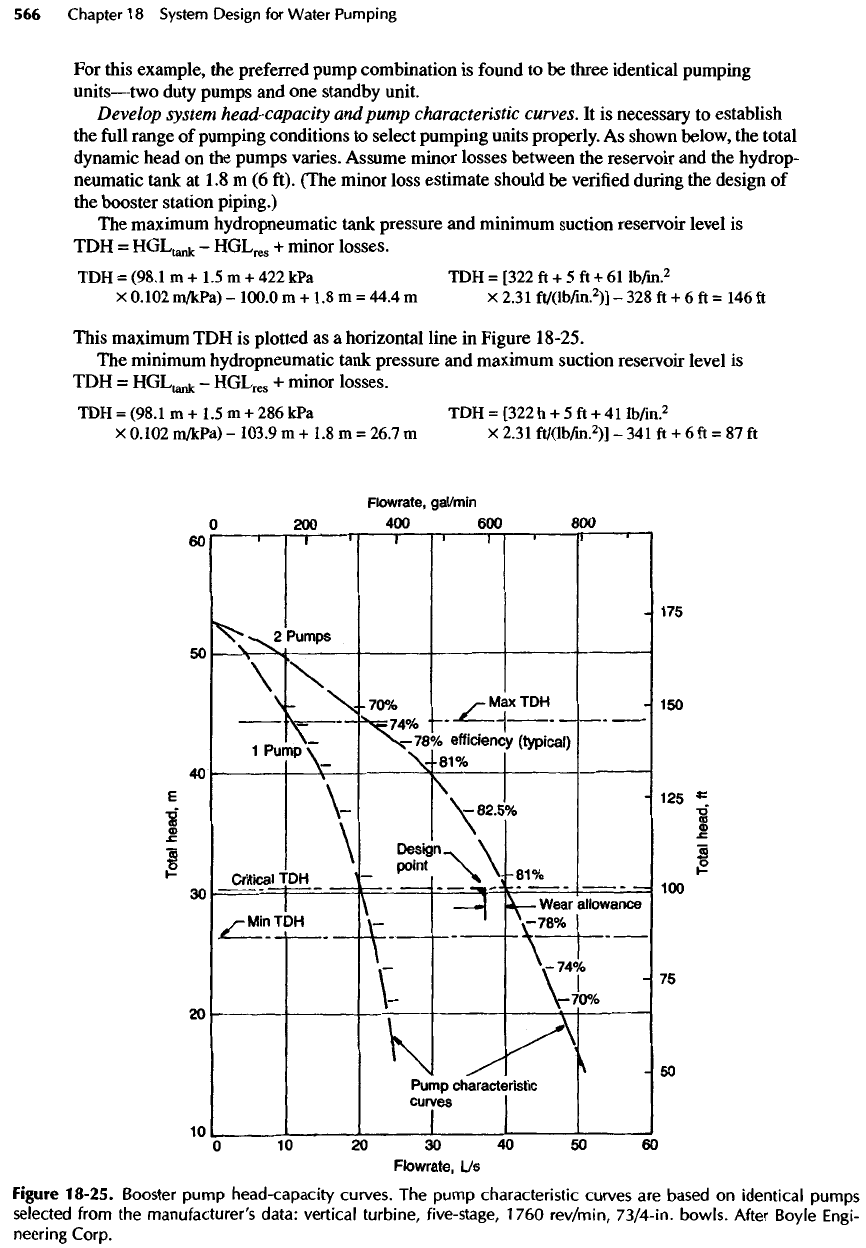
This maximum
TDH is
plotted
as a
horizontal line
in
Figure 18-25.
The
minimum
hydropneumatic tank pressure
and
maximum suction reservoir level
is
TDH
=
HGL
1
^
-
HGL
res
+
minor losses.
TDH
=
(98.1
m+
1.5 m +
286kPa
TDH =
[322h
+ 5 ft + 41
lb/in.
2
X
0.102
m/kPa)
-
103.9
m + 1.8 m =
26.7
m X
2.31
ft/(lb/in.
2
)] - 341 ft + 6 ft = 87 ft
Figure
18-25.
Booster
pump
head-capacity
curves.
The
pump
characteristic
curves
are
based
on
identical
pumps
selected
from
the
manufacturer's
data:
vertical
turbine,
five-stage,
1760
rev/min,
73/4-in.
bowls.
After
Boyle
Engi-
neering
Corp.

This minimum
TDH is
shown
as a
horizontal line
in
Figure
18-25.
The
minimum hydropneumatic tank pressure
and
minimum suction reservoir level
is
critical
because
the
suction pressure
is
minimum.
TDH =
HGL
131
^
-
HGL
res
+
minor
losses.
TDH =
(98.1
m + 1.5 m + 286
kPa
TDH
=
[322
ft + 5 ft + 41
lb/in.
2
X
0.102
m/kPa)
-
100.0
m
+ 1.8
m
=
30.6
m X
2.31
ft/(lb/in.
2
)]
- 328 ft + 6
ft
= 100 ft
This critical
TDH
(30.6
m or 100 ft) is
also shown
as a
horizontal line
in
Figure
18-25.
The
pumps
must
be
able
to
discharge
the
peak design
flowrate at
this critical TDH,
so the
"design
point"
for the
system
is 37 L/s at
30.6
m
(587
gal/min
at 100
ft).
The
next step
is to find a
pump curve that satisfies
the
following requirements when
two
such
pumps
are
operating:
•
Operate with acceptable
efficiency
(70%
or
better)
at
both maximum
and
minimum system
heads.
•
Operate without cavitation
at
minimum system head. Thus,
NPSH
A
must equal
or
exceed
the
NPSH
R
shown
on the
manufacturer's pump curves.
•
Operate
at the
"design
point"
increased
by a flowrate of 5 to 10% for
wear allowance.
Available pump characteristic curves
are
presented graphically
in
pump
manufacturers'
catalogs,
and the
manufacturers' sales representatives should
be
consulted
to
assist designers
in
the
selection
of the
best-suited pumps.
A
sample pump characteristic curve that satisfies
the
design requirements
is
plotted
in
Figure
18-25
for one
pump
and for two
pumps operating
in
parallel.
The
electric motor must
be
able
to
drive
the
pump
at any
combination
of
head
and
discharge
from
the
maximum
to the
minimum TDH.
The
maximum required power
can be
found
by
trial,
but
pump
manufacturers'
catalogs usually show
the
point where
the
power demand peaks.
For
the
pumping unit
selected,
the
peak occurs
at a flowrate of
18.3
L/s
(290 gal/min)
and a TDH of
34.1
m
(112
ft) at a
pump
efficiency
of
82%. From
a
combination
of
Equations 10-6
and
10-7,
the
motor output power
is
_
qH
_
18.3
L/s
x
34.1m
_
74
.
vw
p
_
gH
_ 290
gal/minx
112 ft _
f
~
102i;
~
102x0.82
"
7
*
4C>KW
^
~
3960"E^
~
3960x0.82
"
1U
'
U
hp
Determine
the
required
hydropneumatic
tank
capacity.
The
operation
of a
hydropneumatic
tank
is
based
on the
following relationship
(if
constant temperature
is
assumed):
P
1
V
1
=
P
2
V
2
(18-2)
where
P is the
absolute pressure,
V is the
volume
of
air,
and the
subscripts
1 and 2
indicate ini-
tial
and final,
respectively.
A
hydropneumatic tank
is
typically designed
to be at
least
10% filled by
water
at the
mini-
mum
station pressure.
The
tank volume
is
normally selected
to
limit pump cycling
to 4 to 6
cycles
per
hour.
For
this problem, assume
a
minimum volume
of 10% and a
maximum
of 5
cycles
per
hour.
Select
the
following
pump operational
criteria:
•
First pump
on
when tank pressure
falls
to 314 kPa (45
lb/in.
2
)
or
32.0
m
(104
ft) WC
•
Second pump
on
when tank pressure
falls
to 286 kPa
(41
lb/in.
2
)
or
29.2
m (95 ft) WC
•
Second pump
off
when tank pressure
rises to 394 kPa (57
lb/in.
2
)
or
40.2
m
(132
ft) WC
•
First pump
off
when tank pressure
rises to 422 kPa (61
lb/in.
2
)
or
43.0
m
(141
ft) WC.
Both one-
and
two-pump operations need
to be
analyzed
to
determine which governs
the
size
of
the
hydropneumatic tank.
The
minimum hydropneumatic tank volume
for the
one-pump
operation
is
found
as
follows:
Determine
the
percentage
of
tank water volume used
in the
one-pump operation, that
is, the
pressure change
from
314
kPa (45
lb/in.
2
)
gauge
to 422 kPa (61
lb/in.
2
)
gauge.
The
tank water

volume
at
minimum pressure
286
kPa
(41
lb/in.
2
)
gauge
was
previously assumed
at
10%. Atmo-
spheric pressure (see Table
A-6 or
A-7)
is 101 kPa
(14.7
lb/in.
2
)
at the
site. From Equation 18-2,
(286
+
101)
kPa X
(100
- 10) (41 +
14.7)
lb/in.
2
X
(100
- 10)
=
(314
+
101)
kPa X
(100
- %
water)
= (45 +
14.7)lb/in.
2
X
(100
- %
water)
At
314
kPa, water
=
16.1%
At 45
lb/in.
2
,
water
=
16.0%
(286
+
101)kPa
X
(100
- 10) (41 +
14.7)lb/in.
2
X
(100
- 10)
=
(422
+
101)kPa
X
(100
- %
water)
= (61 +
14.7)lb/in.
2
X
(100
- %
water)
At
422
kPa, water
=
33.4%
At 61
lb/in.
2
,
water
=
33.8%
Volume used
=
17.3% Volume used
=
17.8%
Determine
the
average capacity
of the
single-pump operation varying between
its on and off
points. Assume
the
suction reservoir
is at its
maximum operating level [water
surface
elevation
=
103.9
m
(341
ft)],
because this results
in
increased pump discharge (reduced TDH)
and is
therefore
a
critical case
for
hydropneumatic tank sizing.
The
hydropneumatic tank pressure
for
the
one-pump operation varies
from
314
kPa (45
lb/in.
2
)
to 422 kPa (61
lb/in.
2
).
The
average
tank
pressure
is 368 kPa (53
lb/in.
2
).
The
average one-pump
TDH is
calculated
as
follows
(see
Figure
18-26):
TDH
=
98.1
m
+ 1.5
m
+
(368
kPa TDH = 322
ft
+ 5
ft
+ [53
lb/in.2
X
0.102
m/kPa)
-
103.9
m + 1.8 m X
2.31
ft/(lb/in.2)]
=
35.0m
-341ft
+
6ft=115ft
From
the
one-pump curve (Figure 18-25),
the
pump capacity (new)
for a TDH of
35.0
m
(115
ft) is
18.0
L/s
(286
gal/min).
Determine
the
hydropneumatic tank minimum volume using
the
following relationship: mini-
mum
volume
=
1
I
2
pump capacity
x
1
I
2
cycle time/portion
of
tank used (expressed
as
decimal):
Minimum volume
=
V
2
X 18 L/s X
V
2
Minimum volume
=
V
2
X 286
gal/min
X
V
2
X
720
s/0.173
=
18,700
L X 12
min/0.178
=
4820
gal
Determine
the
percentage
of
tank water volume used
in the
two-pump operation:
(286
+
101)
kPa
X
(100
- 10) = (41 +
14.7)
lb/in.
2
X
(100
- 10) =
(394
+
101)
kPa
X
(100
- %
water)
(57 +
14.7)
lb/in.
2
X
(100
- %
water)
Percentage
water
at 394 kPa =
29.6%
Percentage
water
at 57
lb/in.
2
=
30.1
%
Volume used
=19.6%
Volume used
=20.1%
Determine
the
average capacity
of the
second pump operating between
its on and
off
points
with
the first
pump operating continuously. Again assume
the
suction reservoir
is at its
maxi-
mum
operating level [water
surface
elevation
=
103.9
m
(341
ft)].
The
hydropneumatic tank
pressure
for the
second pump operation varies
from
286 kPa (41
lb/in.
2
)
to 394 kPa (49
lb/in.
2
).
The
average second pump
TDH is
calculated
as
follows
(see Figure
18-26):
TDH =
98.1
m + 1.5 m +
(340
kPa TDH = 322 ft + 5 ft + [49
lb/in.
2
X
0.102
m/kPa)
-
103.9
m X
2.31
ft/(lb/in.
2
)]
- 341 ft
+
1.8m
=
32.2m
+
6ft=105ft
From
the
one-pump curve (Figure
18-25),
the
capacity
of the
second pump
for
a
TDH of
32.2
m
(105
ft) is
19.2
L/s
(304
gaVmin).
Determine
the
minimum hydropneumatic tank volume
for the
operation
of the
second pump:
Minimum volume
=
V
2
X
19.2
L/s
Minimum volume
=
V
2
X 304
gal/min
X
V
2
X 720
s/0.196
=
17,600
L X
V
2
X 12
min/0.201
=
4540
gal
Thus,
the
minimum hydropneumatic tank volume
is
18,700
L
(4820 gal)
as
determined
by
sin-
gle-pump
operation.
Because
the
system
is
vulnerable
to
power outages, reliability relative
to
short-duration
power outages
and for
average
day
system demands could
be
improved
by
increasing
the
tank
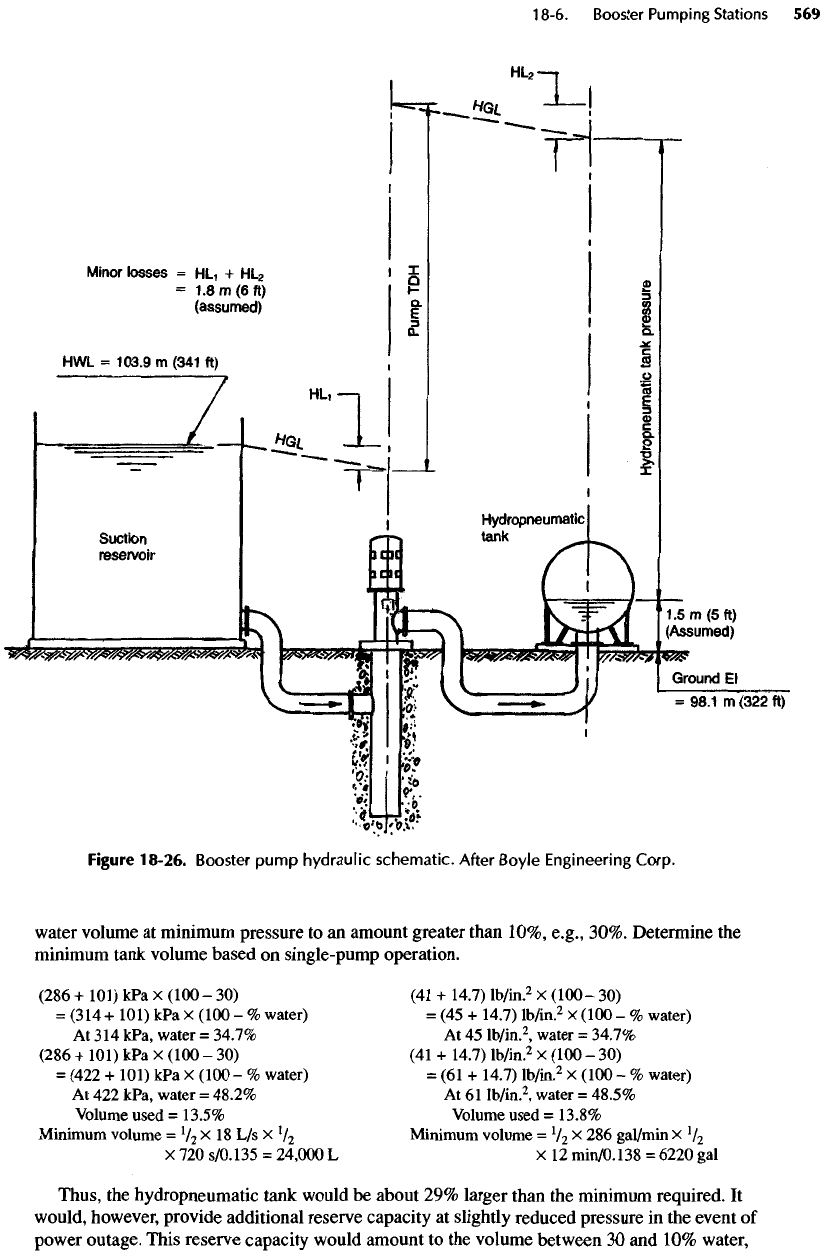
Figure
18-26.
Booster
pump
hydraulic
schematic. After Boyle Engineering
Corp.
water
volume
at
minimum pressure
to an
amount greater than 10%, e.g., 30%. Determine
the
minimum
tank volume based
on
single-pump operation.
(286
+
101)
kPa
X
(100
- 30) (41 +
14.7)
lb/in.
2
X
(100
- 30)
=
(314+
101)
kPa
X
(100
- %
water)
= (45 +
14.7)
lb/in.
2
X
(100
- %
water)
At
314
kPa,
water
=
34.7%
At 45
lb/in.
2
,
water
=
34.7%
(286
+
101)
kPa
X
(100
- 30) (41 +
14.7)
lb/in.
2
X
(100
- 30)
=
(422
+
101)
kPa X
(100
- %
water)
= (61 +
14.7)
lb/in.
2
X
(100
- %
water)
At
422
kPa,
water
=
48.2%
At 61
lb/in.
2
,
water
=
48.5%
Volume
used
=
13.5% Volume
used
=
13.8%
Minimum
volume
=
V
2
X
18
L/s X
V
2
Minimum
volume
=
V
2
X 286
gal/min
X
V
2
X
720
s/0.135
=
24,000
L X 12
mm/0.138
=
6220
gal
Thus,
the
hydropneumatic tank would
be
about
29%
larger than
the
minimum required.
It
would,
however, provide additional reserve capacity
at
slightly reduced pressure
in the
event
of
power outage. This reserve capacity would amount
to the
volume between
30 and 10%
water,
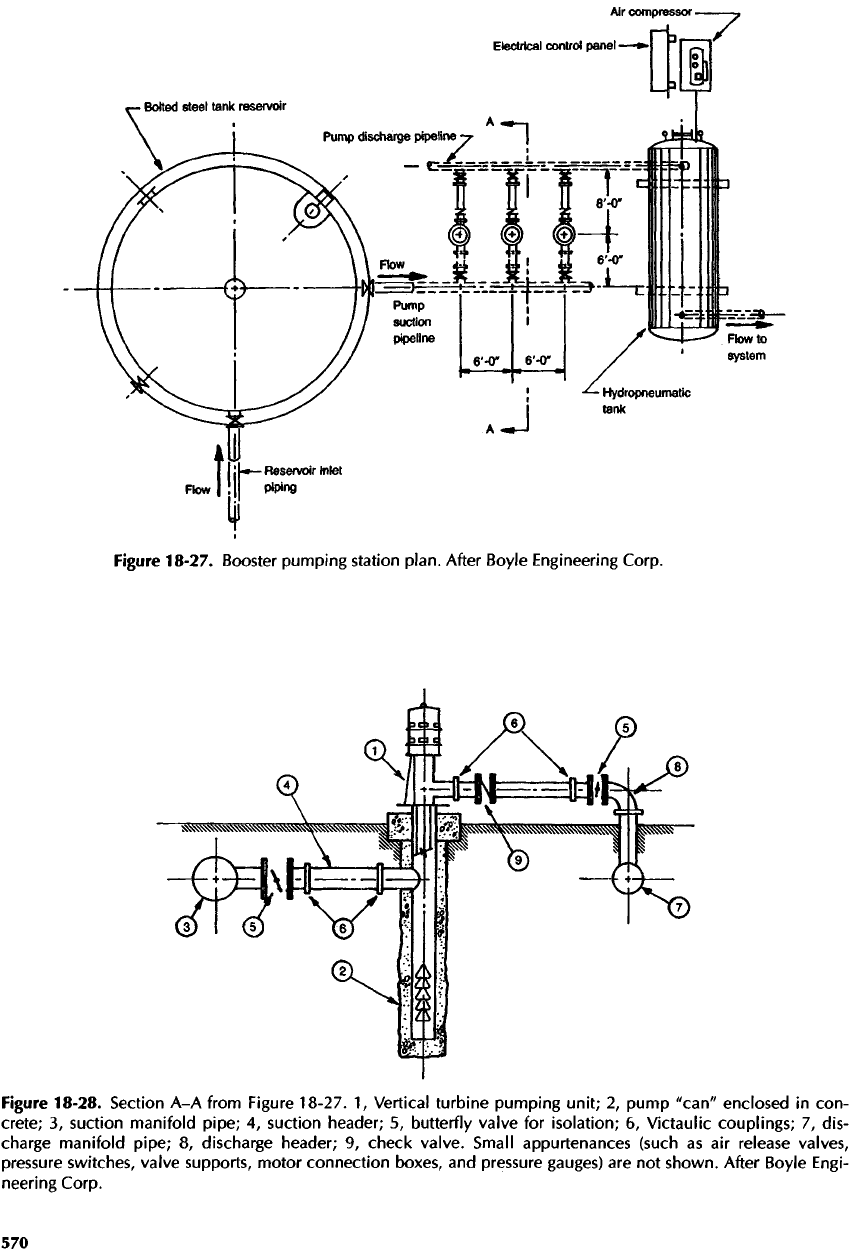
Figure
18-28.
Section
A-A
from Figure 18-27.
1,
Vertical
turbine
pumping
unit;
2,
pump
"can" enclosed
in
con-
crete;
3,
suction
manifold
pipe;
4,
suction header;
5,
butterfly
valve
for
isolation;
6,
Victaulic
couplings;
7,
dis-
charge
manifold
pipe;
8,
discharge header;
9,
check valve. Small appurtenances (such
as air
release
valves,
pressure
switches,
valve supports, motor connection boxes,
and
pressure
gauges)
are not
shown. After Boyle Engi-
neering Corp.
Figure
18-27. Booster
pumping
station
plan.
After Boyle Engineering Corp.

Packaged Booster Pumping Stations
At
least
one
manufacturer
(see Section
1
1-10,
Subsec-
tion "Multistage
Centrifugal
Pumps") markets pack-
aged
booster
pumps with built-in variable speed
controls designed
to
satisfy
demands
for
very small
to
rather large
flows for
houses, high-rise buildings,
or
subdivisions
at
little change
of
pressure. Some (but
not
all)
of the
foregoing calculations
can be
avoided
because
(1)
integrated diaphragm tanks
are
sized cor-
rectly
for the
pumps
and the
application
and (2) the
speed controls ramp
the
pump speed
up or
down auto-
matically
as
more pumps
are
switched
on and
off.
18-7.
References
1.
Metcalf
and
Eddy, Inc.
Wastewater
Engineering:
Collection, Treatment, Disposal,
and
Reuse,
2nd ed.
McGraw-Hill,
New
York
(1978).
2.
"Water
supplies
—
fire flow
tests."
Special
Bulletin
No.
42,
National
Board
of
Fire
Underwriters,
New
York (July
1958).
3.
Fair,
G.
M.,
I. C.
Geyer,
and D. A.
Okun.
Water
and
Wastewater
Engineering, Vol.
1,
Water
Supply
and
Wastewater
Removal,
pp.
5-1-5-21.
John
Wiley,
New
York
(1966).
4.
Babbitt,
H.
E.,
J. J.
Doland,
and J. L.
Cleasby.
Water
Supply
Engineering,
6th ed.
McGraw-Hill,
New
York
(1967).
5.
Peavy,
H.
S.,
D. R.
Rowe,
and G.
Tchobanoglous.
Environmental Engineering. McGraw-Hill,
New
York
(1985).
6.
Sanks,
R.
L.,
C. W.
Reh,
and A.
Amirtharajah
(Eds.),
Conference
Proceedings, Pumping Station
Design
for the
Practicing Engineer, Vol.
HI,
pp.
1173-1214
and
1247-
1256.
Department
of
Civil
Engineering
and
Engineering
Mechanics,
Montana
State
University, Bozeman,
MT
(1981).
Available
(1) as
photocopies
or (2) as
Vol.
HI
on
interlibrary
loan
from
the
university
library.
7.
Sanks,
R. L.
Water
Treatment Plant Design
for the
Practicing Engineer.
Ann
Arbor
Science
Publishers,
Ann
Arbor,
MI
(1978).
8.
Walton,
W. C.
Groundwater
Pumping Tests, Design
&
Analysis.
Lewis
Publishers,
Chelsea,
MI
(1987).
18-8. Suggested Reading
1.
Walski,
T. M.
Analysis
of
Water
Distribution Systems.
Van
Nostrand
Reinhold,
New
York,
NY
(1984).
or
4800
L
(1244
gal)—equivalent
to 35 min
reserve capacity
at
average daily
flowrate.
This
additional investment
in
tank size would probably avoid
an
occasional
depressurization
of the
system
and
time-consuming
repressurization.
System
layout.
A
sample layout
of the
required facilities
is
illustrated
in
Figures
18-27
and
18-28.

The
purpose
of
this chapter
is to
introduce
the key
issues involved
in the
design
of
sludge pumping sys-
tems.
A
number
of
significant
problems,
not
usually
met
in the
design
of
other pumping systems,
are
encountered
in
pumping sludge. These problems
include:
•
Variability
in the
nature
of the
pumped material
•
Resulting variability
in the
frictional
headless
char-
acteristics
•
Sludge behavior
(as a
non-Newtonian
fluid)
that
makes
traditional design (such
as
that
for
water
pumping)
inappropriate
• The
need
to
understand complex
fluid
mechanics
and
not
rely
on
"rule-of
-thumb"
approaches.
Due
to the
unusual
and
complex
fluid
mechanics asso-
ciated with
the
wide varieties
of
sludges, designers
are
cautioned
(1)
to
treat each sludge pumping application
as
a
unique design problem
and (2) to
develop site-
specific
design criteria based
on
detailed evaluation
of
the
specific
sludge characteristics.
The
discussion
in
this
chapter
is
limited
to
such problems
of
sludge sys-
tems
as the
selection
of
pumps, pipe, valves,
and
cleaning
and flushing
stations. Problems
associated
Chapter
1
9
System
Design
for
Sludge
Pumping
CARL
N.
ANDERSON
DAVIDJ.
HANNA
CONTRIBUTORS
Robert
H.
Brotherton
George
R.
Brower
Geoffrey
A.
Carthew
Michael
C.
Mulbarger
Wyett
C.
Playford
with
scum, screenings, grit, ash,
and
chemical
slurry
pumping
are not
addressed,
but
note that these materi-
als
behave,
in
general, entirely
differently
from
waste-
water
sludges.
The key to
pumping sludge
is to use (1) a
pump
properly sized
to
develop
sufficient
head
and (2) a
smooth pipe sized
to
produce
the
proper velocity (nei-
ther
too
high
nor too
low) without constrictions
or
projections
and
with
as few
bends
as
possible.
The key
to
maintaining such
a
system
is to
have large, easily
opened cleanouts
on the
pump,
at any
elbows
on the
suction side
of the
pump,
and
(where possible)
at all
elbows
on the
discharge side
of the
pump. Quick-dis-
connect
air
and/or water hose connections
on
both
the
suction
and
discharge sides
of the
pump
are
desirable
where
possible.
Sludge
lines
should rarely
be
smaller
than
150 mm (6
in.)
and
should preferably
be
larger.
Glass-lined pipe
is
superior where high concentrations
and
large amounts
of
grease
are
present. Glass lining
is
expensive, however, whereas cement-mortar lin-
ing
—
which
is
also
satisfactory
—
is
not.
The
elimina-
tion
of
elbows
and
constrictions
is of
more practical
importance than extreme smoothness
for
reducing
friction.

The
procedures presented
in
this chapter
are
appli-
cable only
to
short pipelines. Long pipelines
[1.6
km
(1 mi) or
longer] present
a
host
of
complex problems,
briefly
stated
in
Section
19-5.
In
general, extensive
field
testing
and a
thorough understanding
of the
liter-
ature
and
past
experience
with sludge pumping
to
develop engineering judgment
is
required
for the
suc-
cessful
design
of
systems
for
transporting sludge over
long
distances.
1
9-1
.
Hydraulic
Design
Some
of the
traditional, well-known
difficulties
in
evaluating
the
hydraulics
of
sludge
flow [1] are as
fol-
lows:
•
Sludge
is
nonhomogeneous
and has
variable, pecu-
liar
properties.
•
Parameters
useful
for
water
(such
as
Reynolds num-
ber)
do not
directly apply
to
sludge, which
is a
non-
Newtonian
fluid
that
may or may not
behave
as a
Bingham
plastic. Consequently, viscosity cannot
be
treated
as a
constant
in
pressure-drop calculations,
and
special
methods must
be
used
to
calculate
the
friction
loss.
•
Friction losses decrease
with
decreasing solids
con-
centration,
a
lower proportion
of
volatile solids,
and
increasing temperature.
The
suspended solids
con-
centration
is
generally accepted
as the
most domi-
nant
variable.
• Due to the
nature
of
biological
solids,
fresh
undi-
gested
sludges
and
sludges
from
combined sewage
behave more erratically than digested sludges.
•
Sludge
flow can be
either laminar
or
turbulent. Both
flow
regimes, shown
in
Figure
19-1,
are
widely used.
Flow
in
Pipelines
Sludges
are
most
efficiently
moved within
a
treatment
system
or
between locations
by
pumping through
pipelines.
The
unique
flow
characteristics
of
sludge
present unusual
difficulties
in
estimating
the
frictional
flow
characteristics,
and the
literature contains some
information
on
hydraulic design parameters
for
sev-
eral types
of
sludges,
the
bulk
of
which
is on
digested
and
raw
sludges
[3-8].
Before
1970,
designers typi-
cally relied
on
empirical rules
and
unreliable methods
for
predicting frictional headloss, although
the
funda-
mental theory
was
available
[4].
Better understanding
was
provided
by the
literature
of the
1970s
[9-12],
and
still more valuable knowledge
has
been gained
from
later studies
[2,
13-18].
A
brief, noncomprehen-
sive
summary
of fluid
mechanics applicable
to
sludge
systems
is
presented below.
Headloss
in
Laminar Flow
Sludges generally behave
as
non-Newtonian
fluids.
Because frictional headloss depends
on the fluid
rhe-
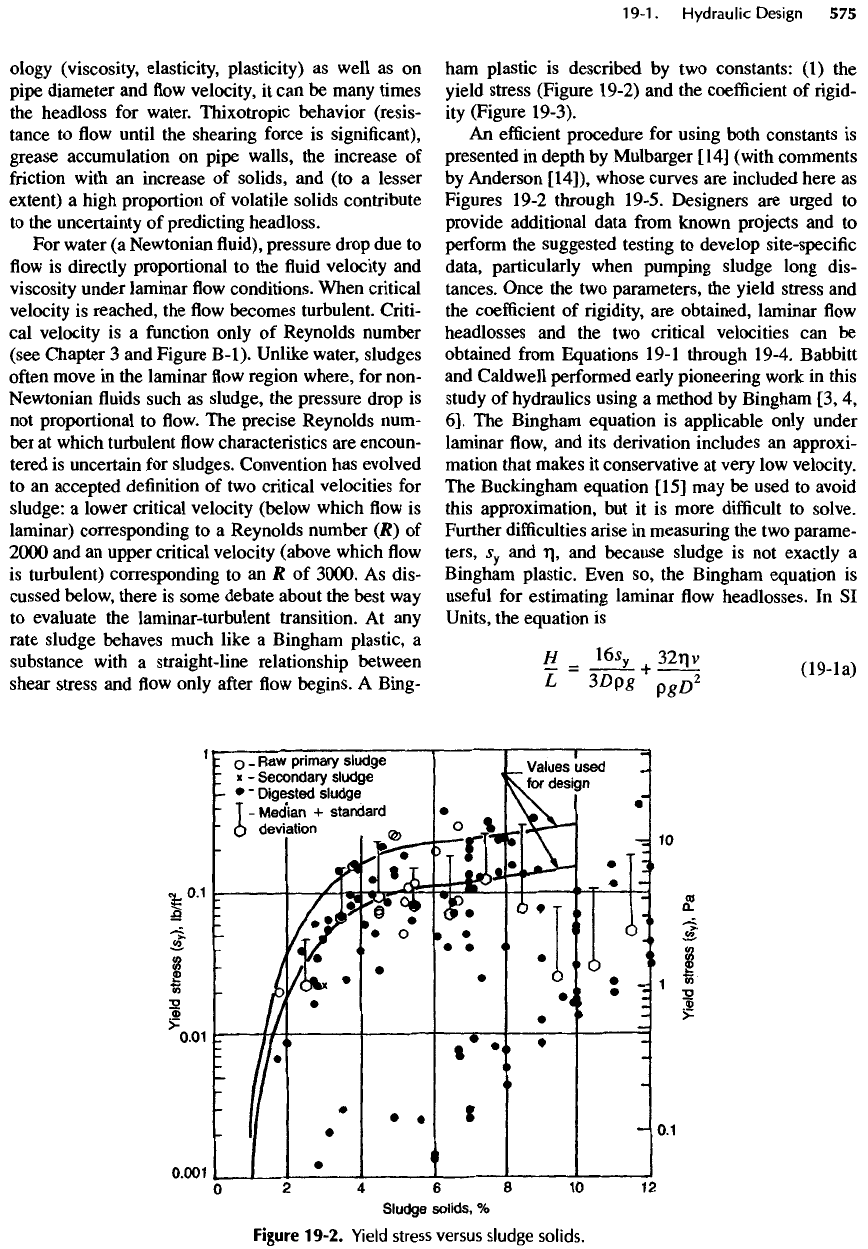
Figure
19-1.
Comparison
of
wastewater sludge
and
water
flowing
in
pipes.
After
EPA
[2].
ology
(viscosity, elasticity, plasticity)
as
well
as on
pipe
diameter
and flow
velocity,
it can be
many times
the
headloss
for
water.
Thixotropic
behavior (resis-
tance
to flow
until
the
shearing
force
is
significant),
grease accumulation
on
pipe walls,
the
increase
of
friction
with
an
increase
of
solids,
and (to a
lesser
extent)
a
high proportion
of
volatile
solids
contribute
to
the
uncertainty
of
predicting headloss.
For
water
(a
Newtonian
fluid),
pressure drop
due to
flow is
directly proportional
to the fluid
velocity
and
viscosity under laminar
flow
conditions. When critical
velocity
is
reached,
the flow
becomes turbulent. Criti-
cal
velocity
is a
function
only
of
Reynolds number
(see Chapter
3 and
Figure
B-I).
Unlike water, sludges
often
move
in the
laminar
flow
region where,
for
non-
Newtonian
fluids
such
as
sludge,
the
pressure drop
is
not
proportional
to flow. The
precise Reynolds num-
ber at
which turbulent
flow
characteristics
are
encoun-
tered
is
uncertain
for
sludges. Convention
has
evolved
to
an
accepted
definition
of two
critical velocities
for
sludge:
a
lower critical velocity (below which
flow is
laminar)
corresponding
to a
Reynolds number
(R
)
of
2000
and an
upper critical velocity (above which
flow
is
turbulent) corresponding
to an R of
3000.
As
dis-
cussed below, there
is
some debate about
the
best
way
to
evaluate
the
laminar-turbulent transition.
At any
rate sludge behaves much like
a
Bingham plastic,
a
substance
with
a
straight-line relationship between
shear
stress
and flow
only
after
flow
begins.
A
Bing-
ham
plastic
is
described
by two
constants:
(1) the
yield stress (Figure 19-2)
and the
coefficient
of rigid-
ity
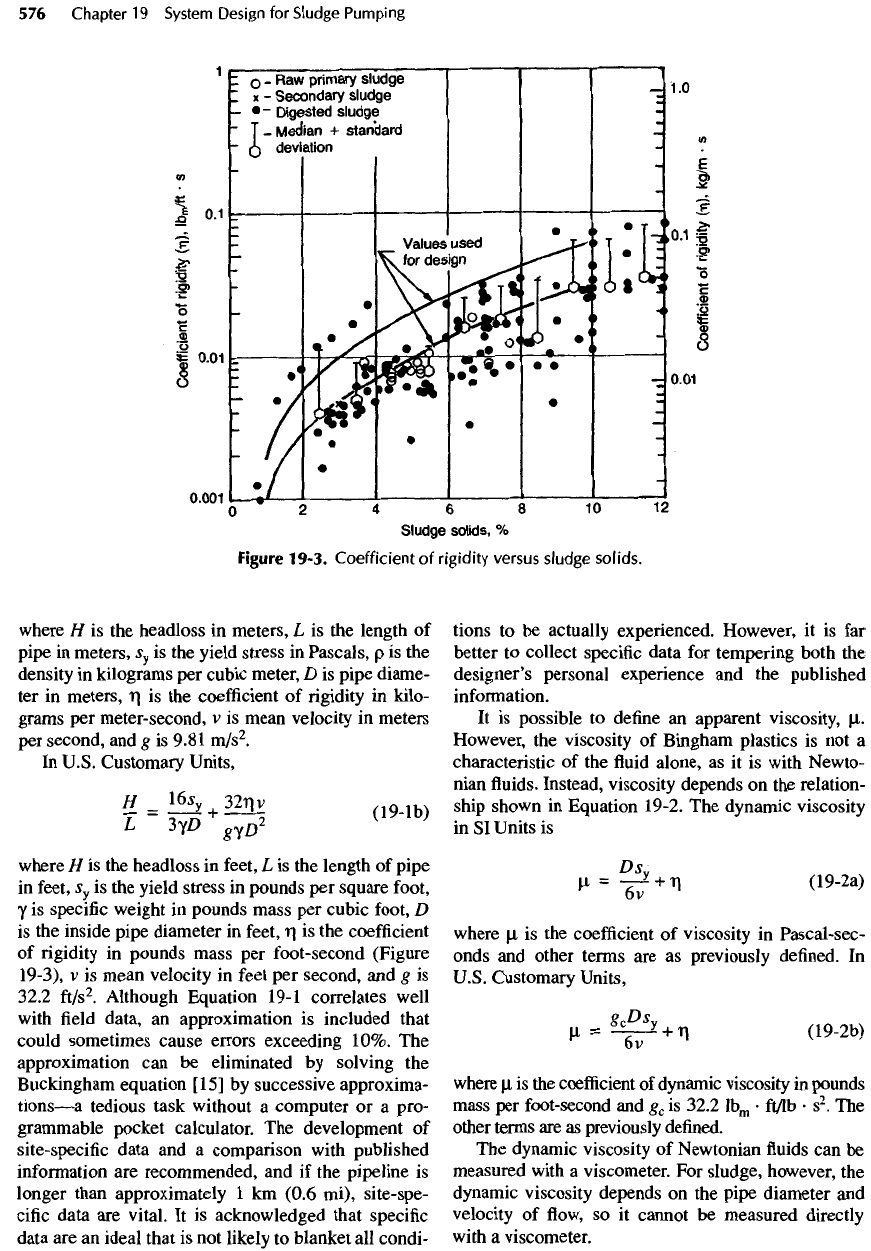
(Figure 19-3).
An
efficient
procedure
for
using both constants
is
presented
in
depth
by
Mulbarger [14] (with comments
by
Anderson
[14]),
whose curves
are
included here
as
Figures 19-2 through 19-5. Designers
are
urged
to
provide additional data
from
known projects
and to
perform
the
suggested testing
to
develop site-specific
data,
particularly when pumping sludge long dis-
tances. Once
the two
parameters,
the
yield stress
and
the
coefficient
of rigidity, are
obtained, laminar
flow
headlosses
and the two
critical velocities
can be
obtained
from
Equations 19-1 through 19-4. Babbitt
and
Caldwell performed early pioneering work
in
this
study
of
hydraulics using
a
method
by
Bingham
[3,
4,
6].
The
Bingham equation
is
applicable only under
laminar
flow, and its
derivation includes
an
approxi-
mation
that makes
it
conservative
at
very
low
velocity.
The
Buckingham equation
[15]
may be
used
to
avoid
this
approximation,
but it is
more
difficult
to
solve.
Further
difficulties
arise
in
measuring
the two
parame-
ters,
s
y
and
T|,
and
because sludge
is not
exactly
a
Bingham
plastic. Even
so, the
Bingham equation
is
useful
for
estimating laminar
flow
headlosses.
In SI
Units,
the
equation
is
I
=
Wo
+
32
^
2
<
19
-
la
>
L
3Dpg
p£
D
2
Figure
19-2.
Yield
stress
versus
sludge
solids.
where
H is the
headless
in
meters,
L is the
length
of
pipe
in
meters,
s
y
is the
yield stress
in
Pascals,
p is the
density
in
kilograms
per
cubic meter,
D is
pipe diame-
ter in
meters,
r|
is the
coefficient
of
rigidity
in
kilo-
grams
per
meter-second,
v is
mean velocity
in
meters
per
second,
and g is
9.81
m/s
2
.
In
U.S. Customary Units,
H
=
16
^y
+
32T
1
V
L
SyD
+
gyD
2
(iyib)
where
H is the
headloss
in
feet,
L is the
length
of
pipe
in
feet,
s
y
is the
yield stress
in
pounds
per
square foot,
Y
is
specific weight
in
pounds mass
per
cubic foot,
D
is the
inside pipe diameter
in
feet,
T)
is the
coefficient
of
rigidity
in
pounds mass
per
foot-second (Figure
19-3),
v is
mean velocity
in
feet
per
second,
and g is
32.2
ft/s
2
.
Although Equation 19-1 correlates well
with
field
data,
an
approximation
is
included that
could sometimes cause
errors
exceeding
10%.
The
approximation
can be
eliminated
by
solving
the
Buckingham
equation [15]
by
successive approxima-
tions
—
a
tedious task without
a
computer
or a
pro-
grammable pocket calculator.
The
development
of
site-specific
data
and a
comparison with published
information
are
recommended,
and if the
pipeline
is
longer than approximately
1 km
(0.6 mi), site-spe-
cific
data
are
vital.
It is
acknowledged that specific
data
are an
ideal
that
is not
likely
to
blanket
all
condi-
tions
to be
actually experienced. However,
it is far
better
to
collect
specific data
for
tempering both
the
designer's
personal experience
and the
published
information.
It is
possible
to
define
an
apparent viscosity,
ji.
However,
the
viscosity
of
Bingham
plastics
is not a
characteristic
of the fluid
alone,
as it is
with Newto-
nian
fluids.
Instead, viscosity depends
on the
relation-
ship shown
in
Equation 19-2.
The
dynamic viscosity
in
SI
Units
is
Ds
y
V
=
-g^
+
Tl
(19-2a)
where
^i
is the
coefficient
of
viscosity
in
Pascal-sec-
onds
and
other terms
are as
previously
defined.
In
U.S. Customary Units,
g
c
DSv
M-
=
-^T
+
7
I
(
19
'
2b
)
where
Ji
is the
coefficient
of
dynamic viscosity
in
pounds
mass
per
foot-second
and
g
c
is
32.2
lb
m
•
ftyib
.
s
2
.
The
other
terms
are as
previously
defined.
The
dynamic viscosity
of
Newtonian
fluids can be
measured with
a
viscometer.
For
sludge, however,
the
dynamic viscosity depends
on the
pipe diameter
and
velocity
of flow, so it
cannot
be
measured directly
with
a
viscometer.
Figure
19-3.
Coefficient
of
rigidity
versus
sludge
solids.
