Principles of Finance with Excel (Основы финансов c Excel)

Подождите немного. Документ загружается.

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 18

Varying the portfolio composition—graphing all possible portfolios

Suppose we vary the composition of the portfolio, letting the percentage of GM vary

from 0% to 100%. In cells G19:H29 below we generate a table of portfolio returns E(r

) and

standard deviations

ABC DEFGHI

GM MSFT

Average 14.25% 62.72%

Variance 6.38% 14.43%

Sigma 25.25% 37.99%

Covariance of returns -5.52% <-- =COVAR(B9:B18,C9:C18)

Portfolio return and risk

Percentage in GM 50%

Percentage in MSFT 50%

Expected portfolio return 38.49% <-- =B9*B3+B10*C3

Portfolio variance 2.44% <-- =B9^2*B4+B10^2*C4+2*B9*B10*B6

Portfolio standard deviation 15.62% <-- =SQRT(B13)

Percentage

in GM Sigma

Expected

return

0.0 37.99% 62.72%

0.1 32.80% 57.87%

0.2 27.79% 53.03%

0.3 23.08% 48.18%

0.4 18.88% 43.33%

0.5 15.62% 38.49%

0.6 13.98% 33.64%

0.7 14.51% 28.79%

0.8 17.01% 23.95%

0.9 20.78% 19.10%

1.0 25.25% 14.25%

PORTFOLIO STATISTICS

FOR A GM-MSFT PORTFOLIO

Portfolio Returns: Expected Return

and Standard Deviation

10%

20%

30%

40%

50%

60%

70%

12% 17% 22% 27% 32% 37% 42%

Standard deviation of return

Expected return E(r

)

=SQRT(F18^2*$B$3+(1-F18)^2*$C$3

+2*F18*(1-F18)*$B$5)

=F18*$B$2+(1-F18)*$C$2

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 19

An Excel Note: Using Data Table to simplify the calculations

The table in cells G18:H28 above were generated using formulas for the standard

deviation and expected return. Each cell contains a formula (note the use of absolute and relative

cell references in these formulas). You can simplify the building of the table by using the Data

table technique discussed in Chapter 30. Data table is not an easy technique to master, but it

makes building tables much easier. Here’s an example:

ABC DEFGHI

GM MSFT

Average 14.25% 62.72%

Variance 6.38% 14.43%

Sigma 25.25% 37.99%

Covariance of returns -5.52% <-- =COVAR(B9:B18,C9:C18)

Portfolio return and risk

Percentage in GM 50%

Percentage in MSFT 50%

Expected portfolio return 38.49% <-- =B9*B3+B10*C3

Portfolio variance 2.44% <-- =B9^2*B4+B10^2*C4+2*B9*B10*B6

Portfolio standard deviation 15.62% <-- =SQRT(B13)

Percentage

in GM Sigma

Expected

return

15.62% 38.49%

0% 37.99% 62.72%

10% 32.80% 57.87%

20% 27.79% 53.03%

30% 23.08% 48.18%

40% 18.88% 43.33%

50% 15.62% 38.49%

60% 13.98% 33.64%

70% 14.51% 28.79%

80% 17.01% 23.95%

90% 20.78% 19.10%

100% 25.25% 14.25%

PORTFOLIO STATISTICS FOR A GM-MSFT PORTFOLIO

using Data Table

Portfolio Returns: Expected Return

and Standard Deviation

10%

20%

30%

40%

50%

60%

70%

12% 17% 22% 27% 32% 37% 42%

Standard deviation of return σ

Expected return E(r

)

Contains

formula "=B14"

Contains

formula "=B12"

You create the data table by marking the cells G17:H29. The command Data|Table

brings up the dialog box to which you add the appropriate cell reference:

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 20

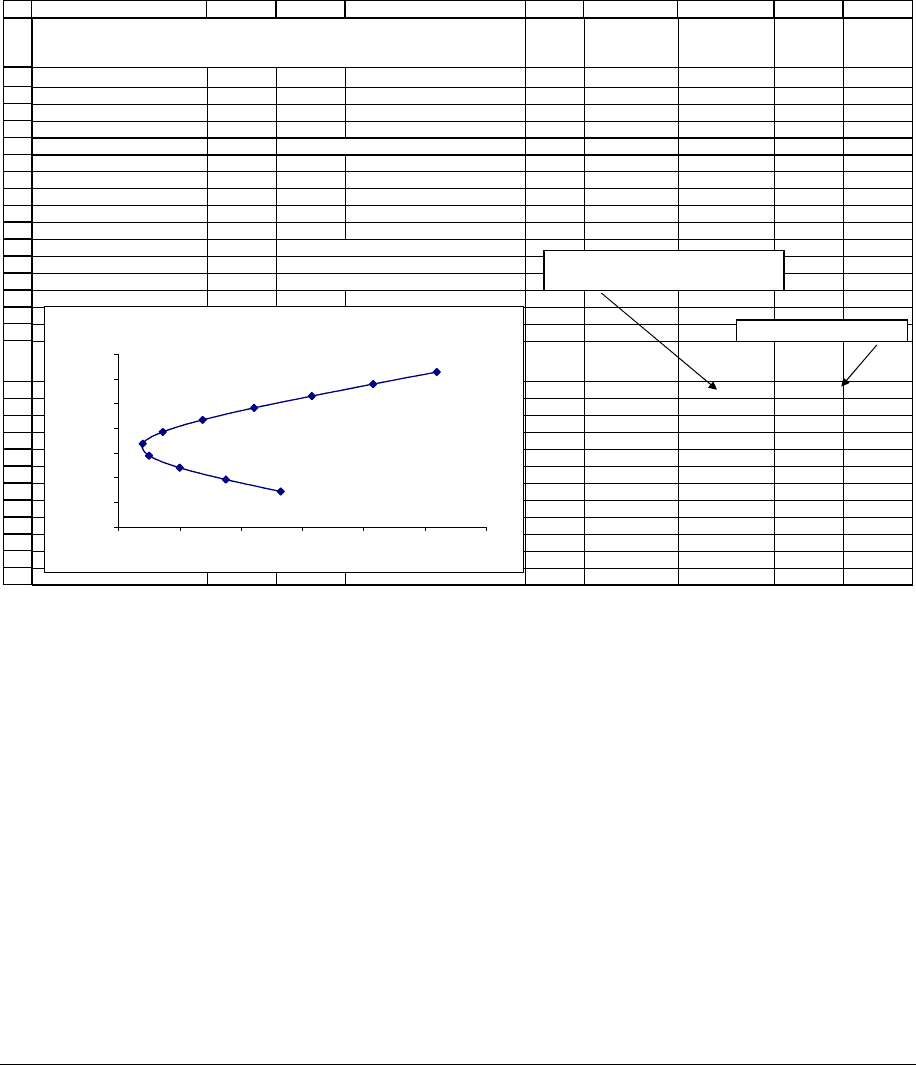
Better portfolios ... worse portfolios ...

Take a careful look at the graph in the above spreadsheet—it shows the standard

deviation

of the portfolio returns on the x-axis and the corresponding expected portfolio return

E(r

) on the y-axis. Looking at the graph it is easy to see that some portfolios are better than

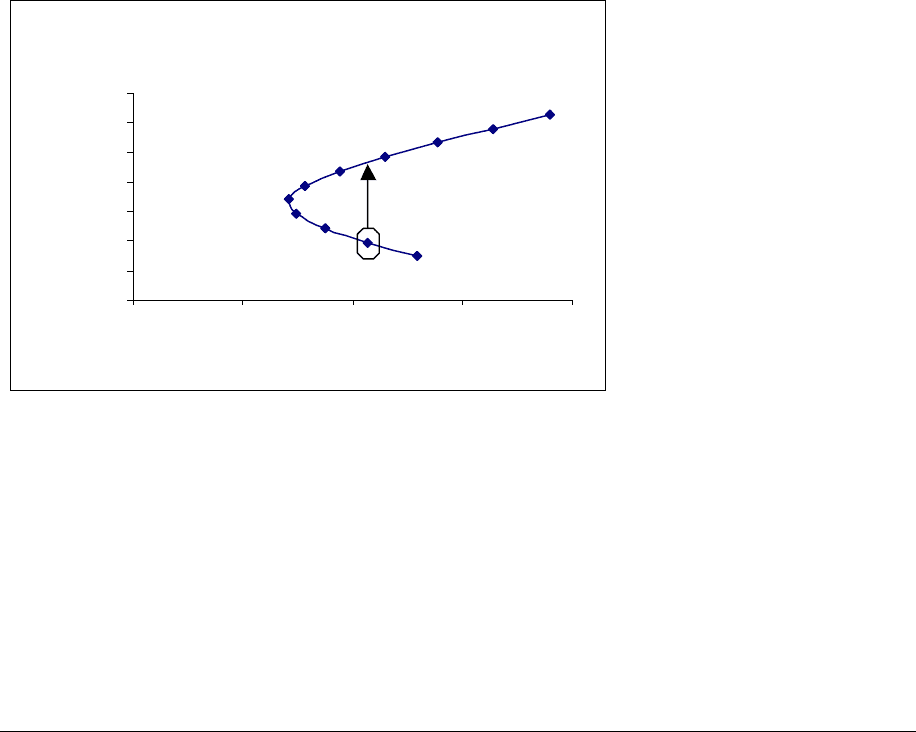
others. Consider, for example, the portfolio invested 90% in GM and 10% in MSFT (this

portfolio is circled in the graph below). By investing in the portfolio indicated by the arrow, you

can improve the expected return without increasing the riskiness of the return. Thus the circled

portfolio is not optimal. In fact none of the portfolios on the bottom part of the graph are

optimal: Each is dominated by a portfolio on the top part of the graph which has the same

standard deviation

and higher expected return E(r

Expected Return and Standard Deviation of

Portfolio Return

10%

20%

30%

40%

50%

60%

70%

0% 10% 20% 30% 40%

Standard deviation of portfolio return,

Expected portfolio return,

E(r

)

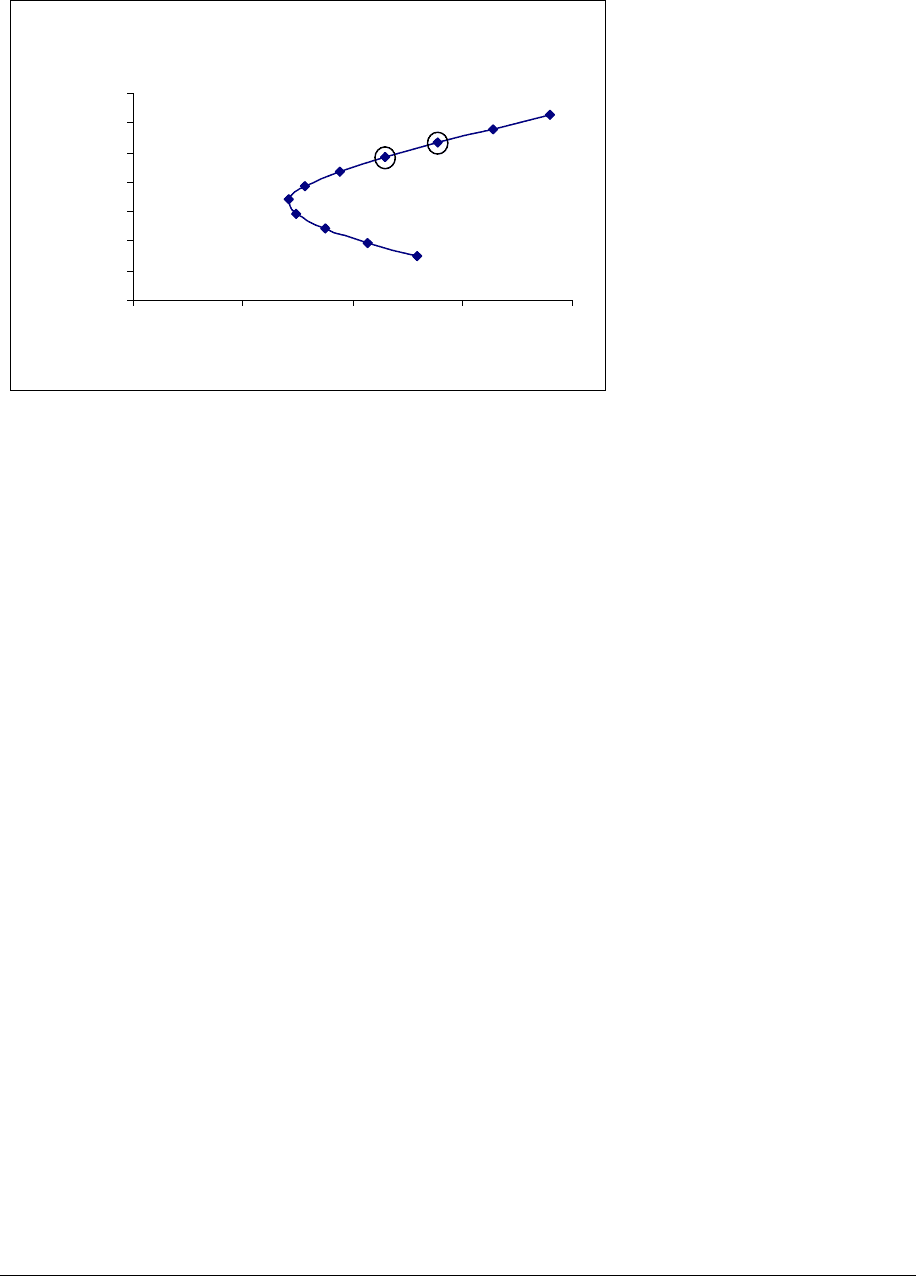
On the other hand, consider the two portfolios circled below:

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 21

Expected Return and Standard Deviation of

Portfolio Return

10%

20%

30%

40%

50%

60%

70%

0% 10% 20% 30% 40%

Standard deviation of portfolio return,

Expected portfolio return,

E(r

)

There is a clear risk-return tradeoff between these two portfolios—it is impossible to say that one

is unequivocally better than the other. The portfolio with the higher return also has the higher

standard deviation of returns. All of the portfolios on the top part of the graph have this

property. This top part of the graph is called the efficient frontier. The efficient frontier is the

area of hard portfolio choices—along the efficient frontier, portfolios with greater expected

return require you to undertake greater risk.

The efficient frontier slopes upward from left to right. What this means is that the choice

between any two portfolios on the efficient frontier involves a tradeoff between higher expected

portfolio return, E(r

), and higher risk as indicated by a higher standard deviation of the return,

. An investor choosing only risky portfolios would choose a portfolio on the efficient frontier.

In the next section we investigate some of the properties of the efficient frontier.

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 22

12.4. The efficient frontier and the minimum variance portfolio

The efficient frontier is the set of all portfolios which are on the upward-sloping part of

the graph above. “Upward-sloping” means that portfolios on the efficient frontier involve

difficult choices—increasing expected portfolio return E(r

) has the cost of increasing portfolio

standard deviation

. If you are choosing investment portfolios that are a mix of GM and

MSFT stock, then clearly the only portfolios you would be interested in are those on the efficient

frontier. These portfolios are the only ones which have a “northeast” risk-return relation.

In order to calculate the efficient frontier, we have to find its starting point, the portfolio

with the minimum standard deviation of returns. In the jargon of finance, this portfolio is

(somewhat confusingly) called the minimum-variance portfolio; just recall that if the portfolio

has minimum variance it also has minimum standard deviation. The minimum variance portfolio

is the portfolio on the right-hand corner of the efficient frontier; the graph below indicates its

approximate location:

Expected Return and Standard Deviation of Portfolio Return

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40

Standard deviation of portfolio return,

Expected portfolio return, E(r

)

The minimum variance

portfolio

The portfolios on the top are the

efficient frontier--

portfolios with a positive risk-

return tradeoff

We can find the minimum variance portfolio in two ways—either by using the

Solver or

by using a bit of mathematics. We illustrate both methods:

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 23

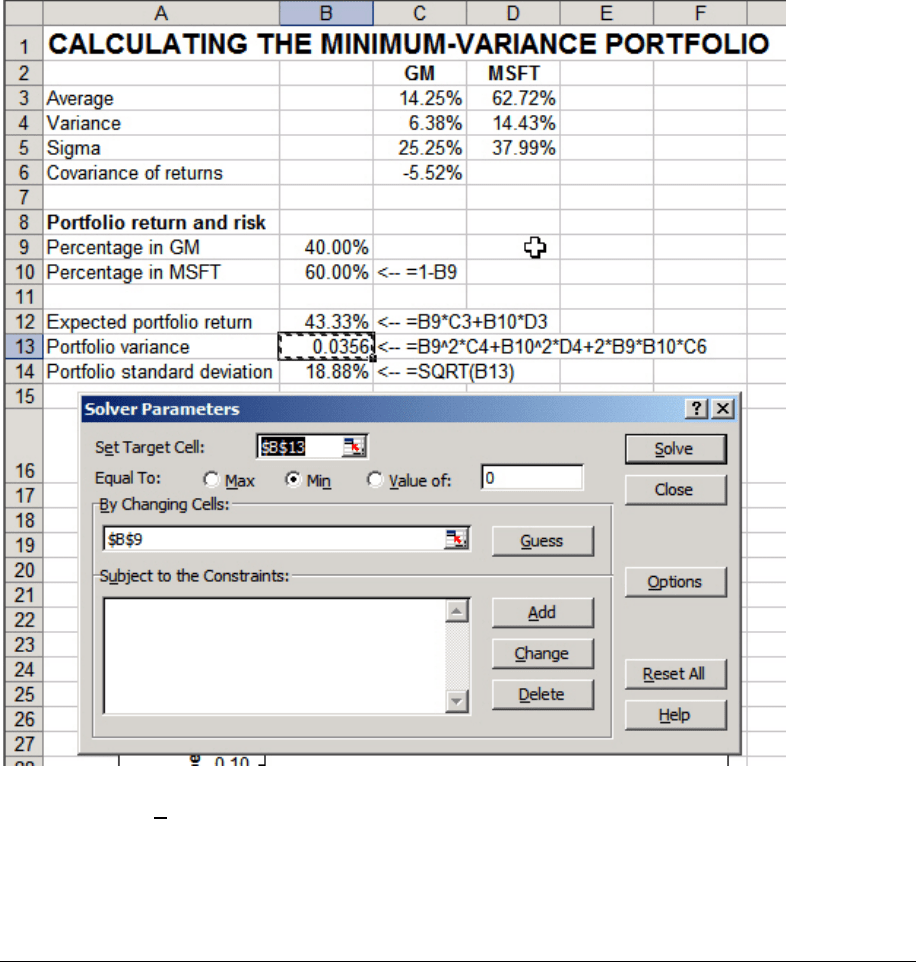
Using Excel’s Solver

By using the Solver (see Chapter 32), we can calculate the percentage of GM in a

portfolio which has minimum variance. The screen below shows the

Solver dialog box. In this

box, we’ve asked

Solver to minimize the portfolio variance (cell B13) by changing the

percentage of GM stock in the portfolio (cell B9):

Pushing

Solve gives:

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 24

ABCDEFG

CALCULATING THE MINIMUM-VARIANCE PORTFOLIO

GM MSFT

Average 14.25% 62.72%

Variance 6.38% 14.43%

Sigma 25.25% 37.99%

Covariance of returns -5.52%

Portfolio return and risk

Percentage in GM 62.64%

Percentage in MSFT 37.36% <-- =1-B9

Expected portfolio return 32.36% <-- =B9*C3+B10*D3

Portfolio variance 0.0193 <-- =B9^2*C4+B10^2*D4+2*B9*B10*C6

Portfolio standard deviation 13.90% <-- =SQRT(B13)

Thus the minimum variance portfolio has 62.64% in GM and 37.36% in MSFT.

Minimum variance portfolios using calculus

There’s actually a formula for the minimum variance portfolio:

() ( )

() ( ) ( )

MSFT GM MSFT

GM MSFT GM MSFT

Var r Cov r r

Var r Var r Cov r r

−

+−

Using this formula, which is derived in Appendix 1 (page000), is simpler than using

Solver. Implementing the formula in Excel gives the same answer as that given by Solver:

Although—as explained in Chapter 32—Solver and Goal Seek are in most cases interchangeable, this is a

calculation which

Solver does easily, but which cannot be done in Goal Seek.

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 25

ABCDEF

GM MSFT

Average 14.25% 62.72%

Variance 6.38% 14.43%

Sigma 25.25% 37.99%

Covariance of returns -5.52%

Minimum variance portfolio--analytic formula

Percentage in GM 62.64% <-- =(D4-C6)/(C4+D4-2*C6)

Percentage in MSFT 37.36% <-- =1-B9

Expected portfolio return 32.36% <-- =B9*C3+B10*D3

Portfolio variance 0.0193 <-- =B9^2*C4+B10^2*D4+2*B9*B10*C6

Portfolio standard deviation 13.90% <-- =SQRT(B13)

CALCULATING THE MINIMUM-VARIANCE PORTFOLIO

WITH A FORMULA

The efficient frontier and the minimum variance portfolio

Now that we know the minimum variance portfolio, we can plot the efficient frontier, the

set of all the portfolios with an economically-meaningful return-risk tradeoff. “Economically-

meaningful return-risk tradeoff” means that along the efficient frontier additional portfolio return

E(r

) is achieved at the cost of additional portfolio standard deviation

. The efficient frontier is

all portfolios that are to the right of the minimum variance portfolio.

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 26

ABCDEFGHIJK

GM MSFT

Average 14.25% 62.72%

Variance 6.38% 14.43%

Sigma 25.25% 37.99%

Covariance of returns -5.52%

Minimum variance portfolio--analytic formula

Percentage in GM 62.64% <-- =(D4-C6)/(C4+D4-2*C6)

Percentage in MSFT 37.36% <-- =1-B9

Expected portfolio return 32.36% <-- =B9*C3+B10*D3

Portfolio variance 0.0193 <-- =B9^2*C4+B10^2*D4+2*B9*B10*C6

Portfolio standard deviation 13.90% <-- =SQRT(B13)

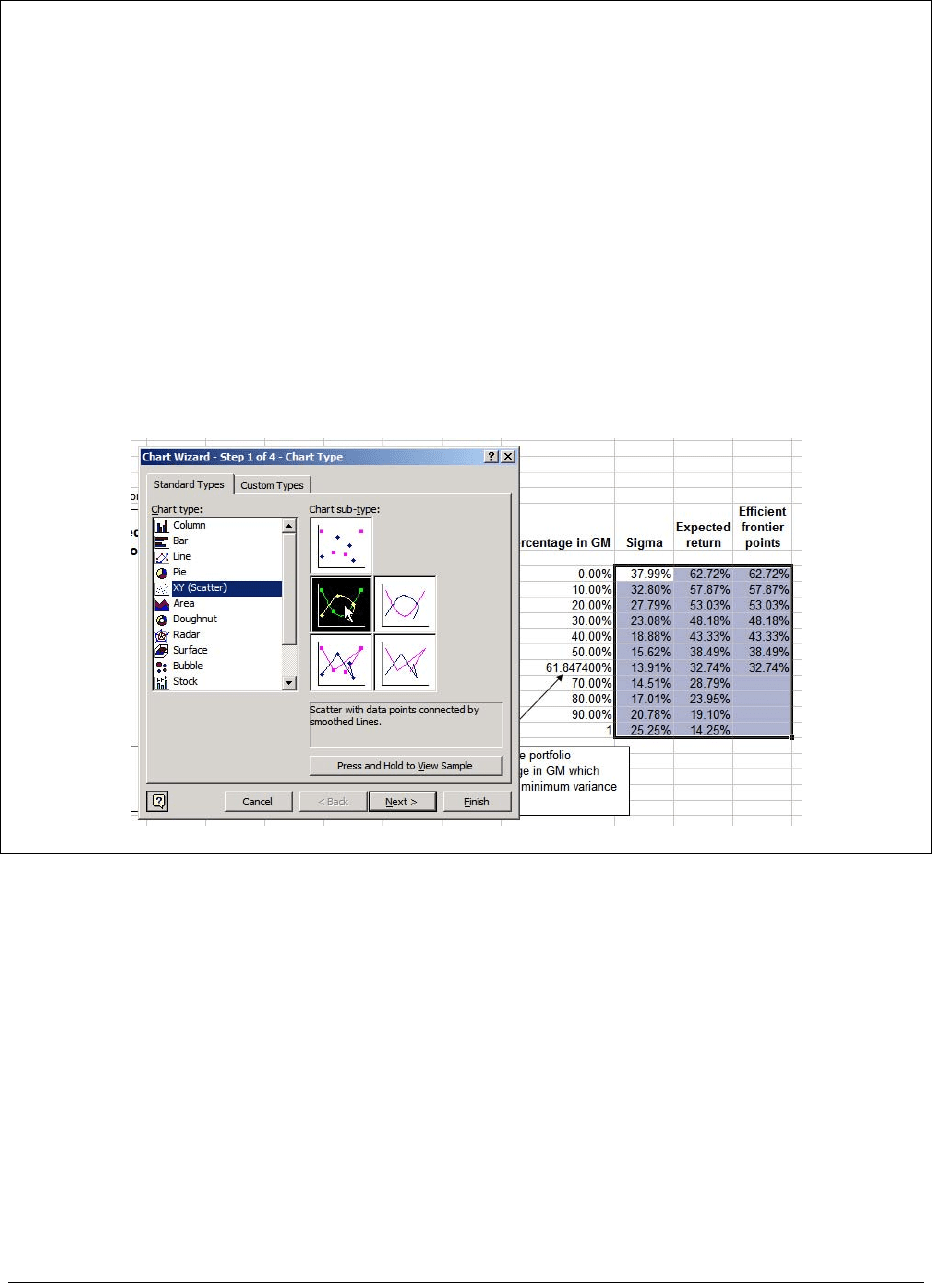
Percentage in GM Sigma

Expected

return

Efficient

frontier

points

0.00% 37.99% 62.72% 62.72%

10.00% 32.80% 57.87% 57.87%

20.00% 27.79% 53.03% 53.03%

30.00% 23.08% 48.18% 48.18%

40.00% 18.88% 43.33% 43.33%

50.00% 15.62% 38.49% 38.49%

61.847400% 13.91% 32.74% 32.74%

70.00% 14.51% 28.79%

80.00% 17.01% 23.95%

90.00% 20.78% 19.10%

1 25.25% 14.25%

CALCULATING THE MINIMUM-VARIANCE PORTFOLIO

WITH A FORMULA

Expected Return and Standard Deviation of

Portfolio Return--Showing Efficient Frontier

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

0.00 0.10 0.20 0.30 0.40

Standard deviation of portfolio return,

Expected portfolio return, E(r

)

This is the portfolio

percentage in GM which

gives the minimum variance

portfolio.

PFE Chapter 12, Appendix: The efficient frontier with more than two assets Page 27

Excel trick

The graph of the efficient frontier shown above is an XY Scatter plot. The x-data is the

data for sigma in I17:I27. Cells J17:J27 give the data for the portfolio expected returns, and cells

K17:K27 give data for the expected returns only for efficient portfolios. The two data series,

J17:J27 and K17:K27, constitute the y-data for the XY scatter plot. Where they coincide, Excel

superimposes them, creating the effect seen in the graph.

To create the graph, mark the three columns I17:K27. Then go to the chart wizard and

pick XY (Scatter) as shown below. Proceed from there to build the graph.

12.5. The effect of correlation on the efficient frontier

When we looked at the “coin-flip” economy of section 12.1, we concluded that the

correlation between asset returns made a big difference. In this section we examine the effect of

stock return correlation on portfolio returns, repeating the correlation experiment of section 12.1

for a more “real world” example.