Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

158 Chapter 2 The Heat Equation

and separate these equalities into two ordinary differential equations linked by

the common parameter λ



+λ

φ = 0, 0 < x < a, (4)



+λ

kT =0, 0 < t. (5)

The boundary conditions on u can be translated into conditions on φ,be-

cause they are homogeneous conditions. The boundary conditions in product

form are

∂u

∂x

(0, t) = φ



(0)T(t) = 0, 0 < t,

∂u

∂x

(a, t) = φ



(a)T(t) = 0, 0 < t.

To satisfy these equations, we must have the function T(t) always zero (which

would make u(x, t) ≡ 0), or else



(0) =0,φ



(a) =0.

The second alternative avoids the trivial solution.

We now have a homogeneous differential equation for φ together with ho-

mogeneous boundary conditions:



+λ

φ = 0, 0 < x < a, (6)



(0) = 0,φ



(a) =0. (7)

A problem of this kind is called an eigenvalue problem. We are looking for those

values of the parameter λ

for which nonzero solutions of Eqs. (6) and (7)

may exist. Those values are called eigenvalues, and the corresponding solutions

are called eigenfunctions. Note that the signiﬁcant parameter is λ

,notλ.The

square is used only for convenience. It is worth mentioning that we already

saw an eigenvalue problem in Section 3 and in the Euler buckling problem of

Chapter 0.

The general solution of the differential equation in Eq. (6) is

φ(x) = c

cos(λx) +c

sin(λx).

Applying the boundary condition at x = 0, we see that φ



(0) = c

λ = 0, giv-

ing c

= 0orλ = 0. We put aside the case λ = 0andassumec

= 0, so

φ(x) = c

cos(λx). Then the second boundary condition requires that φ



(a) =

−c

λ sin(λa) = 0. Once again, we may have c

= 0orsin(λa) = 0. But c

= 0

makes φ(x) ≡ 0. We choose therefore to make sin(λa) = 0byrestrictingλ to

2.4 Example: Insulated Bar 159

the values π/a, 2π/a, 3π/a,.... We label the eigenvalues with a subscript:



nπ



,φ

(x) = cos(λ

x), n = 1, 2,....

Notice that any constant multiple of an eigenfunction is still an eigenfunction;

thus, we may take c

=1 for simplicity.

Returning to the case λ = 0, we see that Eqs. (6) and (7) become



=0, 0 < x < a,



(0) =0,φ



(a) =0.

The solution of the differential equation is φ(x) = c

+ c

x . Both boundary

conditions say c

= 0. Therefore φ(x) is a (any) constant. Thus 0 is an eigen-

value of the problem Eqs. (6) and (7), and we designate

=0,φ

(x) = 1.

Let us summarize our ﬁndings by saying that the eigenvalue problem,

Eqs. (6) and (7), has the solution







=0,φ

(x) = 1,



nπ



,φ

(x) = cos(λ

x), n = 1, 2,....

Now that the numbers λ

are known, we can solve Eq. (5) for T(t),ﬁnding

(t) = 1, T

(t) = exp



−λ



The products φ

(x)T

(t) give solutions of the partial differential equation (1)

that satisfy the boundary conditions, Eq. (2):

(x, t) = 1, u

(x, t) = cos(λ

x) exp



−λ



. (8)

Because the partial differential equation and the boundary conditions are all

linear and homogeneous, the principle of superposition applies, and any linear

combination of solutions is also a solution. The solution u(x, t) of the whole

system may therefore have the form

u(x, t) = a

∞



cos(λ

x) exp



−λ



. (9)

There is only one condition of the original set remaining to be satisﬁed, the

initial condition Eq. (3). For u(x, t) in the form of Eq. (9), the initial condi-

tion is

u(x, 0) = a

∞



cos(λ

x) = f (x), 0 < x < a.

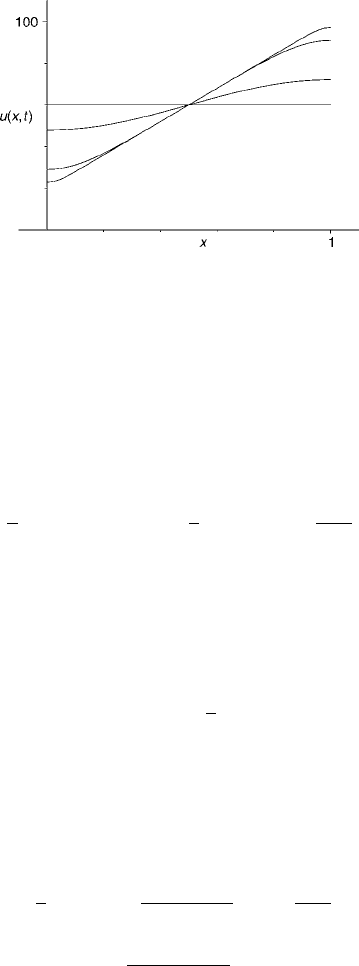
160 Chapter 2 The Heat Equation

Figure 4 The solution of the example, u(x, t), as a function of x for several times.

The initial temperature distribution is f (x) = T

+(T

−T

)x/a. For this illustra-

tion, T

= 20, T

= 100, and the times are chosen so that the dimensionless time

kt/a

takes the values 0.001, 0.01, 0.1, and 1. The last case is indistinguishable from

the steady state. See the CD also.

Because λ

= nπ/a, we recognize a problem in Fourier series and can imme-

diately cite formulas for the coefﬁcients:



f (x) dx, a



f (x ) cos



nπx



dx. (10)

When these coefﬁcients are computed and substituted in the formulas for

u(x, t), that function becomes the solution to the initial value–boundary value

problems, Eqs. (1)–(3). Notice that when t →∞, all other terms in the sum-

mation for u(x, t) disappear, leaving

lim

t→∞

u(x, t) = a



f (x ) dx.

Example.

Find the complete solution of Eqs. (1)–(3) for the initial temperature dis-

tribution f (x) = T

+ (T

− T

)x/a .Itrequiresnointegrationtoﬁndthat

=(T

)/2. The remaining coefﬁcients are





−T



cos



nπx



= 2(T

−T

)

cos(nπ)−1

Thus the solution is given by Eq. (9) with these coefﬁcients for a

and a

Agraphofu(x, t) as a function of x is shown in Fig. 4 and as an animation on

the CD.



2.4 Example: Insulated Bar 161

EXERCISES

1. Using the initial condition

u(x, 0) = T

, 0 < x < a,

ﬁnd the solution u(x, t) of Eqs. (1)–(3). Sketch u(x, 0), u(x, t) for some

t > 0 (using the ﬁrst three terms of the series), and the steady-state solu-

tion.

2. Repeat Exercise 1 using the initial condition

u(x, 0) = T





, 0 < x < a.

3. Same as Exercise 1, but with initial condition

u(x, 0) =











, 0 < x <

(a −x)

< x < a.

4. Solve Eqs. (1)–(3) using the initial condition u(x, 0) = f (x),where

f (x) =











, 0 < x <

< x < a.

5. Consider this heat problem, which is related to Eqs. (1)–(3):

∂

∂x

∂u

∂t

, 0 < x < a, 0 < t,

∂u

∂x

(0, t) = S

∂u

∂x

(a, t) = S

, 0 < t,

u(x, 0) = f (x), 0 < x < a.

a. Show that the steady-state problem has a solution if and only if S

and give a physical reason why this should be true. (Recall that the heat

ﬂux q is proportional to the derivative of u with respect to x.) Find the

steady-state solution if this condition is met.

b. Ifthesteady-statesolutionv(x) exists, show that the “transient,”

w(x, t) = u(x, t) − v(x), has the boundary conditions

∂w

∂x

(0, t) = 0,

∂w

∂x

(a, t) = 0, 0 < t.

162 Chapter 2 The Heat Equation

Show that the function u(x , t) = A(kt + x

/2) + Bx satisﬁes the heat

equation for arbitrary A and B and that A and B can be chosen to satisfy

the boundary conditions

∂u

∂x

(0, t) = S

∂u

∂x

(a, t) = S

, 0 < t.

What happens to u(x, t) as t increases if S

=S

6. Ve r i f y t h a t u

(x, t) in Eq. (8) satisﬁes the partial differential equation (1)

and the boundary conditions, Eq. (2).

7. State the eigenvalue problem associated with the solution of the heat prob-

lem in Section 3. Also state its solution.

8. Suppose that the function φ(x) satisﬁes the relation



(x)

φ(x)

> 0.

Show that the boundary conditions φ



(0) = 0, φ



(a) = 0, then force φ(x)

to be identically 0. Thus, a positive “separation constant” can only lead to

the trivial solution.

9. Refer to Eqs. (9) and (10), which give the solution of the problem stated

in Eqs. (1)–(3). If f is sectionally continuous, the coefﬁcients a

→ 0as

n →∞.Fort =t

> 0, ﬁxed, the solution is

u(x, t

) =a

∞



exp



−λ



cos(λ

and the coefﬁcients of this cosine series are

) =a

exp



−λ



Show that A

) → 0 so rapidly as n →∞that the series given in the

preceding converges uniformly 0 ≤x ≤ a. (See Chapter 1, Section 4, The-

orem 1.) Show the same for the series that represents

∂

∂x

(x, t

10. Sketch the functions φ

, φ

,andφ

and verify graphically that they satisfy

the boundary conditions of Eq. (7).

11. The boundary conditions Eq. (2) require that

∂u

∂x

(0, t) = 0, 0 < t,

and similarly at x = a.Doesthismeanthatu is constant at x = 0?

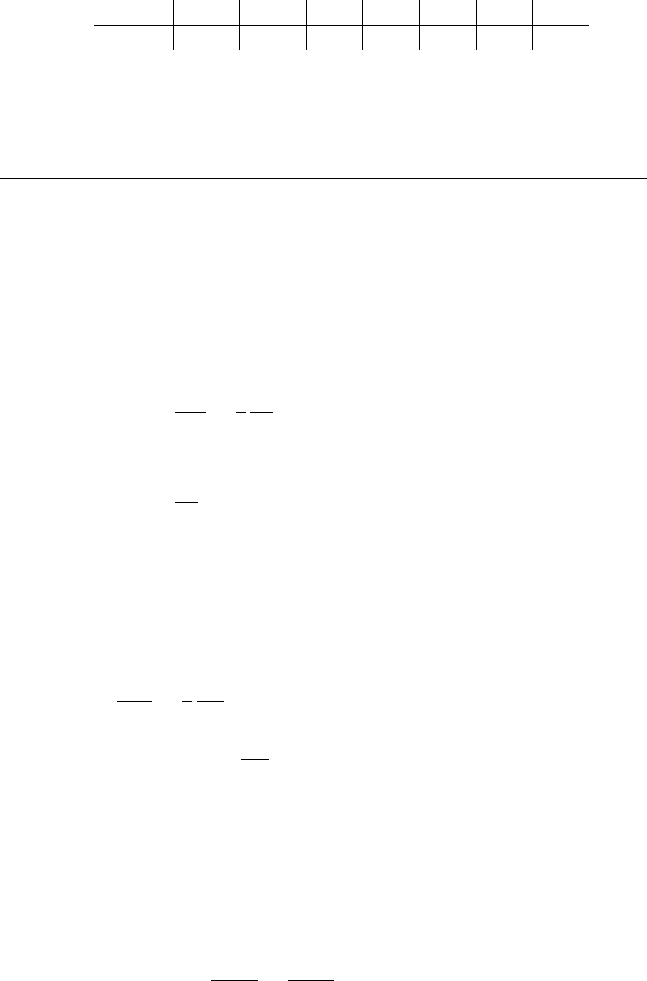
2.5 Example: Different Boundary Conditions 163

12. This table gives values of u(0, t) for the function u found in the example

and shown in Fig. 4. Make a graph of u(0, t) and describe the graph in

words.

kt/a

: 0.001 0.003 0.01 0.03 0.1 0.3 1

u(0, t): 22.9 24.9 29.0 35.6 47.9 58.3 60.0

13. Check that the partial differential equation and boundary conditions are

satisﬁed by the series in Eq. (9).

2.5 Example: Different Boundary Conditions

In many important cases, boundary conditions at the two endpoints will be

different kinds. In this section we shall solve the problem of ﬁnding the tem-

perature in a rod having one end insulated and the other held at a constant

temperature. The boundary value–initial value problem satisﬁed by the tem-

perature in the rod is

∂

∂x

∂u

∂t

, 0 < x < a, 0 < t, (1)

u(0, t) = T

, 0 < t, (2)

∂u

∂x

(a, t) = 0, 0 < t, (3)

u(x, 0) = f (x), 0 < x < a. (4)

It is easy to verify that the steady-state solution of this problem is v(x) = T

Using this information, we can ﬁnd the boundary value–initial value problem

satisﬁed by the transient temperature w(x, t) = u(x, t) − T

∂

∂x

∂w

∂t

, 0 < x < a, 0 < t, (5)

w(0, t) = 0,

∂w

∂x

(a, t) = 0, 0 < t, (6)

w(x, 0) = f (x) −T

=g(x), 0 < x < a. (7)

Since this problem is homogeneous, we can attack it by the method of sep-

aration of variables. The assumption that w(x, t) has the form of a product,

w(x, t) = φ(x)T(t), and insertion of w in that form into the partial differential

equation (5) lead, as before, to



(x)

φ(x)



(t)

kT(t)

=constant. (8)

164 Chapter 2 The Heat Equation

The boundary conditions take the form

φ(0)T(t) = 0, 0 < t, (9)



(a)T(t) = 0, 0 < t. (10)

As before, we conclude that φ(0) and φ



(a) should both be zero:

φ(0) = 0,φ



(a) =0. (11)

By trial and error we ﬁnd that a positive or zero separation constant in Eq. (8)

forces φ(x) ≡ 0. Thus we take the constant to be −λ

. The separated equations

are



+λ

φ = 0, 0 < x < a, (12)



+λ

kT =0, 0 < t. (13)

Now, the general solution of the differential equation (12) is

φ(x) = c

cos(λx) +c

sin(λx).

The boundary condition, φ(0) = 0, requires that c

=0, leaving

φ(x) = c

sin(λx).

The boundary condition at x =a now takes the form



(a) =c

λ cos(λa) = 0.

The three choices are: c

= 0, which gives the trivial solution; λ = 0, which

should be investigated separately (Exercise 2), and cos(λa) = 0. The third al-

ternative — the only acceptable one — requires that λa be an odd multiple of

π/2, which we may express as

(2n −1)π

, n =1, 2,.... (14)

Thus, we have found that the eigenvalue problem consisting of Eqs. (11)

and (12) has the solution

(2n −1)π

,φ

(x) = sin(λ

x), n = 1, 2, 3,.... (15)

With the eigenfunctions and eigenvalues now in hand, we return to the dif-

ferential equation (13), whose solution is

(t) = exp



−λ



2.5 Example: Different Boundary Conditions 165

As in previous cases, we assemble the general solution of the homogeneous

problem expressed in Eqs. (5)–(7) by forming a general linear combination of

our product solutions,

w(x, t) =

∞



n=1

sin(λ

x) exp



−λ



. (16)

Thechoiceofthecoefﬁcients,b

,mustbemadesoastosatisfytheinitialcon-

dition, Eq. (8). Using the form of w given by Eq. (16), we ﬁnd that the initial

condition is

w(x, 0) =

∞



n=1

sin



(2n −1)π x



=g(x), 0 < x < a. (17)

A routine Fourier sine series for the interval 0 < x < a would involve the func-

tions sin(nπ x/a), rather than the functions we have. By one of several means

(Exercises 10–12), it may be shown that the series in Eq. (17) represents the

function g(x),providedthatg is sectionally smooth and that we choose the

coefﬁcients by the formula



g(x) sin



(2n −1)π x



dx. (18)

Now the original problem is completely solved. The solution is

u(x, t) = T

∞



n=1

sin(λ

x) exp



−λ



. (19)

It should be noted carefully that the T

term in Eq. (19) is the steady-state

solution in this case; it is not part of the separation-of-variables solution.

Example.

Find the solution of Eqs. (1)–(4) with the initial condition

u(x, 0) = T

, 0 < x < a.

Then g(x) = T

−T

,0< x < a, and the coefﬁcients as determined by Eq. (18)

are

=(T

−T

)

π(2n −1)

Therefore, the complete solution of the boundary value–initial value problem

with initial condition u(x, 0) = T

would be

u(x, t) = T

+(T

−T

)

∞



n=1

2n −1

sin(λ

x) exp



−λ



. (20)

See Fig. 5 for graphs and an animation on the CD.



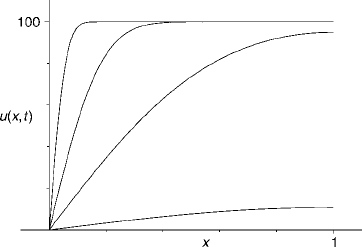
166 Chapter 2 The Heat Equation

Figure 5 Solution of the example, Eq. (20): u(x, t) is shown as a function of x

for various times, which are chosen so that the dimensionless time kt/a

takes the

values 0.001, 0.01, 0.1, 1.0. For the illustration, T

has been chosen equal to 0 and

=100.

Nowthatwehavebeenthroughthreemajorexamples,wecanoutlinethe

method we have been using to solve linear boundary value–initial value prob-

lems. Up to this moment we have seen only homogeneous partial differential

equations, but a nonhomogeneity that is independent of t can be treated by

the same technique.

Summary of Separation of Variables

Prepare

If the partial differential equation or a boundary condition or both are not

homogeneous, ﬁrst ﬁnd a function v(x), independent of t, that satisﬁes the

partial differential equation and the boundary conditions. Since v(x) does not

depend on t, the partial differential equation applied to v(x) becomes an ordi-

nary differential equation. Finding v(x ) is just a matter of solving a two-point

boundary value problem.

Determine the initial value–boundary value problem satisﬁed by the “tran-

sient solution” w(x, t) = u(x, t) −v(x).Thismustbeahomogeneous problem.

That is, the partial differential equation and the boundary conditions (but not

usually the initial condition) are satisﬁed by the constant function 0.

Separate

Assuming that w(x, t) = φ(x)T(t), with neither factor 0, separate the partial

differential equation into two ordinary differential equations, one for φ(x) and

one for T(t), linked by the separation constant, −λ

. Reduce the boundary

conditions to conditions on φ alone.

2.5 Example: Different Boundary Conditions 167

Solve

Solve the eigenvalue problem for φ. That is, ﬁnd the values of λ

for which

the eigenvalue problem has nonzero solutions. Label the eigenfunctions and

eigenvalues φ

(x) and λ

Solve the ordinary differential equation for the time factors, T

(t).

Combine and Satisfy Remaining Condition

Form the general solution of the homogeneous problem as a sum of constant

multiples of the product solutions:

w(x, t) =



(x)T

(t).

Choose the c

so that the initial condition is satisﬁed. This may or may not

bearoutineFourierseriesproblem.Ifnot,anorthogonalityprinciplemust

be used to determine the coefﬁcients. (We shall see the theory in Sections 7

and 8.)

Check

Form the solution of the original problem

u(x, t) = v(x) +w(x, t)

and check that all conditions are satisﬁed.

EXERCISES

See Common Eigenvalue Problems on the CD.

1. Find the steady-state solution of the problem stated in Eqs. (1)–(4).

2. Determine whether 0 is an eigenvalue of the eigenvalue problem stated

in Eqs. (11) and (12). That is, take λ = 0 and see whether the solution is

nonzero.

3. Solve the problem stated in Eqs. (1)–(4), taking f (x ) =Tx/a.

4. Solve the problem stated in Eqs. (1)–(4) if

f (x) =



, 0 < x < a/2,

, a/2 < x < a.

5. Solve the nonhomogeneous problem

∂

∂x

∂u

∂t

−

, 0 < x < a, 0 < t,