Powers D.L. Boundary Value Problems and Partial Differential Equations
Подождите немного. Документ загружается.


168 Chapter 2 The Heat Equation
u(0, t) = T
0
,
∂u
∂x
(a, t) = 0, 0 < t,
u(x, 0) = T
0
, 0 < x < a.
6. Solve this problem for the temperature in a rod in contact along the lateral
surface with a medium at temperature 0.
∂
2
u
∂x
2
=
1
k
∂u
∂t
+γ
2
u, 0 < x < a, 0 < t,
u(0, t) = 0,
∂u
∂x
(a, t) = 0, 0 < t,
u(x, 0) = T
0
, 0 < x < a.
7. Solve the problem
∂
2
u
∂x
2
=
1
k
∂u
∂t
, 0 < x < a, 0 < t,
∂u
∂x
(0, t) = 0, u(a, t) = T
0
, 0 < t,
u(x, 0) = T
1
, 0 < x < a.
8. Compare the solution of Exercise 7 with Eq. (20). Can one be turned into
the other?
9. Solve the problem in Exercise 7 taking T
0
=0and
u(x, 0) = T
1
cos
πx
2a
, 0 < x < a.
10. a. Show that the eigenfunctions found in this section are orthogonal. That
is, prove that
a
0
sin(λ
n
x) sin(λ
m
x) dx =
0 (m = n),
a
2
(m =n)
when λ
n
=
(2n−1)π
2a
.
b. Use the orthogonality relation in part a to justify the formula in
Eq. (18).
11. To justify the expansion of Eq. (17), for an arbitrary sectionally smooth
g(x),
∞
n=1
b
n
sin
(2n −1)π x
2a
=g(x), 0 < x < a,

2.5 Example: Different Boundary Conditions 169
construct the function G(x) with these properties:
G(x) = g(x), 0 < x < a,
G(x) = g(2a −x ), a < x < 2a.
Show that G(x) corresponds to the series
G(x) ∼
∞
N=1
B
N
sin
Nπx
2a
, 0 < x < 2a.
12. Show that the B
N
of the series in the preceding equation satisfy
B
N
=0 (N even), B
N
=
2
a
a
0
g(x) sin
Nπx
2a
dx (N odd).
13. a. Solve this problem over the interval 0 < x < 2a.
∂
2
u
∂x
2
=
1
k
∂u
∂t
, 0 < x < 2a, 0 < t,
u(0, t) = T
0
, u(2a, t) = T
0
, 0 < t,
u(x, 0) = g(x), 0 < x < 2a.
Afunctionf is given over the interval 0 < x < a,andg is an extension
of f defined by
g(x) =
f (x), 0 < x < a,
f (2a − x), a < x < 2a.
b. Explain why the solution of the problem comprising Eqs. (1)–(4) is
exactly the same as the solution of the problem in part
a.
14. In the ceramics industry, the following problem has to be analyzed for
parameter measurement. A cylindrical rod of uniform porous material is
suspended vertically so that its lower end is immersed in water. The cylin-
drical surface and the upper end are sealed — with wax, for example. The
concentration of water in the rod (weight per unit volume) is a function
C(x, t) that satisfies the boundary value problem
D
∂
2
C
∂x
2
=
∂C
∂t
, 0 < x < L, 0 < t,
C(0, t) = C
0
,
∂C
∂x
(L, t) = 0, 0 < t,
C(x, 0) = 0, 0 < x < L.

170 Chapter 2 The Heat Equation
In these equations, D is the diffusion constant, L is the length of the cylin-
der, and C
0
is the saturation concentration, which depends on the porosity
of the material. Find C(x, t).
15. Use the solution of Exercise 14 to find an expression for the total weight
of water absorbed by the rod,
W(t) = A
L
0
C(x, t) dx.
16. A plot of W(t)/C
0
as a function of s =
Dt/L
2
over the range 0 to 2
resembles a slanted line segment joined by a curve to a horizontal line
segment. The slope of the slanted line segment in this graph is approx-
imately 1. Experimenters plot measured values of W(t)/C
0
vs
√
t to get
a similar graph. Then they use the slope of the slanted line segment to
find D.Explainhow.
2.6 Example: Convection
We have seen three examples in which boundary conditions specified either
u or ∂u/∂x. Now we shall study a case where a condition of the third kind
is involved. The physical model is conduction of heat in a rod with insulated
lateral surface whose left end is held at constant temperature and whose right
end is exposed to convective heat transfer. The boundary value–initial value
problem satisfied by the temperature in the rod is
∂
2
u
∂x
2
=
1
k
∂u
∂t
, 0 < x < a, 0 < t, (1)
u(0, t) = T
0
, 0 < t, (2)
−κ
∂u
∂x
(a, t) = h
u(a, t) −T
1
, 0 < t, (3)
u(x, 0) = f (x), 0 < x < a. (4)
We found in Section 2 that the steady-state solution of this problem is
v(x) = T
0
+
xh(T
1
−T
0
)
κ +ha
. (5)
Now, since the original boundary conditions were nonhomogeneous, we
form the problem for the transient solution w(x, t) = u(x, t) −v(x).Bydirect
substitution it is found that
∂
2
w
∂x
2
=
1
k
∂w
∂t
, 0 < x < a, 0 < t, (6)

2.6 Example: Convection 171
w(0, t) = 0, hw(a, t) +κ
∂w
∂x
(a, t) = 0, 0 < t, (7)
w(x, 0) = f (x) −v(x) ≡ g(x), 0 < x < a. (8)
The solution for w(x, t) can now be found by the product method. On the
assumption that w has the form of a product φ(x)T(t), the variables can be
separated exactly as before, giving two ordinary differential equations linked
by a common parameter λ
2
:
φ
+λ
2
φ = 0, 0 < x < a,
T
+λ
2
kT =0, 0 < t.
Also, since the boundary conditions are linear and homogeneous, they can be
translated directly into conditions on φ:
w(0, t) = φ(0)T(t) = 0,
κ
∂w
∂x
(a, t) +hw(a, t) =
κφ
(a) +hφ(a)
T(t) = 0.
Either T(t) is identically zero (which would make w(x, t) identically zero) or
φ(0) = 0,κφ
(a) +hφ(a) = 0.
Combining the differential equation and boundary conditions on φ,weget
the eigenvalue problem
φ
+λ
2
φ = 0, 0 < x < a, (9)
φ(0) = 0,κφ
(a) +hφ(a) = 0. (10)
The general solution of the differential equation is
φ(x) = c
1
cos(λx) +c
2
sin(λx).
The boundary condition at x = 0requiresthatφ(0) = c
1
= 0, leaving φ(x) =
c
2
sin(λx). Now, at the other boundary,
κφ
(a) +hφ(a) =c
2
κλcos(λa) + h sin(λa)
=0.
Discarding the possibilities c
2
= 0andλ = 0, which both lead to the trivial
solution, we are left with the equation
κλcos(λa) + h sin(λa) = 0, or tan(λa) =−
κ
h
λ. (11)

172 Chapter 2 The Heat Equation
A
n 0.2500 0.5000 1.0000 2.0000 4.0000
12.5704 2.2889 2.0288 1.8366 1.7155
25.3540 5.0870 4.9132 4.8158 4.7648
38.3029 8.0962 7.9787 7.9171 7.8857
411.3348 11.1727 11.0855 11.0408 11.0183
514.4080 14.2764 14.2074 14.1724 14.1548
Tab le 2 First five positive solutions of the equation tan(x) =−Ax
Figure 6 Graphs of tan(λa) and −λκ/h. The points of intersection are solutions
of tan(λa) =−λκ/h, eigenvalues of the problem Eqs. (9)–(10). The intersection
at λ =0 corresponds to the trivial solution.
From sketches of the graphs of tan(λa) and −κλ/h (Fig. 6), we see that there is
an infinite number of solutions, λ
1
,λ
2
,λ
3
,..., and that, for very large n, λ
n
is
given approximately by
λ
n
∼
=
2n −1
2
π
a
.
Table 2 shows the first five values of the product λa for several different values
of the dimensionless parameter κ/ha. (More solutions are tabulated in Hand-
book of Mathematical Functions by Abramowitz and Stegun.)
Thus we have for each n = 1, 2,... an eigenvalue λ
2
n
and an eigenfunction
φ
n
(x), which satisfies the eigenvalue problem Eqs. (9) and (10). Accompanying
φ
n
(x) is the function
T
n
(t) = exp
−λ
2
n
kt

2.6 Example: Convection 173
that makes w
n
(x, t) = φ
n
(x)T
n
(t) a solution of the partial differential equa-
tion (6) and the boundary conditions Eq. (7). Since Eqs. (6) and (7) are lin-
ear and homogeneous, any linear combination of solutions is also a solution.
Therefore, the transient solution will have the form
w(x, t) =
∞
n=1
b
n
sin(λ
n
x) exp
−λ
2
n
kt
,
and the remaining condition to be satisfied, the initial condition Eq. (8), is
w(x, 0) =
∞
n=1
b
n
sin(λ
n
x) = g(x), 0 < x < a. (12)
Thus the constants b
n
are to be chosen so as to make the infinite series equal
g(x).
Although Eq. (12) looks like a Fourier series problem, it is not, because λ
2
,
λ
3
, and so forth are not all integer multiples of λ
1
.Ifweattempttousetheidea
of orthogonality, we can still find a way to select the b
n
, for it may be shown by
direct computation that
a
0
sin(λ
n
x) sin(λ
m
x) dx = 0, if n = m. (13)
Then if we multiply both sides of the proposed Eq. (12) by sin(λ
m
x) (where
m is fixed) and integrate from 0 to a,wehave
a
0
g(x) sin(λ
m
x) dx =
∞
n=1
b
n
a
0
sin(λ
n
x) sin(λ
m
x) dx,
where we have integrated term by term. According to Eq. (13), all the terms
of the series disappear except the one in which n = m, yielding an equation
for b
m
:
b
m
=
a
0
g(x) sin(λ
m
x) dx
a
0
sin
2
(λ
m
x) dx
. (14)
By this formula, the b
m
may be calculated and inserted into the formula for
w(x, t). Then we may put together the solution u(x, t) of the original problem
Eqs. (1)–(4):
u(x, t) = v(x) +w(x, t)
= T
0
+
xh(T
1
−T
0
)
(κ +ha)
+
∞
n=1
b
n
sin(λ
n
x) exp
−λ
2
n
kt
.
In Fig. 7 are graphs of u(x, t) for two different values of the parameter κ/ha;
both have initial conditions u(x, 0) = 0.SeeanimationsontheCD.
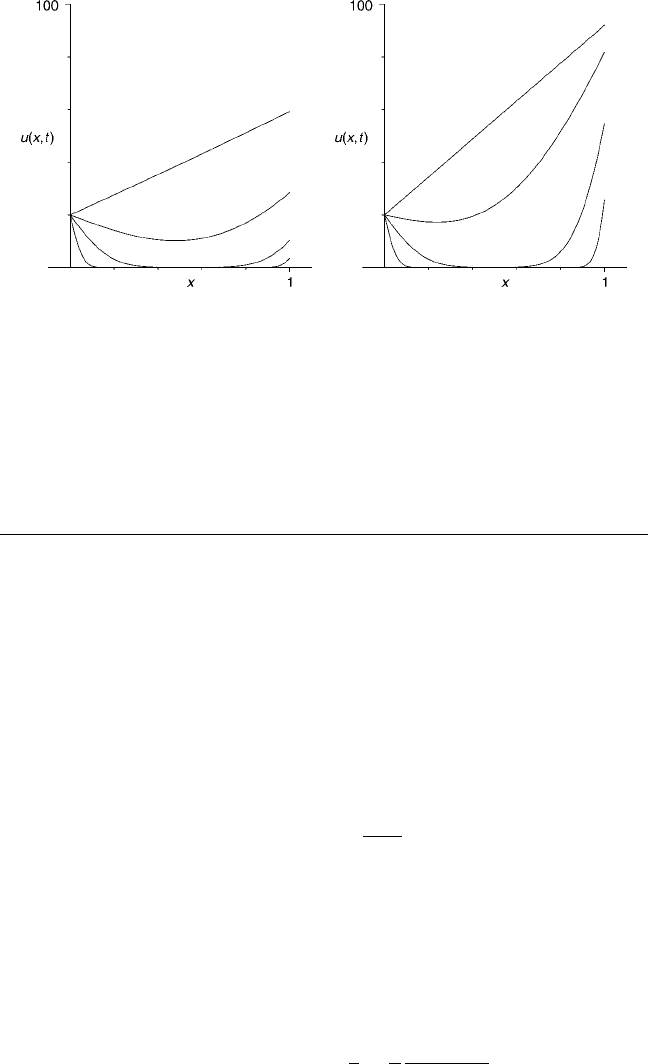
174 Chapter 2 The Heat Equation
(a) (b)
Figure 7 Solution of Eqs. (1)–(4) with T
0
= 20, T
1
= 100, and f (x) = 0. Graphs
(a) and (b) correspond to κ/ha = 0.1andκ/ha = 1.0, respectively. In each case,
u(x, t) is graphed as a function of x for times chosen so that the dimensionless
time kt/a
2
takes on the values 0.001, 0.01, 0.1, 1. Note that both the temperature
and its slope at the right end (x = a) change with time, so the boundary condition
Eq. (3) is satisfied. See animations on the CD.
EXERCISES
1. Sketch v(x) asgiveninEq.(5)assuming
a. T
1
> T
0
; b. T
1
=T
0
; c. T
1
< T
0
.
2. If T
1
> T
0
,asinFig.7,whatisthemaximumvalueofthetemperature
u(x, t) on the interval 0 ≤ x ≤ a at any fixed time t?Thesolutionwillbea
function of T
0
, T
1
and z = κ/ha.
3. Whyhaveweignoredthenegativesolutionsoftheequation
tan(λa) =
−κλ
h
?
4. Derive the formula Eq. (12) for the coefficients b
m
.
5. Sketch the first two eigenfunctions of this example taking κ/h = 0.5(λ
1
=
2.29/a, λ
2
=5.09/a).
6. Ve r i f y t h at
a
0
sin
2
(λ
m
x) dx =
a
2
+
κ
h
cos
2
(λ
m
a)
2
.

2.7 Sturm–Liouville Problems 175
7. Find the coefficients b
m
corresponding to
g(x) = 1, 0 < x < a.
8. Using the solution of Exercise 7, write out the first few terms of the solu-
tion of Eqs. (6)–(8), where g(x) = T,0< x < a.
9. Same as Exercise 7 for g(x) = x,0< x < a.
10. Verify the orthogonality integral by direct integration. It will be necessary
to use the equation that defines the λ
n
:
κλ
n
cos(λ
n
a) +h sin(λ
n
a) =0.
2.7 Sturm–Liouville Problems
At the end of the preceding section, we saw that ordinary Fourier series are
not quite adequate for all the problems we can solve. We can make some gen-
eralizations, however, that do cover most cases that arise from separation of
variables. In simple problems, we often find eigenvalue problems of the form
φ
+λ
2
φ = 0, l < x < r, (1)
α
1
φ(l) −α
2
φ
(l) = 0, (2)
β
1
φ(r) + β
2
φ
(r) = 0. (3)
It is not difficult to determine the eigenvalues of this problem and to show the
eigenfunctions orthogonal by direct calculation, but an indirect calculation is
still easier.
Suppose that φ
n
and φ
m
are eigenfunctions corresponding to different
eigenvalues λ
2
n
and λ
2
m
.Thatis,
φ
n
+λ
2
n
φ
n
=0,φ
m
+λ
2
m
φ
m
=0,
and both functions satisfy the boundary conditions. Let us multiply the first
differential equation by φ
m
and the second by φ
n
,subtractthetwo,andmove
the terms containing φ
n
φ
m
to the other side:
φ
n
φ
m
−φ
m
φ
n
=
λ
2
m
−λ
2
n
φ
n
φ
m
.
The right-hand side is a constant (nonzero) multiple of the integrand in the
orthogonality relation
r
l
φ
n
(x)φ
m
(x) dx = 0, n = m,
176 Chapter 2 The Heat Equation
which is proved true if the left-hand side is zero:
r
l
φ
n
φ
m
−φ
m
φ
n
dx = 0.
This integral is integrable by parts:
r
l
φ
n
φ
m
−φ
m
φ
n
dx
=
φ
n
(x)φ
m
(x) −φ
m
(x)φ
n
(x)
r
l
−
r
l
φ
n
φ
m
−φ
m
φ
n
dx.
Thelastintegralisobviouslyzero,sowehave
λ
2
m
−λ
2
n
r
l
φ
n
(x)φ
m
(x) dx =
φ
n
(x)φ
m
(x) −φ
m
(x)φ
n
(x)
r
l
.
Both φ
n
and φ
m
satisfy the boundary condition at x = r,
β
1
φ
m
(r) +β
2
φ
m
(r) = 0,
β
1
φ
n
(r) +β
2
φ
n
(r) = 0.
These two equations may be considered simultaneous equations in β
1
and β
2
.
At least one of the numbers β
1
and β
2
is different from zero; otherwise, there
would be no boundary condition. Hence the determinant of the equations
must be zero:
φ
m
(r)φ
n
(r) − φ
n
(r)φ
m
(r) = 0.
A similar result holds at x = l.Thus
φ
n
(x)φ
m
(x) −φ
m
(x)φ
n
(x)
r
l
=0,
and, therefore, we have proved the orthogonality relation
r
l
φ
n
(x)φ
m
(x) dx = 0, n = m,
for the eigenfunctions of Eqs. (1)–(3).
We may make a much broader generalization about orthogonality of eigen-
functions with very little trouble. Consider the following model eigenvalue
problem, which might arise from separation of variables in a heat conduction
problem (see Section 9):
s(x)φ
(x)
−q(x)φ(x) + λ
2
p(x)φ(x) = 0, l < x < r,
α
1
φ(l) −α
2
φ
(l) = 0,
β
1
φ(r) + β
2
φ
(r) = 0.

2.7 Sturm–Liouville Problems 177
Let us carry out the procedure used in the preceding with this problem. The
eigenfunctions satisfy the differential equations
sφ
n
−qφ
n
+λ
2
n
pφ
n
= 0,
sφ
m
−qφ
m
+λ
2
m
pφ
m
= 0.
Multiply the first by φ
m
and the second by φ
n
, subtract (the terms containing
q(x) cancel), and move the term containing pφ
n
φ
m
to the other side:
sφ
n
φ
m
−
sφ
m
φ
n
=
λ
2
m
−λ
2
n
pφ
n
φ
m
. (4)
Integrate both sides from l to r, and apply integration by parts to the left-hand
side:
r
l
sφ
n
φ
m
−
sφ
m
φ
n
dx
=
sφ
n
φ
m
−sφ
m
φ
n
r
l
−
r
l
sφ
n
φ
m
−sφ
n
φ
m
dx.
The second integral is zero. From the boundary conditions we find that
φ
n
(r)φ
m
(r) −φ
m
(r)φ
n
(r) = 0,
φ
n
(l)φ
m
(l) − φ
m
(l)φ
n
(l) = 0
by the same reasoning as before. Hence, we discover the orthogonality relation
r
l
p(x)φ
n
(x)φ
m
(x) dx = 0,λ
2
n
=λ
2
m
for the eigenfunctions of the problem stated.
During these operations, we have made some tacit assumptions about in-
tegrability of functions after Eq. (4). In individual cases, where the coefficient
functions s, q,andp and the eigenfunctions themselves are known, one can
easily check the validity of the steps taken. In general, however, we would like
to guarantee the existence of eigenfunctions and the legitimacy of computa-
tionsafterEq.(4).Todoso,weneedthefollowing.
Definition
The problem
(sφ
)
−qφ +λ
2
pφ = 0, l < x < r, (5)
α
1
φ(l) −α
2
φ
(l) = 0, (6)
β
1
φ(r) + β
2
φ
(r) = 0(7)
