Портнягин Н.Н., Пюкке Г.А. Теория и методы диагностики судовых электрических средств автоматизации
Подождите немного. Документ загружается.

81
2.2.2. Построение алгоритма поиска дефектов методом
изоварных характеристик
Далее рассмотрим процедуру разработки алгоритма поиска
дефектов методом изоварных характеристик. Согласно принято-
му иерархическому принципу постепенного увеличения глуби-
ны поиска дефектов следующий этап диагностирования произво-
дится с глубиной поиска до комплектующего элемента.
Для построения алгоритма диагностирования используется
разработанный метод изовар [84–86, 95–98], позволяющий вести
поиск дефек
тов с глубиной до элемента принципиальной схемы.
Объектом диагностирования выбирается элемент функцио-
нальной схемы – СИФУ (без цепей сдваивания), включающий в себя
следующие комплектующие элементы: R41 – МЛТ – 0, 25 100 кОм;
R47 – МЛТ – 2 300 Ом; R50 – МЛТ – 2 300 Ом; V10 – КД 521А;
V16 – КТ 817Б (рис. 2.9).
На рис. 2.10 приведена схема замещения каскада импульсно-
го усилителя с параметрами элементов:
g
1
= g
13
= 1/ R41 = 10
-5
Cм;
g
7
= g
56
= 1/ R47 = 333, 3 · 10
-5
См; g
6
= g
45
= 1/ R50 = 333, 3 · 10
-5
См.
Рис. 2.10. Схема замещения каскада импульсного усилителя
Находятся параметры гибридной схемы замещения через
h-параметры транзистора КТ 817Б:
h
11э
= 0, 25 · 10
3
Ом;
h
12э
= 0, 1;
82
r
б
= 100 Ом;
g
4
= g
27
= g
бэ
= (1 – h
12э
) / (h
11э
– r
б
) = 600 · 10
-5
Cм;
g
5
= g
47
= g
кб
= h
12э
/ (h
11э
– r
б
) = 66, 6 · 10
-5
См;
r
б
= 100 Ом;
g
3
= g
37
= 1 / r
б
= 1000 · 10
-5
См;
g
2
= g
23
= 500 · 10
-5
См.
Затем вводятся проводимости веса: g
8
, g
9
, g
10
= 10
-5
См, позво-
ляющие исключить висячие ветви и регулировать обусловленность
матрицы узловых проводимостей с целью получения оптимальной
изоварной картины. Схему замещения преобразуем, исключив не-
доступный для измерений узел 7 (рис. 2.10) и на основе топологии
электрической цепи записываем матрицу инциденций:
Записывается диагональная матрица проводимостей элемен-
тов ОД, где величина проводимости диода определяется из усло-
вия диагностирования в режиме воздействия на ОД тестовым
сигналом
низкого уровня: diag Y = (100; 500; 39,9; 23, 9; 360; 333, 3;
333, 3; 100; 100; 100) (рис. 2.11).
Рис. 2.11. Преобразованная схема замещения каскада
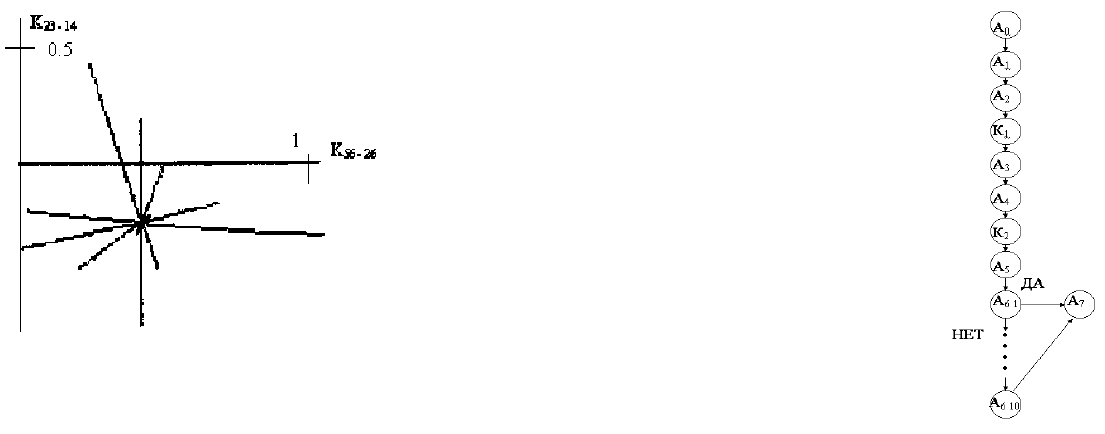
83
Полученные матрицы вводятся в память ПЭВМ. Данные, пе-
речисленные в программе в строке DATA, считываются в ячейки
памяти. После реализации первой программы OTBOR 90A. BAS,
предусматривающей отбор прямых диагностических параметров
по комплексному критерию и критерию эквидистантности изовар,
машина выдает номера входных и выходных плюсов оптималь-
ных
каналов диагностирования (a = 2, b = 3, c = 1, d = 4,
k = 5, l = 6, m = 2, f = 6).
Полученные номера каналов диагностирования, а также мат-
рица инциденций
А и diag Y служат исходными данными для реа-
лизации второй программы построения изовар ISOVAR 90A.BAS,
позволяющей получить карту диагностирования (рис. 2.12), кото-
рая используется для диагностирования в ручном режиме при
проведении диагностического эксперимента.
Следует отметить, что полученная модель является прибли-
женной в силу приближенного характера значений величин пара-
метров СЕ, используемых при построении модели. Для адаптации
модели разр
аботана программа ADAP90, реализующая процесс
постепенного приближения точки равновесного состояния при-
ближенной модели к точке равновесного состояния точной модели.
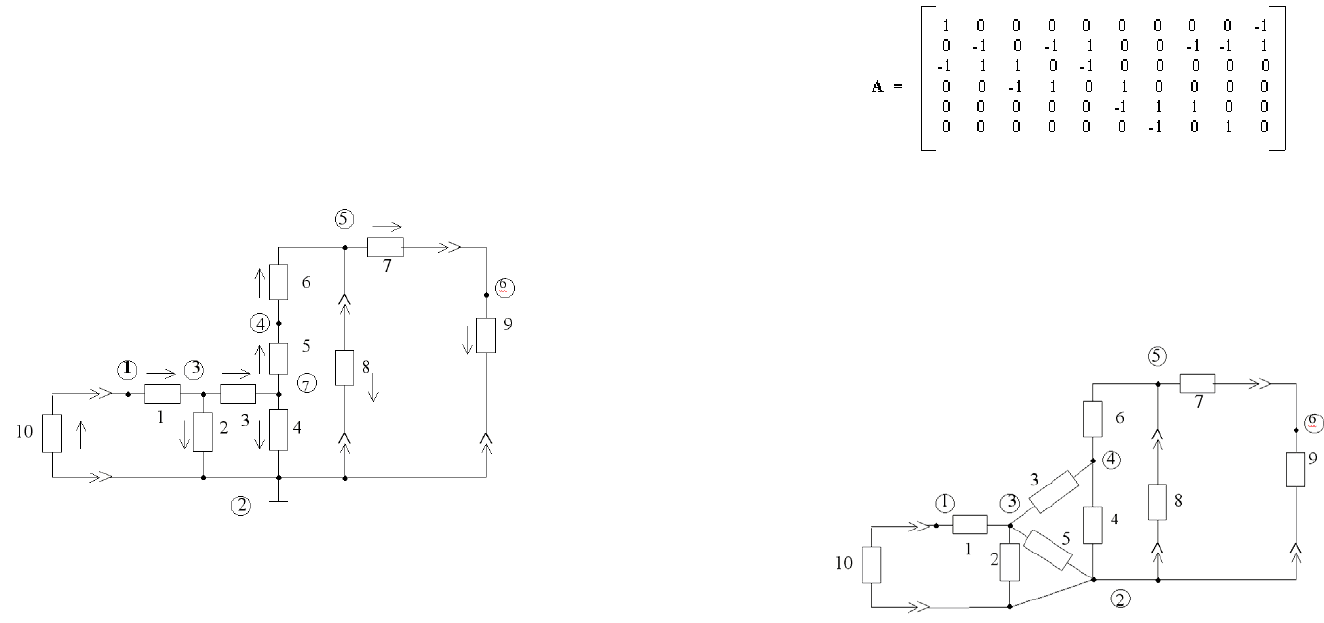
Рис. 2.12. Карта диагностирования импульсного усилителя
Анализ полученной модели позволяет построить алгоритм
поиска дефекта. Алгоритм приведен на рис. 2.13 и включает в се-
бя операторы действия
А
i
и операторы контроля K
i
.
84
Последовательность выполнения операторов следующая:
А
0
– начало алгоритма;
А
1
– подготовка блока усилителя к диагностированию (от-
ключение от системы питания, подключение к источнику тесто-
вых сигналов);
А
2
– подача тестового сигнала на первый информационный
канал;
К
1
– измерение величины сигнала на выходе первого инфор-
мационного канала;
А
3
– вычисление величины коэффициента передачи первого
информационного канала;
А
4
– подача тестового сигнала на второй информативного канал;
К
2
– измерение величины сигнала на выходе второго инфор-
мационного канала;
А
5
– вычисление величины коэффициента передачи второго
информационного канала;
А
6 1
– проверка тождественности первого уравнения диагно-
стической модели;
А
6 m
– проверка тождественности m-го уравнения модели;
А
7
– конец алгоритма.
Рис. 2.13. Алгоритм поиска дефектов импульсного усилителя
85
После определения неработоспособного компонента проис-
ходит его замена. Таким образом, реализация иерархического
принципа уточнения места неработоспособного элемента позво-
ляет выявить дефект с глубиной диагностирования до элемента
принципиальной схемы.
Напомним, что под элементами мы понимаем двухполюсные
компоненты эквивалентной схемы замещения устройства. Оче-
видно, что подобная детализация необходима только в случае
конструктивного исполнения принци
пиальной схемы низкой ин-
теграции. При высокой интеграции появляется возможность
уменьшить глубину поиска дефекта до многополюсной компо-
ненты. Это обстоятельство позволяет рассматривать метод изо-
варных характеристик, как основу для реализации алгоритмов
поиска дефектов в цепях высокой размерности. Однако следует
отметить, что с повышением размерности и снижении мощности
элементов цепи большую роль иг
рают методы логического ана-
лиза и требование увеличения глубины дефекта, как правило, не
выдвигается.
Так, например, диагностика микропроцессорной техники из-
за высокой взаимозаменяемости и унификации компонентов сис-
темы, как правило, требует только обнаружения и поиска неис-
правных модулей, что значительно упрощает реализацию задач
диагностики и сводит их к созданию тестового алгоритмическ
ого
обеспечения
2.2.3. Автоматизация процесса диагностирования методом
изоварных характеристик
Исходными требованиями, предъявляемыми к проектированию
технического средства диагностирования, реализующему алгоритм
диагностирования методом изоварных характеристик, являются дос-
таточно низкая цена в сочетании с широким спектром возможно-
стей, простота строения и невысокая сложность изготовления.
Как правило, достижение обозначенных требований реализу-
ется в результате компромисса между противоре
чивыми требова-
ниями. Принцип построения ТСД определяется решаемыми зада-
чами (поиск дефектов и определение степени работоспособности)
и видом диагностической модели ОД.
86
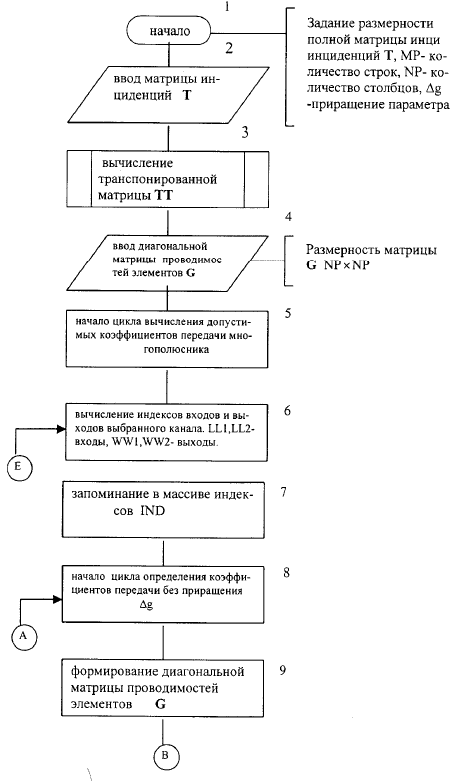
Рис. 2.14а. Алгоритм формирования множества
диагностических параметров (начало)
Структура ТСД, согласно алгоритму диагностирования,
должна реализовывать последовательно-параллельный принцип
обработки информации. Количество каналов обработки информа-
ции равно двум, диагностирование тестовое. Конструктивно ТСД
должно быть выполнено в виде отдельного устройства.
87
После формирования основных требований к ТСД, в соответ-
ствии с классическим подходом к проектированию: метод – алго-
ритм – структура, начинается разработка алгоритма процесса ди-
агностирования.
Рис. 2.14б. Алгоритм формирования множества
диагностических параметров (продолжение)
Разработку алгоритма диагностирования предопределяет про-
цесс разработки диагностического обеспечения (карты изоварных
характеристик), который может быть автоматизирован при реали-
зации методики построения диагностической модели на ЭВМ.
88
Здесь же задаются допуски на диагностические параметры
в виде условий работоспособности (п. 2.1.4). Они оказывают
влияние на выбираемую погрешность измерений, реализуемых
контрольно-измерительным трактом ТСД. Основу алгоритма раз-
работки диагностического обеспечения составляет алгоритм фор-
мирования множества прямых диагностических параметров А1
(рис. 2.14).
Рис. 2.14в. Алгоритм формирования множества
диагностических параметров (окончание)
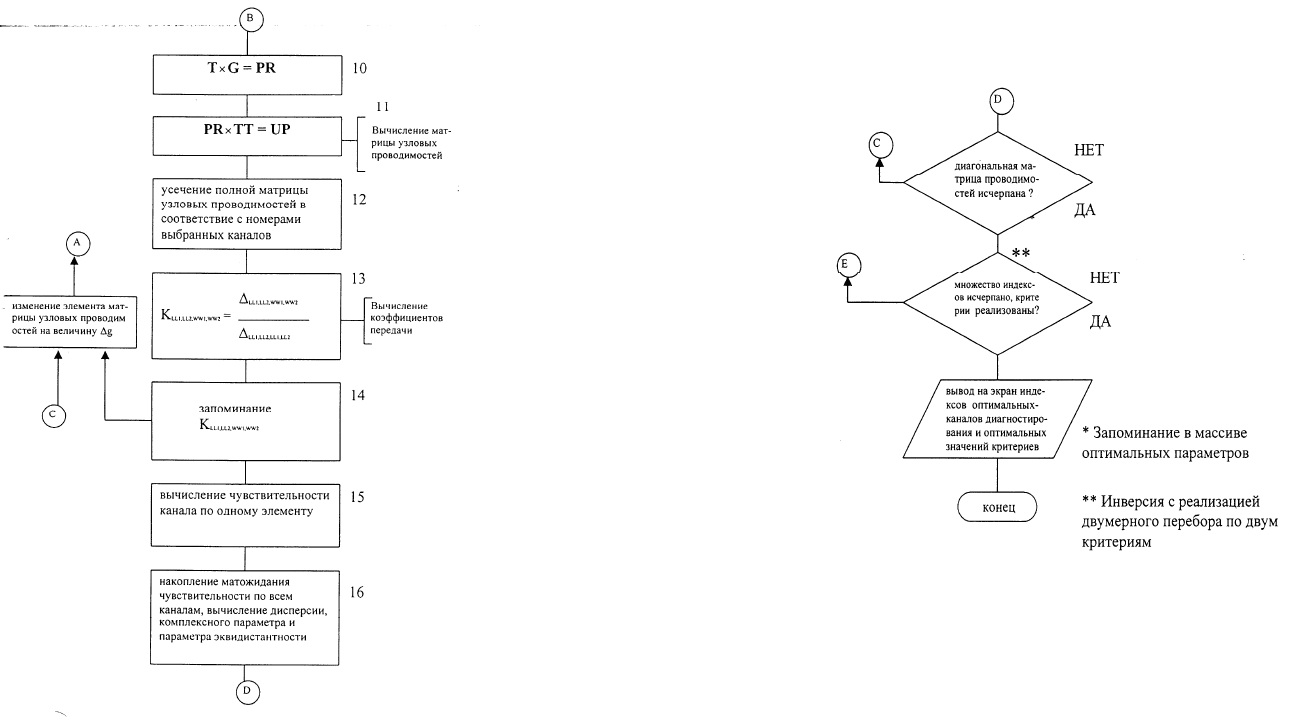
Алгоритм А1 строится на основе разработанной методики от-
бора прямых диагностических параметров и содержит следующие
основные блоки:
1) начало; 2) матрица инциденций (задается набором коэф-
фициентов традиционным способом; рассматривается полная
матрица, позволяющая реализовать вычисление коэффициентов
передачи по единому алгоритму); 3) вычисляется транспониро-
ванная матрица инциденций, используемая для получения матри-
цы узловых проводимостей; 4) диагональная матрица проводимо-
стей з
адается в виде строки длиной NP; 5) в блоке формируется
89
шаг изменения
Δg, задается номер элемента диагональной матри-
цы проводимостей; 6, 7) организуется четырехразрядный счетчик
для перебора индексов многополюсника; 8) организуется цикл
вычисления коэффициентов передачи; 9) формирование матрицы
узловых проводимостей; 10, 11) вычисление полной матрицы уз-
ловой проводимости; 12) усечение матрицы узловой проводимо-
сти для заданных индексов выбранных каналов; 13) вычисление
коэффициента передачи с сохранением; 14) приращение значений
проводимостей; 15) вычисление коэффициентов чувствительно-
сти; 16) накопление резу
льтатов для вычисления критериев мак-
симума интегральной чувствительности и эквидистантности.
Окончание алгоритма (рис. 2.14в) характеризуется блоками
условного перехода, организующими цикл двухмерного перебора
каналов по критериям максимума интегральной чувствительности
и эквидистантности направлений изоварных характеристик.
Алгоритм позволяет обеспечить отбор каналов наблюдения
К1 и К2 за состоянием ОД, при этом полученное семейство изо-
варных характеристик является в смысле выбранных критериев
оптимальным.
90
Глава 3
РАЗРАБОТКА МЕТОДА ИЗОВАРНЫХ ХАРАКТЕРИСТИК
ДЛЯ ДИАГНОСТИРОВАНИЯ МНОЖЕСТВЕННЫХ
ДЕФЕКТОВ
3.1. Вероятностная модель оценки состояния объекта
диагностирования на основе изоварных характеристик
Рассмотренная выше детерминированная модель оценки со-
стояния ОД обладает рядом недостатков:
– потеря значимости результата при увеличении размерно-
сти задачи;
– необходимость перехода к пространству трех измерений
для решения задач пои
ска кратных дефектов;
– низкая эффективность программной реализации алгорит-
мов поиска однократных и многократных дефектов.
Эти недостатки характерны для детерминированных моделей,
и одним из способов их преодоления является введение в рассмот-
рение вероятностных характеристик при оценке состояния системы.
Введем множество
U элементов и элементарных событий,
под которыми будем понимать множество возможных реализаций
численных значений компонент вектора
Y = (y
1
, y
2
, …, y
m
), где
m – количество двухполюсных компонент эквивалентной схемы
замещения;
y
i
– значение диагностического параметра i-ого двух-
полюсника, принадлежащее интервалу
[
]
∞
,0 , введем также мно-
жество событий
А, состоящее из конечного числа событий, число
которых равно
N, событию А
1
– соответствует подмножество U,
элементы которого обеспечивают выполнение системы нера-
венств (2.1), т. е. работоспособное состояние ОД, событию
А
2
соот-
ветствует подмножество
U, на котором нарушается первое нера-
венство системы (2.1), однократный дефект первого компонента, и
далее последовательно перечисляются все возможные состояния
однократных и многократных дефектов.
N – общее количество элементов множества А можно опреде-
лить по формуле:
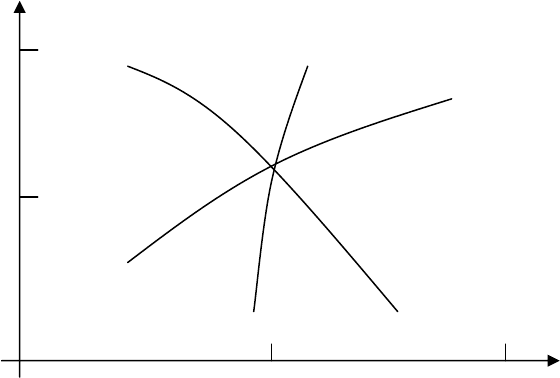
91
.2N
m
=
(3.1)
Для событий множества А определим Р(А
i
) – вероятность на-
ступления
i-го события, удовлетворяющую следующим условиям:
,1)A(P0
i
≤≤ (3.2)
,1)U(P = (3.3)
.)A(P)A(P
N
1i
i
∑
=
= (3.4)
В каждой точке плоскости области определения двух наблю-
даемых диагностических параметров с координатами
К1 и К2
введем счетное множество событий
В
к
, состоящее из подмноже-
ства элементов
U, имеющих координаты К1 и К2 на карте изовар-
ных характеристик, определим условную вероятность
Р(А
i
| В
к
) на-
ступления события А
i
при условии нахождении системы в точке
К
1
, К
2
на карте изоварных характеристик. Множество В
к
состоит
из непересекающихся элементов
В
1
, В
2
, …, В
к
, поэтому справед-
лива формула полной вероятности:
).B|A(P)A(P
k
1k
ii
∑
∞
=
= (3.5)
Введение множества В определяется многозначностью функ-
ции состояния объекта при его наблюдении на плоскости
К1, К2.
Действительно, рассмотрим семейство характеристик из трех
изовар (рис. 3.1). Расположим точку наблюдения
А за состоянием
ОД на изоваре № 2, в эту точку можно переместиться из рабочей
точки
Х минимум двумя способами – изменением параметра g2,
не меняя остальные параметры, либо изменив одновременно
g1 и g3.
Возможны и другие варианты перехода из точки
Х в точку А, на-
пример, можно сначала переместиться по изоваре
g2 в точку С, а
затем из точки
С переместиться в точку Х по двум изоварам g1, g3.
Продолжая делить отрезки
ХС и АС, получим счетное множество
вариантов перемещения из точки
Х в точку А. Таким образом, ка-
ждой точке плоскости
К1, К2 может быть поставлено в соответст-
вие счетное множество векторов состояний ОД, в которых он мо-
92
жет находиться. Если организовать множество
U как счетное, что
нетрудно сделать, введя дискретизацию численных значений его
элементов, можно сказать, что событие
В(К1, К2) наступает, если
вектор
Y имеет координаты К1, К2.
При известных функциях распределения вероятностей
Р(А
i
(К1, К2)), определенной в области допустимых значений пе-
ременных, основная задача диагностики определения состояния
объекта диагностирования по двум измерениям может быть ре-
шена поиском
i, для которого Р(А
i
(К1, К2)) максимальна.
Однако аналитически эту задачу решить практически не
представляется возможным из-за громоздкости выражений, опре-
деляющих связь
К1, К2 с компонентами вектора Y.
Для решения задачи оценки состояния ОД применим метод
статистических испытаний. Для его реализации необходимо
иметь датчик случайных чисел, программу построения семейства
изовар для ОД, программу накопления и отображения результа-
тов применения метода. Современные среды прикладного про-
граммирования, например VISUAL BASIC и EXEL, имеют для
К2
К1
0
1
0.5
0.5 1
. Х
g1 g2 g3
. А
Рис. 3.1. Карта изовар, поясняющая многозначность
точек плоскости К1, К2
.
С
93
этих целей все необходимые средства. Таким образом, метод ста-
тистических испытаний, позволяющий оценить все
m функций
условных вероятностей:
),K,K(f)B/A(P
21ki
= (3.6)
позволяет решать все три перечисленные выше задачи диагности-
рования. Действительно, имея в каждой точке плоскости
К1, К2
значения компонент вектора условных вероятностей нахождения
ОД в каждом из возможных состояний, по максимуму условной
вероятности можно определить наиболее вероятное состояние ОД
в заданной точке плоскости
К1, К2. Таким образом, плоскость К1,
К2
будет разбита на m областей, каждой из которых можно по-
ставить в соответствие наиболее вероятное состояние ОД. Задача
принадлежности текущих измеренных координат
К1, К2 к одной
из выделенных областей эффективно решается с применением
нейросети [76, 113].
3.2. Алгоритм и методика построения
области работоспособности
Приведенный в работах [72, 83, 88] метод оценки состояния
сложной электрической цепи при его реализации требует реше-
ния задачи определения границ области работоспособности
в пространстве признаков диагностических параметров. Однако
детерминированность предложенного в работе [83] метода не по-
зволяет решать эту задачу при средней и высокой размерности
цепей ОД, поэтому рассмотрим вероятностный подход при реше-
нии рассмат
риваемой задачи.
Аналитически условия, определяющие границы области ра-
ботоспособности, выражаются в виде системы неравенств:
y
j
min ≤ y
j
(x) ≤ y
j
max, (3.7)
где y
j
(x) – j-я функция работоспособности; j – индекс опреде-
ляющий номер двухполюсного элемента на эквивалентной схеме
замещения (
J = 1, 2, …, M, где М – общее количество элементов
эквивалентной схемы замещения);
y
j max
, y
j min
– соответственно
наибольшее и наименьшее значение
j-го параметра, х – множест-
во двухполюсных компонентов электрической цепи.
94
В работе [83] показано, что для оценки «холодного» состоя-
ния объекта диагностирования необходимо выделить два наибо-
лее значимых канала и провести с каждым из них опыт холостого
хода. Полученные из опыта значения коэффициентов передач по
каждому из каналов
К1(y
j
) и К2(y
j
) соответственно удовлетворяют
неравенствам (3.8):
1)y(2K1
1)y(1K1
j
j
≤≤−
≤
≤
−
(3.8)
Учитывая более жесткие ограничения (3.1.) получим систему
неравенств (3.9):
max).y(1K)y(1Kmin)y(1K
max),y(1K)y(1Kmin)y(1K
jjj
jjj
≤≤
≤
≤
(3.9)
При построении семейства характеристик К1
j
= f(К2
j
) учет
неравенств (3.9) приведет к ограничению изоварных кривых с
обеих сторон и выделению отрезков кривых, пересекающихся в
исходной рабочей точке, соответствующей номинальным зна-
чениям
у
j
н
(х). Концы отрезков, полученные в результате учета
неравенств (3.9), определяют область работоспособности объ-
екта диагностирования при условии однократного дефекта.
Однако реальные электрические и электронные устройства со-
держат не только двухполюсные компоненты – резисторы, ем-
кости, диоды и т. д., но и многополюсные – трансформаторы,
транзисторы, тиристоры, интегральные микросхемы и другие
сложные электрические и электронные приборы. Выход из
стро
я таких компонентов приводит к кратным дефектам, и не-
посредственное использование системы неравенств (3.9) для
определения области работоспособности в этих ситуациях не-
возможно.
Задача построения области работоспособности при условии
как одиночных, так и кратных дефектов, может быть разрешена в
вероятностной постановке. Для каждой точки пространства зна-
чимых параметров
(К1, К2) должна быть определена функция
р(К1, К2) плотности вероятности нахождения объекта диагности-
рования в работоспособном состоянии и функция
р
н
(К1, К2)
плотности вероятности нахождения объекта диагностирования в
95
неработоспособном состоянии, которые удовлетворяют следую-
щему условию:
.12dK1dK))2K,1K(p)2K,1K(p(
1
1
1
1
H
∫∫
−−
=+ (3.10)
Рис. 3.2. Блок-схема алгоритма построения функции вероятности
работоспособности объекта диагностирования в координатах К1, К2
Кроме того, функция р(К1, К2) имеет постоянное значение
при условии выполнения неравенств (3.9), а при выходе коорди-
нат оценки состояния объекта диагностирования за пределы не-
равенств (3.9) значения функции
р(К1, К2) равны нулю. Для од-
нократных дефектов определение функции
р(К1, К2) не
представляет затруднений, так как интегрирование условия (3.10)
96
осуществляется по всем рабочим отрезкам изоварных характери-
стик. Таким образом,
Р(К1, К2) вероятность нахождения объекта
в работоспособном состоянии равна единице в точках семейства
изоварных кривых в случае однократного дефекта.
Если объект диагностирования может иметь
N-кратные де-
фекты, оценка состояния объекта по двум координатам
К1 и К2
становится неоднозначной: каждой точке оценки состояния соот-
ветствует множество векторов
у
j
(х), а функция р(К1, К2) имеет
максимум в рабочей точке и убывает по мере приближения к гра-
ничным условиям уравнения (3.9).
Естественно предположить что при переходе хотя бы одного
неравенства в равенство значение функции
р(К1, К2) равно нулю.
Рис. 3.3. Функция Р(К1, К2) вероятности работоспособности
трехфазового мостового выпрямителя
Очевидно, что вид функции р(К1, К2) зависит от топологии
элементов объекта диагностирования и их свойств. Если вероятно-
сти возникновения кратных дефектов невелики, функция
р(К1, К2)
близка к константе на всей области (рис. 3.3), если велика вероят-
ность возникновения кратных дефектов, вид функции
р(К1, К2)
зависит от топологии соединения элементов объекта диагностиро-
вания. Для определения области работоспособности в пространстве
К1, К2 в каждой его точке необходимо вычислить значение Р – ве-
роятности нахождения объекта в работоспособном состоянии, вы-
числив отношение значения функции
р(К1, К2) к сумме значений
р(К1, К2) и р
н
(К1, К2). Определив таким образом функцию
Р(К1, К2) и задавшись требуемым пороговым значением величины
вероятности (например,
Р > 0,95), получим область работоспособ-
ности объекта в пространстве выделенных параметров
К1, К2.
97
Аналитическое решение рассматриваемой задачи не найдено,
так как нахождение функций
р(К1, К2) и р
н
(К1, К2) в общем слу-
чае затруднено из-за высокой размерности системы уравнений,
определяющих
К1 и К2 как функции у
j
. В такой ситуации наибо-
лее эффективным является метод статистических испытаний. Для
реализации метода статистических испытаний необходимо иметь:
– детерминированную модель диагностирования, реализо-
ванную в виде программы;
– генератор случайных чисел;
– алгоритм испытаний;
– графическое построение функций плотности вероятности
и вероятности нахождения параметров объекта в области диагно-
стирования.
Детерминированная модель диагностирования с использова-
нием изовар
ных характеристик, реализованная в виде программы
подробно рассмотрена в работе [83]. Генератор случайных чисел
может быть реализован с использованием стандартных функций
языков программирования при решении задач невысокой размер-
ности (до 10 диагностических параметров). При решении задач
высокой размерности малая периодичность стандартных датчиков
случайных чисел не позволит их использовать, и п
отребуется соз-
дание специального генератора случайных чисел.
В качестве алгоритма испытаний используем статистическое
испытание с двумя возможными исходами:
у
j
удовлетворяет сис-
теме неравенств (3.1) и
у
j
не удовлетворяет системе неравенств
(3.1). Допускаем также, что последовательность испытаний мож-
но считать последовательностью независимых испытаний по схе-
ме Бернулли. Тогда в результате каждого испытания с номером
n
будем иметь:
– значения компонент
[у
J
]
n
;
– значения координат на плоскости диагностических при-
знаков
[К1]
n
, [К2]
n
;
– значение функции принадлежности испытания к области
работоспособности
[F]
n
= 1, если система неравенств (1.1) не на-
рушена,
[F]
n
= 0 в противном случае.
Полученные результаты по каждому испытанию накаплива-
ются в два двухмерных массива, по столбцам которых отложены
дискретные значения
[К1]
n
, а по строкам значения [К2]
n
. Таким
образом, по завершении работы алгоритма будут накоплены два
98
массива в дискретных координатах
[К1], [К2], массив численных
значений функции плотности вероятности работоспособности
объекта диагностирования
[p{K1, K2}] и массив численных зна-
чений плотности вероятности неработоспособности объекта ди-
агностирования
[p
н
(К1, К2)]. Следующей процедурой является
вычисление численных значений третьего массива
[P{K1, K2}] –
вероятности работоспособности объекта диагностирования.
Для этого необходимо каждый элемент массива определить
по следующей формуле:
)].2K,1K(p)2K,1K(p/[)2K,1K(p)2K,1K(P
H
+
=
(3.11)
Построив поверхность на основе формулы (3.5) и определив
на ней линии уровней
Р = 0.95; 0.9; 0.8, …, получим границы об-
ласти работоспособности объекта диагностирования для задан-
ного порога вероятности.
Рассмотренный алгоритм для наглядности представим в виде
блок-схемы (рис. 3.2). Детерминированная модель (блоки № 1 – 5),
генератор случайных чисел реализованы в пакете Visual Basic,
процедуры накопления плотности вероятности и построения по-
верхности (блоки № 6 – 10) реализованы в пакете EXEL.
Опробование разработанного алгоритма (рис 3.2) осуществ-
лено на базе подробно рассмотренно
го в работе [77] примера ди-
агностической модели мостового трехфазного выпрямителя, час-
то использующегося в схемах возбуждения судовых синхронных
генераторов и других цепях схем судовой автоматики. В работе
[83] рассмотрен вопрос построения области работоспособности
для случая однократного дефекта, поэтому не было необходимо-
сти использовать вероятностные методы решения задачи. Разрабо-
танн
ый автором алгоритм позволяет решать задачу для дефектов
любой кратности, что особенно важно при диагностировании схем
судовой автоматики, содержащих многополюсные элементы.
На основе полученных результатов можно сделать вывод об
эффективности предлагаемого метода при решении рассматри-
ваемой задачи. Функция вероятности
Р(К1, К2) представленная
на рис. 3.3 в виде поверхности, получена при
N = 1000. Дальней-
шее увеличение
N не приводит к заметным изменениям результата,
временные затраты на выполнение алгоритма для рассматриваемого
примера при
N = 1000 составляют 15 минут, при использовании
99
процессора Intel Pentium с тактовой частотой 166 Мгц. Предлагае-
мый вероятностный подход к оценке состояния объекта диагно-
стирования позволит решить задачу локализации и определения
множественных дефектов, а также задачу оценки и регулирования
запаса работоспособности судовой аппаратуры.
3.3. Диагностика СЭСА методом изоварных
характеристик с применением нейросетей
Эффективность нейросетевого подхода проявляется в долж-
ной мере пр
и решении плохо формализованных задач, для кото-
рых трудно указать последовательность действий, приводящих к
желаемому результату. Следуя работе [76], представим типовые
постановки с анализом их применимости для решения задач ди-
агностики судовых электрических средств автоматизации
(СЭСА).
Распознавание образов
(постановка № 1). Задача состоит в
отнесении входного набора данных, представляющего распозна-
ваемый объект, к одному из заранее известных классов. В число
этих задач входит распознавание рукописных и печатных симво-
лов при оптическом вводе в ЭВМ, распознавание типов клеток
крови, распознавание речи и другие. При диагностировании
СЭСА за распознаваемые образы принимаются неисправности
блоков, узлов, элементов СЭСА, входной набор данных представ-
ляет
ся массивами значений основных диагностических парамет-
ров. При использования метода изоварных характеристик [83]
решение задачи распознавания образов позволит упростить про-
цедуру поиска дефекта.
Кластеризация данных
(постановка № 2). Задача состоит
в группировке
входных данных по присущей им близости. Алго-
ритм определения близости данных (определение расстояния ме-
жду векторами, вычисление коэффициента корреляции и другие
способы) закладывается в нейросеть при ее построении. Сеть кла-
стеризует данные на заранее неизвестное число кластеров. Наи-
более известные применения кластеризации связаны со сжатием
данных, анализом данных и поиском в них закономерностей. При
решении за
дач диагностики СЭСА необходимость кластеризации
очевидна, так как эффективный анализ дефектов, отображенных
в пространстве основных диагностических параметров, возможен
100
при разбиении этого пространства на области соответствующих
состояний объекта диагностирования – работоспособности, одно-
кратных дефектов, многократных дефектов и т. д.
В работе [83] показано, что задачи диагностики СЭСА можно
свести к задаче наблюдения за параметрами четырехполюсника
(один канал наблюдения) или наблюдения за двумя выделенными
четырехполюсниками (два канала наблюдения). В обеих ситуаци-
ях при сред
ней размерности диагностируемой цепи удается све-
сти эту задачу к двухмерному наблюдению, выбрав из возможных
параметров два наиболее значимых с точки зрения критерия ин-
тегральной чувствительности и равномерности распределения
изоварных характеристик по плоскости выбранных диагностиче-
ских параметров. На рис. 3.4 показаны области, выделяемые
в данной плоскости: область работоспособности (в которой не
нару
шены ограничения на диагностические параметры), области
однократных дефектов (в которых нарушено одно из ограниче-
ний), области многократных дефектов (в которых нарушено не-
сколько ограничений). При введении вероятностных переменных
эти области выделяются на основе функций плотности вероятно-
сти нахождения объекта диагностирования в заданном состоянии.
Так, например, область работоспособности мостового трехфазно-
го выпрямит
еля, представленная в работе [111], имеет овальную
форму. Применение нейросетевого подхода (постановка № 1) по-
зволит автоматизировать процесс классификации возникшего де-
фекта, а постановка № 2 позволит провести кластеризацию выде-
ляемых областей. Однако для реализации необходимо выбрать
способ выделения областей.
В настоящее время применяются различные способы реали-
зации запоминания областей. Наиболее употребляемые в настоя-
щее врем
я способы – это выделение областей гиперплоскостями и
покрытие областей гипершарами. Для запоминания одной из ог-
раничивающих область гиперплоскости достаточно сохранения
n + 1 значения, где n – размерность пространства. Соответственно
для запоминания одного гипершара также требуется
п + 1 значе-
ние: координаты центра и радиус.
