Портнягин Н.Н., Пюкке Г.А. Теория и методы диагностики судовых электрических средств автоматизации
Подождите немного. Документ загружается.

61
рядка превращается в полную матрицу узловых проводимостей
s-го порядка путем вычеркивания строк и столбцов, отвечающих
всем полюсам, превращенным во внутренние.
Оставшиеся элементы матрицы находятся по формуле:
Y
ij
’
= Δ
внш (n-1)
ij
/ Δ
внш (n-1)
, (2.7)
где Δ
внш n
– определитель, получаемый из определителя матрицы
узловых проводимостей цепи
n-го порядка путем вычеркивания
строк и столбцов, отвечающих всем оставшимся внешним полю-
сам. Верхние индексы являются восстановительными и показы-
вают, что определитель
Δ
внш (n-1)
ij
получается из определителя
Δ
внш n
путем восстановления строки i и столбца j. Рассмотренная
процедура получения исходной матрицы узловых проводимостей
электрической цепи предполагает, что матрицы узловых прово-
димостей ее отдельных многополюсных компонент известны. Для
простых многополюсных компонент матрицы узловых проводи-
мостей можно получить из анализа их эквивалентных схем.
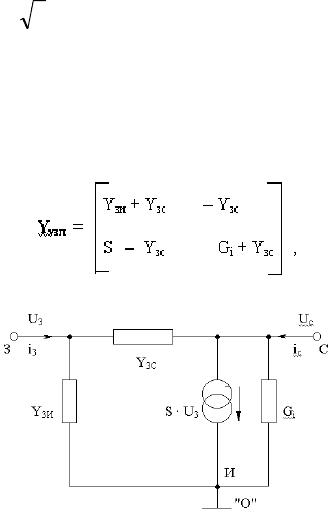
Например: схема полевого транзистора с проводимостями за-
твор – исток
Y
зи
и затвор – сток Y
зс
имеет эквивалентную схему
(рис. 2.2), которой соответствует укороченная матрица узловых
проводимостей, где
S – крутизна характеристики полевого тран-
зистора,
G
i
– внутренняя проводимость полевого транзистора.
В сложных многополюсных компонентах, имеющих один
внутренний полюс, связь между токами и напряжениями внеш-
них полюсов определяется путем исключения из исходной
матрицы строки и столбца, отвечающих этому полюсу, и пере-
расчета оставшихся элементов матрицы по формуле (2.1). Та-
кое преобразование следует из необходимости иметь для диаг-
ностирования матрицу, включающую тольк
о доступные для
контроля полюсы съема информации. В сложных многополюс-
ных компонентах, имеющих ряд внутренних полюсов, постав-
ленная задача достигается путем использования их основных
внешних параметров.
Следует отметить, что использование тестового диагностиро-
вания элементов требует проведения
n измерений и число комму-
таций определяемых топологией цепи. Такой переход системы
в новое состояние подтверждает взаимно-однозначное соответст-
вие между координатами точки состояния
(К
1,
К
2
) и наборами
численных значений диагностических параметров, которое может
62
быть задано параметрически:
К
1
= F(g
1
, g
2
, …, g
m
); К
2
= F(g
1
, g
2
, …, g
m
). (2.8)
Попеременное фиксирование в различных сочетаниях пара-
метров в системе (2.8) позволяет получить параметрически задан-
ное семейство изовар:
К
1
= F
1
(g
1
); К
1
= F
2
(g
2
); …. К
1
= F
m
(g
m
);
К
2
= F
1
(g
1
); К
2
= F
2
(g
2
); …. К
2
= F
m
(g
m
). (2.9)
Cуть метода коррекции состоит в следующем. Сначала пер-
вая система соотношений (2.8) исследуется по критерию мини-
мального расстояния
d при вариации параметра g
1
:
min (d = {[К
2 изм
– К
2
(g
i
)]
2
+ [К
1 изм
– К
1
(g
i
)]
2
}); (2.10)
где К
1 изм
, К
2 изм
– координаты точки равновесного состояния уточ-
ненной модели;
К
2
(g
i
), К
1
(g
i
) – текущие координаты точки равно-
весного состояния приближенной модели;
g
i
– варьируемый па-
раметр;
i = 1, …, m.
Рис. 2.2. Эквивалентная схема полевого транзистора
Методами математического анализа выражение исследуется
на экстремум (находятся производные, приравниваются к нулю,
находится точка минимума). Выражение для первой производной
разрешается относительно искомого параметра
g
1
. Затем вторая
63
и последующие системы подвергаются аналогичному преобразо-
ванию, в результате чего записывается набор уточненных значений
параметров СЕ
g
1
,
g
2
, …..., g
m
, которые будут уточненными значе-
ниями элементов диагональной матрицы проводимостей. На осно-
ве уточненных данных строится точная диагностическая модель.
Таким образом, использование метода постепенных прибли-
жений позволяет, не нарушая целостности ОД, расчетным спосо-
бом определить параметры СЕ, точные данные по которым, как
правило, отсутствуют. Для адаптации моделей электрических це-
пей средней и высокой размерности авторами р
азработана про-
грамма ADAP 400 [93].
Далее рассмотрим использование различных режимов диаг-
ностирования и связанные с ними различные возможности диаг-
ностирования. При диагностировании в режиме постоянного тока
на вход канала диагностирования подается тестовый сигнал по-
стоянного уровня. Подключение диагностируемой электрической
цепи к источнику постоянного тока требует соответствующей ме-
тодики определения ве
личин проводимостей p-n-переходов полу-
проводниковых приборов, используемых при построении диагно-
стической модели ОД.
Исходными данными здесь являются вольтамперные харак-
теристики
p-n-переходов. Однако величины напряжений (и их
полярность) на
p-n-переходах априори не известны (т. к. не из-
вестны номера полюсов отобранных каналов диагностирования).
Это вносит некоторую неопределенность, для снятия которой
возможны следующие подходы:
– выбор малой величины уровня тестового сигнала, позво-
ляющей регистрировать сопротивление постоянному току
p-n-перехода полупроводникового прибора при любой полярно-
сти напряжения, приложенного к нему;
– выбор достаточно высокого уровня тестового сигнала, при
котором определяются прямые и обратные сопротивления
p-n-переходов постоянному току.
В первом случае независимо от выбранных номеров полюсов ка-
налов диагностирования и полярности приложенного напряжения
малая проводимость
p-n-перехода в области начала координат вольт-
амперных характеристик служит признаком его работоспособности.
Во втором случае необходимо учитывать полярность напряже-
ния на
p-n-переходах, а взаимные проводимости полюсов опреде-
64
лять в режиме постоянного тока из вольтамперных характеристик
при известных значениях величин напряжений на полюсах.
В силу того что построенная на определенных таким образом
численных значениях проводимостей СЕ модель будет последст-
вии подвергнута адаптации, в качестве первого приближения при
вычислении параметров СЕ может быть использована гибридная
схема замещения биполярного транзистора, аналитически связан-
ная с сист
емой
h-параметров. Соответственно упрощается схема
замещения транзистора (рис. 2.2), где:
g
бэ
= (1 – h
12э
) / (h
11
– r
б
’
);
g
кб
= h
12э
/ (h
11э
– r
б
’
); r
б
’
.
Следует отметить, что точка 4 (рис. 2.2) недоступна для из-
мерений, но схему можно преобразовать, превратив полюс 4 во
внутренний. Для этого в исходной матрице узловых проводимо-
стей четырехполюсной компоненты вычеркивается 4-я строка
и 4-й столбец, а остальные элементы пересчитываются по формуле:
g
ij
’
= g
ij
– g
ik
g
kj
/ g
kk
. (2.10)
При таком преобразовании, эквивалентном в отношении рас-
пределения потенциалов по полюсам цепи, порядок матрицы уз-
ловых проводимостей цепи понижается на единицу. Понижение
порядка матрицы узловых проводимостей упрощает вычисление
ее определителя и его алгебраических дополнений, т. е. упрощает
определение функций цепи.
С другой стороны, количество уравнений в модели остается
прежним, но параметры СЕ преобр
азованной схемы становятся
взаимозависимыми. Это приводит к тому, что при вариации па-
раметра одной структурной единицы гибридной схемы замеще-
ния необходимо рассматривать вариации параметров сразу трех
СЕ схемы преобразованной. Это выходит за рамки задач поиска
одиночных дефектов методом изовар.
Следовательно, преобразования с целью понижения порядка
матрицы узловых проводимостей компонент целесообразно исп
оль-
зовать при рассмотрении задачи поиска множественных дефектов.
Следует отметить, что использование тестового сигнала ма-
лого уровня упрощает процедуру построения предварительной
диагностической модели, т. к. снимает проблему предварительно-
го определения величин проводимостей
p-n-переходов полупро-
водниковых приборов, но накладывает ограничения на возможно-
сти определения проводимостей реактивных элементов.
65
Наличие в ОД дискретных элементов не требует корректи-
ровки метода, т. к. тестовый сигнал постоянного уровня не обес-
печивает динамики опрокидывания дискретного элемента, а толь-
ко фиксирует величину проводимости в одном из устойчивых
состояний, значение которой для работоспособной компоненты
всегда известно.
Таким образом, применение тестового сигнала малого уровня
снимает проблемы, связанные с нели
нейностью, взаимозависимо-
стью и дискретностью СЕ, но накладывает ограничения на воз-
можности идентификации параметров реактивных компонент.
При диагностировании в режиме переменного тока частота
тестового сигнала выбирается из условия обеспечения малого
разброса проводимостей реактивных элементов и соизмеримости
ее с проводимостью элементов, имеющих чисто активное сопро-
тивление. Выполнение этих условий необходимо для полу
чения
оптимальной изоварной картины, зависящей от обусловленности
матрицы узловых проводимостей цепи.
Погрешности решения задач диагностики методом изовар
оказываются большими для тех цепей, у которых искомые матри-
цы узловых проводимостей хуже обусловлены. Это могут быть
цепи с проводимостями, значения которых существенно меньше
значений проводимостей остальной части цепи.
Это может приводить к с
мещению точки равновесного состоя-
ния к границе пространства диагностирования и сжатию изоварной
картины, что повлияет на разрешающую способность метода.
Как уже отмечалось, предварительная диагностическая мо-
дель может быть построена на основе приближенных данных
о численных значениях параметров СЕ диагностируемой элек-
трической цепи.
Для получения точной модели необходимо произвести уточ-
нение на
чальных значений параметров СЕ объекта диагностиро-
вания. Для достижения этой цели можно применить либо метод
постепенного приближения, либо метод матричных преобразова-
ний, приведенный в п. 1.3.4.
Однако при косвенном определении параметров возникают
погрешности, обусловленные не только ошибками измерений, но и
структурно-топологическими особенностями исследуемых цепей.
Если уровень возможных ошибок измерений часто уд
ается
компенсировать повышением класса точности измерительных
66
приборов, то погрешности, связанные со структурно-
топологическими особенностями ОД накладывают определенные
ограничения на диапазон возможностей рассматриваемого метода.
В этой ситуации представляет интерес оценка относительной
погрешности определения матрицы узловых проводимостей, ко-
торая может быть получена при использовании мультипликатив-
ных норм, связанных с мерой обусловленности матрицы.
Так, при построении матрицы узловых проводимостей мето-
дом матричных преобразований
Y
узл.
U = 1 (п. 1.3.4) мерой обу-
словленности матриц узловых напряжений, сопротивлений и про-
водимостей являются числа обусловленности
α
u
:
α
z
, α
y
, α
u
= α
z
= α
y
= ║U║•║U
-1
║=║Z║•║Z
-1
║=║Y║•║Y
-1
║,
(т. к.
U = Z = Y
-1
).
Если эта мера будет близка к единице (α > 1), то матрица хо-
рошо обусловлена и относительная погрешность определения
матрицы узловых проводимостей будет мала.
2.2. Методика диагностирования
(на примере диагностики СИФУ)
В основу методики диагностирования СЭУ положен иерар-
хический принцип постепенного увеличения глубины поиска де-
фекта в соответствии с оценкой целесообразности реализации за-
данного уровня глубины поиска и возможностью представления
ОД нескольк
ими уровнями деления.
В процессе такого деления на каждом этапе диагностирова-
ния происходит постепенное уточнение места дефекта: сначала
определяется неработоспособный блок (конструктивно оформ-
ленный элемент ОД), затем производится диагностирование вы-
явленного блока с глубиной поиска до элемента функциональной
схемы и т. д. Завершающий этап состоит в диагностировании на
уровне элемента фу
нкциональной схемы с глубиной поиска до
элемента принципиальной схемы методом изовар.
На различных уровнях глубины поиска используются раз-
личные диагностические модели: так, при поиске дефектов с точ-
ностью до блоков, микроблоков, сборок и т. д. целесообразно ис-
пользовать функциональную модель, для логического анализа
которой используется таблица состояний [53, 73, 75].
67
При последующем увеличении глубины поиска можно ис-
пользовать метод изовар, позволяющий идентифицировать со-
стояние ОД с глубиной поиска дефектов до элемента принципи-
альной схемы.
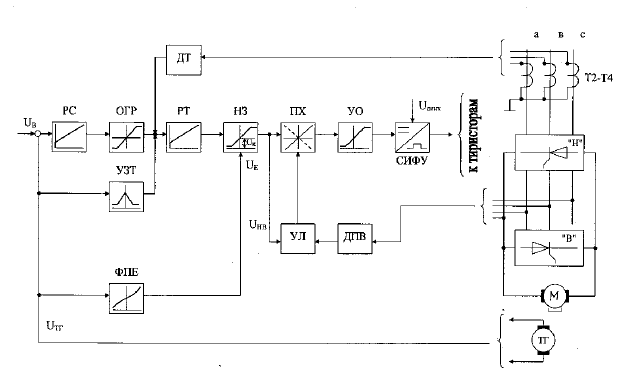
В качестве примера рассмотрим судовой тиристорный элек-
тропривод (СТЭП), исходной формой представления которого
выберем функциональную схему (рис. 2.3), где:
– РС, РТ – регуляторы скорости и тока;
– CИФУ – система импу
льсно-фазового управления;
– Н и В – трехфазные мостовые комплекты тиристоров;
– М – электродвигатель постоянного тока независимого
возбуждения;
– ДТ– датчик тока;
– ТГ – тахогенератор, используемый в качестве датчика тока;
– ФПЕ – функциональный преобразователь ЭДС двигателя;
– НЗ – нелинейное звено;
– УЛ – логическое устройство раздельного управления;
– ПХ – переключатель хар
актеристик;
– УЗТ – узел токоограничения, осуществляющий дополни-
тельное ограничение тока в функции скорости;
– ДПВ – датчик проводимостей вентилей;
– УО – управляющий орган СИФУ, осуществляющий уста-
новку и ограничение начального угла регулирования.
Рис. 2.3. Функциональная схема СТЭП
68
Фазовый сдвиг импульсов относительно силового напряже-
ния на тиристорах пропорционален напряжению, поступающему
на СИФУ от УО. Логическое устройство раздельного управления
служит для формирования сигналов, управляющих ключами В
и Н в переключателе характеристик, а также в датчике тока и це-
пи импульсных трансформаторов.
Контроль отсутствия тока через тиристоры производится
ДПВ. Выходное напряжение регу
лятора скорости ограничивается
уровнем насыщения операционного усилителя. Регулятор тока
формирует напряжение, пропорциональное разности сигналов
задания на ток и отрицательной обратной связи по току. Нели-
нейное звено суммирует выходное напряжение регулятора тока
U
рт
, пропорциональное току двигателя, и напряжение U
е
обрат-
ной связи по ЭДС с разными коэффициентами передачи. Коэф-
фициент передачи НЗ по входу является линейным, имея зависи-
мость, обратную коэффициенту передачи ТП в зоне прерывистого
тока. Коэффициент передачи НЗ по входу является постоянным.
Сигнал U
е
формирует ФПЕ, имеющий характеристику, близкую к
функции арксинуса, т. е. обратную к регулировочной характери-
стике ТП. Этим осуществляется приведение сигнала ТГ, пропорцио-
нального ЭДС двигателя к входу СИФУ. Разнополярное напряжение
управления нелинейного звена преобразуется переключателем ха-
рактеристик в однополярное, т. е. в статическом режиме работы
привода на УО подается напряжение только от
рицательной поляр-
ности независимо от работающего комплекта тиристоров.
В состав электропривода входят два контура обратной связи
по току и скорости, причем эти контуры охватывают друг друга.
Контур скорости охватывает практически все элементы функцио-
нальной схемы ЭП.
2.2.1. Построение логической модели диагностики СИФУ
Наличие контура обратной связи снижает чувствительность
метода при идентификации состоян
ия ОД по выходному сигналу,
поэтому применение логической модели для решения задач диаг-
ностирования без обрыва цепи обратной связи не обеспечит необ-
ходимой глубины поиска. Учитывая эти особенности, для реше-
ния задачи поиска дефектов до функционального элемента
предлагается делать обрыв между УО и СИФУ, а выходной сиг-
69
нал от УО на СИФУ
U
у
заменить тестовым напряжением, соот-
ветствующим допустимому напряжению (0 – 10 в). Преимущест-
вом этой точки обрыва является то, что она позволяет раскрыть
оба контура сразу. После этого производится построение логиче-
ской модели ЭП для поиска дефектов с глубиной до элемента
функциональной схемы. Процесс построения логической модели
достаточно полно рассмотрен в работах [53,99], поэтому здесь
отметим только особенности ЭП и необходимые ус
ловия допу-
щений для построения его диагностической модели:
– если хотя бы один блок ЭП неработоспособен, то ЭП счи-
тается неработоспособным;
– для всех входов и выходов блоков функциональной схемы
ЭП существуют допустимые пределы параметров. Выход за до-
пустимые пределы параметров означает переход ЭП в неработо-
способное состояние;
– имеетс
я возможность осуществлять контроль за каждым
блоком;
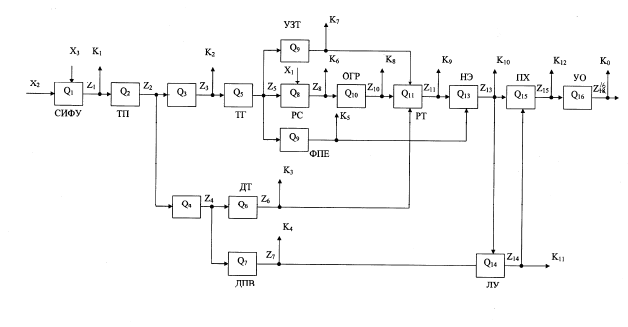
– двигатель постоянного тока заменяется в логической мо-
дели двумя блоками Q
3
и Q
4
так как его выходными параметрами
являются ток и скорость вращения;
– остальные блоки функциональной схемы ЭП заменяются
соответствующими блоками логической модели (CИФУ –
Q
1
,
ТП –
Q
2
, ТГ – Q
5
, ДТ – Q
6
, ДПВ – Q
7
, РС – Q
8
, УЗТ – Q
9
, ОГР – Q
10
,
РТ –
Q
11
, ФПЕ – Q
12
, НЭ – Q
13
, ЛУ – Q
14
, ПХ – Q
15
, УО – Q
16
).
Рис. 2.4. Логическая модель поиска дефектов
70
Логическая модель диагностики СИФУ, построенная по
функциональной схеме ЭП с обрывом между блоками УО и
СИФУ, показана на рис. 2.4.
При анализе логической модели для решения задачи поиска
дефектов необходимо построить таблицу состояний. При по-
строении таблицы состояний используются следующие основные
положения. В качестве прямых диагностических показателей вы-
бираются выходы
Z
i
, i = 1, …, 16 всех элементов логической мо-
дели, которые представляют собой СЕ объекта.
При проверке выход оценивается по двоичной системе: еди-
ница – если реакция выхода допустимая, ноль – если реакция вы-
хода недопустимая. Реакция работоспособного элемента является
допустимой (неработоспособного недопустимой). Входное воз-
действие, приложенное к работоспособному элементу для полу-
чения допустимой реакции, является допустимым воздействием.
Допу
стимая реакция любого элемента получается только в том
случае, если все воздействия на элемент являются допустимыми.
Состояние ОД оценивается вектором
S, в котором компонен-
тами являются 1 или 0, соответствующие оценке состояния функ-
ционального элемента (
S
0
– все элементы работоспособны,
S
1
– элемент Q
1
неработоспособен, S
2
– элемент Q
2
неработоспо-
собен и т. д.).
В таблице состояний число столбцов соответствует числу пря-
мых диагностических признаков (числу проверок
π
i
, i = 1, …, 16).
В каждой строке таблицы состояний располагаются результаты
проверок, соответствующие определенному состоянию ОД при
недопустимой реакции одного из элементов [65].
Для заполнения таблицы состояний необходимо выполнить
анализ логической модели. Для этого записываются функции ус-
ловий работы блоков модели:
F
1
= X
1
X
2
; F
2
= Z
1
; F
3
= F
4
= Z
2
;
F
5
= Z
3
; F
6
= F
7
= Z
4
; F
8
= X
1
Z
5
; F
9
= F
12
= Z
5
; F
10
= Z
8
;
F
11
= Z
6
Z
9
Z
10
; F
13
= Z
11
Z
12
; F
14
= Z
7
Z
13
;
F
15
= Z
13
Z
14
; F
16
= Z
15
,
где:
X
1
, X
2
, X
3
– внешние тестовые воздействия. Соответственно
функции выходов блоков модели:
Z
1
= Q
1
X
2
X
3
; Z
2
= Q
2
Z
1
;
Z
3
= Q
3
Z
2
; Z
4
= Q
4
Z
2
; Z
5
= Q
5
Z
3
; Z
6
= Q
6
Z
4
; Z
7
= Q
7
Z
4
;
Z
8
= Q
8
X
1
Z
5
; Z
9
= Q
9
Z
5
; Z
10
= Q
10
Z
8
; Z
11
= Q
11
Z
6
Z
9
Z
10
; Z
12
= Q
12
Z
5
;
Z
13
= Q
13
Z
11
Z
12
; Z
14
= Q
14
Z
7
Z
13
; Z
15
= Q
15
Z
13
Z
14
; Z
16
= Q
16
Z
15.
Результаты анализа модели сведены в таблицу 2.1. Анализ
таблицы состояний проводится с целью минимизации множества
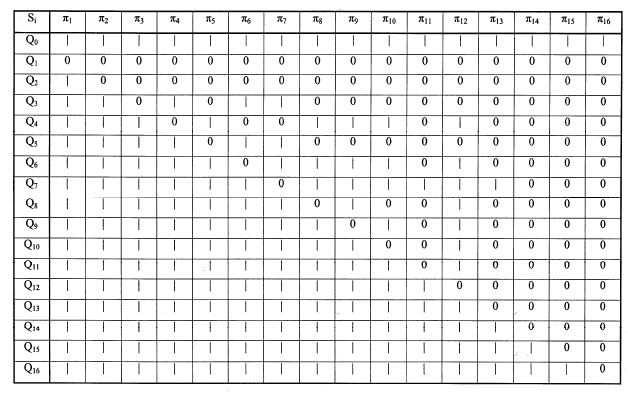
71
проверок, необходимых для однозначной идентификации оди-
ночных дефектов в ОД.
Для модели данного ЭП проверка работоспособности состоит
в контроле сигнала на выходе УО
(π
16
) при подаче тестовых сиг-
налов
X
1
, X
2
, X
3
.
Таблица 2.1
Состояние логической модели
Результаты полученного диагноза позволяют сделать заклю-
чение о целесообразности проведения процедуры поиска нерабо-
тоспособного блока. Если нарушение работоспособности уста-
новлено, то строится алгоритм поиска дефектов с глубиной
поиска дефектов до одного блока логической модели.
Алгоритм должен различать каждую пару дефектов, т. е. ре-
зультаты входящих в алгоритм элементарных проверок должны
быть разными в каждо
м неработоспособном состоянии. Такую
совокупность будем называть различающей совокупностью кон-
трольных точек.
Задача построения алгоритма поиска дефектов состоит в оп-
ределении такой минимальной совокупности и ее упорядочении.
Для определения этой минимальной совокупности, достаточной
для обнаружения отказавшего элемента, попарно сравнивают ре-
72
зультаты проверок при всех состояниях ОД. Результаты сравне-
ния заносятся в новую таблицу, в которой в каждой строке стоит
1 или 0. Ноль – если проверка дала одинаковые результаты,
и единица – если проверка дала различные результаты.
Количество строк в таблице определяется комбинаторно
и равно количеству пар сочетаний неработоспособных состояний:
М
стр.
= С
Q
2
,
где Q – количество неработоспособных состояний. Количество
столбцов определяется количеством возможных проверок
π
i
.
Анализ этой таблицы состоит в определении минимально
возможного количества столбцов, при наложении которых логи-
ческая сумма по каждой строке равна единице. Это дает возмож-
ность определить минимальную совокупность различающих про-
верок, регистрирующую все пары сочетаний неработоспособных
состояний.
Однако в нашем случае имеется возможность определить ми-
нимальную различающую совокупность контрольных выходов
для поиска де
фектов с помощью логического анализа результатов
таблицы 2.1. Проверка
π
1
различает состояние Q
1
cо всеми други-
ми
Q
2
– Q
16
. Проверка π
2
различает состояние Q
2
со всеми осталь-
ными (кроме
Q
1
, но с Q
1
, Q
2
различается уже в проверке π
1
). Сле-
дующая проверка
π
3
различает состояние Q
3
со всеми
остальными, кроме
Q
1
и Q
2
, но они различаются с Q
3
в проверках
π
1
и π
2
и т. д.
Однако есть проверки, которые, кроме очередной последова-
тельной совокупности разрешения, имеют различия, дублирую-
щие некоторые разрешения предыдущих проверок. Так, напри-
мер, проверка
π
2
может быть исключена как дублирующая, если
найдется другая проверка, которая, кроме основной последова-
тельности разрешения, имеет разрешение, различающее состоя-
ния
Q
1
и Q
2
. Такие проверки есть: это проверки π
4
, π
6
, π
7
.
Тогда выбирается одна из проверок, например
π
6
, которая
становится обязательной и при дальнейшем анализе не исключа-
ется. Проверка
π
3
тоже становится обязательной, т. к. регистриру-
ет различие состояния
Q
2
c Q
4
, Q
5
, …, Q
16
.
Рассуждая аналогичным образом, можно исключить также
проверки
π
4
и π
5
(π
8
, имеющая разрешение состояний Q
8
и Q
9
в проверке
π
10
, все же не исключается, т. к. не имеет разрешения
73
в состояниях
Q
8
и Q
10
последующей проверки π
9
и никакие другие
проверки этого разрешения не дадут).
Рис. 2.5. Алгоритм поиска дефектов
Таким образом, минимальная, необходимая совокупность
контрольных точек, выбранных для поиска дефектов ЭП, состоит
из выходов:
Z
1
, Z
3
, Z
6
, Z
7
, Z
8
, Z
9
, Z
10
, Z
11
, Z
12
, Z
13
, Z
14
, Z
15
.
Эту совокупность следует упорядочить по степени уменьше-
ния вероятности возникновения дефектов соответствующих
функциональных элементов. Если считать, что вероятность воз-
никновения дефектов всех элементов ЭП одинакова, то упорядо-
чение можно проводить по следующему правилу: порядок кон-
трольной точки определяется числом нулей в соответствующем
столбце таблицы состояний, причем упорядочение проводится по
степени увеличения чи
сла нулей столбца. Действительно, при
упорядочении по этому правилу для нахождения каждого дефекта
требуется только часть совокупности контрольных точек. Напри-
мер, допустим, дефект возник в элементе
Q
3
. Тогда достаточно
производить контроль
Z
1
, Z
3
, Z
6
и нет необходимости производить
контроль всей совокупности. После этого можно остановить про-
74
цесс поиска и переходить к восстановлению
Q
3
.
Таким образом уменьшаются затраты на контроль и время
поиска дефектов в целом. Тогда поиск дефектов ЭП осуществляется
в следующем порядке:
Z
1
, Z
3
, Z
6
, Z
7
, Z
12
, Z
8
, Z
9
, Z
10
, Z
11
, Z
13
, Z
14
, Z
15
.
Номера контрольных точек для поиска дефектов ЭП до функцио-
нального элемента показаны на рис. 2.4.
Алгоритм поиска дефектов ЭП до функционального элемен-
та, построенный по полученным результатам анализа ДМ приве-
ден на рис. 2.5.
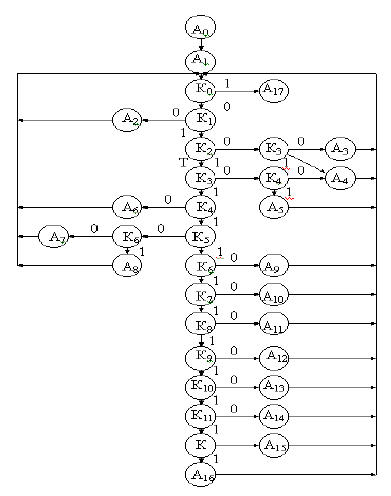
В алгоритме используются:
А
i
– операторы действия, К
j
– операторы контроля (К
j
= 1, ес-
ли значение соответствующего
Z
j
в норме; К
j
= 0, если значение Z
j
за допустимыми пределами).
Алгоритм включает следующие операторы:
А
0
– начало алгоритма;
А
1
– подготовка ЭП и ТСД к диагностированию (размыкание
контуров обратных связей, подача необходимых тестовых сигна-
лов и т. д.),
К
0
– контроль работоспособности ЭП (К
0
= 1, если ЭП рабо-
тоспособен,
К
0
= 0, если ЭП неработоспособен);
К
1
– контроль Z
1
– выходов СИФУ;
А
2
– поиск и устранение дефектов СИФУ;
К
2
– контроль Z
3
– напряжения двигателя постоянного тока;
А
3
– поиск и устранение дефектов тиристорного преобразователя;
К
3
– контроль Z
6
– выходного напряжения датчика тока;
А
4
– нахождение и устранение дефектов двигателя;
К
4
– контроль Z
7
– выходного напряжения датчика проводи-
мости вентилей;
А
5
– поиск и устранение дефектов датчика тока;
А
6
– поиск и устранение дефектов ДПВ;
К
5
– контроль Z
12
– выходного напряжения ФПЕ;
К
6
– контроль Z
8
– выходного напряжения регулятора скорости;
А
7
– поиск и устранение дефектов тахогенератора;
А
8
– поиск и устранение дефектов ФПЕ;
А
9
– поиск и устранение дефектов РС;
К
7
– контроль Z
9
– выходного напряжения УЗТ;
А
10
– поиск и устранение дефектов УЗТ;
К
8
– контроль Z
10
– выходного напряжения ОГР;
А
11
– поиск и устранение дефектов ОГР;
75
К
9
– контроль Z
11
– выходного напряжения регулятора тока;
А
12
– поиск и устранение дефектов РТ;
К
10
– контроль Z
13
– выходного напряжения нелинейного эле-
мента;
А
13
– поиск и устранение дефектов НЭ;
К
11
– контроль Z
14
– работоспособности УЛ;
А
14
– поиск и устранение дефектов УЛ;
К
12
– контроль Z
15
– работоспособности переключателя харак-
теристик;
А
15
– поиск и устранение дефектов ПХ;
А
16
– поиск и устранение дефектов УО;
А
17
– конец алгоритма.
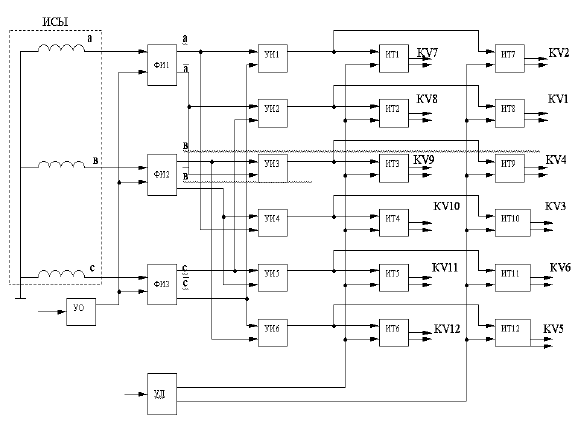
Рис. 2.6. Функциональная схема системы
импульсно-фазового управления электропривода
При поиске множественных дефектов алгоритм применяется
многократно с обязательным промежуточным восстановлением,
т. е. после нахождения одного дефекта процесс поиска останавли-
вается, дефект устраняется, затем проверяется работоспособность
ОД и алгоритм поиска возобновляется, и так до нахождения по-
следнего дефекта.
76
В результате приводим следующую методику разработки ал-
горитма поиска дефектов ЭП с глубиной поиска до функциональ-
ного элемента с применением логической модели:
– на основе анализа работы ЭП, его функциональной схемы
и элементов построить диагностическую модель логического типа;
– построить таблицу состояний ЭП;
– проанализировать таблицу состояний и определить мини-
мальную раз
личающую совокупность контрольных точек;
– упорядочить контрольные точки по степени уменьшения
вероятности возникновения дефекта;
– определить параметры диагностирования и допустимые
пределы их изменения;
– построить алгоритм поиска дефектов на основе результа-
тов проведенного анализа.
Таким образом, приведенная методика использована для ди-
агностирования на первом уровне глубины поиска дефектов.
На следующем у
ровне иерархии рассматривается совокуп-
ность функциональных моделей всех блоков ЭП и поиск дефектов
ведется с глубиной до элемента функциональной схемы блока ЭП.
В качестве примера рассмотрим процедуру разработки алго-
ритма поиска дефектов системы импульсно-фазового управления
данного ЭП. СИФУ формирует сдвоенные прямоугольные им-
пульсы, используемые для управления тиристорами. Фазы им-
пульсов относительно сил
ового напряжения на тиристорах изме-
няются пропорционально напряжению, поступающему на
управляющий орган СИФУ от РТ. Функциональная схема СИФУ
приведена на рис. 2.6 и включает в себя следующие узлы:
– источник синхронизирующего напряжения (ИСН);
– формирователи импульсов (ФИ
1
– ФИ
3
);
– управляющий орган (УО);
– усилители импульсов (УИ
1
– УИ
6
);
– логическое устройство раздельного управления (УЛ);
– импульсные трансформаторы (ИТ
1
– ИТ
12
).
В качестве ИСН используется вторичная обмотка трансформа-
тора
Т
1
питания и синхронизации преобразователя. Каждый ФИ
синхронизирован со своей фазой и формирует импульсы управле-
ния. На усилителях импульсов, кроме усиления по мощности, осу-
ществляется сдваивание импульсов для управления тиристорами.
Для этого на второй вход УИ подаются импульсы с того канала
77
формирователей импульсов, где имеется отставание их на 60 эл.
градусов от импульсов на первом входе УИ. Временная диаграмма
формирования сдвоенных импульсов приведена на рис. 2.7.
Рис. 2.7. Временная диаграмма формирования сдвоенных импульсов
Сдвоенные импульсы с выхода каждого УИ поступают одно-
временно на два ИТ, принадлежащих разным комплектам тиристо-
ров. С другой стороны, подача импульсов на тиристор тем или
иным импульсным трансформатором определяется состоянием
ключей Н и В, которые, в свою очередь, зависят от состояний вы-
ходов УЛ. УЛ предназначено для формирования сигналов управ-
ления кл
ючами Н и В, определяющими нахождение в работе ком-
плекта тиристоров В или Н таким образом, чтобы полностью
исключался режим одновременной работы комплектов.
Для надежного открывания тиристора на его управляющий
электрод необходимо подать импульс определенной полярности,
амплитуды и длительности. Минимально допустимая длитель-
ность управляющего импульса должна быть больше времени
включения тиристора (5
–20мкс). Кроме того, за время действия
импульса ток в анодной цепи тиристора должен успеть нарасти до
тока удержания (10 эл. град. – около 500 мкс).
Крутизна переднего фронта напряжения управляющего им-
пульса должна быть высокой для обеспечения быстрого нараста-
ния тока управления надежного открывания тиристора и умень-
шении потерь при включении.
78
Таблица 2.2
Результаты контроля системы импульсно-фазового управления
Необходимо также обеспечение максимального диапазона
регулирования угла
α (α = 0 – 175 эл. град.), симметрии управ-
ляющих импульсов по фазам, асимметрии противофазных им-
пульсов (не более 0,2 эл. град.), межфазная асимметрия управ-
ляющих импульсов (не более 4 эл. град.), быстродействия. СИФУ
считается работоспособной, если все ее выходные импульсы
в норме и удовлетворяют условию работы с соответствующим ТП.
Для построения диагностической модели используется функ-
циональная схема (рис. 2.6). Кажды
й формирователь импульсов
заменяется двумя блоками в логической модели (ФИ
1
– Q
3
, Q
4
;
ФИ
2
– Q
5
, Q
6
; ФИ
3
– Q
7
, Q
8
), так как для них существуют два вы-
хода(а, а; в, в; c, c). Устройство раздельного управления тоже ха-
рактеризуется двумя блоками в логической модели (
Q
15
, Q
16
), ко-
торые управляют отдельными группами ИТ. Остальные блоки
функциональной схемы заменяются одним блоком логической
79
модели (ИСН –
Q
1
; УО – Q
2
; УИ
1
– УИ
6
– соответственно Q
9
–
Q
14
). Логическая модель СИФУ изображена на рис. 2.6, данные
анализа функциональной схемы СИФУ сведены в таблицу 2.2.
Анализ таблицы показывает, что для поиска дефектов СИФУ
необходимо осуществлять контроль множества выходных сигна-
лов: блоки с
Q
17
по Q
28
. Это множество совпадает с множеством
контрольных точек для проверки работоспособности СИФУ. Та-
ким образом, при контроле выходных сигналов СИФУ имеется
возможность не только определения работоспособности СИФУ,
но и поиска ее дефектов.
Рис. 2.8. Алгоритм поиска дефектов системы
импульсно-фазового управления
Необходимо заметить, что это множество не позволяет разли-
чать неработоспособность блоков
Q
1
и Q
2
(соответственно ИСН
и УО), но, с другой стороны, работоспособность УО определяется
алгоритмом поиска дефектов ЭП до функционального элемента,
дающего возможность сделать заключение о работоспособности
ИСН.
Множество контрольных точек (
К
1
– К
12
), необходимых для
поиска дефектов, показано на рис. 2.6.
Для распознавания дефектов по результатам контроля ис-
пользуются результаты анализа таблицы состояний, которые при-
ведены в таблице 2.2. Цифры 0 означают, что управляющий сиг-
80
нал соответствующего выхода не в норме. Поскольку выходные
сигналы для управления двумя трехфазными группами тиристо-
ров выдаются отдельно, то контроль их осуществляется тоже от-
дельно – сначала для
К
1
– К
6
, а потом для К
7
– К
12
. Причем кон-
троль выходов каждой группы целесообразно производить
одновременно для уменьшения времени контроля, т. к. для поиска
дефектов необходимо осуществлять контроль выходов
К
1
– К
12
.
Учитывая результаты анализа и особенности работы СИФУ,
построим алгоритм поиска дефектов СИФУ с глубиной до функ-
ционального узла, который приведен на рис. 2.7. Алгоритм вклю-
чает операторы:
А
0
– начало алгоритма; А
1
– подготовка СИФУ
и ТСД к диагностированию;
К
1
– контроль первой группы выхо-
дов (
К
1
– К
6
), К
1
= 1, если все выходы в норме; К
1
= 0, если хотя
бы один выход не в норме;
К
2
– контроль второй группы выходов
(
К
7
– К
12
); А
2
– поиск дефектов СИФУ и устранение найденного де-
фекта;
А
3
– конец алгоритма. Для поиска кратных дефектов применя-
ется тот же алгоритм поиска с последующим восстановлением.
Рис. 2.9. Принципиальная схема каскада импульсного усилителя
Таким образом, анализ диагностической модели показывает,
что для поиска дефектов в СИФУ до требуемой глубины необхо-
димо производить контроль только ее выходных импульсов. Если
все выходные импульсы в норме, то СИФУ работоспособна. Если
хотя бы один импульс не в норме, то поиск дефектов в СИФУ
производится по построенному алгоритму.
