Попечителев Е.П. Кореневский Н.А. Электрофизиологическая и фотометрическая медицинская техника: Теория и проектирование
Подождите немного. Документ загружается.

ж
-0 Сброс
+U
J
«•и
t"
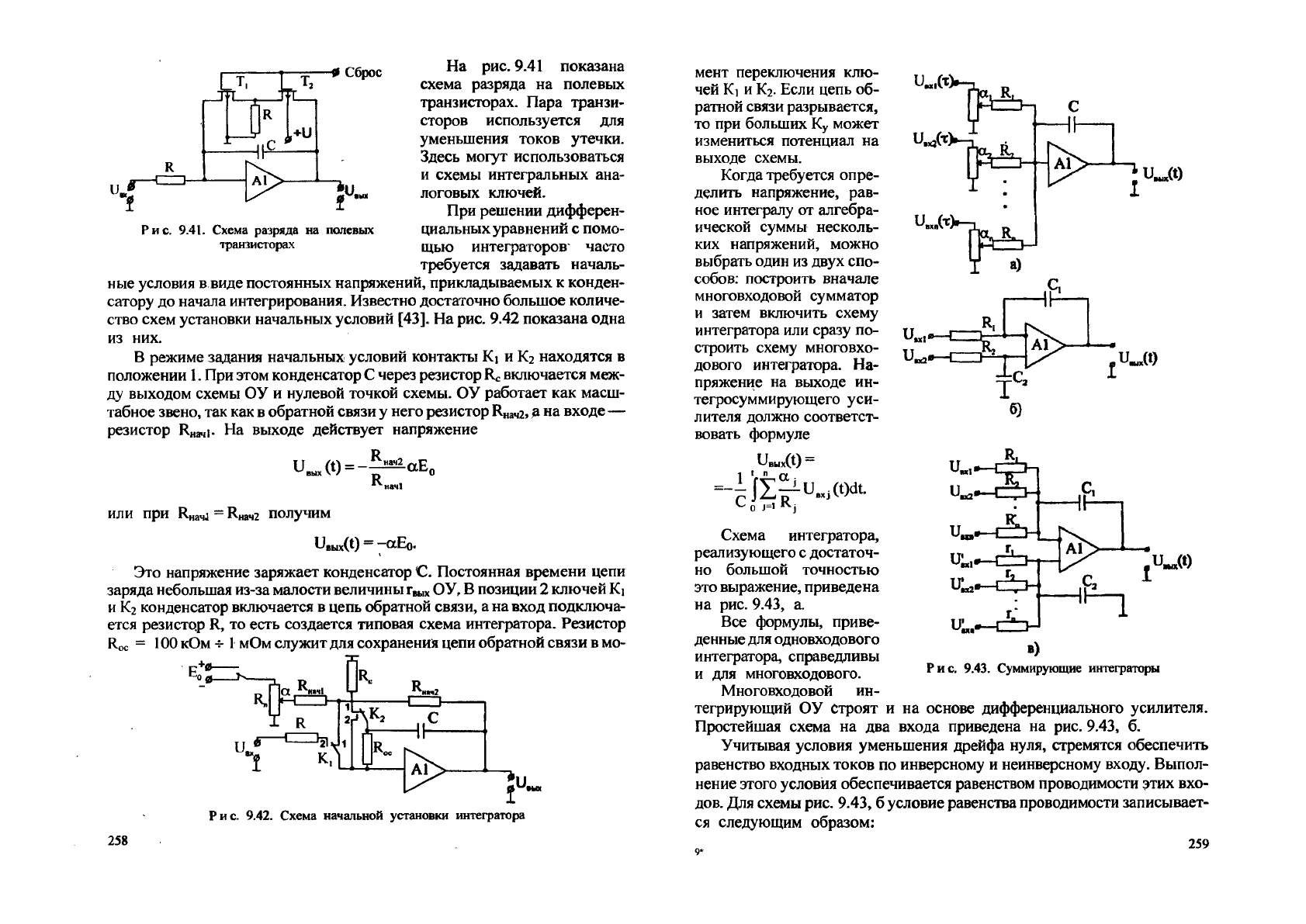
Рис. 9.41. Схема разряда на полевых
транзисторах
На рис. 9.41 показана
схема разряда на полевых
транзисторах. Пара транзи-
сторов используется для
уменьшения токов утечки.
Здесь могут использоваться
и схемы интегральных ана-
логовых ключей.
При решении дифферен-
циальных уравнений с помо-
щью интеграторов часто
требуется задавать началь-
ные условия в виде постоянных напряжений, прикладываемых к конден-
сатору до начала интегрирования. Известно достаточно большое количе-
ство схем установки начальных условий [43]. На рис. 9.42 показана одна
из них.
В режиме задания начальных условий контакты Ki и находятся в
положении
1.
При этом конденсатор
С
через резистор
Rc
включается меж-
ду выходом схемы ОУ и нулевой точкой схемы. ОУ работает как масш-
табное звено, так как в обратной связи у него резистор
R
H
a
4
2>
а на входе—
резистор R
Ha4
i- На выходе действует напряжение
.(t)—
R
-
U.
нач2
аЕ„
ИЛИ при R„
a4
j =
Rh842
получим
и
вых
(1) = -аЕ
0
.
Это напряжение заряжает конденсатор С. Постоянная времени цепи
заряда небольшая из-за малости величины
Гвых
ОУ,
В
позиции 2 ключей Ki
и К
2
конденсатор включается в цепь обратной связи, а на вход подключа-
ется резистор R, то есть создается типовая схема интегратора. Резистор
Roc =
100
кОм
-г-1
мОм служит для сохранения цепи обратной связи в мо-
с
+в
Рис. 9.42. Схема начальной установки интегратора
258
мент переключения клю-
чей Ki и К
2
. Если цепь об-
ратной связи разрывается,
то при больших К
у
может
измениться потенциал на
выходе схемы.
Когда требуется опре-
делить напряжение, рав-
ное интегралу от алгебра-
ической суммы несколь-
ких напряжений, можно
выбрать один из двух спо-
собов: построить вначале
многовходовой сумматор
и затем включить схему
интегратора или сразу по-
строить схему многовхо-
дового интегратора. На-
пряжение на выходе ин-
тегросуммирующего уси-
лителя должно соответст-
вовать формуле
U.
IU*:
с
iu„
I
,<t)
с.
и.
и.
R,
I
с
а
б)
-BMx(t) =
— fl^-u.
С
0 J=
i R
;
j(t)dt.
Рис. 9.43. Суммирующие интеграторы
Схема интегратора,
реализующего с достаточ-
но большой точностью
это выражение, приведена
на рис. 9.43, а.
Все формулы, приве-
денные для одновходового
интегратора, справедливы
и для многовходового.
Многовходовой ин-
тегрирующий ОУ строят и на основе дифференциального усилителя.
Простейшая схема на два входа приведена на рис. 9.43, б.
Учитывая условия уменьшения дрейфа нуля, стремятся обеспечить
равенство входных токов по инверсному и неинверсному входу. Выпол-
нение этого условия обеспечивается равенством проводимости этих вхо-
дов. Для схемы рис. 9.43,
б
условие равенства проводимости записывает-
ся следующим образом:
259

—+ R,= —+ R
2
.
PC, PC
2
При R| = R
2
= R и С) = C
2
= С имеем
U
Bllx
(t) = J-J[U
IK2
(t)-U
B)li
(t)]dt.
КС
о
На рис. 9.43, в показана схема многовходового дифференциального
ОУ для выполнения операций интегрирования. Обычно для этой схемы
выбирают
С]
= С
2
= С, сопротивление резисторов
R,
и п — исходя из тре-
буемых коэффициентов интегрирования
1/RjC
и
1/rjC.
Сумматорные про-
водимости по инверсному и неинверсному входам
i=i j=i
должны быть равны.
Если равенство не выполняется, то к инвертирующему или неинвер-
тирующему входу подключают сопротивление, соединенное с землей с
тем расчетом, чтобы обеспечивалось выполнение равенства g
+
= g~.
9.1.8. Дифференцирующие каскады
Простейшая схема для реализации операции дифференцирования
приведена на рис. 9.44, а.
Для идеального ОУ при равенстве токов i| = i
2
на основании законов
Кирхгофа можно записать
£
~ выхСО
1
а)
U
ux
(T)<*-c=b
| * I.,
MeH^-L
б)
260
Рис. 9.44. Схемы дифференцирующих усилителей
Г
Cd[U
BX
(t) - е
с
(t)]
/ dt = е
с
(t)
-
U
BX
(t)]
/ R;
[e
c
(t) = -U
Bb)X
(t)/K
y
откуда получаем
dlU(t) , U-EXK, +0_
K
dU,
x
(t) (9.25)
dt RC " dt
Проинтегрировав это выражение относительно выходного, получим
IWt) - .
К
у
+1 dt К
у
+1 dt
Учитывая, что при Ку »1, Ку/(Ку +
1)
и 1, можно полагать, что пер-
вый член соответствует операции дифференцирования
U
BHX
(t)*RC^,
dt
а второй член определяет погрешность
AU(t) = -
RC dU
-
(t)
.
К
у
+1 dt
При больших Ку этой составляющей можно пренебречь.
Для определения времени, начиная с которого погрешность в выход-
ном напряжении лежит в заданных пределах, решают дифференциальное
уравнение (9.25).
При К
у
»1 получим
U
Bblx
(t) = -RC^>fi _
e
-.cwc|
dt L J
Абсолютная и относительная погрешности определяются как
AU(t) = U
Bblx0
(t) - U
Bblx
(t) =
.
e
-^
+,)/RC
,
dt
8U(t) =
8U(t)
IWO
Из последнего выражения можно определить, через
какое
время
ti
вы-
ходное напряжение достигнет своего значения с заданной относительной
погрешностью
t, - lnS
Uaon
RC/(K
y
+l).
251

Вывод уравнений погрешности производится аналогично тому, как
это делалось для интегрирующих
ОУ.
Погрешность от разброса парамет-
ров R и С определяется как
AU
RC
(t) = U
BbIx0
(t)(AR/R +ДС/С).
Погрешность от наличия в схеме дополнительного сопротивления
утечки (параллельного емкости С)
AU
y
(t) = -U
BX
(t)^,
погрешность от дрейфа нуля ОУ — по формуле
AUap(t) = RC
•
de
flp
(t)/dt ± е
др
(0,
а погрешность от влияния входных токов — выражением
AU(t) = Ri
BX
(t).
Общую абсолютную статическую погрешность можно определить
как
AU(t) = AU
RC
(t) + AU
y
(t) +
Ufl
P
(t) •
+ AUj(t).
Динамические погрешности дифференцирующего ОУ (как и динами-
ческие погрешности интегрирующего ОУ) можно получить исходя из
анализа передаточных функций и амплитудно-фазочастотных характери-
стик, полученных
из них.
Без учета малых параметров и при малых значе-
ниях постоянной времени ОУ (т
у
«
0)
получим выражение для передаточ-
ной функции
K
0
RCp
RCp+K
0
+1
Амплитудно-фазочастотная характеристика при р = jco имеет вид
w
(ico)
=
K
°
R2CV
+ j K
0
(K
0+
l)RCco
" (K
0
+1) + R
2
CV
J
(K
0
+1) + R
2
CV
откуда ее амплитудно-частотная характеристика определяется выраже-
нием
А(ю) = К
0
RCto/-y/(K
0
+1)
2
+R
2
CV,
а фазочастотная характеристика — выражением
262
Ф(со) = arctg
ЯСю
Погрешность в передаточной функции определяется как разность ее
идеального и реального выражений
K
0
pRC pRC+1
AW (p) = pRC ^ = RCp
д
K
0
+1 +pRC . K
0
+l + pRC
Погрешность амплитудно-фазочастотной характеристики
>
2/^2„2 /v . ,
ч
i т>
AW Г K
0
R С to . (K
0
+
1)
+ R С to
"°
ffl)
(K
0
+1)
2
+R
2
C
2
co
2
V
0
+1)
2
+R
2
C
2
CO
2
Фазовые искажения выходного напряжения
в
зависимости от частоты
определяются с помощью выражения
Аср(ю)
= arctg[-l/(RCco) - l/(KoRCco) - RCco/K
0
].
Абсолютная амплитудная погрешность при Ко »1
АА(со) =
2
VR
2
CV(Kg+R
2
C
2
co)
+
Kg.
K
0
R
2
CV
v
Из последнего выражения следует, что амплитуда сигнала растет с
ростом частоты, что говорит о высокой чувствительности схемы к высо-
кочастотным помехам. Это создает ограничения к практическому испо-
льзованию таких
схем.
Для уменьшения влияния шумов
и
улучшения ста-
бильности схемы последовательно с конденсатором включают неболь-
шой резистор (рис. 9.44, б). Передаточная функция такой схемы имеет
вид
W(p) = -г,Р/(т
2
Р +
1)
= и
вых
(р)/и
вх
(р),
где Ti =
RoC;
т
2
= RiC.
Для этой схемы справедливо выражение
п
-
т
u
-x(t)
+ T
dU
Bblx
(t)
-UBWX - ti + Т
2
.
dt dt
Второй член в этом уравнении — погрешность преобразования
dU
BMX
(t)
AU(t) = т
2
-
dt
Погрешность уменьшается с уменьшением т
2
. В реальных схемах
ищут компромисс между точностью дифференцирования и уровнем по-
мех.
263
9.2. УСТРОЙСТВА ФИЛЬТРАЦИИ СИГНАЛОВ
Фильтры предназначены для того, чтобы йз всех подаваемых на его
вход сигналов пропускать на выход сигналы определенных, наперед за-
данных частот.
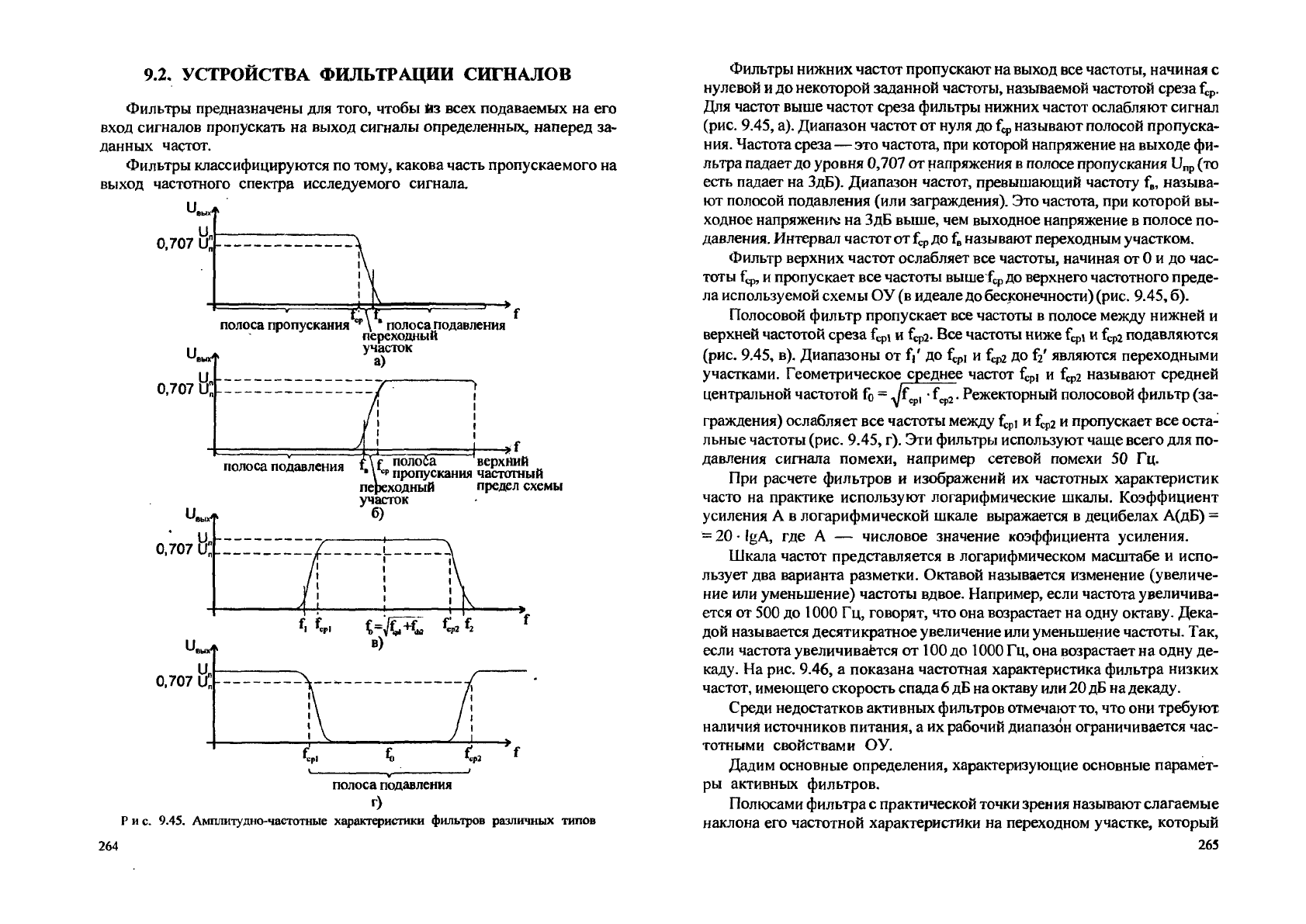
Фильтры классифицируются по тому, какова часть пропускаемого на
выход частотного спектра исследуемого сигнала
и„
0.707 1Я
полоса пропускания
р
\
полоса подавления
переходный
участок
а)
полоса подавления
. , *f
полоса верхний
-
р
пропускания частотный
:ходный предел схемы
участок
б)
0,707 Н"
0,707 И:
полоса подавления
г)
Рис. 9.45. Амплитудно-частотные характеристики фильтров различных типов
258
Фильтры нижних частот пропускают
на
выход все частоты, начиная с
нулевой
и
до некоторой заданной частоты, называемой частотой среза
f
cp
.
Для частот выше частот среза фильтры нижних частот ослабляют сигнал
(рис. 9.45, а). Диапазон частот от нуля до
f
cp
называют полосой пропуска-
ния. Частота среза—это частота, при которой напряжение на выходе фи-
льтра падает до уровня 0,707 от напряжения в полосе пропускания U
np
(то
есть падает на ЗдБ). Диапазон частот, превышающий частоту
f„,
называ-
ют полосой подавления (или заграждения). Это частота, при которой вы-
ходное напряженна на ЗдБ выше, чем выходное напряжение в полосе по-
давления. Интервал частот от fq, до
f
B
называют переходным участком.
Фильтр верхних частот ослабляет все частоты, начиная от 0 и до час-
тоты
fq,,
и пропускает все частоты выше
f
cp
до
верхнего частотного преде-
ла используемой схемы ОУ
(в
идеале
до
бесконечности)
(рис.
9.45, б).
Полосовой фильтр пропускает все частоты в полосе между нижней и
верхней частотой среза
f
cp
i
и
fcp
2
-
Все частоты ниже
f
cp
i
и
f
cp
2
подавляются
(рис. 9.45, в). Диапазоны от f|' до f
cpl
и
f
cp
2
до f
2
' являются переходными
участками. Геометрическое среднее частот f^ и f
cp
2 называют средней
центральной частотой
fo
= ^f
cpl
-f
cp2
.
Режекторный полосовой фильтр (за-
граждения) ослабляет все частоты между
f
cp
i
и
f
cp2
и пропускает все оста-
льные частоты (рис. 9.45, г). Эти фильтры используют чаще всего для по-
давления сигнала помехи, например сетевой помехи 50 Гц.
При расчете фильтров и изображений их частотных характеристик
часто на практике используют логарифмические шкалы. Коэффициент
усиления А в логарифмической шкале выражается в децибелах А(дБ) =
- 20
•
IgA, где А — числовое значение коэффициента усиления.
Шкала частот представляется в логарифмическом масштабе и испо-
льзует два варианта разметки. Октавой называется изменение (увеличе-
ние или уменьшение) частоты вдвое. Например, если частота увеличива-
ется от 500 до 1000 Гц, говорят, что она возрастает на одну октаву. Дека-
дой называется десятикратное увеличение или уменьшение частоты. Так,
если частота увеличивается от
100
до
1000 Гц,
она возрастает на одну де-
каду. На рис. 9.46, а показана частотная характеристика фильтра низких
частот, имеющего скорость спада
6 дБ
на октаву
или 20 дБ
на декаду.
Среди недостатков активных фильтров отмечают
то,
что они требуют
наличия источников питания, а их рабочий диапазон ограничивается час-
тотными свойствами ОУ.
Дадим основные определения, характеризующие основные парамет-
ры активных фильтров.
Полюсами фильтра
с
практической точки зрения называют слагаемые
наклона его частотной характеристики на переходном участке, который
265
обусловлен наличием RC-
цепей, используемых для
формирования частотных
характеристик.
Порядок фильтра — это
число его полюсов. Каждый
полюс вносит в наклон пе-
реходного участка 6 дБ на
октаву или 20 дБ на декаду.
Число полюсов фильтра
связывают также со степе-
нью полиномов передаточ-
ных функций фильтров.
Коэффициент затухания
а определяет форму харак-
теристики фильтра на пере-
ходном участке и вид вы-
броса характеристики в по-
лосе пропускания вблизи
переходного процесса. Та-
ким образом, коэффициент
затухания определяет фор-
му частотной характеристи-
ки фильтра, то есть его тип.
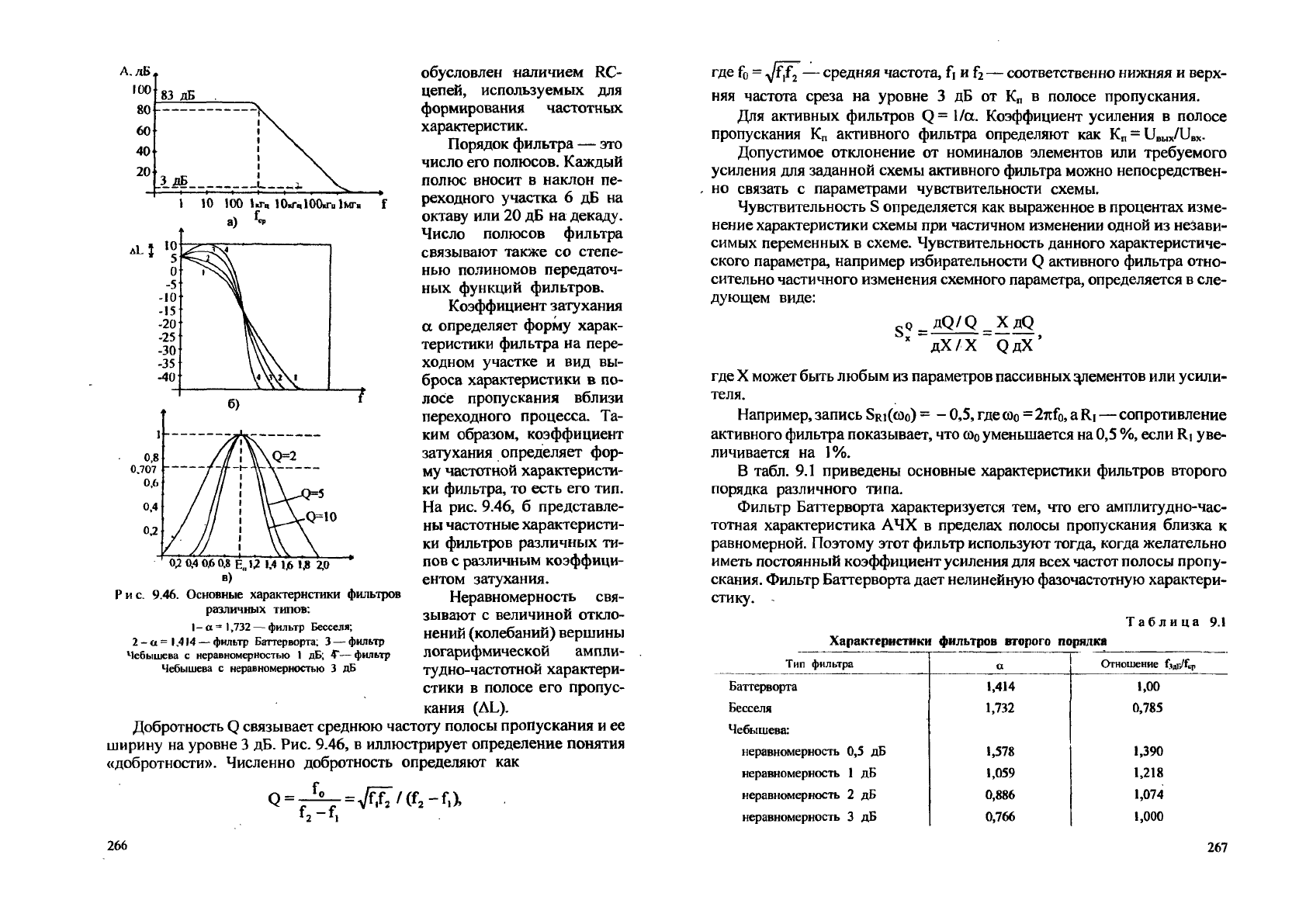
На рис. 9.46, б представле-
ны частотные характеристи-
ки фильтров различных ти-
пов с различным коэффици-
ентом затухания.
Неравномерность свя-
зывают с величиной откло-
нений (колебаний) вершины
логарифмической ампли-
тудно-частотной характери-
стики в полосе его пропус-
кания (AL).
Добротность Q связывает среднюю частоту полосы пропускания и ее
ширину на уровне 3 дБ. Рис. 9.46, в иллюстрирует определение понятия
«добротности». Численно добротность определяют как
02
0,4 0.6 0.8 F
n
\2
1,4
If, Ifi 2,0
В)
Рис. 9.46. Основные характеристики фильтров
различных типов:
I
- а
=»
1,732 — фильтр Бесселя;
2 - а = 1,414 — фильтр Батгерворта; 3 — фильтр
Чебышева с неравномерностью 1 дБ; 4"—фильтр
Чебышева с неравномерностью 3 дБ
Q-
f
°
f
2
-f,
=Vf^/(f
2
-f,),
258 266
где
f
0
= -Jff
2
— средняя частота,
fj
и
f
2
— соответственно нижняя и верх-
няя частота среза на уровне 3 дБ от К„ в полосе пропускания.
Для активных фильтров Q = 1/а. Коэффициент усиления в полосе
пропускания К
п
активного фильтра определяют как К
п
= и
вых
/и
вх
.
Допустимое отклонение от номиналов элементов или требуемого
усиления для заданной схемы активного фильтра можно непосредствен-
но связать с параметрами чувствительности схемы.
Чувствительность S определяется как выраженное в процентах изме-
нение характеристики схемы при частичном изменении одной из незави-
симых переменных в схеме. Чувствительность данного характеристиче-
ского параметра, например избирательности Q активного фильтра отно-
сительно частичного изменения схемного параметра, определяется в сле-
дующем виде:
pQ/Q XRQ
х
дХ/Х Q дХ'
где
X
может быть любым из параметров пассивных элементов или усили-
теля.
Например, запись SRJ(G>O) = - 0,5, где ЮО = 27TFO, A RI—сопротивление
активного фильтра показывает, что
too
уменьшается на
0,5
%, если R| уве-
личивается на 1%.
В табл. 9.1 приведены основные характеристики фильтров второго
порядка различного типа.
Фильтр Батгерворта характеризуется тем, что его амплитудно-час-
тотная характеристика АЧХ в пределах полосы пропускания близка к
равномерной. Поэтому этот фильтр используют тогда, когда желательно
иметь постоянный коэффициент усиления для всех частот полосы пропу-
скания. Фильтр Батгерворта дает нелинейную фазочастотную характери-
стику.
Таблица 9.1
Характеристики фильтров второго порядка
Тип фильтра
а
Отношение ОдгЛф
Батгерворта 1,414 1,00
Бесселя
1,732
0,785
Чебышева:
неравномерность 0,5 дБ
1,578
1,390
неравномерность 1 дБ
1,059
1,218
неравномерность 2 дБ
0,886
1,074
неравномерность 3 дБ
0,766
1,000

Характеристика фильтра Чебышева имеет волнообразные зубцы в по-
лосе пропускания и равномерна
в
полосе подавления. Количество зубцов
в таких фильтрах тем больше, чем больше его порядок. Амплитуда этих
зубцов может
быть
задана
в
процессе проектирования. Фильтр Чебышева
обеспечивает на переходном участке крутые характеристики. Фазоча-
стотная характеристика фильтра Чебышева еще более нелинейна, чем у
фильтра Баттерворта. Наклон характеристики у фильтра Чебышева мо-
жет превышать 6 дБ на октаву на один полюс. Зависимость ослабления в
децибелах на переходном участке для этого фильтра от частоты имеет
вид
OS = 20IgE + 6(n - 1) + 20nlg(co/co
C
p),
где
n
— порядок фильтра, ю
ср
=
27tf
cp
,
Е—постоянная, принимающая зна-
чение от 0 до
1
и характеризующая неравномерность характеристики в
полосе пропускания.
Фильтры Бесселя обладают линейной фазовой характеристикой. Эти
фильтры
в
отличие от фильтров Баттерворта
и
Чебышева практически не
дают выбросов при подаче на вход ступенчатых сигналов, поэтому их
применяют
для
фильтрации прямоугольных импульсов без изменения их
формы. Фильтры Бесселя дают наклон меньший 6 дБ на октаву. Частота
среза фильтра Бесселя определяется как частота, на которой запаздыва-
ние по фазе © равно половине запаздывания, максимально возможной
для данного фильтра
©(fcp)
=
©max/2
= (птс/2)/2рад,
где © — запаздывание по фазе.
9.2.1.Типовые схемы активных фильтров
Схема одного из популярных фильтров Саплена
и
Кея нижних частот
второго порядка представлена на рис. 9.47, а.
Каждая из
RC
цепей вносит наклон
6
дБ на октаву на переходном уча-
стке. Сопротивления R
A
и
R
B
определяют коэффициент затухания. Харак-
теристика вблизи края полосы пропускания формируется за счет обрат-
ной связи через конденсатор С]. Есди R, = R
2
и Ci = С
2
, то методика рас-
чета фильтра достаточна проста.
Расчет фильтра начинается с выбора его типа и определения величи-
ны f
cp
.
1. Из табл. 9.1 для выбранного типа фильтра выбираем отношение
f;Wfc
P
= d и определяем величину
f
cp
= f3
fl
g/d.
268
2. Выбираем величину
С = Ci =
С
2
и
рассчитываем ве-
личину R из соотношения
f
cp
= l/(27tRC), R = R, = R
2
.
Возможно, пп.1 и 2 при-
дется повторить, чтобы вели-
чина
R
лежала
в
разумных пре-
делах.
3. Из табл. 9.1 находим ве-
личину коэффициента затуха-
ния.
4. Выбираем подходящее
значение RA, которое удобно
выбирать равным
R, и
находим
величину
Rb
= (2 - a)R
A
.
5. Находим коэффициент
усиления в полосе пропуска-
ния по формуле K„ = RB/RA + 1.
Схема фильтра верхних частот Саллена—Кея
с
равными компонента-
ми приведена на рис. 9.47, б. Каждая из RC цепей вносит наклон по 6 дБ
на октаву. Характеристика вблизи края полосы пропускания формирует-
ся за счет обратной Связи через сопротивление R|. При расчете парамет-
ров фильтра, как
и
для фильтра нижних
частот,
с помощью
табл. 9.1
нахо-
дится величина
f
cp
=
f
3
дБ/d.
Полагая, что С = Ci = С
2
и R =
Rj
= R
2
, выби-
раем величину С и из соотношения f
cp
= l/(27tRC). Из табл. 9.1 находим
величину а, соответствующую выбранному типу фильтра.
Задавая величину R
A
, находим R
B
,
RB
=
(2
— a)R
A
.
По формуле K
n
= Rb/Ra +
1
находим коэффициент усиления в полосе
пропускания.
Оба фильтра (верхних и нижних частот) Саллена и Кея настраивают
следующим образом.
1. Величина
f
cp
устанавливается совместным изменением Q и С
2
и Ri
и R
2
.
2. Величина а устанавливается изменением Rb.
Схема простого и хорошо работающего полосового фильтра с уме-
ренными добротностями (имеет Q порядка 10) приведена на рис 9.48, а.
В ней часть характеристики, соответствующая фильтру низких частот,
обеспечивается элементами R
b
С
ь
а часть характеристики, соответству-
ющая фильтру верхних
частот,
обеспечивается элементами R
2
,
С
2
.
Парал-
1
лельное включениеR3,
С]
в цепи обратной связи обеспечивает положение
максимума АЧХ вблизи частоты f
0
. Сопротивление R
2
не обязательный
269
и
LC,
R*
4
?г
"Т
а)
Re
U.
б)
0*
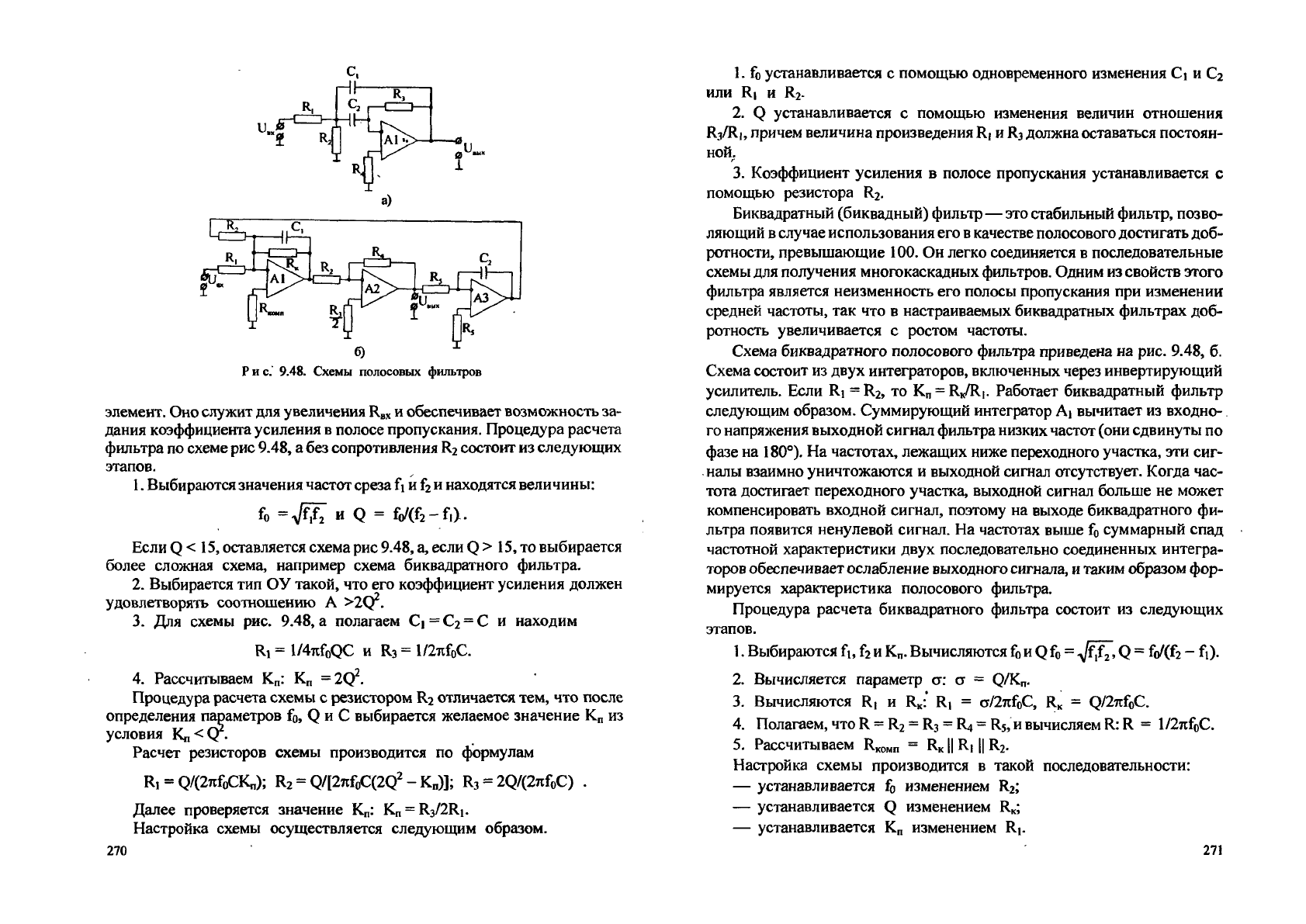
Рис. 9.47. Фильтры Саллена и Кея низких
(а) и верхних (б) частот
С,
элемент. Оно служит для увеличения
R
BX
и обеспечивает возможность за-
дания коэффициента усиления в полосе пропускания. Процедура расчета
фильтра по схеме рис 9.48, а без сопротивления R
2
состоит из следующих
этапов.
1.
Выбираются значения частот среза
f\
и
f
2
и находятся величины:
fo и Q = fo/(f
2
-f.>.
Если Q <
15,
оставляется схема рис 9.48, а, если Q > 15, то выбирается
более сложная схема, например схема биквадратного фильтра.
2. Выбирается тип ОУ такой, что его коэффициент усиления должен
удовлетворять соотношению A >2Q
2
.
3. Для схемы рис. 9.48, а полагаем Ci = С
2
= С и находим
Ri = l/4Ttf
0
QC и R
3
= l/2nf
0
C.
4. Рассчитываем К
п
: К
п
=2Q
2
.
Процедура расчета схемы с резистором R
2
отличается тем, что после
определения параметров fo, Q и С выбирается желаемое значение К
п
из
условия Kn<v.
Расчет резисторов схемы производится по формулам
R, = Q/(27tfoCK„); R
2
= Q/[2nf
0
C(2Q
2
- К
п
)]; R
3
= 2Q/(27if
0
C) .
Далее проверяется значение К
п
: K„ = R3/2Ri.
Настройка схемы осуществляется следующим образом.
258 270
1.
fo
устанавливается с помощью одновременного изменения С] и С
2
или R| и R
2
.
2. Q устанавливается с помощью изменения величин отношения
R3/R1,
причем величина произведения R
(
и
R
3
должна оставаться постоян-
ной.
3. Коэффициент усиления в полосе пропускания устанавливается с
помощью резистора R
2
.
Биквадратный (биквадный) фильтр —
это
стабильный фильтр, позво-
ляющий в случае использования его
в
качестве полосового достигать доб-
ротности, превышающие 100. Он легко соединяется в последовательные
схемы для получения многокаскадных фильтров. Одним
из
свойств этого
фильтра является неизменность его полосы пропускания при изменении
средней частоты, так что в настраиваемых биквадратных фильтрах доб-
ротность увеличивается с ростом частоты.
Схема биквадратного полосового фильтра приведена на рис. 9.48, б.
Схема состоит из двух интеграторов, включенных через инвертирующий
усилитель. Если Ri =R
2
, то K
n
= R,c/R|. Работает биквадратный фильтр
следующим образом. Суммирующий интегратор А] вычитает из входно-
го напряжения выходной сигнал фильтра низких частот (они сдвинуты по
фазе на 180°). На частотах, лежащих ниже переходного участка, эти сиг-
налы взаимно уничтожаются и выходной сигнал отсутствует. Когда час-
тота достигает переходного участка, выходной сигнал больше не может
компенсировать входной сигнал, поэтому на выходе биквадратного фи-
льтра появится ненулевой сигнал. На частотах выше f
0
суммарный спад
частотной характеристики двух последовательно соединенных интегра-
торов обеспечивает ослабление выходного сигнала, и таким образом фор-
мируется характеристика полосового фильтра.
Процедура расчета биквадратного фильтра состоит из следующих
этапов.
1.
Выбираются
fj, f
2
и К
п
. Вычисляются
f
0
и
Q
f
0
=
д/f,f
2
,
Q =
fo/(f
2
- fi).
2. Вычисляется параметр сг: ст = Q/К
п
.
3. Вычисляются R| и R
K
: R| = cr/27tfoC, R
K
= Q/27if
0
C.
4. Полагаем, что R = R
2
= R
3
= R) =
R
5
,
и вычисляем
R:
R = l/27tf
0
C.
5. Рассчитываем R
K0Mn
= R
K
|| Ri || R
2
-
Настройка схемы производится в такой последовательности:
— устанавливается 1J) изменением R
2
;
— устанавливается Q изменением R
K
;
— устанавливается К
п
изменением Rj.
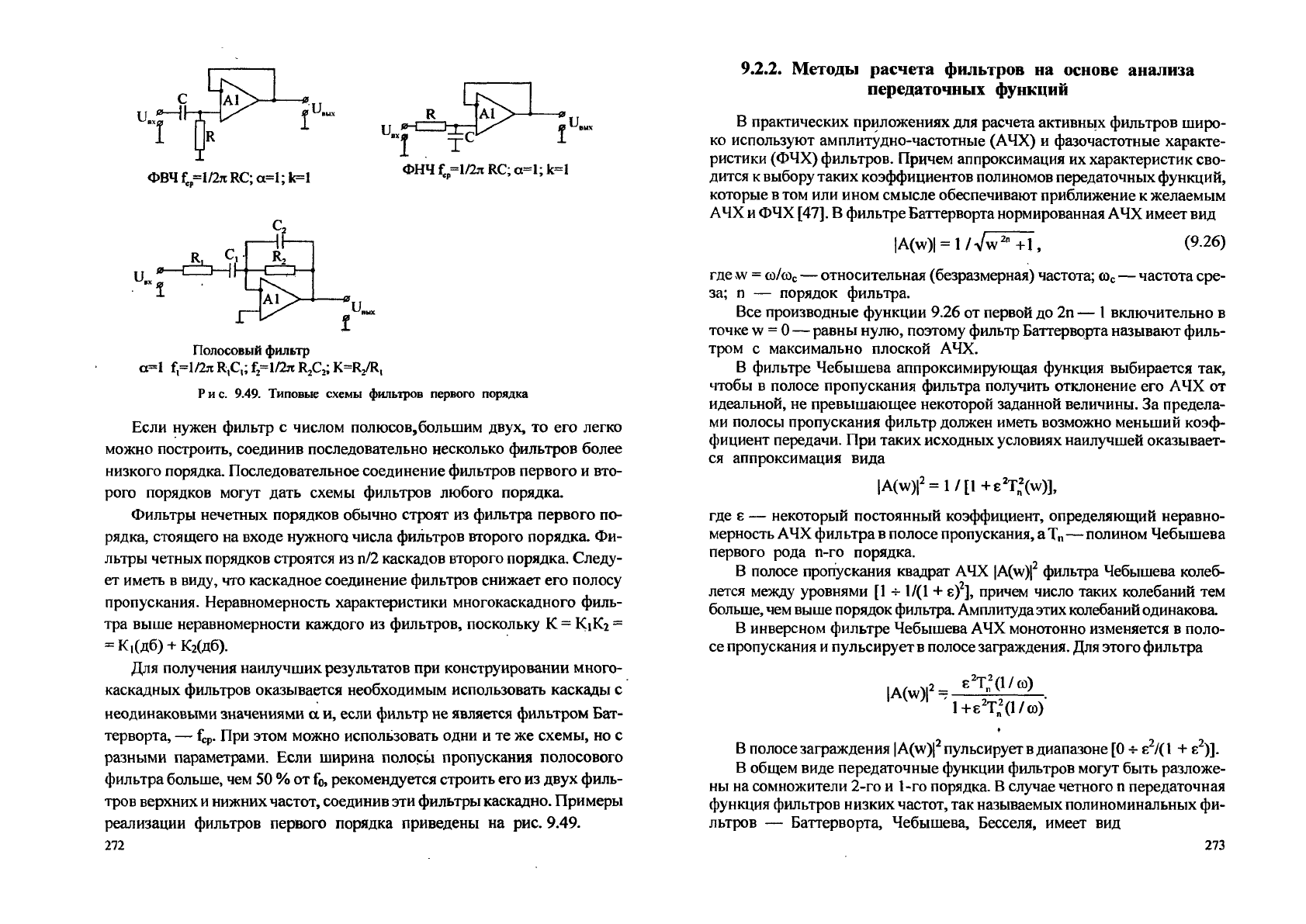
I
ФВЧ f
c
=l/2n: RC; а=1; к=1
ФНЧ f
c(
,=l/2;i RC; а=1; к=1
Полосовый фильтр
а=1 f=l/2;i R,C,; f
2
=l/2n R,C,; K=R/R,
Рис. 9.49. Типовые схемы фильтров первого порядка
Если нужен фильтр с числом полюсов,большим двух, то его легко
можно построить, соединив последовательно несколько фильтров более
низкого порядка. Последовательное соединение фильтров первого и вто-
рого порядков могут дать схемы фильтров любого порядка.
Фильтры нечетных порядков обычно строят из фильтра первого по-
рядка, стоящего на входе нужного числа фильтров второго порядка. Фи-
льтры четных порядков строятся из п/2 каскадов второго порядка. Следу-
ет иметь в виду, что каскадное соединение фильтров снижает его полосу
пропускания. Неравномерность характеристики многокаскадного филь-
тра выше неравномерности каждого из фильтров, поскольку К = KiK
2
=
= К,(дб) + К
2
(дб).
Для получения наилучших результатов при конструировании много-
каскадных фильтров оказывается необходимым использовать каскады с
неодинаковыми значениями а и, если фильтр не является фильтром Бат-
терворта, —
f
cp
.
При этом можно использовать одни и те же схемы, но с
разными параметрами. Если ширина полосы пропускания полосового
фильтра больше, чем 50 % от
fo,
рекомендуется строить его из двух филь-
тров верхних
и
нижних частот, соединив
эти
фильтры каскадно. Примеры
реализации фильтров первого порядка приведены на рис. 9.49.
272
9.2.2. Методы расчета фильтров на основе анализа
передаточных функций
В практических приложениях для расчета активных фильтров широ-
ко используют амплитудно-частотные (АЧХ) и фазочастотные характе-
ристики (ФЧХ) фильтров. Причем аппроксимация их характеристик сво-
дится
к
выбору таких коэффициентов полиномов передаточных функций,
которые в том или ином смысле обеспечивают приближение к желаемым
АЧХ
и
ФЧХ [47]. В фильтре Баттерворта нормированная АЧХ имеет вид
|A(w)| = l/Vw
2n
+l, (9-26)
где
w =
to/to
c
— относительная (безразмерная) частота;
ш
с
— частота сре-
за; п — порядок фильтра.
Все производные функции 9.26 от первой до 2п —
1
включительно в
точке w =
0
— равны нулю, поэтому фильтр Баттерворта называют филь-
тром с максимально плоской АЧХ.
В фильтре Чебышева аппроксимирующая функция выбирается так,
чтобы в полосе пропускания фильтра получить отклонение его АЧХ от
идеальной, не превышающее некоторой заданной величины. За предела-
ми полосы пропускания фильтр должен иметь возможно меньший коэф-
фициент передачи. При таких исходных условиях наилучшей оказывает-
ся аппроксимация вида
|A(w)|
2
=l/[l+e
2
T
2
(w)],
где е — некоторый постоянный коэффициент, определяющий неравно-
мерность АЧХ фильтра в полосе пропускания, а Т
п
—полином Чебышева
первого рода п-го порядка.
В полосе пропускания квадрат АЧХ |A(w)|
2
фильтра Чебышева колеб-
лется между уровнями [1 -ь 1/(1 + е)
2
], причем число таких колебаний тем
больше, чем
выше порядок
фильтра.
Амплитуда
этих
колебаний одинакова.
В инверсном фильтре Чебышева АЧХ монотонно изменяется в поло-
се пропускания
и
пульсирует в полосе
заграждения.
Для этого фильтра
|A(w)|
2
=
-
1+в
2
Т
2
(1/со)
•
В
полосе заграждения |A(w)|
2
пульсирует
в
диапазоне [0
4- е
2
/(1
+ е
2
)].
В общем виде передаточные функции фильтров могут быть разложе-
ны на сомножители 2-го и
1-го
порядка. В случае четного п передаточная
функция фильтров низких частот, так называемых полиноминальных фи-
льтров — Баттерворта, Чебышева, Бесселя, имеет вид
273

n/2
W(p)=n
cxo.
w p
z
+
рЬ
(
со
с
+C&
(9.27)
Инверсный фильтр Чебышева и эллиптический фильтр, которые от-
носят к нейолиноминальным фильтрам для фильтров нижних частот,
имеют передаточные функции вида
. wao-fl^-ffo'?.
н Р +
pbjCO,
+с
;
со
с
(9.28)
В работах [16,47] приводятся таблицы коэффициентов a,
bj с*
для раз-
личных фильтров различных порядков. В табл. 9.2 даны коэффициенты
для наиболее распространенных практических схем.
Таблица 9.2
Таблица расчетных коэффициентов
Порядок фильтра
2
4
б
номер звена 1 1 2
1
2 3
Фильтр b
1,4142
0,7654
1,8478 0,5176 1.4142 1,9319
Батгерворта
с
1,0000 1,0000
1,0000
1,0000 1,0000 1,0000
Фильтр b 1,4256 0,3507
0,8467
0,1553 0,1243
0,5796
Чебышева q
t
—
0,5 дБ
с
1,5162 1,0635
0,3564
1,0230 0,5900
0,1570
Фильтр
ь
1,0977 0,2791
0,6737
0,1244
0,3398 0,4641
Чебышева qi =
1
дБ с 1,1025
0,9865 0,2794 0,9907 0,5577 0,1247
Фильтр
b
0,8038 0,2098
0,5064
0,0939 0,2567 0,3506
Чебышева qi = 2 дБ
с
0,8231
0,9287 0,2216 0,9660 0,5329
0,0999
Инверсный а 100,99
4,7485 27,676
2,1487
4,0094 29,927
Фильтр Чебышева
q2
= -40 дБ b
1,4141
0,6892
2,0315 0,3791 1,3338
2,5582
с
1,5214 0,4478
1,0514
0,3176 0,7965
1,0142
Эллиптический фильтр
а
65,875
2,2207 10,214
1,5696 7,6393
1,1786
qi = 2 дБ
b 0,7987
0,5545
0,1518
0,4905
0,1704 0,0317
q
2
= -40 дБ
с
0,8293
0,2991 0,9598
0,2315
0,7759
0,9905
Фильтр Бесселя а
3,0000 5,7924
4,2076
5,0319
8,4967
7,4714
b
3,0000' 9,1401 11,488 26,514 18,801 20,853
• В таблице Обозначены: qi — уровень минимумов пульсации АЧХ в
полосе пропускания (уровень максимумов принят за 0 дБ); q
2
— уровень
максимумов пульсации АЧХ в полосе заграждения (между этими макси-
мумами АЧХ спадает до нуля). Уровень - 40 дБ соответствует
1
%. Коэф-
фициенты
aj bj
q, приведенные в табл. 9.2, рассчитаны так, что на частоте
Юср
АЧХ фильтров Батгерворта и инверсного фильтра Чебышева имеют
спад около -
3
дБ (уменьшаются до уровня 1/
л/2).
Для фильтров Чебыше-
274
ва и эллиптического фильтра АЧХ в полосе пропускания пульсируют
между уровнями 1/(10
ч1/2
°) и 1.
Для фильтра типа Саллена—Кея (см. рис. 9.47, а) передаточная функ-
ция имеет вид
W(p)
=
1
+ R
B
/R
A
1
+pC
2
(R, +R
2
)-pC,R,R
B
/R
a
+p
2
C,C
2
R
I
R
2
(9
'
29)
Для фильтра, изображенного на рис. 9.50 и называемого структурой
Рауха,
W(p)
=
R
2
/ R,
1
+ pC
2
(R
2
+ R
3
+R
2
R
3
/R^ + p^CjRjRj
(9.30)
Если сравнивать выражения (9.29) и (9.30) с выражениями (9.27) и
(9.28), можно сделать вывод о том, что схемы, представленные на
рис. 9.47, а и 9.50, пригодны лишь для реализации полиноминальных фи-
льтров (Батгерворта, Чебышева и Бесселя).
Более универсальным фильтром является биквадратный фильтр,
один из вариантов схемы которого приведен на рис. 9.51. Для этой схемы
W,(p) =
R< _ R*R
A
[ R,
- + pC
2
5 6
I
2
R
8
R
2
(^R, R
7
R, l_„2
rr
R
3
R
5
R
6
P J 2
U—FR», R
8
' '
R
2
L
R
, R
7
J • ' '
R
7
U
BX
(p) l + pC
2
R
3
R
5
R
6
/(R
2
R
4
) + p
2
C,C
2
R3
R
5
R
6 /
R
,
;(9.31)
R
6
R
3
[
R
6
R
5
R
6
w
2
(p)
=
(1
+ pC,R
2
)
U.b,
2
(P)_
R
l
R
2
V
R
7
R
4
R
8 /
U
BX
(p)
1
+ pC
2
R
3
R
5
R
6
/ (R
2
R
4
) + p
2
C,C
2
R
3
R
5
R
6 /
R
<
. (9.32)
Если принять
R1R3
= R
2
R
7
,
TO ДЛЯ
(9.31) в качестве
U
BblX
]
можно испо-
льзовать выходное напряжение звена эллиптического фильтра или инвер-
сного фильтра Чебышева. Если же
R7
=
Rg
=
°о,
то
для
(9.32)
U
Bb]x2
соответ-
ствует звену второго порядка.
Биквадратный фильтр менее
чувствителен к неточности элемен-
тов и проще
в
настройке. Сопостав-
ляя формулы (9.29)—(9.32) с фор- R,
мулами (9.27) и (9.28), нетрудно Ц
вывести формулы для расчета со-
противлений и емкостей звеньев
второго порядка.
•ч
0-С
К
Т
г1
А1
Рис. 9.50. Фильтр со структурой Рауха
275

Исходными данными являются частота среза фильтра f
c
= со
с
/(2и) и
коэффициент усиления звена в полосе пропускания —
А.
Расчет начина-
ется с выбора емкости Сь причем рекомендуется Ci » 10/f
c
(мкФ), где f
c
— частота среза в герцах.
Для схемы рис. 9.47, а определяются С
2
, Ri и R
2
(значения а, Ь, с бе-
рутся из табл. 2.2):
С
2
< [А -
1
+ b
2
/(4c)]Cj;
R, =
l/(7tf
c
C,)-y/[b
+ >
2
+ 4с(А-1)-4сС
2
/С,];
R
2
= l/[cC,C
2
R,(27rf
c
)
2
].
Если А = 1, то R
A
=
оо;
R
D
= 0; если А > 1, то R
A
= A(R, + R
2
)/(A - 1);
R
B
= A(R| + R
2
).
Для схемы, изображенной на рис 9.50, порядок расчета иной:
1. C,*10/f
c
;
2. С
2
< b
2
C|/[4c(|A| + 1)];
3. R
2
= (|А| +
l)/(7tf
c
C,)/Ib
+
Л
/Ь
2
-
4с(|
А|+1)С
2
/С,];
4. R, = R
2
/|A|;
5. R
3
= l/[cC,C
2
(27tf
c
)
2
R
2
].
Для биквадратного полиноминального фильтра (см.рис. 9.51) с вы-
ходным напряжением U
Bblx2
: R
7
=
со;
Rj =
oo;
С| = 10/Т
с
(мкФ); С
2
= Сь
R, = l/(27tf
c
C,); R, = R, = R
5
; R, = R4/(Ac); R
2
= R,/b; R
6
= R4/C.
Для биквадратного полиноминального фильтра с выходным напряже-
нием и
вых1
:
С, = 10/fc; С
2
= С,; R, =
a/(Abc27tf
c
C,);
R
2
= l/(b27tf
c
C,); R, = R
3
;
R
3
= l/27tf
c
C,; Rj = CjRa/C; Re = l/(27tf
c
CrTc); R
7
= aRa/(Ac);
Rs = l/(A27tf
c
C
2
-s/c).
276
Передаточные функции фильтров верхних частот ФВЧ можно полу-
чить, воспользовавшись выражениями (9.27)
и
(9.28), если произвести за-
мену р на
со
2
/ р. Для неполиноминальных ФВЧ характер передаточной
функции сохраняется, изменяются лишь ее коэффициенты. Таким обра-
зом, можно пользоваться теми же схемами, но с другими сопротивления-
ми и емкостями.
Для полиноминальных ФВЧ меняется характер Передаточных функ-
ций. Во всех случаях параметры ФВЧ могут быть рассчитаны по данным
табл 9.2 на заданной частоте среза
f
c
= со
с
/(2тс).
9.2.3. Подавление помех активными фильтрами
Эффективным способом подавления продольных
помех,
как
было
по-
казано выше, является применение дифференциальных схем подавления
синфазных помех и применение гальванических развязок. Одним из эф-
фективных способов подавления дифференциальных помех, если спект-
ры мощности помех и сигналов не совпадают, является фильтрация сиг-
налов.
Для оценки степени «засоренности» полезного сигнала помехами ис-
пользуют известное отношение «сигнал —
шум»
(С/Ш)—Ч^ых. Через это
отношение удобно, например, выразить степень улучшения качества сиг-
нала дифференциальным усилителем с высоким коэффициентом ослаб-
ления синфазного сигнала. Если отношение с/ш на входе усилителя обо-
значить
как Твх,
то на выходе это соотношение будет определяться:
Y
BbIX
= Ч'вхК^с, (9.33)
где
Косс
=
К
пс
/К
пс
с
— коэффициент ослабления синфазного сигнала,
К
пс
—
коэффициент передачи полезного сигнала, К
псс
—коэффициент передачи
синфазного сигнала помехи.
В общем случае как полезный сигнал, так
и
сигнал помехи можно счи-
тать случайными функциями времени, свойства которых задаются веро-
ятностными характеристиками. Часто бывают известны две из них: ин-
тенсивность сигнала (задаваемая либо среднеквадратичным значением,
либо среднеквадратичной погрешностью) и граничная частота спектра
сигнала'сорр, определяемая полосой частот, в которой сосредоточена боль-
шая часть мощности сигнала
На рис. 9.52 приведен пример спектрального состава полезного S
0
(co)
и шумового S„(co) сигналов е граничными частотами спектра co
rpc
и С0гр
>п
соответственно.
Если на выходе устройства, несущего полезный сигнал и сигнал по-
мехи, поставить фильтр нижних частот с частотной характеристикой
277
