Поляков А.А., Кольцов В.М. Расчет статически неопределимых систем методом сил

Подождите немного. Документ загружается.

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 21 из 58

3.4. Записываем канонические уравнения метода сил:

11 1 12 2 13 3 1

21 1 22 2 23 3 2

31 1 32 2 33 3 1

XXX

δ+δ +δ+∆=

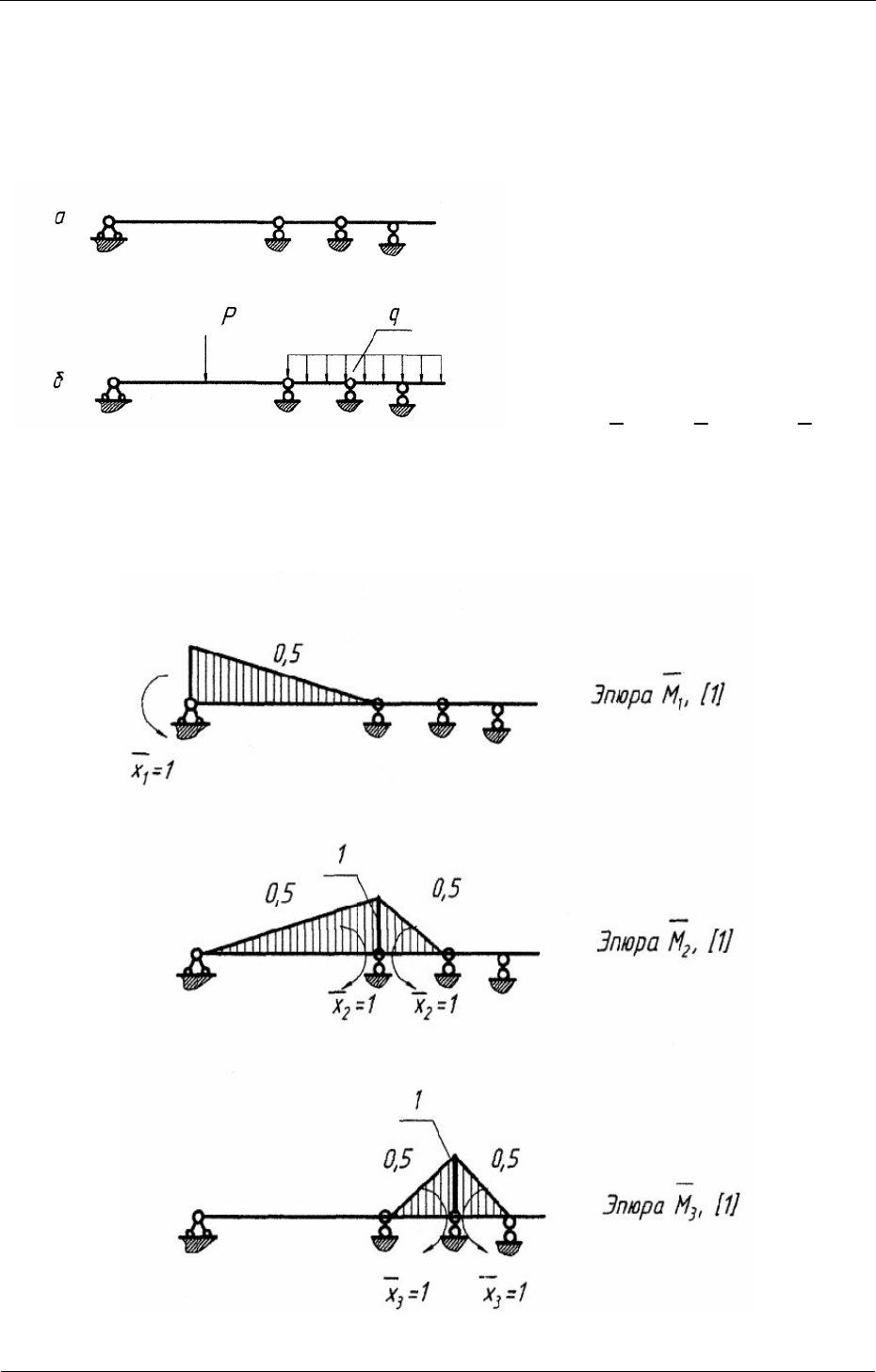
3.5. Строим эпюры изги-

бающих моментов для основ-

ной системы метода сил. Для

этого загружаем принятую

основную систему единич-

ными безразмерными момен-

тами

1,X

1X =

1,X

направление которых выбира-

ем произвольно. Эпюры изгибающих моментов от этого загружения показаны

на рис. 3.7.

Рис. 3.7

Рис. 3.6

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 22 из 58

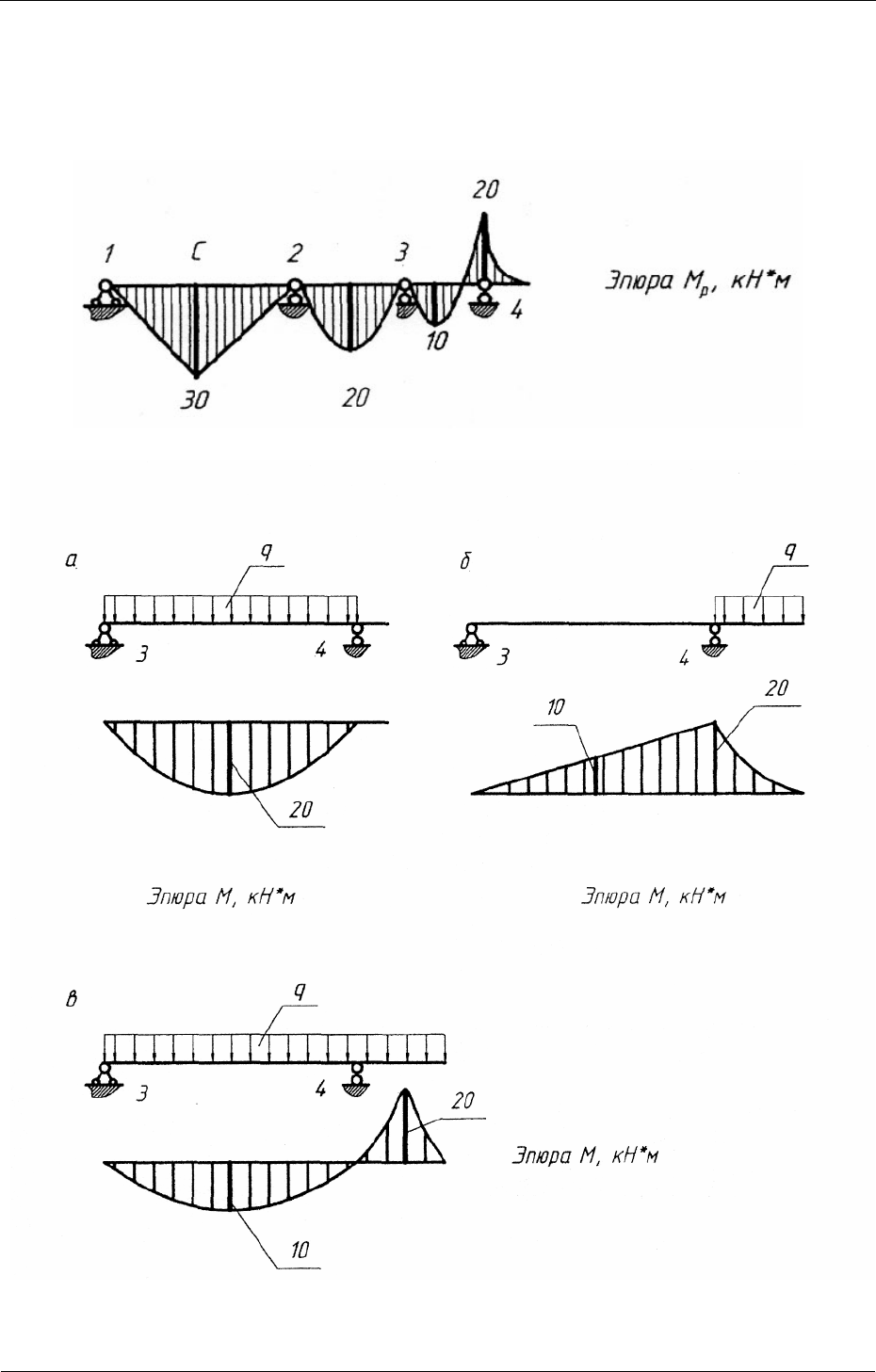
Для построения эпюры изгибающих моментов от внешней нагрузки

(М

) рассматриваем каждый из пролетов как шарнирно опертые балочки, ко-

торые нагружаем внешней нагрузкой Р и q. Строим для них эпюры изги-

бающих моментов и переносим на основную систему (рис. 3.8).

Рис. 3.8

Рис. 3.9

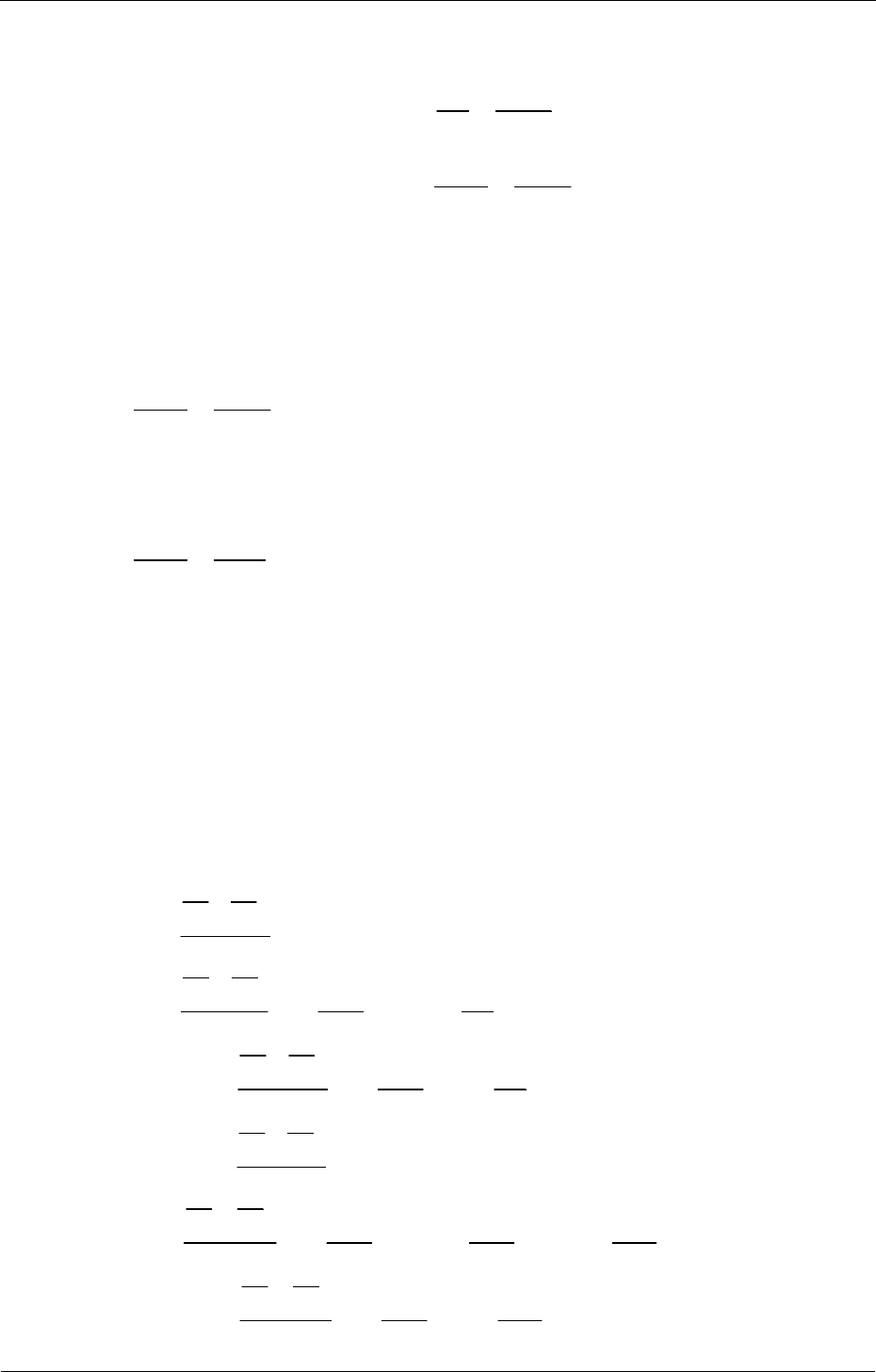
Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 23 из 58

Вычисление значений изгибающих моментов в сечениях каждой из

балочек от внешней нагрузки приведены ниже:

– посередине 1-го пролета

20 6

30 кН м,

⋅

== ⋅

– посередине 2-го пролета

40 4

20 кН м.

⋅⋅

== ⋅

При определении изгибающих моментов в сечениях 3-й балки удобно

использовать принцип независимости действия сил. Так, от распределенной

нагрузки внутри пролета значение изгибающего момента посередине пролета

составляет:

40 4

20 кН м

⋅⋅

=== ⋅

(рис. 3.9, а).

Значение изгибающего момента в сечении балки над правой опорой

от действия консольной нагрузки:

40 1

20 кН м.

⋅⋅

=== ⋅

Посередине третьего пролета значение изгибающего момента от этой

же нагрузки составит:

0,5 20 10 кН мM =−= ⋅ (рис. 3.9, б).

Окончательная эпюра изгибающих моментов для балочки 3-го проле-

та определяется алгебраическим суммированием вышеуказанных эпюр и

представлена на рис. 3.9, в.

3.6. Вычисляем значения коэффициентов канонических уравнений ме-

тода сил по формуле:

⋅

δ=

∑

∫

211 ;

IEI EI

⋅

δ= = ⋅⋅⋅=

∑

∫

12 21

11 ;

IEIEI

⋅

δ=δ= = ⋅⋅=

∑

∫

13 31

⋅

δ=δ= =

∑

∫

628

211 211 ;

663

IEI EI EI

⋅

δ= = ⋅⋅⋅+ ⋅⋅⋅=

∑

∫

23 32

11 ;

IEIEI

⋅

δ=δ= = ⋅⋅=

∑

∫

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 24 из 58

2112 .

IEI EI

⋅

δ= = ⋅⋅⋅⋅=

∑

∫

3.7. Грузовые коэффициенты канонических уравнений метода сил

находим по формуле

⋅

∆=

∑

∫

()

3 3 135

2300,5 130 2300,5 ;

663

IEI EI EI

⋅

∆= =− ⋅⋅ +⋅ − ⋅⋅⋅ =−

∑

∫

()

3 3 2 175

2300,5 2300,5 301 4200,5 ;

66 6 3

IEI EI EI EI

⋅

∆= =− ⋅⋅⋅− ⋅⋅⋅+⋅− ⋅⋅⋅=−

∑

∫

()()

23 60

4 20 0,5 4 10 0,5 20 0 .

66 3

IEI EI EI

⋅

∆= =− ⋅ ⋅ ⋅ + ⋅−⋅ ⋅ + ⋅ =−

∑

∫

3.8. Записываем систему канонических уравнений метода сил:

123

21 135

00;

1 8 1 175

333

1460

00.

333

EI EI EI

XXX

EI EI EI EI

IEIEI

⋅+ ⋅+− =

⋅+ ⋅+ ⋅− =

+⋅+⋅−=

После сокращения канонических уравнений на величину 3

EI получим:

123

6301350;

38 1750;

0 4 60 0.

XXX

++−=

++ −=

3.9. Решаем систему уравнений известными методами и находим не-

известные усилия:

= 15,1 кН м,

= 14,8 кН м,

= 11,3 кН м.

⋅

3.10. Выполняем проверку правильности решения системы уравне-

ний. Для этого подставляем найденные значения Х

в исходные уравнения,

например во второе уравнение, и получаем:

3 15,1 8 14,8 11,3 175 175 175 0.⋅+⋅ + −=−=

Отсюда следует, что решение системы уравнений выполнено верно.

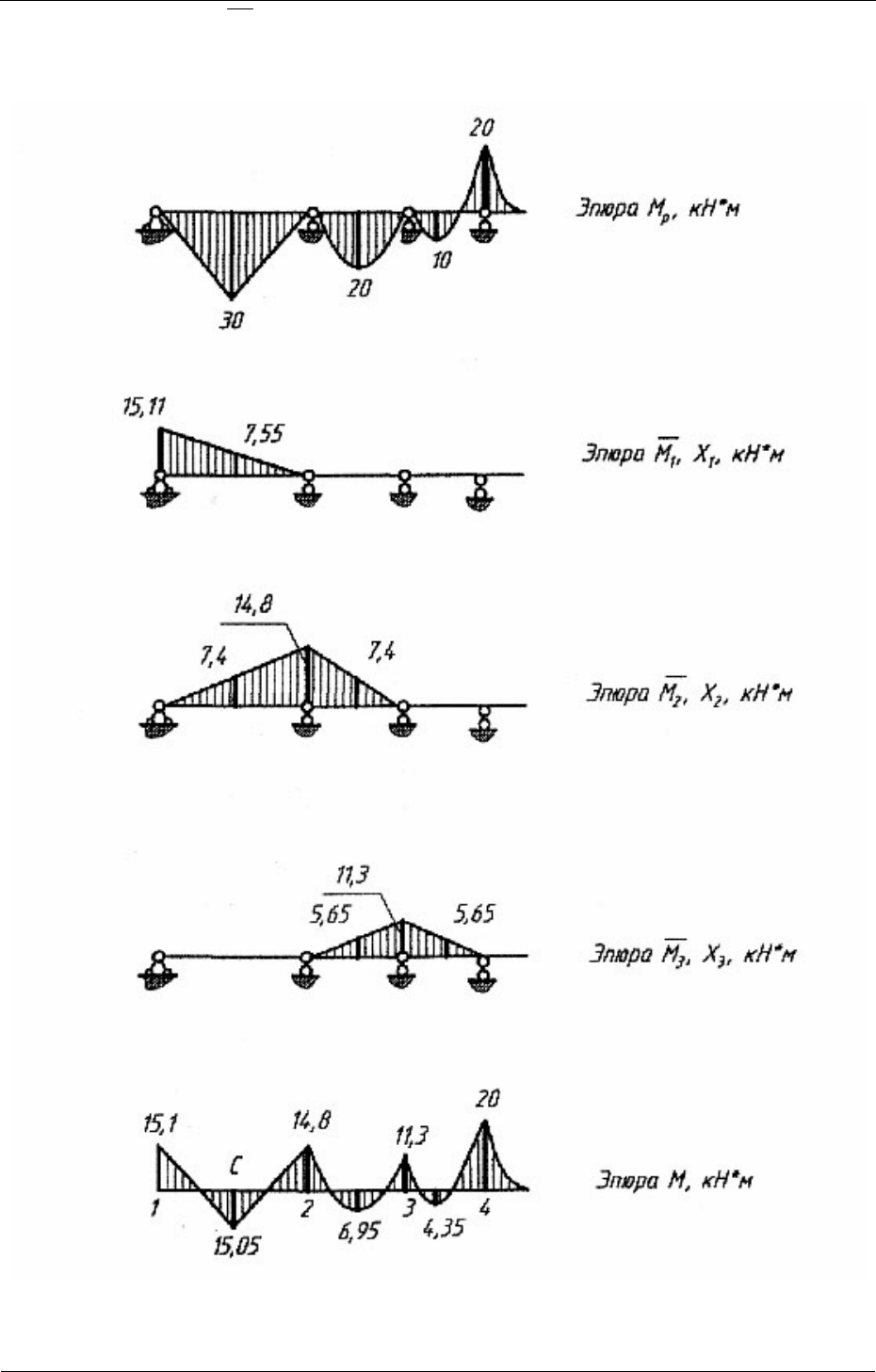
3.11. Строим действительную эпюру изгибающих моментов для задан-

ной системы. Для этого используем принцип независимости действия сил.

Предварительно строим эпюры

⋅

с учетом знаков неизвест-

ных усилий (рис. 3.10, а) и вычисляем действительные значения моментов

в расчетных сечениях, как и ранее, по формуле:

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 25 из 58

MMX=+ ⋅

∑

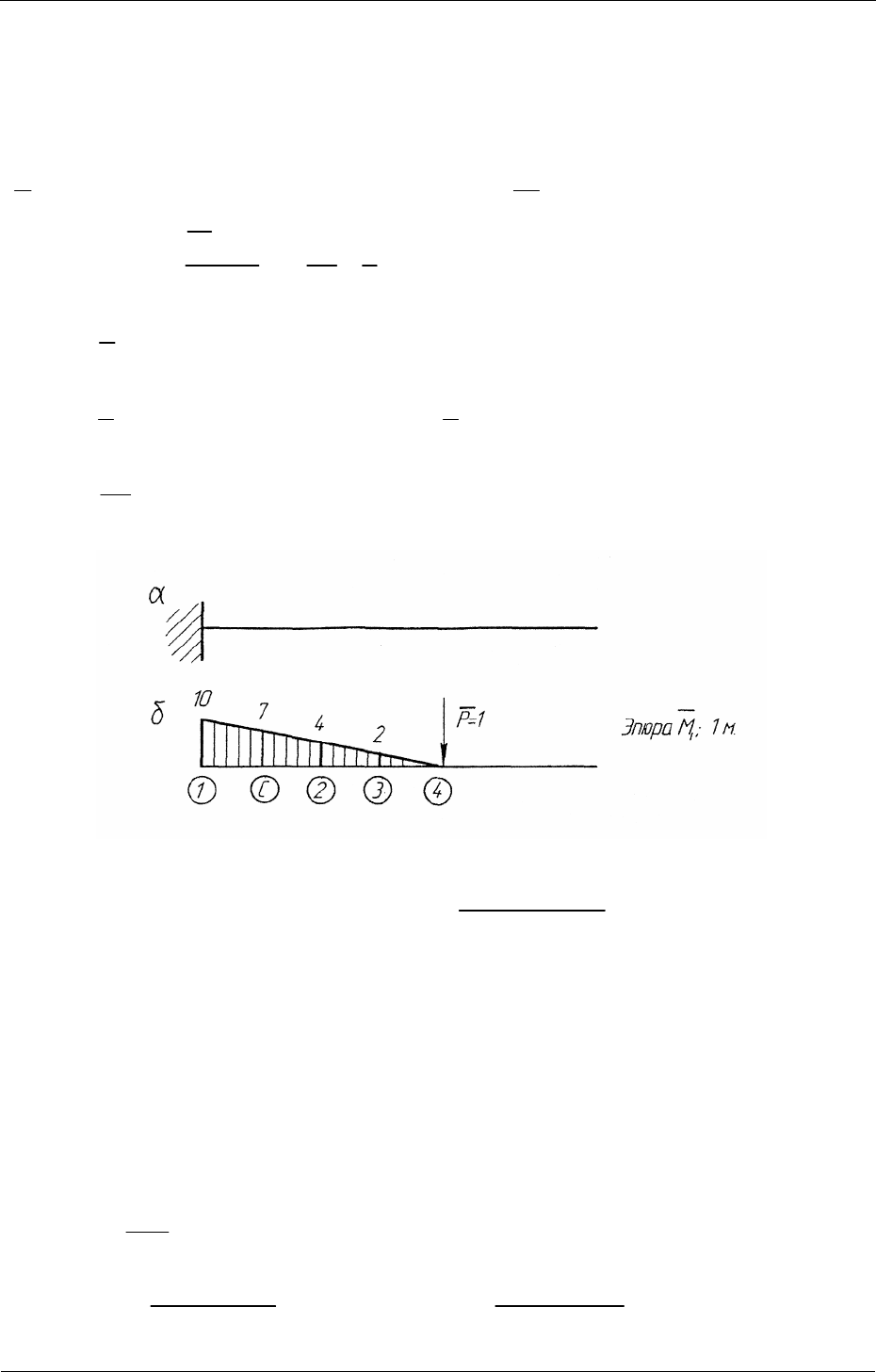
Эпюра действительных изгибающих моментов показана на рис. 3.10.

Рис. 3.10

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 26 из 58

3.12. Выполняем деформационную проверку правильности построе-

ния эпюры изгибающих моментов

М по методу, изложенному в п. 2.8.

Для этого определяем перемещение по направлению отброшенных

(перерезанных) связей. Например, находим перемещение сечения над 4-й

опорой. Основную систему (рис. 3.11, а) нагружаем единичной силой

1P = и строим эпюру единичных моментов

(рис. 3.11, б). Тогда:

()

2 15,1 10 2 15, 05 7 15, 05 10 15,1 7

EI EI

⋅

⎡

∆= = ⋅ ⋅⋅ ⋅−⋅ ⋅− ⋅ + ⋅ +

⎢

⎣

∑

∫

()

2 15,05 7 2 14,8 4 14,8 7 15,05 4

+⋅−⋅ ⋅+⋅ ⋅+ ⋅− ⋅ +

()()

()

14,8 4 4 6,95 3 11,3 2 11,3 2 4,35 1

349,9 345,3 0.

⎤

+⋅ ⋅−⋅ ⋅+ ⋅ + ⋅ ⋅− ⋅ =

⎥

⎦

=⋅ − ≠

Рис. 3.11

Погрешность счета составляет

349,9 345,5

100 1,35%

349,9

−

=⋅=, что впол-

не допустимо.

Примечание. Для определения перемещения по методу Мора можно использо-

вать любую основную систему, в том числе и применяемую в предыдущих расчетах.

3.13. Строим эпюру поперечных сил Q по эпюре изгибающих момен-

тов М путем вырезания стержней по методике, изложенной в п. 2.9.

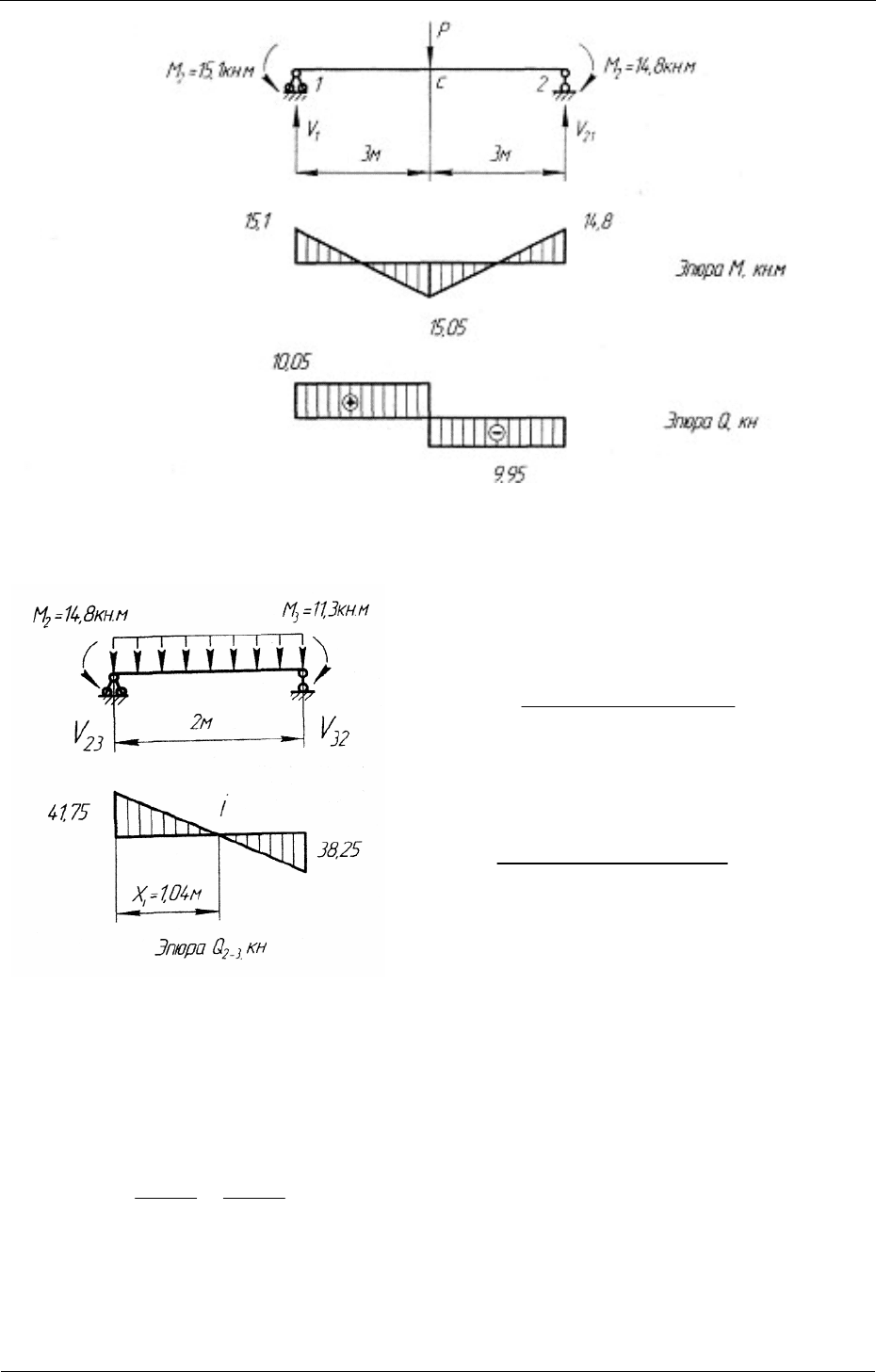
УЧАСТОК 1–С–2 (рис. 3.12). Значение поперечной силы находим по

дифференциальной зависимости:

Qtg

==α

тогда

15,1 15,05 15,05 14,8

10,05 кН;9,95кН.

C С

−−

== = =−

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 27 из 58

Рис. 3.12

Строим эпюру поперечных сил на участке 1–С–2:

0:m

∑

23 23

21 2 0MMq V

−

+⋅⋅− ⋅=

14,8 11,3 40 2 1

41,75 кН

−

+⋅⋅

0:m

∑

23 32

21 2 0MMq V

−

+⋅⋅− ⋅=

14,8 11,3 40 2 1

38,25 кН;

−

−+⋅⋅

23 32

0: 2YVVq

+−⋅=

∑

41,75 38,25 40 2 80 80 0.

+ −⋅=−=

Проверка подтверждает правильность оп-

ределения реакций опор балочки.

Строим эпюру поперечных сил на участке 2–3 (рис. 3.13).

УЧАСТОК 2–3 (рис. 3.13).

Координата сечения где поперечная сила меняет знак:

41,75 41,75

1, 04 м.

===

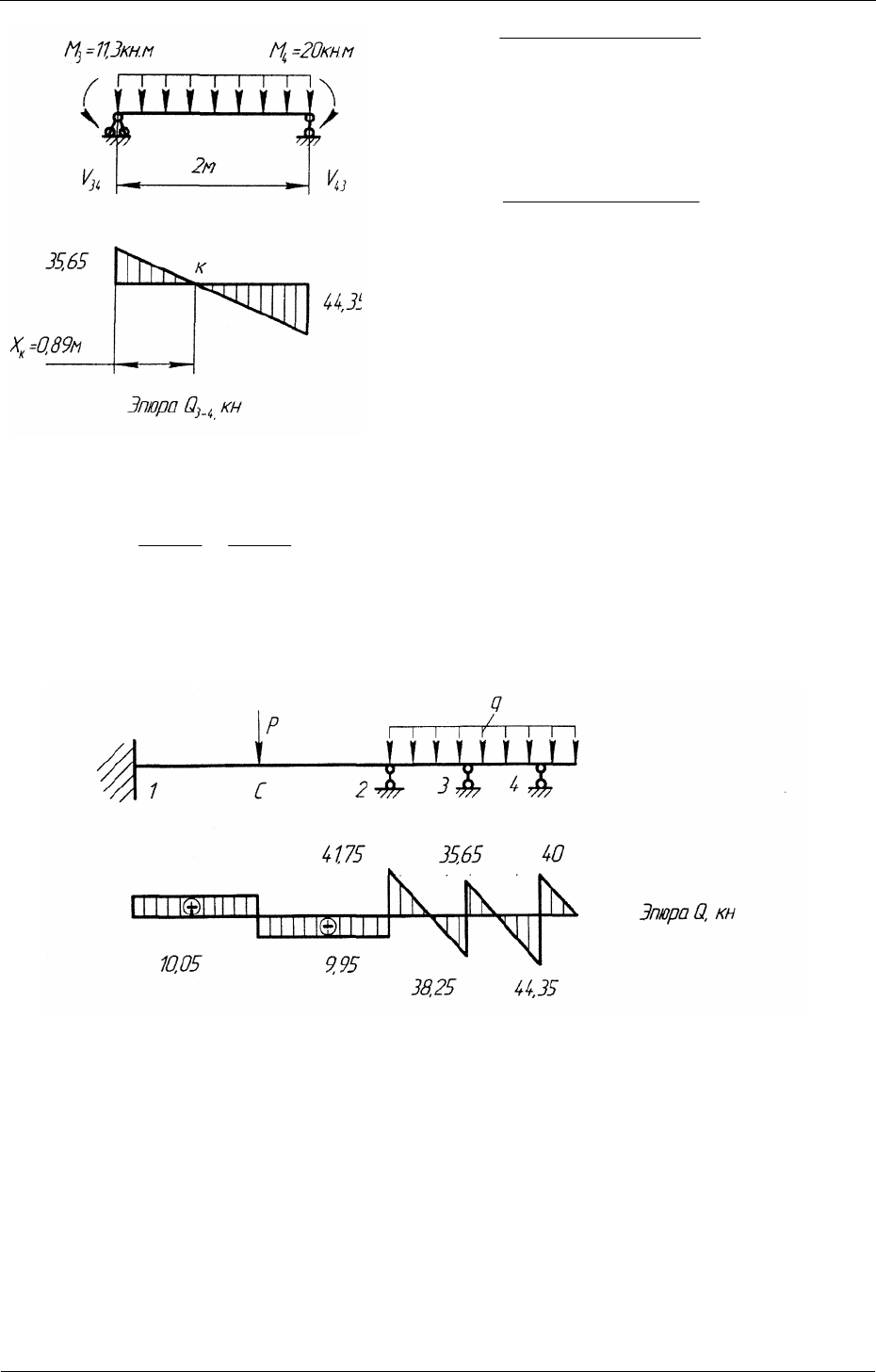
УЧАСТОК 3–4 (рис. 3.14)

0:m =

∑

34 34

21 2 0MMq V−+⋅⋅−⋅=

Рис. 3.13

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 28 из 58

11,3 20 40 2 1

44,35 кН.

−

++⋅⋅

0:m

∑

34 43

21 2 0MMq V

−

+⋅⋅− ⋅=

11,3 20 40 2 1

36,65 кН.

−

+⋅⋅

∑

34 43

35,65 44,35 40 2 0.

VVq

−⋅=

+−⋅=

Реакции опор найдены верно.

Строим эпюру поперечных сил на

участке 3–4.

Координата сечения, где поперечная сила меняет знак:

36,65 35,65

0,89 м.

===

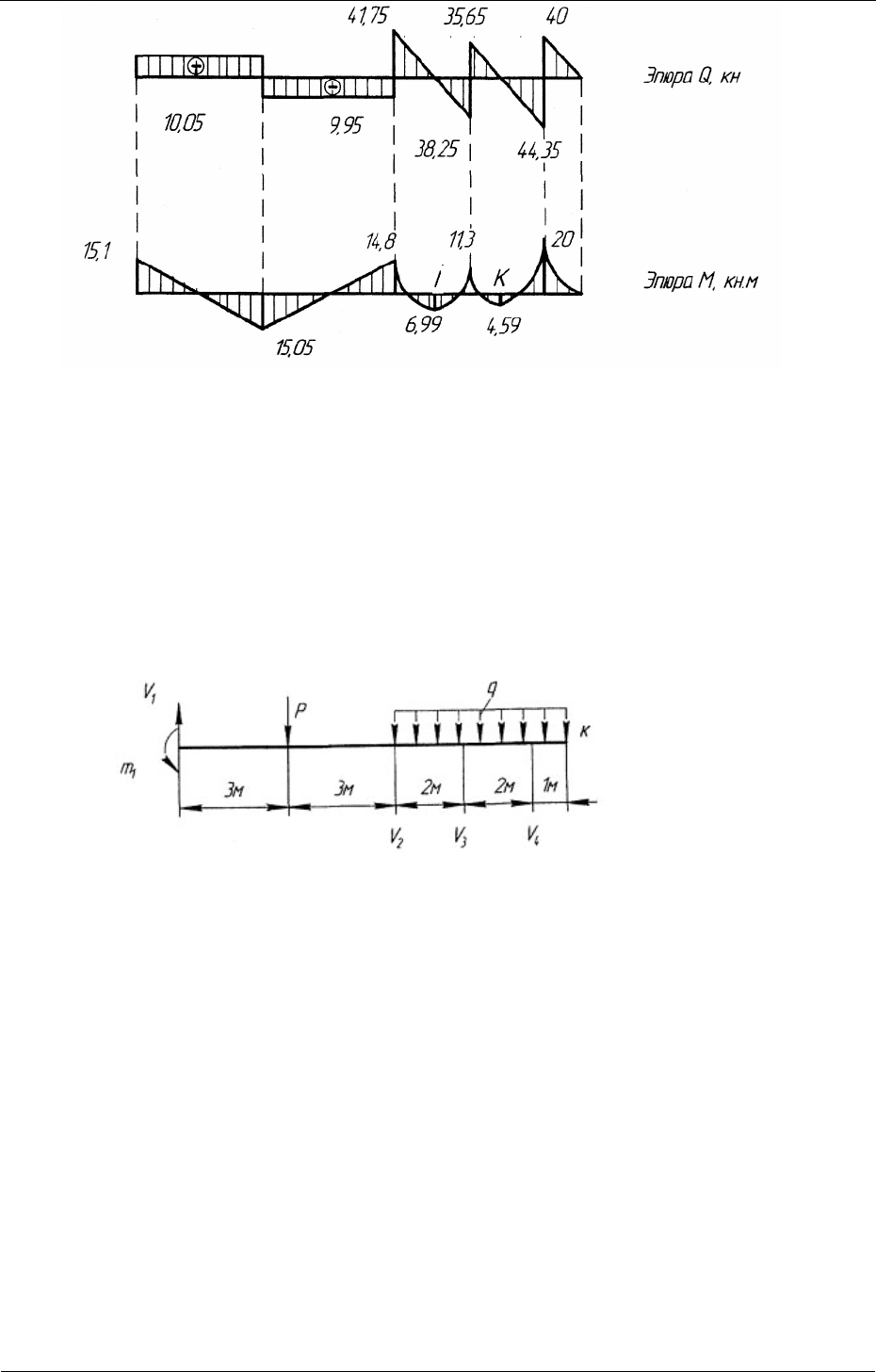
Переносим эпюры поперечных сил, построенные для отдельных проле-

тов, на заданную систему. Эпюра поперечных сил для заданной системы

показана на рис. 3.15.

Рис. 3.15

По эпюре поперечных сил производим уточнение эпюры изгибаю-

щих моментов в сечениях, где

Q = 0. Для этого вычисляем значения изги-

бающих моментов в этих сечениях:

(

)

(

)

40 44,35 2,96 35,65 38,25 0,96 40 3,96 1,98

6,99 кН м;

M =+ ⋅ + + ⋅ −⋅ ⋅ =

=⋅

(

)

40 44,35 1,11 40 2,11 1,055 4,59 кН м

M =+ ⋅−⋅ ⋅ = ⋅

Эпюра действительных изгибающих моментов после уточнения пока-

зана на рис. 3.16.

Рис. 3.14

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 29 из 58

Рис. 3.16

3.14. Определяем реакции опор, для чего используем эпюру изгибаю-

щих моментов и эпюру поперечных сил (рис. 3.16).

10,05 кН;V =

9,95 41,75 51,7 кН;V =+ =

38,25 35,65 73,9 кН;V =+=

44,35 40 84,35 кН;V =+=

15,1 кН м.m =− ⋅

3.15. Выполняем статическую проверку (рис. 3.17):

Рис. 3.17

1234

0: 5

10,0551,773,984,35 52202200.

YVVVVPq

=+++−−⋅=

= + + + −−⋅=−=

∑

11 2 3 4

0: 8 5 3 1 5 2,5 15,1

10,05 11 20 8 51,7 5 73,9 3 84,35 1 40 5 2,5

675,1 675,1 0

mmVPVVVq=−+⋅−⋅−⋅−⋅−⋅⋅=−

−⋅+⋅−⋅−⋅−⋅+⋅⋅=

=−=

∑

Результаты проверки подтверждают правильность решения.

Поляков А.А., Кольцов В.М.

Расчет статически неопределимых

стержневых систем методом сил

ГОУ ВПО УГТУ-УПИ – 2006

стр. 30 из 58

4. Использование свойств симметрии

при раскрытии статической неопределимости стержневых систем

Статически неопределимые стержневые системы называют симмет-

ричными, если они имеют геометрическую ось (плоскость) симметрии, отно-

сительно которой симметрично расположены наложенные на систему связи и

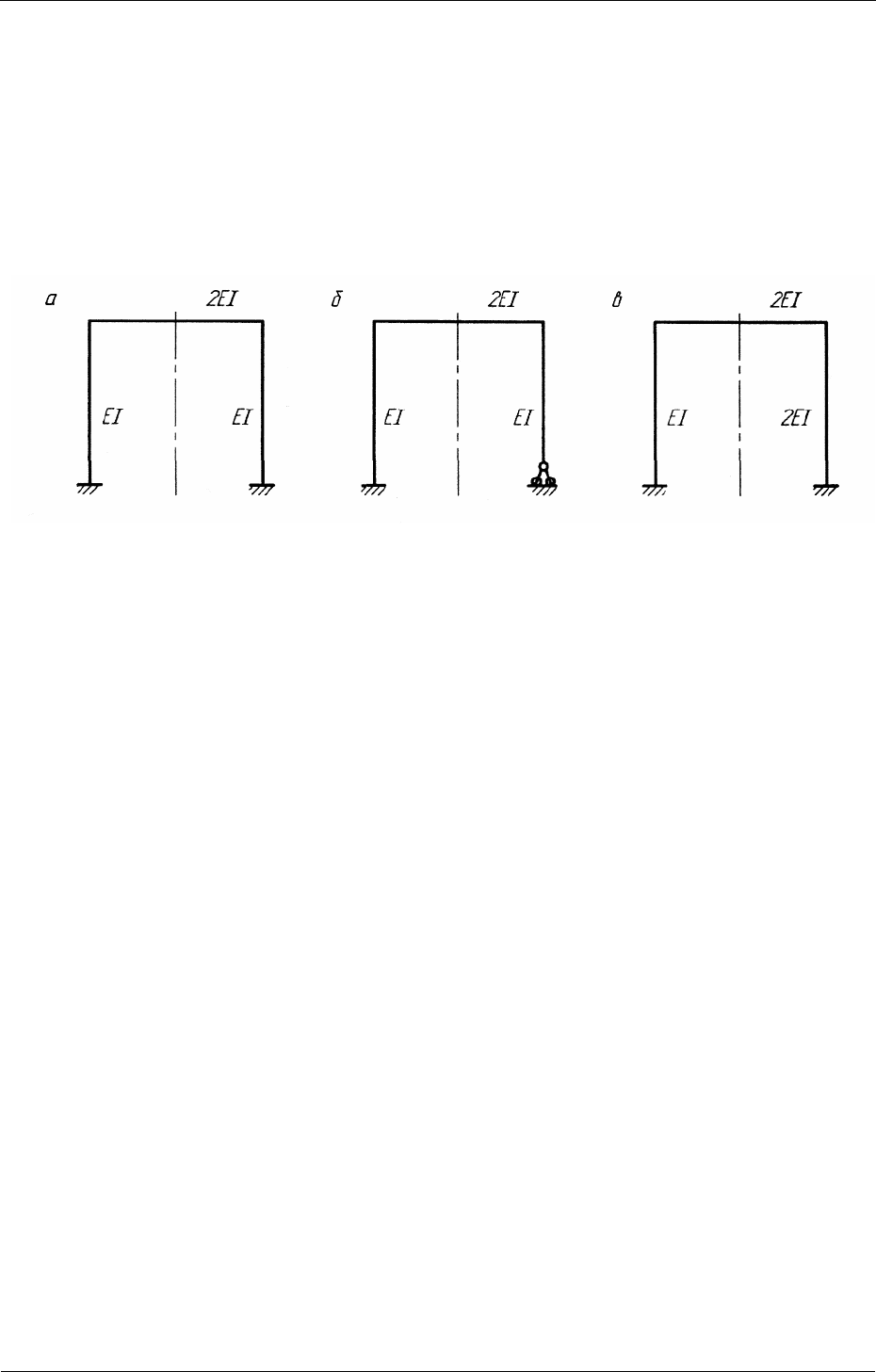
жесткости симметрично расположенных стержней равны (рис. 4.1, а).

Рис. 4.1

В этом случае правая часть системы может рассматриваться как зер-

кальное отображение левой части относительно оси симметрии.

Рамы, представленные на рис. 4.1, б и 4.1, в, не являются симметричны-

ми. В первом случае нарушена симметрия наложенных на раму связей, а во вто-

ром случае различаются жесткости симметрично расположенных стержней.

При расчете симметричных систем

оказывается возможным упростить

решение задачи и снизить число искомых силовых факторов Х

, Х

, ..., Х

Рассмотрим случаи нагружения симметричной трижды статически не-

определимой рамы (рис. 4.1, а) симметричной и кососимметричной нагруз-

ками. Под симметричной нагрузкой будем понимать такую, при которой все

внешние силы, приложенные к правой части рамы, являются зеркальным

отображением сил, приложенных к левой части (рис. 4.2, а). Под кососиммет-

ричной нагрузкой будем понимать такую, при

которой силы, приложенные к

правой половине рамы, также являются зеркальным отображением сил, при-

ложенных к левой половине, но противоположны им по знаку (рис. 4.2, б).

Аналогично классифицируются и внутренние силовые факторы.

Тогда у симметричной рамы в плоскости симметрии при симметрич-

ной внешней нагрузке обращаются в нуль кососимметричные внутренние

силовые факторы, а при

кососимметричной внешней нагрузке - симмет-

ричные силовые факторы.

Так, у рамы (рис. 4.2, а) в плоскости симметрии обращается в нуль

поперечная сила (эпюра моментов симметричная и момент достигает экс-