Плотников В.С. Геодезические приборы

Подождите немного. Документ загружается.

ближенной зависимости

Величина j3, как видно, определяет соответствующую величину базы Ъ

при определенном расстоянии S. Следовательно, предельное расстояние

mdX

определяется полным размером базы (рейки). При коэффициенте

дальномера А' = 100 длина рейки равна 1 м на каждые 100 м измеряемо-

го расстояния.

Постоянный параллактический угол можно получить с помощью сле-

дующих оптических систем:

1) объектив зрительной трубы и сетка нитей в плоскости его изобра-

жения (нитяный дальномер);

2) один оптический клин перед объективом зрительной трубы;

3) два отпических клина перед объективом;

4) децентрированные иолулинзы.

Нитяный дальномер целесообразно рассматривать отдельно (см.

§ 59). Действие оптического клина перед объективом зрительной трубы

описано в § 49 [формула (9.12)].

В случае применения оптического клина для получения постоянного

параллактического угла перед объективом устанавливается ахромати-

ческий клин, перекрывающий часть входного отверстия (использование

принципа двойного изображения). Тогда часть пучка лучей, идущих от

точки М* изображения (рис. 102), проходящая через незакрытую кли-

ном часть объектива, пойдет на выходе параллельно главному лучу, т.е.

по направлению точки М рейки, а вторая часть пучка отклонится клином

на угол /3 и пойдет по направлению PN.

В зрительную трубу будут видны два изображения рейки, смещенные

одно относительно другого на величину / = MN = 5* tg /3. Величина

смещения / отсчитывается по шкале смещенного клином изображения

рейки. По величине / определяют расстояние S от вершины Р дально-

мерного угла до рейки

7ctgj3.

-И/1

Рис. 102. Схема применения одного оптического клина для получения постоянного

параллактического угла

Рис.

103.

Два клина для получения

Рис.

104.

Две полулинзы для получе-

симметричного расположения рейки ния постоянного параллактического

угла

Преломляющий угол клина в рассчитывают по формуле 0 = 0/(я

—

1).

Корректировка заданной величины 0 производится поворотом клина

в его главной плоскости.

При одном клине рейка располагается несимметрично относительно

измеряемой линии. Для обеспечения симметричного расположения рейки

перед объективом помещают два клина, каждый из которых закрывает

половину входного отверстия объектива. Клинья располагаются прелом-

ляющими ребрами в разные стороны, и каждый отклоняет лучи на угол,

равный 0/2 по отношению к оптической оси (рис. 103).

Постоянный параллактический угол можно получить при помощи

двух полулинз (рис. 104). Полулинзы изготавливаются распиливанием

одной линзы по диаметру и устанавливаются перед объективом так,

чтобы линия распиливания располагалась горизонтально. Полулинзы 0\

и О

раздвигаются в противоположные стороны до получения необхо-

димой величины угла 0. Величину смещения d каждой полулинзы рас-

считывают по формуле:

где /'

—

фокусное расстояние линзы.

С учетом того, что коэффициент дальномера К = р/0, получим:

В оптических дальномерах с постоянным углом применяют штриховые

рейки, разделенные через 1-2 см. При наложении двух изображений

рейки штрихи одного изображения попадают между штрихами другого,

и доли деления могут быть оценены на глаз. Если считать, что в лучшем

случае можно оценить десятые доли деления, то при К = 100 ошибка

отсчета составит

10—20

см. Для уменьшения ошибки отсчета исполь-

зуют различные отсчетные приспособления. Простейшим является вернь-

ер,

наносимый на рейке, у которого величина, равная девяти делениям

рейки, делится на 10 частей. Более точный результат дают оптические

микрометры. В качестве такого микрометра может быть применена

0/'

(Ю.5)

2р

Ц>

J Z 1

9 W 11

Рис.105. Дальномерная насадка ДН-04

(разрез):

1 - зажимной винт; 2

—

промежуточ-

ное полукольцо; 3 — котировочный

пинт; 4 — оправа; 5 — пружинное

кольцо; 6 - крышка; 7 - гайка;

8 — колпачок; 9, 10 - оптические

клинья; // - корпус

Ри с. 1 Об. Дал ьно мерная насадка ДН-10

(разрез):

1 — оправа с полулинзами задняя; 2

—

втулка; J — корпус; 4

—

котировоч-

ные винты; 5

—

колпачок; 6

—

оправа

с полулиизами передняя

плоскопараллельная пластинка. Поворотом пластинки совмещаются

штрихи двух изображений смежных делений рейки, и по барабану

микрометра производится отсчет. Микрометр такого типа применен в

дальномсрной насадке ДН-04, в которой в одной половине светового

отверстия расположена ахроматическая пара клиньев, а в другой - плос-

копараллельная пластинка. Конструкция насадки приведена на рис. 105.

В оправе 4 установлены клинья 9 и 10 и пластинка (на рисунке не вид-

на).

Оправа 4 и корпус насадки /У имеют соответственно сферическую

и коническую сопрягаемые поверхности, что позволяет плавно накло-

нять оправу относительно корпуса котировочными винтами 3 для изме-

нения величины параллактического угла (точной установки коэффи-

циента дальномера).

В дальномерах с двумя оптическими клиньями применяется опти-

ческий микрометр с двумя плоскопараллельными пластинками. Плас-

тинки одновременно поворачиваются в противоположные стороны.

В дальномерах с двумя оптическими клиньями оба клина делают

перемещающимися вдоль оптической оси. Как известно (см. § 49),

величина доли деления на рейке может быть отсчитана после совмещения

штрихов по шкале, связанной с перемещающимися клиньями. Общая

длина такой шкалы должна быть равна величине наименьшего деления

на рейке, умноженной на коэффициент дальномера. При величине деле-

ния на рейке 1 см и коэффициенте дальномера, равном 100, шкала

оказалась бы равной 1 м. Ясно, что такая шкала неудобна. Поэтому

оптический микрометр такого типа используется обычно вместе с вернь-

Рис. 107. Оптическая схема компенсатора ДН-10

ером на рейке. Тогда микрометром измеряют лишь величину деления,

меньшую точности верньера (0,1 деления рейки). Для этого точно совме-

щают, пользуясь микрометром, наиболее близкие штрихи на рейке и

верньере и берут отсчет по микрометру. Для этой же цели в некоторых

дальномерах применяют микрометр с плоскопараллельной пластинкой.

Приведем схему и конструкцию дальномерной насадки ДН-10 с посто-

янным параллактическим углом и с использованием принципа двойного

изображения. Главной частью насадки (рис. 106) является оптический

компенсатор, оптическая схема которого приведена на рис. 107.

Компенсатор состоит из пары отрицательных полулинз 2 и 3, изго-

товленных из одной линзы, и пары положительных иолулинз / и 4, ко-

торые также изготовлены из одной линзы для обеспечения равенства

фокусных расстояний полулинз. Параметры полулинз и их расположение

выбираются так, чтобы в целом получилась афокальная оптическая сис-

тема. При этом должно быть:

= d

-S

Если S

> = S

, то d = d

+ 2S

^ или d = /,' (1 - Г

Путем сдвига оптических осей иолулинз с оси насадки на величину А

образуется параллактический угол j3. Контур полулинз оформляется при

их изготовлении с учетом смещегия на величину А:

А =

где /,

линз.

(10.7)

— фокусные расстояния положительной и отрицательной

Афокальная система имеет увеличение в одной половине

V50/89,

в другой

—

V89/90.

Тогда отношение увеличений составит Г

90/89.

Так как компенсатор создает расчетную разность увеличений между

изображениями нониуса и шкалы рейки, нет необходимости во введении

специального микрометра для измерения несовпадения ближайших

штрихов шкалы и нониуса. Роль микрометра выполняет сам компенса-

тор.

Так как оба изображения дал ьно мерной рейки проецируются в плос-

кость сетки трубы под различными увеличениями, при наклоне трубы

эти изображения будут перемещаться не только относительно сетки

нитей, но и относительно друг друга. В ДН-10 разность увеличений 1/90

дает возможность при перемещении нити сетки на всю длину изображе-

ния нониуса (поворотом трубы вокруг ее оси вращения) сместить меж-

ду собой ближайшие изображения шкалы рейки и нониуса на величину

точности нониуса. Отсчет положения горизонтальной нити сетки по шка-

ле нониуса, считая от нулевого штриха, и покажет величину несовпа-

дения.

Длина нониуса /

и увеличение компенсатора Г

связаны соотно-

шением

/„ =

-—(10.8)

где а — длина одного деления шкалы рейки; Ас = 10

—

число делений

нониуса; Г

90/89

—

дополнительное угловое увеличение одного изоб-

ражения относительно второго (увеличение компенсатора).

§ 59. Нитяный дальномер

Нитяный дальномер является простейшим дальномером с постоянным

параллактическим утлом.

Дальномерная сетка состоит обычно из двух или трех нитей. Расстоя-

ние р между нитями сетки определяют по формуле

/об

Р = -^— •

(

где — фокусное расстояние объектива трубы; К — коэффициент

дальномера.

Толщина нитей сетки 5 выбирается с учетом наивыгоднейшей толщи-

ны при рассматривании невооруженным глазом (обычно 5

= 0,08 —

0,1 мм). При фокусном расстоянии окуляра f'

° /' •

(10.10)

250

При появлении зрительных труб с внутренней фокусировкой, которые

в настоящее время применяют во всех геодезических приборах, в свое

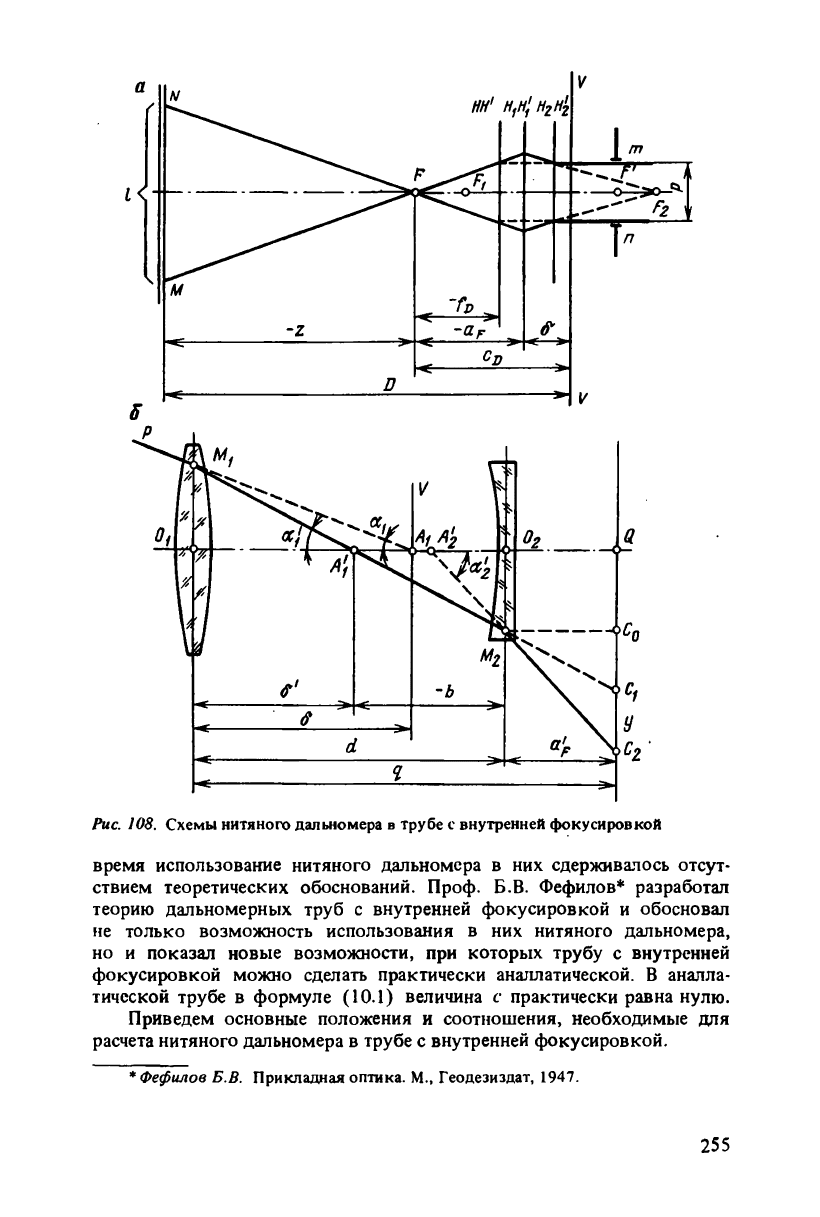
Рис. 108. Схемы нитяного дальномера в трубе с внутренней фокусировкой

время использование нитяного дальномера в них сдерживалось отсут-

ствием теоретических обоснований. Проф. Б.В. Фефилов* разработал

теорию дальномерных труб с внутренней фокусировкой и обосновал

не только возможность использования в них нитяного дальномера,

но и показал новые возможности, при которых трубу с внутренней

фокусировкой можно сделать практически аналлатической. В аналла-

тичсской трубе в формуле

(10.1)

величина с практически равна нулю.

Приведем основные положения и соотношения, необходимые для

расчета нитяного дальномера в трубе с внутренней фокусировкой.

* Фефилов Б.В. Прикладная оптика. М., Геодезиздат, 1947.

Расчет трубы с внутренней фокусировкой приведен в § 34. Здесь

уместно отметить лишь относящееся к нитяному дальномеру. На

рис.

108, а представлена оптическая схема трубы с внутренней фокуси-

ровкой с нитяным дальномером.

Телеобъектив трубы состоит из двух компонентов: собственно объ-

ектива И\И[ и отрицательной фокусирующей линзы

Линия

—

вертикальная ось вращения прибора; NM - рейка; тп - плоскость

сетки нитей, сопряженная с плоскостью рейки, точки М и N рейки

изображаются соответственно точками т и п. Расстояние D от рейки

до оси вращения прибора VV будет равно:

= -z - a

+5.

Из подобия треугольников NMF и ABF, в которых NM

—

отрезок

рейки, соответствующий расстоянию между нитями на сетке пт =

АВ = р, следует

'о

где f'

- фокусное расстояние телеобъектива (эквивалентноефокусное

расстояние системы объектив

—

фокусирующая линза), когда система

отфокусирована на рейку MN. Подставляя значение z в формулу

для Д получим:

D = -J- I + (5 - J

). (10.11)

Формула

(10.11)

является общей для определения расстояния D для

любой конструкции дальномерной трубы.

В этой формуле по аналогии с предыдущим f'p/p = K

- коэффи-

циенту дальномера, а 5 — йр = C

— второе постоянное дальномера,

или аддитивный член.

Если расстояние между компонентами оптической системы при фо-

кусировании на разные дистанции не изменяется, то не изменяются и

величина эквивалентного фокусного расстояния, и координаты ар. Но

сама идея трубы с внутренней фокусировкой предполагает изменение

расстояния d между компонентами перемещением фокусирующей

линзы при фокусировке, поэтому изменяются эквивалентное фокус-

ное расстояние и координата ар, а следовательно, являются перемен-

ными величинами коэффициент дальномера K

и аддитивный член C

Обозначим величину эквивалентного фокусного расстояния системы

телеобъектива при фокусировке на бесконечность через /'. Тогда =

/' + При этом формула

(10.11)

примет вид

— l+( /+5-Дг.).

(10.12)

Р Р

В формуле

(10.12)

отношение jf'/р = K

- коэффициент дальномера,

остающийся постоянным для всех фокусировок, а величина в скобках,

содержащая переменные величины и являющаяся по сути аддитивным

членом, - переменная. Обозначив второй член формулы

(10.12)

через

, получим:

= / +СА.

(10.13)

В трубе с внутренней фокусировкой аддитивный член Ср не может быть

равен нулю. Однако даже при малых расстояниях D его величина может

принимать пренебрегаемо малые значения по сравнению с D.

Найдем наивыгоднейшее положение фокусирующей линзы, вблизи

которого ее перемещения при фокусировке вызовут лишь минимальные

изменения аддитивного члена C'

. Схема расположения компонентов

представлена на рис. 108, 6~.

Отметим, что направление луча РМ \, направленного в аналлатиче-

скую точку Л\, положение самой аналлатической точки А

, величина

угла c*i, положение изображения А

точки А

через объектив О

и ве-

личина угла а[ не зависят от перемещения фокусирующей линзы 0

В то же время луч

меняет свое положение при перефокусировке,

вследствие чего изменяются положение точки А

и величина угла а

Отметим также, что расстояние A[Q - -b + а'р* при перефокусировке

остается постоянным.

Продолжим луч Л/,Д/

до пересечения с сеткой нитей в точке С

Замечаем, что отрезок QC

при перефокусировке остается неизменным,

а отрезок С\С

изменяет свою величину, так как меняет положение

точка С

. Из треугольников М

и М

имеем:

tg а'

= a'

tg а

;

=М

iga\ =

ap>xga\.

Тогда

- С

С\ = a'

(tga'

tga',).

Из треугольников

А[0

А'

получим:

= А\()

tga,' = А\0

tga

откуда

А\0

tga

—г—

tgal.

Принимая во внимание, что точки А[ (Л

) и А

являются сопряженны-

ми относительно фокусирующей линзы, по формуле отрезков получим:

л\О

Гг

А\О

+]i

17 B.C.

Плотников

Тогда, подставляя значение

предыдущую формулу, напишем:

Aio

+ f

;

ji-b

tgo

= Т, tga, = — tga,.

Далее находим:

C,C

= -a'

. -^-tgo,'. (10.14)

Определим условия,

при

которых значение

—

будет экстремаль-

ным

и,

следовательно, изменение этого значения

при

фокусировании

—

минимальным.

Для

этого продифференцируем выражение

(10.14):

dy = {a'pidb

+bdaj?t).

Так

как

—b+a'pt

const,

то

дифференциал этого выражения равен

нулю,

т.е.

-db +

= 0.

Отсюда

db =

da'pt,

поэтому

dy = —{b + ap,)db.

Исследуем функцию

на

максимум

минимум.

Так как /

' -

величина

отрицательная,

а tg a, —

величина положительная,

то ; > О.

Исследуем абсолютные значения

b и а'р*.

Если абсолютное значение

\b\

> \а'

»|, то — < 0 (так как b < 0, а а!, t > 0).

Если

по

абсолют-

ной величине

\b\ < \а

|, то > 0.

Следовательно, имеет место

минимум функции.

Приравнивая первую производную

—-

нулю, получим:

dy tga|

—

= —р— ib

a'p.) = 0. (10.15)

a'i

Так

как

величина

;—

конечна, уравнение

(10.15)

может быть удов-

летворено

при

условии

Ь + а'р

= 0,

откуда

-aj.,.

(10.16)

Из равенства

(10.16)

можно сделать важный вывод: изменение величи-

ны

у, г

значит,

величины

дальномера будет минимальным, если

будут равны абсолютные величины расстояний

* от

фокусирующей

линзы

до

сетки нитей

и Ъ от

фокусирующей линзы

до

изображения

Л[

через объектив точки

A i

(проекция вертикальной

оси

вращения прибо-

ра

на

оптическую

ось

трубы).

Точки

А\ и А[

являются сопряженными относительно объектива,

поэтому:

где

5 и 5 '

—

расстояния указанных точек

до

объектива.

Из

рис. 108,6

также имеем:

= 5' - d,

где

— расстояние между объективом

фокусирующей линзой. Под-

ставляя значение

5' в

выражение

для 6,

получим:

5+/,'

Имея

виду известные

оптике формулы, можно написать:

5 +/,

где

—

фокусное расстояние эквивалентной системы (телеобъектива).

Учитывая,

что q - d =

а'р

»,

последнюю формулу можно представить

в виде:

+ q-2d = 0.

Таким образом,

при

расчете нитяного дальномера

трубе

внутрен-

ней фокусировкой

при

условии

ее

практической аналлатичности

при за-

данных

/', q, 5

величины

/,', /

' и d

можно найти

при

совместном

решении уравнений: