Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Thermodynamics of Continuous Media 63

2.2. Fluid statics

2.2.1. General equations of fluid statics

2.2.1.1. Stresses in a fluid at rest

We designate as a fluid any body which is in either a liquid or a gaseous state. In

contrast to solids, fluids do not have any intrinsic shape. They adapt to the shape of

the container in which they are found. On the microscopic scale, there is no longer a

crystalline structure, and the molecules, ions, etc., interact by means of

intermolecular forces and collisions. On the macroscopic scale, fluids generally have

isotropic properties; the forces in a fluid at rest are thus represented at each point by

a spherical stress tensor

which depends on a scalar quantity p, designating

pressure. The force

exerted on an elementary surface ds by the material situated

on the same side as the positive normal is (Figure 2.6a):

dsnpfddspndsnpdf

ijiji

  

2.2.1.2.

Conditions for the existence of equilibrium in a fluid

A fluid in equilibrium is only subjected to pressure forces and to external forces

of mass density

. By considering the net force balance on a domain D, we obtain:

0. 

³³

6 D

dvgdsnp

[2.17]

-p.n ds

(a) (b)

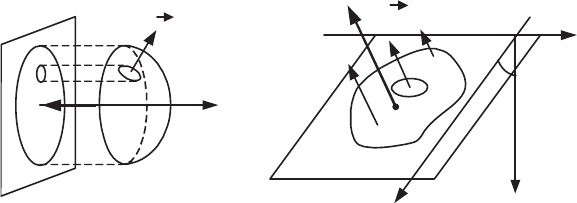
Figure 2.6. (a) Pressure force on a surface; (b) Laplace’s law

Using the identity

³³

6 D

dvfgraddsnf ..

, we obtain:





[2.18]

64 Fundamentals of Fluid Mechanics and Transport Phenomena

Equation [2.18] can only be solved if the vector

U

can be derived from a

potential, in other words if the following condition is satisfied:



0  ggradgrotgrot

GGG

UUU

We can see that for a fluid of constant density,

an equilibrium situation can only

exist if the force field

Ugradg 

derives from a potential

Supposing that

the force field g

can be derived from a potential U

(

Ugradg 

)

the preceding condition can be written:

 Ugradgrad

This leads to the fact that surfaces of

U

=const. and U=const.

are identical.

Equation [2.18] then becomes:

0  Ugradpgrad

[2.19]

This also leads to the identity of isobaric and equipotential surfaces that are

identical. If the fluid is

divariant

, with an equation of state in the form



Tpp ,

the said surfaces are also

isothermal

For example, in the case of gravitational forces, equilibrium is only possible if

the horizontal surfaces are isothermal. If this condition is not satisfied,

natural

convection

will occur.

The resultant pressure force on the exterior of the closed surface

can be

immediately deduced from relation [2.17]:

³³

 

6 D

dvgdsnp

This force is the opposite of the sum of the forces exerted by the force field

on the fluid contained in

Let us now consider the case of gravity. As with equation [2.17], the balance

moment of forces on domain

D –

where

is the center of gravity of this domain

filled with the fluid – can be written:

Thermodynamics of Continuous Media 65

3 3 3

³³³

6 DD

dvMgdvgMdsnpM

which is zero from the definition of the center of gravity.

So, the collection of the pressure forces is equivalent to a single force, equal to

the weight of fluid displaced and applied at the center of gravity

3

of the domain

supposed to be filled with the fluid. The point

is called the

center of buoyancy

This result constitutes

Archimedes’ theorem

Now, considering a vertical cylinder with identical horizontal bases, we see that

the difference in pressure forces between the lower and the upper bases is equal to

the weight of fluid contained in the cylinder

2.2.1.3

. Solution to the general hydrostatic equation

If the preceding conditions are satisfied, the pressure satisfies equation [2.19].

The conditions for the existence of the solution (stratification of the space into

identical surfaces

=const,

=const, etc.) for a fluid whose equation of

state is



Tpp ,

leads, under equilibrium conditions, to the relation



between

and

. We often say that such a fluid is

barotropic

(which is not strictly

true, as this is not a property of the fluid, but of the configuration studied).

We can thus define the function

ph )(

such that:

pgrad

hgrad

If the specific fluid entropy is constant over the entire domain studied, it is said

to be homoentropic, and the function

is therefore the specific fluid enthalpy.

General equation [2.19] can be written as:



 Uhgrad

and its solution is:

const  Uh

. The pressure

can thus be obtained by inverting

the function

h(p).

In the case of gravity, the function

is equal to

, where

designates an

increasing vertical coordinate.

66 Fundamentals of Fluid Mechanics and Transport Phenomena

2.2.1.4.

Equilibrium of an incompressible fluid

2.2.1.4.1. Hydrostatic equations

Such a fluid is generally either a liquid or a gaseous domain of limited vertical

extent, such that its density can be considered constant. We thus consider density to

be independent of pressure, which may eventually be a function of the coordinate

If the fluid is considered to be of uniform density

, we have:

const (U gz for gravity potential)

pUp



So, it is this quantity



(in the case of gravity

gzp



) and not the

pressure alone which is constant in a motionless fluid. Hence,

variations of this

quantity must be the causes of movement

. For this reason, we will call it “driving

pressure” and we will note it as

gzpp

g 0



in the case of gravity.

In fact, for such an incompressible homogenous fluid, we will find (see Chapter

4) that, under certain conditions, movement is associated with variations of this

driving pressure alone, without explicit intervention from pressure.

EXERCISES –

1) Equilibrium of a homogenous liquid in a rotating reference frame of axis O

Give the expression for pressure as a function of the coordinates

and

. Show

that in a reference frame which rotates with angular velocity

about the vertical

axis O

, the isobar surfaces are paraboloids of revolution about the axis O

(Answer:

22 2

const

)

p(xy)gz

UZ U

2) Equilibrium of a homogenous liquid in a reference frame which is undergoing

a constant horizontal acceleration

J

. Derive an expression for pressure as a function

of the abscissa

parallel to the acceleration and the altitude

. Show that in this

reference frame isobar surfaces are inclined planes.

(Answer:



const

)

  pgzx

2.2.1.4.2. Conditions at fluid-fluid interfaces

Continuity of the pressure between two immiscible fluids is only guaranteed if

the interfacial surface is a plane. If this is not the case, the interface behaves in many

respects like a membrane; its constant surface tension is characterized by the set of

the two fluids, if they are pure, and generally decreases with temperature. The

pressure discontinuity

pp 

across the interface is given by Laplace’s law:

Thermodynamics of Continuous Media 67

 

and

are the radii of curvature of two interfacial surface sections by

perpendicular planes which contain the normal to this interface at the considered

point of this one. The pressure

is greater on the concave side of the surface

(Figure 2.6b).

On the other hand, the contact angle between an interface and wall is a physical

characteristic between these three domains [BEN 06]. A liquid wetting the wall

perfectly is joining tangentially to another liquid (water on a clean wall made of

glass, for instance). Surface active substances generally ensure a perfect wetting of

the surface, but they modify the value of the surface tension.

2.2.1.5

. Equilibrium of the atmosphere

By limiting ourselves to the troposphere (lower limit of the stratosphere), the

atmosphere can be considered to comprise a homogenous mixture of nitrogen and

oxygen, and it is characterized by a rapidly decaying temperature with increasing

altitude. It is not in thermodynamic equilibrium, because as oxygen is more dense

than nitrogen, it should be more concentrated in the lower layers. In fact, the

atmosphere is constantly undergoing movements whose characteristic time is small

compared with the time required for the temperature to become uniform. The

atmosphere is in fact

perfectly mixed

: in the movement of large air masses, the

atmosphere undergoes rapid compression and rarefaction, which occur

isentropically, and so during their movement air masses do not have the time to

exchange heat by thermal conduction. This mixing leads to an atmosphere at

constant entropy. Experiments confirm that the Earth’s atmosphere is in a state

which is very nearly homoentropic. This condition defines the standard atmosphere,

whose differences from reality, in the order of a few percent, are due to

meteorological phenomena.

EXERCISES

–

Calculate the pressure

as a function of the altitude

1) in an isothermal atmosphere of temperature

: (





exp

zzg

);

2) in a homoentropic atmosphere, where the temperature at the ground is equal to

68 Fundamentals of Fluid Mechanics and Transport Phenomena

2.2.1.6.

Stability of equilibrium solutions in stratified fluids

A stratified fluid with horizontal surfaces of constant density is in an

equilibrium situation in the gravitational field. The stability of this fluid can be

tested in an elementary way by displacing a fluid particle and observing whether

or not it undergoes a restoring force. Let us first of all consider an

incompressible

fluid whose density, which depends only on temperature,

increases with increasing altitude. A fluid particle which is displaced in the

upward direction finds itself in a region of heavier fluid; it thus undergoes a

greater thrust, and its movement upward is amplified.

The same reasoning applied to a

compressible

fluid (the atmosphere for

example) leads to the following situation: as the displacement occurs

isentropically, it is the specific entropy of the particle which must be compared

with that of the local environment into which the fluid particle is moved. If the

local entropy of ambient fluid falls as the fluid particle rises, the temperature of

the particle is greater than that of this ambient fluid: the Archimedes force thus

increases and the fluid particle comes up.

In conclusion, we have

equilibrium stability of a fluid if its temperature (or

its entropy) increases with increasing altitude

. In the opposite case, the fluid

system is unstable.

2.2.2. Pressure forces on solid boundaries

2.2.2.1.

Constant pressure

A constant pressure situation occurs in numerous applications: pipe-systems

and compressed-air reservoirs, water-distribution networks, etc., where the

effects of an external force field is often negligible as a result of the high

pressure levels which occur within the system.

Consider a surface

(Figure 2.7a) with normal

on which uniform pressure

is exerted, the pressure force on this surface

is:



dsnpF

Letting

ds'

be the projection of the elementary surface

on the plane

perpendicular to the direction Ox, the component

on the axis

can be obtained

from:

'.'..

SppdsdsnxpF

  

³³

Thermodynamics of Continuous Media 69

The

component of the uniform pressure force in the direction Ox is equal to the

pressure force on the surface S', which is a projection of S on the plane

perpendicular to Ox

3

T

(a) (b)

S’ S

ds'

Figure 2.7.

Pressure forces: (a) arbitrary surface with constant pressure;

(b) forces due to a liquid on a plane surface

In practice, this surface is an element of a pipe, a reservoir, etc. Let us take the

example of a cylindrical pipe with radius

. The stress

on the wall, due to the

overpressure

in the pipe, must balance the pressure forces on a half-cylinder. It is

thus equal to

'pR

per unit length:

the stress on the wall increases with the radius R.

For a tube of radius 1 cm transporting compressed air pressurized to 100

atmospheres, this is equal to 10

N/meter.

Pipeline and reservoir dimensions (

diameters

) ought to be as small as possible, in

order to avoid technical difficulties related to the wall resistances.

2.2.2.2.

Hydrostatics

The equilibrium of a homogenous liquid (often water) in a gravitational field is

of considerable practical importance, particularly in cases such as water reservoir

walls, sluice gates and boat hulls.

The

pressure forces on a plane surface

, one side of which is covered by a liquid,

are parallel to the wall normal: they are thus equivalent to a single vector applied at

a given point on the wall, the

center of pressure 3

. Consider a plane surface

identified by the coordinates

Oxy

in its plane (Figure 2.7b). Suppose that the free

surface of the water is at

z = 0

. The hydrostatic pressure is equal to

'p =

U

g z

Denoting the center of inertia of the surface

, the

thrust

(the resultant

pressure force) is equal to:

SpSgzSygydsggzdsP

GGG

³³

UTUTUU

.coscos

70 Fundamentals of Fluid Mechanics and Transport Phenomena

The

thrust P

is equal to the

product of the pressure at the center of inertia G of

the homogenous surface and its surface S.

The center of pressure, which can be

easily calculated by taking the moment of the pressure forces with respect to

, is

beneath the inertia centers.

The forces exerted by water on the walls of large reservoirs and dams are often

considerable; the construction of dams thus involves massive elevations of earth

whose weight blocks the mass of water (weight dams), or large concrete

constructions which resist by returning the thrust on the rocky walls (mountain arch

dams).

The reader can easily verify that the

horizontal component

(along

) of the

hydrostatic pressure force on a curved surface is equal to the hydrostatic pressure

force on the surface

, which is the projection of

on a plane perpendicular to

Ox.

This result clearly makes no sense for a vertical component.

EXERCISES

–

1) Calculate the coordinates of the pressure center

on the surface

of Figure

2.7b. (Answer:

SIyy

GGy



giving the inertia moment of

the surface taking with respect to a straight line parallel to

and passing through

2) Calculate the load-force generated on a vertical rectangular wall, 4 m in width

and containing a mass of water 3 m in height. Determine the position of the center of

pressure. (Answer: 18.0 ×10

newtons, 1 m above the bottom.)

3) Answer the same questions for a dam in the form of a 50 m high equilateral

triangle.

2.2.2.3.

Floaters

A floater is a body placed on the surface of a liquid, and whose weight is less

than that of an equivalent volume of the same liquid. In this kind of situation there is

always an equilibrium position, such that the force exerted by the fluid on the body

balances its weight. However, the stability of this position is not guaranteed. We will

not study hull-stability problems ([BAR 01]) which requires geometrical knowledge

related to surface curvature and normal fields ([KRE 91]).

We will only discuss a simple example in order to illustrate the origin of such

problems. Consider a homogenous, elliptical cylinder whose density is half that of

water, such that at equilibrium, the center of the ellipse is always in the plane free

surface of the water. While in equilibrium, the upward thrust which the cylinder

experiences,

, applied at the center of buoyancy

3

opposes that of its weight,

applied at the center of gravity of the ellipse,

, which lies in a vertical section of

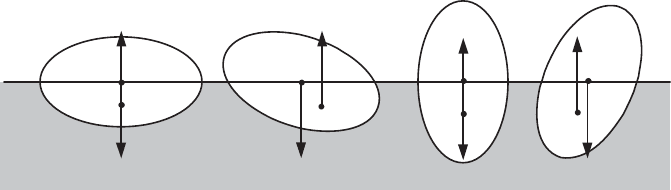
Thermodynamics of Continuous Media 71

the meridian plane of the cylinder. There are two equilibrium positions ((a) and (c)

in Figure 2.8) corresponding to the vertical positions for each axes of the ellipse.

The equilibrium stability is studied in the usual way: a small clockwise rotation of

the cylinder is performed (positions (b) and (d) in Figure 2.8).

GGG

(a)

(b) (d)(c)

Figure 2.8.

Stability study of a floater whose cross-section is elliptic

We assume that the submerged volume (beneath the flotation plane) and the

thrust

remain constant during the displacement; however as the distribution of

the volume submerged has changed, the center of buoyancy

is moved to the

side where the submerged volume has increased (with respect to the vertical

passing through

), thus creating either a restoring moment (situation (b)) or an

amplifying moment (situation (d)), depending on the situation: position (a) is

stable, whereas position (c) is unstable.

In fact for a real hull we must also take account of the way it is loaded, and

possible movements of this load. For the preceding elliptical floater, we see that

we can add a weight to the upper surface of the cylinder: the system will be

stable as long as the restoring moment is less than the moment generated by the

extra weight. On the other hand, a circular cylinder is in a state of neutral

equilibrium if it is not loaded; it obviously becomes unstable if any weight is

added to the upper side. Escorting floating logs during their floatation down

rivers is not a straightforward use of fluid statics!

72 Fundamentals of Fluid Mechanics and Transport Phenomena

2.3. Heat conduction

2.3.1. The heat equation

By inserting expression [2.15] into relation [2.10] we obtain a thermal balance

equation:

VOU



which, if the thermal conductivity of the medium

O

is constant, becomes:



''

with

VOU

In the absence of thermal power sources (

= 0), we obtain the heat equation:

The thermal diffusivity

can be expressed in meter

/second.

2.3.2. Thermal boundary conditions

Here we will deal with the principal problems of heat conduction, which we

will later encounter in a similar form when we deal with viscous fluid

mechanics. Thermal boundary conditions can generally be classed in one of the

following categories:

1) Dirichlet condition: the temperature distribution T(M) is known at all

points on the boundary. This is often the case for recipient walls which contain

an agitated fluid, walls which are in contact with highly conductive solids

(metals, etc.); the corresponding practical problems relate to heating, thermal

insulation, etc.

2) Neumann condition: the heat-flux density on the boundary

)(

known at all points M on the boundary. These conditions are found in the

presence of heat sources resulting from the dissipation of other forms of energy,

such as heating by Joule effect, heat produced by nuclear reactors, radiation

absorption, etc.