Петров Ю.П. Очерки истории теории управления

Подождите немного. Документ загружается.

12.

Исследование регуляторов

систем

управления... 775

обеспечивают в данном случае для спектра (164) не обычный ми-

нимум, совместимый с устойчивостью, а гораздо более глубокий,

абсолютный минимум, то нет ничего удивительного в том, что

подход факультета ПМ-ПУ может обеспечивать гораздо лучшее

гарантированное значение критерия качества (162), чем подход

"#°°теории". Примеры были приведены в

[199],

стр. 41—43

и 88—89. Подход "Я"теории", стремящийся к возможно менее

зависящей от частоты со функции (171) часто оказывается

необоснованным.

Что касается синтеза регуляторов, оптимальных для спектров

(164),

то в работе [199] описывались и рекомендовались два ме-

тода.

Приближенный, когда спектр (164) аппроксимировали обыч-

ной четной рациональной дробью

»+а

2р

+...

ч>

(С0)

, 2с, . 2^2 Г"'

стараясь подобрать коэффициенты а

и Ъ

{

так, чтобы анали-

тическая аппроксимация приближалась к 8-функции (то есть,

была велика при

со

= Р и мала при остальных со).

Метод предельного перехода, использующий то обсто-

ятельство, что 8-функция Дирака является пределом многих

обычных непрерывных функций.

Если, например, нужно найти регулятор, оптимальный для спек-

тра 5ф(со) = 5(со) (соответствующий спектру (164) для Р = 0;

этот спектр имеет постоянная сила (р(г) = 1), то достаточно найти

регулятор, оптимальный для семейства спектров (167), а затем

перейти к пределу при а

—»0.

В каждом отдельном случае метод предельного перехода, разу-

меется, громоздок, но зато он позволяет найти гарантирующие

регуляторы в общем виде, сразу для целых классов объектов

управления. Многочисленные примеры приведены в публикации

[199],

стр. 51—66.

176 §

12.

Исследование регуляторов

и систем управления...

Наиболее интересный пример: оказалось, что самый простой из

всех и издавна применяемый пропорциональный регулятор

и = -кх (173)

является гарантирующим для очень широкого класса объектов

управления: для объектов управления вида (161), у которых

функция (165) достигает минимума при ю=0 и полином

А{0) + кВф) — гурвицев. К этому классу относятся очень мно-

гие объекты управления.

Именно гарантирующим свойством объясняется очень широкое

распространение "древнего" регулятора (173) до самого послед-

него времени, несмотря на многочисленные предложения об ис-

пользовании более сложных регуляторов.

Еще один важный результат, опубликованный в

[199],

стр. 66—

74 — это методика построения гарантированных разделяющих

кривых. Дело в том, что критерий качества (162) — это только

промежуточный критерий, полуфабрикат, используемый лишь

при синтезе оптимального регулятора. Вычислив регулятор, оп-

тимальный для некоторого значения множителя Лагранжа т ,

мы лишь потом переходим к окончательному решению — нахо-

дим,

какую точность управления о

можно обеспечить при за-

данном ресурсе управляющего воздействия о„, или (обратная

задача) — какой ресурс управления о

требуется для обеспече-

ния заданной точности с

Оказалось, что в области гарантирующих управлений решение

этой наиболее важной задачи можно получить сразу и непосред-

ственно. В работе [199] были найдены формулы для значений о

и а

, обеспечиваемых

регулятором,

оптимальным для спектра

(164):

а = К>Й .

(174)

* |ДО-р)|

|ад)|

1*ОР>Г

(175)

" |АОР)|

|ВОР)|

12.

Исследование регуляторов

и систем управления... 177

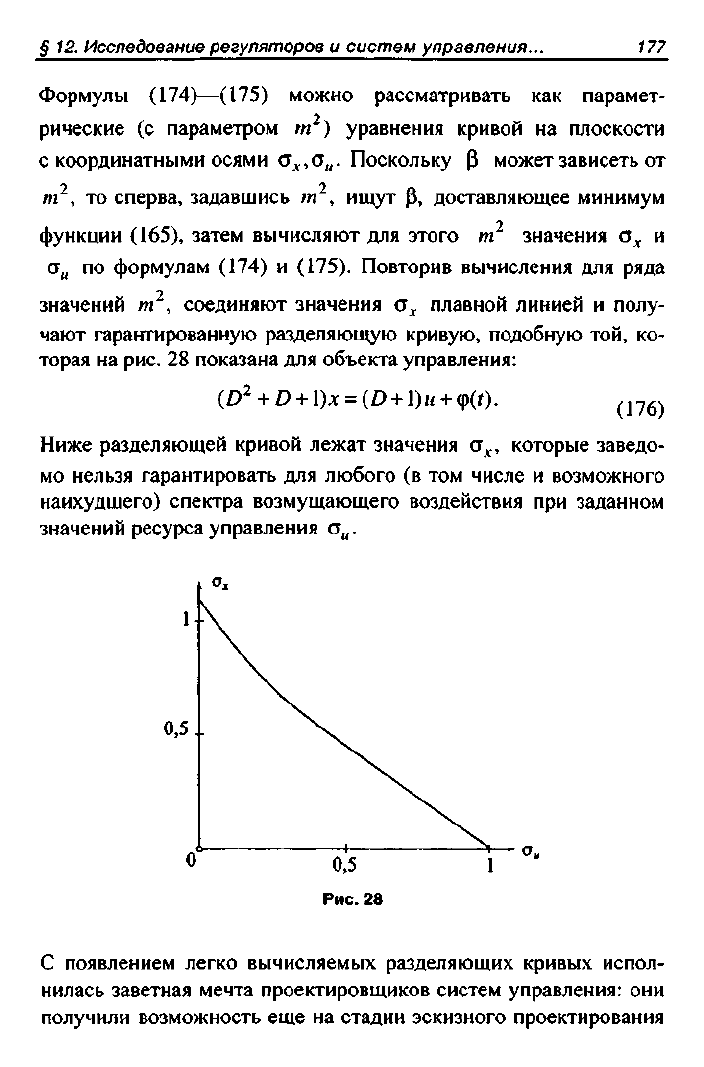
Формулы (174)—(175) можно рассматривать как парамет-

рические (с параметром т ) уравнения кривой на плоскости

с координатными осями о

,с

. Поскольку Р может зависеть от

т , то сперва, задавшись т , ищут (3, доставляющее минимум

функции (165), затем вычисляют для этого т значения а

по формулам (174) и (175). Повторив вычисления для ряда

2 ~

значении т , соединяют значения о

плавной линией и полу-

чают гарантированную разделяющую кривую, подобную той, ко-

торая на

рис.

28 показана для объекта управления:

+ О + 1)х = (О + 1)н +

ф(0.

(1?6)

Ниже разделяющей кривой лежат значения а

, которые заведо-

мо нельзя гарантировать для любого (в том числе и возможного

наихудшего) спектра возмущающего воздействия при заданном

значений ресурса управления ст

Рис. 28

С появлением легко вычисляемых разделяющих кривых испол-

нилась заветная мечта проектировщиков систем управления: они

получили возможность еще на стадии эскизного проектирования

178 §

12.

Исследование регуляторов

систем

управления...

быстро и точно определить, какая точность стабилизации или

слежения достижима при заданном ресурсе управления, или ка-

кой ресурс необходим для достижения заданной точности. При-

меры построения разделяющих кривых для различных объектов

управления были приведены в

[199].

Если в уравнении объекта управления (161) полином А{П) и по-

лином В(й) — гурвицевы полиномы, то разделяющая кривая

начинается (как показано в

[199],

стр. 68) на оси ординат, в точке

=0, о

= Дд(-а.\\> (

Р вычисляется для т

=0) закан-

чивается на оси абсцисс, в точке о

= 0,

= \<

Й(

^л, где Р

вычисляется при т

—»

«.

(эти соотношения справедливы, разу-

меется, для нормированного спектра, при о

более общий

случай, возникающий при оптимизации следящих систем, когда

используемый при расчете оптимального управления спектр мо-

жет не иметь конечного среднего квадрата, был описан в [199] на

стр.

63—66).

Не менее интересно поведение разделяющих кривых для объек-

тов управления (161) с негурвицевыми полиномами А(0) или

5ф) — т. е. для объектов, не устойчивых без управления или не

минимально-фазовых. И здесь, опираясь на формулы, полученные

ранее в [44] и

[195],

удалось получить очень простые решения:

Если объект управления (161) не устойчив без управления,

т. е. полином Аф) имеет хотя бы один положительный ко-

рень а,, то при среднем квадрате управляющего воздействия

меньшем, чем V'. .• ничего гарантировать нельзя, даже

устойчивости замкнутой системы. Разделяющая кривая (вы-

числяемая по-прежнему по формулам (174)—(175), приобре-

тает физический смысл лишь правее абсциссы

_1_

\В(щ)[

0«тт =Г^7-Тг (177)

12.

Исследование регуляторов и систем управления... 179

Если в(О) =

то

ит

т. е. мощность управления должна

быть не меньше мощности (среднего квадрата) возмущающего

воздействия, иначе не будет гарантирована даже устойчивость

замкнутой системы.

Если объект управления (161)' является не минимально-

фазовым, г. е. полином В{В) имеет хотя бы один поло-

жительный корень Р,, то при любом ресурсе управления нельзя

гарантировать значение критерия качества а

меньше, чем

(178)

В разделяющей кривой (по-прежнему вычисляемой по формулам

(174)—(175)) физический смысл имеет та ее часть, которая лежит

выше ординаты (178). Часть разделяющей кривой, лежащую ни-

же ординаты (178), следует заменить на горизонтальную прямую,

проходящую через

хт{п

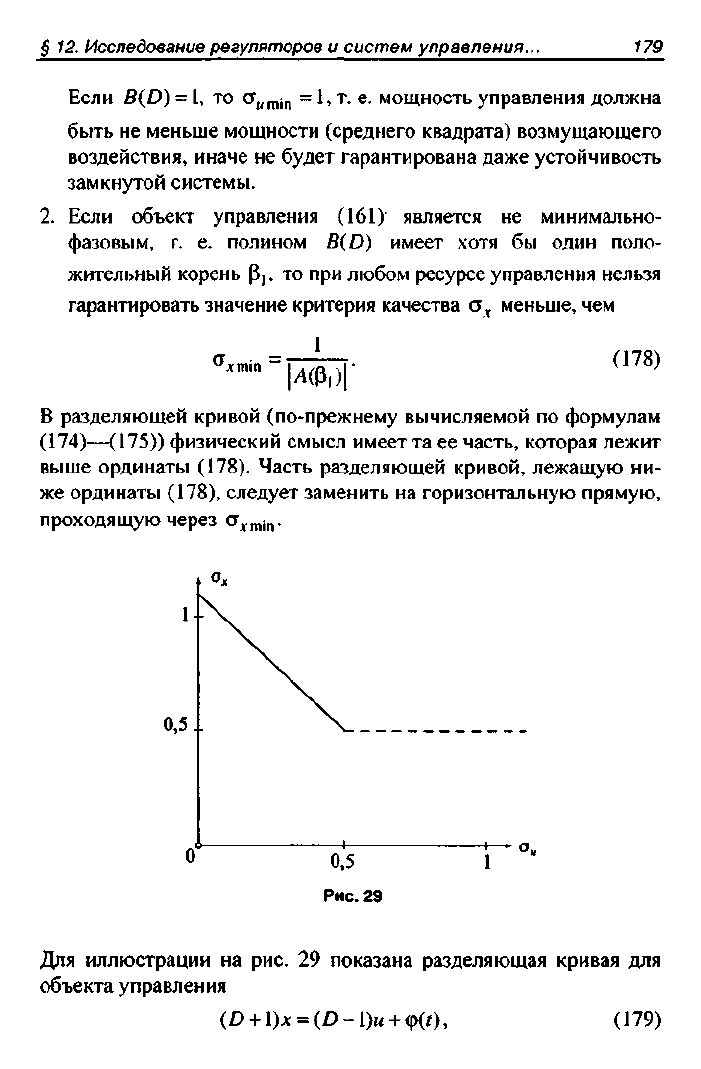
Рис. 29

Для иллюстрации на рис. 29 показана разделяющая кривая для

объекта управления

1)л:

ф-1)и+(р(0, (179)

180 §

12.

Исследование регуляторов

и систем управления...

у которого

=1 и

-. г =

0,5.

Разделяющая кривая заканчива-

ется в точке о

0,5;

0,5.

Справа от этой точки разделяющая

кривая дополнена горизонтальной пунктирной прямой. Значений

0,5

нельзя гарантировать при любом ресурсе управления

. Кстати, на примере объекта управления (179) в учебном по-

собии [195] были разъяснены физический смысл и причина не-

возможности обеспечить для неминимально-фазовых объектов

управления значения о

, меньшие некоторых предельных зна-

чений, зависящих от спектров возмущающих воздействий: при-

чина заключается в том, что для таких объектов действие произ-

водной от управляющего воздействия йи может иметь знак,

обратный знаку воздействия от самого управления и, и они вза-

имно компенсируют друг друга (степень компенсации зависит от

5ф(и>)). На примере объекта управления (179) это особенно ясно

видно. Отсюда и вытекает невозможность обеспечения для неми-

нимально-фазового объекта управления значения а

0 при лю-

бом ресурсе управления и зависимость наименьшего а

от спек-

тра возмущающих воздействий.

В работе

[199],

стр. 90—91 рассмотрены также и особые случаи,

когда вся разделяющая кривая на всем ее протяжении не имеет

физического смысла, и предельные возможности системы управ-

ления вычисляются особо.

Таким образом, подход, разработанный на факультете ПМ-ПУ,

позволил найти для односвязных систем простое и наглядное

решение проблемы гарантирующего управления. Отметим, что

проблему гарантирующего управления можно рассматривать

и как задачу теории дифференциальных игр, ранее рассмотрен-

ных в публикации [2]. Ее можно рассматривать как "игру" конст-

руктора регулятора против природы, которая может "выбрать"

любой спектр возмущающего воздействия, в том числе и наибо-

лее неблагоприятный для конструктора. Материал, изложенный

в публикации [199] (а ранее — в публикациях [192] и [187]), дает

решение этой дифференциальной игры.

12.

Исследование регуляторов

систем

управления...

181

Кроме того, в работе

[187],

а более подробно в

[199],

рассматри-

валась проблема гарантирующего управления при учете помимо

возмущающих воздействий ф(г) еще и погрешностей измерения

и помех в канале обратной связи \|/(0> когда реально измеряе-

мый выход объекта управления у является суммой двух функций:

у = х

+ \|/,

где х не известное нам истинное значение регулируе-

мой переменной, а \|/(г) — погрешности измерения плюс различ-

ные помехи в канале обратной связи, которые чаще всего явля-

ются стационарным случайным процессом со спектром 5^(со) и

средним квадратом а^.

Если в объекте управления (161) обратная связь разомкнута, т. е.

и=0, то в разомкнутой системе (если, конечно, она устойчива

без управления), будет

ОО 7

^=<^

= .К(со)- ^~а (

180

о \А(Щ

— т. е. значение среднего квадрата регулируемой переменной

в разомкнутой системе о зависит от спектра возмущающего

воздействия 5

и от полинома Д(О). Величина среднего квадра-

та ст

разомкнутой системы будет максимальной при спектре

(со) = 8(со-Р), (181)

где на этот раз Р — частота, при которой достигает минимума

функция |А(у'со)| — модуль частотной характеристики объекта

управления, и максимальное значение о~„ равно:

°>™=\Ш\

<182)

(для нормированного спектра

ц>(1),

т. е. при а

= 1).

Далее в публикации

[199],

стр. 95—98 вычислялся наиболее не-

благоприятный спектр возмущающего воздействия, синтезиро-

182 §

12.

Исследование регуляторов

систем

управления...

вался гарантирующий регулятор и вычислялось гарантированное

значение критерия качества а

. Были получены две формулы:

(183)

184)

для значений среднего квадрата о

х(1) регулируемой перемен-

ной х(1) на выходе объекта управления.

Формула (183) соответствовала тому случаю, когда спектр воз-

мущающего воздействия не совпадал с наихудшим спектром

(181),

и средний квадрат выхода разомкнутой системы вычислял-

ся по формуле (180), а формула (184) соответствовала наиболее

неблагоприятному сочетанию спектров возмущающего воздейст-

вия и погрешности измерений.

На языке теории игр формула (183) дает "цену игры" конструкто-

ра регулятора против природы, которая может выбрать наиболее

неблагоприятный спектр погрешностей измерений, а формула

(184) даст "цену коалиционной игры", когда два "игрока", из ко-

торых один распоряжается спектром ф(0» а другой — спектром

\|/(0 — могут "вступать в коалицию" против "третьего игрока" —

конструктора регулятора.

Как известно, в дифференциальных играх очень редко удается по-

лучить цену игры в замкнутой форме, в виде конечной формулы,

а не сложного алгоритма. Простые формулы (183) и (184) расши-

ряют небольшой список дифференциальных

игр,

для которых уда-

лось получить решение в замкнутой форме. Примеры построения

гарантирующих регуляторов приведены в

[199],

стр.

99—102.

На этом мы заканчиваем изложение исследований по пяти на-

правлениям теории автоматического управления и регулирова-

ния, выполненным в 1969—1999 гг. на факультете ПМ-ПУ под

руководством проф. Петрова Ю. П. В этих исследованиях неоце-

12.

Исследование регуляторов

систем

управления... 183

нимую помощь оказали его аспиранты и докторанты, часть из

которых осталась на факультете и преподают там. Другие поки-

нули факультет, но все они уже давно работают самостоятельно и

не без успеха. В настоящих "Очерках" уже упоминалось о рабо-

тах Е. И. Веремея (ныне заведующий одной из кафедр факультета

ПМ-ПУ), В. В. Еремеева, М. А. Галактионова (доценты). Н. Д. Аб-

дуллаева (впоследствии зав. кафедрой в Баку), И. Н. Марусевой

(впоследствии зав. кафедрой), Ф. П. Рассказова (впоследствии

зав.

кафедрой), В. В. Червякова (впоследствии главный инженер

НПО "Воле"), Ю. Н. Корнилова, Т. Г. Кузьминой (впоследствии

директор института), В. Ф. Шумилова, С. А. Лапкина, Г. С. Дани-

ленко, В. А. Сиверина, М. В. Пассовой, С. С. Новогран, Д. Г. Крас-

ноперовой, Д. Б. Фроленкова. Их публикации отражены в списке

литературы в конце настоящих "Очерков", а более мелкие статьи —

в списках литературы в книгах

[187], [192], [194], [195],

1198],

[199].

Обзор исследований, выполненных до 1981 г., был опубликован

в обзорной статье: Петров Ю. П. "Синтез устойчивых систем

управления, оптимальных по среднеквадратичным критериям

качества". Автоматика и телемеханика, 1983, № 7, стр. 15—24.