Петров Ю.П. Очерки истории теории управления

Подождите немного. Документ загружается.

12.

Исследование регуляторов и систем управления... 145

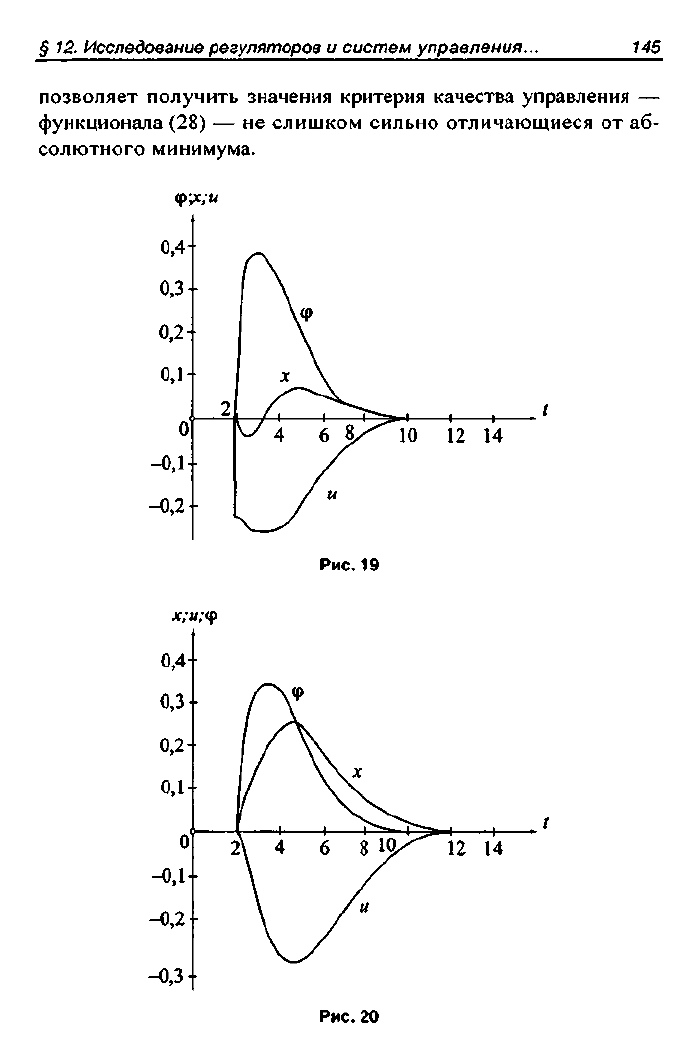
позволяет получить значения критерия качества управления —

функционала (28) — не слишком сильно отличающиеся от аб-

солютного минимума.

Рис. 19

Рис. 20

146 §

12.

Исследование регуляторов

и систем управления...

Для сравнения на рис. 20 показаны значения управляющего

воздействия

и(1)

и отклонения х(1) для того же возмущающего

воздействия (133), что и на рис. 18 и 19, но реализуемые регу-

лятором, построенным на основе методики аналитического

конструирования, которая не использует предсказания будущих

значений возмущающего воздействия. Рис. 20 наглядно показы-

вает, что отказ от предсказания увеличивает х(() и и(() по

сравнению с регулятором, построенным на основе корреляци-

онной теории случайных процессов, и увеличивает тем самым

значение критерия качества управления — функционала (28).

Заметим, что "аналитическое конструирование" регуляторов

предназначалось первоначально А. М. Лётовым для объектов

управления без возмущающих воздействий; затем оно стало

часто использоваться для объектов, подверженных влиянию не

полностью известных возмущающих сил случайного характера;

понятно, что в этих новых условиях оно оказалось не опти-

мальным.

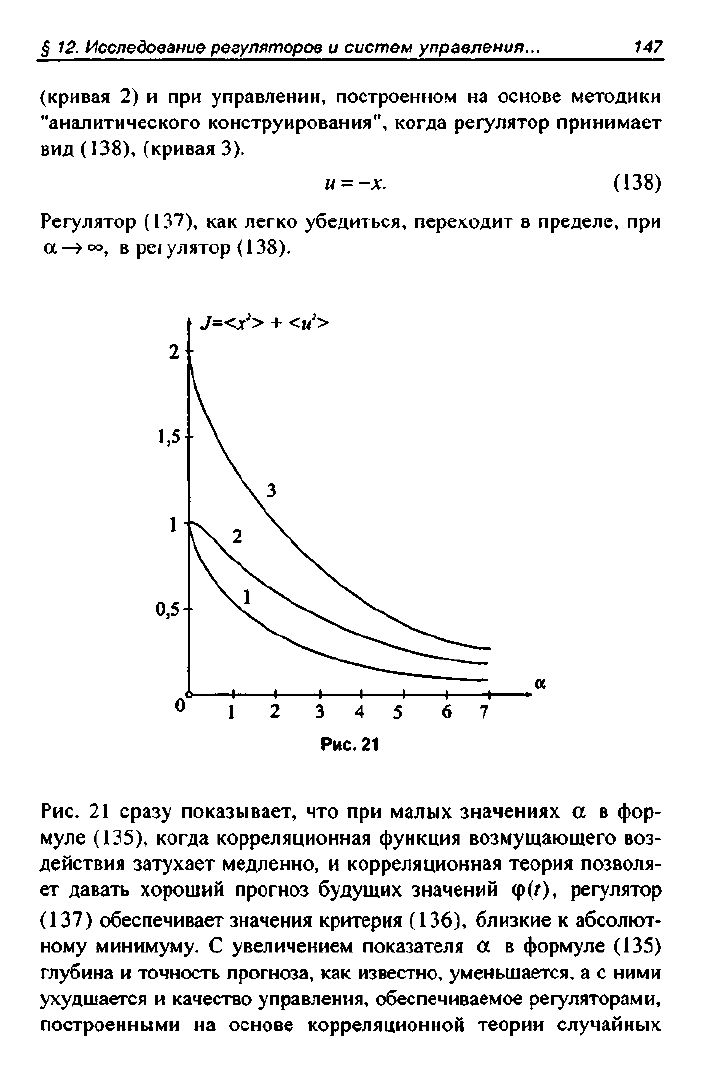
На рис. 21, ранее опубликованном в

[192],

для простейшего объ-

екта управления:

= и + (р(0

(134)

при возмущающем воздействии с корреляционной функцией

для различных значений а сопоставлены значения критерия

качества

/=7л

<л:

<н

> (136)

(для т

= 1)

при оптимальном программном управлении (кривая 1,

абсолютный минимум), при управлении с обратной связью, по-

строенной на основе корреляционной теории случайных процес-

сов,

когда регулятор имеет вид

и =-

(\ 1 "I

-0 + -

+ 1

\<х о. )

(137)

12.

Исследование регуляторов

систем

управления...

147

(кривая 2) и при управлении, построенном на основе методики

"аналитического конструирования", когда регулятор принимает

вид (138), (кривая 3).

-х. (138)

Регулятор (137), как легко убедиться, переходит в пределе, при

а—»°о, в ре1улятор (138).

°" 1 2 3 4 5 6 7

Рис. 21

Рис.

21 сразу показывает, что при малых значениях а в фор-

муле (135), когда корреляционная функция возмущающего воз-

действия затухает медленно, и корреляционная теория позволя-

ет давать хороший прогноз будущих значений ф(0, регулятор

(137) обеспечивает значения критерия (136), близкие к абсолют-

ному минимуму. С увеличением показателя а в формуле (135)

глубина и точность прогноза, как известно, уменьшается, а с ними

ухудшается и качество управления, обеспечиваемое регуляторами,

построенными на основе корреляционной теории случайных

148 §

12.

Исследование регуляторов

и систем управления...

процессов. Основа эффективности этих регуляторов заключается

в использовании частичного предсказания будущих значений слу-

чайного процесса ф(0 — предсказания частичного, не полного,

но зато совместимого с устойчивостью.

Эффективность частичного предсказания зависит, разумеется, от

конкретных характеристик объектов управления. Анализ эффек-

тивности для морских судов был проведен в

[192],

стр. 139. Ока-

залось, что частичное предсказание обеспечивает для различных

судов значения критерия качества (136) в 2,6, в 3,3 раза хуже аб-

солютного минимума. Отсюда следовал совет проектантам сис-

тем управления: если есть возможность лучшего предсказания,

используйте,ее! Что касается методики "аналитического конст-

руирования" регуляторов, то она полностью отказывается от ис-

пользования предсказания будущих значений возмущающего

воздействия, но зато приводит к более простым регуляторам

(регулятор (138) является пределом регуляторов вида (137) при

а->«>).

Мы остановились столь подробно на физическом смысле опти-

мального управления (ранее изложенного в публикациях [192]

и [187]) потому, что во всех последующих многочисленных пуб-

ликациях по оптимальному управлению линейными системами

разъяснению физического смысла, объяснению причин его эф-

фективности (или, в ряде случаев, его малой эффективности) уде-

лялось незаслуженно мало внимания. Читатель этих публикаций

знакомился с многочисленными алгоритмами синтеза оптималь-

ных регуляторов, с примерами численного расчета, но причина

эффективности (или неэффективности) управления, основанного

на корреляционной теории, оставалась не разъясненной. Упуска-

лось из вида, что в автоматическом управлении главное — это не

цифры, а понимание.

Исследования линейных оптимальных систем на факультете

ПМ-ПУ СПбГУ во многом шли параллельно исследовательской

работе других научных центров. Истина одна — и открывалась

она почти одновременно различным группам исследователей.

Так, поведение корней характеристического полинома опти-

мальных систем при увеличении среднего квадрата управляю-

12.

Исследование регуляторов

систем

управления...

749

щего воздействия и коэффициентов усиления регулятора публи-

ковалось как в книгах

[192],

стр. 168—170, в

[187],

стр. 229—232,

так и в книге [ПО]. Независимо полученные в этих работах ре-

зультаты, как и следовало ожидать, совпали.

Точно так же результаты исследования предельных возможно-

стей неминимально-фазовых объектов управления — т. е. объек-

тов,

в математической модели которых

Л(0)*

Д(0)и

+ ф(О

(139)

операторный полином Вф) при управляющем воздействии не

является гурвицевым и имеет корни в правой полуплоскости

комплексного переменного, печатались и в Ленинграде [44],

[195],

стр. 89—94, и в Киеве

[172],

стр. 39—40. И там и тут

было установлено, что в неминимально-фазовой системе (в от-

личие от минимально-фазовой) существует предельное наимень-

шее значение функционала (х )— среднего квадрата регули-

руемой величины — которое нельзя уменьшить никаким увели-

чением управляющего воздействия, никаким увеличением ко-

эффициентов усиления регулятора.

Результаты, полученные на факультете ПМ-ПУ и опубликован-

ные в [44] и в

[195],

стр. 82—94, были более подробны. Они

включали в себя простую формулу для наименьшего возможно-

го значения среднего квадрата регулируемой переменной (х

)

в неминимально-фазовой системе:

где

5^0'со)

— результат факторизации спектра возмущающего

воздействия 5^,(0)), т. е. результат его разложения на симметрич-

ные множители:

(со)

= 5,(7(0)-5,

(-;со),

а Р, — правый корень полинома В(О) в математической модели

объекта управления (139). Формула (140) справедлива для поли-

(140)

150 §

12.

Исследование регуляторов

и систем управления...

номов Вф), имеющих один вещественный положительный ко-

рень.

Формула (140) интересна тем, что она проявила совершен-

но неожиданные зависимости (х

) от параметров объекта

управления (139) — зависимости, которых интуитивно никак

нельзя было ожидать. Кроме того, эта формула помогла потом

решить проблему гарантирующего управления при неизвестном

возмущающем воздействии; о ней мы расскажем далее.

Любопытно отметить, что в ходе исследования были обнару-

жены совершенно экзотические объекты управления, для кото-

рых любое управляющее воздействие, отличное от и

= 0,

ухуд-

шает среднеквадратичный критерий качества. Оптимальное

управляющее воздействие для таких экзотических объектов —

это

и = 0.

Более подробно такие объекты рассмотрены в

[195],

стр.

91.

В публикации [195] было приведено также решение известного

парадокса теории управления: с одной стороны, еще Р. Калман

в 1960 г. доказал, что у всех управляемых по Калману объектов

(в том числе и неминимально-фазовых — лишь бы они были

управляемы по Калману) достижимо любое, сколь угодно малое

время перехода из одной точки фазового пространства в другую,

достижима любая скорость затухания переходных процессов,

лишь бы управляющее воздействие было достаточно велико. Как

совместить эти строго доказанные результаты с тем, что при

любом управляющем воздействии величина (х ) не может

быть сделана меньше, чем (х

) ?

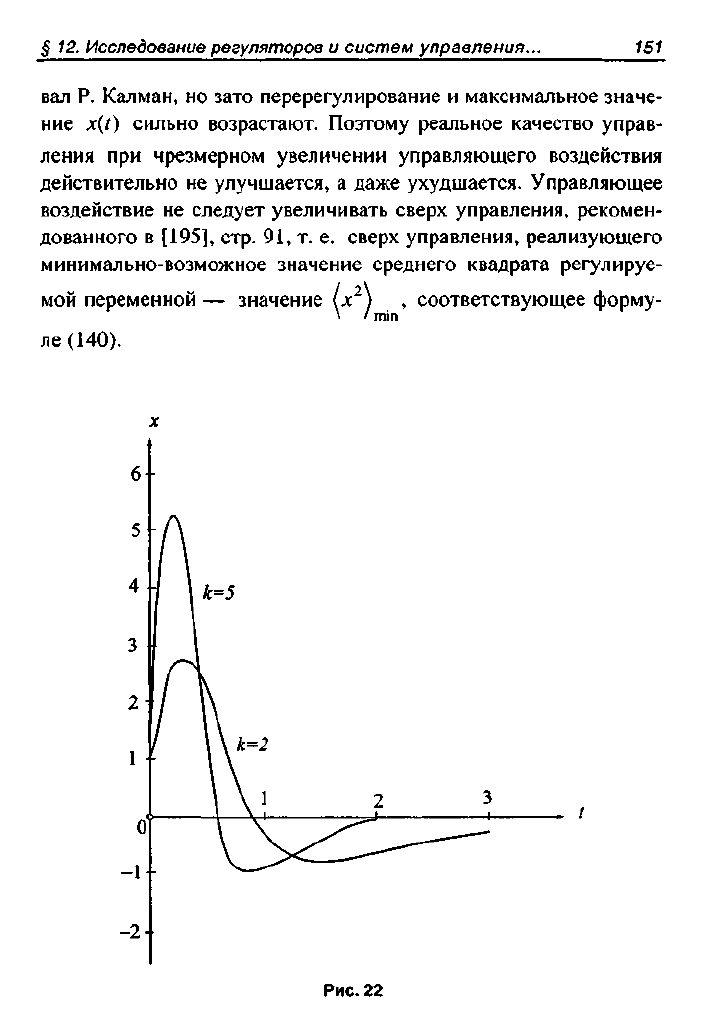
Прямое вычисление и построение переходных процессов при

различных коэффициентах усиления, результаты которого при-

ведены на рис. 22, а ранее были опубликованы в

[195],

стр.

123, показало, что противоречия на самом деле нет: при

увеличении управляющего воздействия (переход отк

2кк=5

на рис. 22) переходный процесс в неминимально-фазовом объек-

те управления действительно затухает быстрее, как и предсказы-

12.

Исследование регуляторов и систем управления... 151

вал Р. Калман, но зато перерегулирование и максимальное значе-

ние х(1) сильно возрастают. Поэтому реальное качество управ-

ления при чрезмерном увеличении управляющего воздействия

действительно не улучшается, а даже ухудшается. Управляющее

воздействие не следует увеличивать сверх управления, рекомен-

дованного в

[195],

стр. 91, т. е. сверх управления, реализующего

минимально-возможное значение среднего квадрата регулируе-

мой переменной — значение (х ) , соответствующее форму-

\ ' 1ТИП

ле (140).

Рис. 22

152 §

12.

Исследование регуляторов

и систем управления...

Улучшение в понимании физического смысла оптимального

управления позволило более успешно решать на факультете ПМ-

ПУ самые различные задачи оптимизации. В § 5 уже были опи-

саны успешные решения сотрудниками факультета ПМ-ПУ ряда

относительно стандартных задач оптимизации — задач обеспе-

чения минимума среднего квадрата регулируемой величины при

тех или иных ограничениях на управление. Приходилось иметь

дело и с нестандартными задачами. Характерным примером мо-

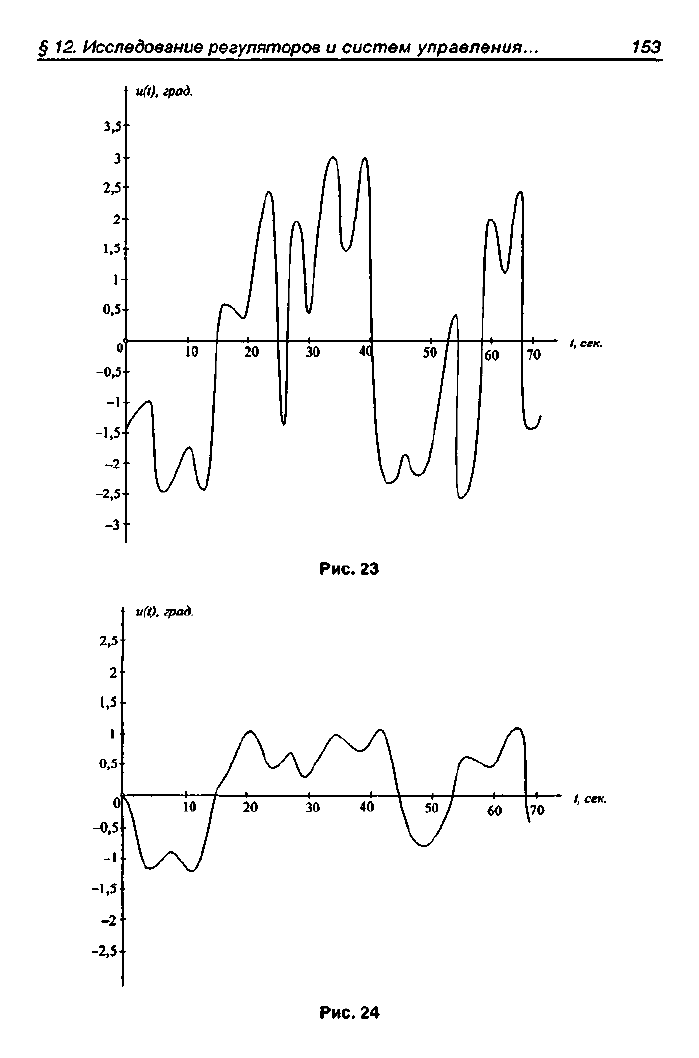
жет служить опубликованное в [43] решение интересной и важ-

ной для практики судовождения задачи о минимуме числа пере-

кладок руля. Традиционные авторулевые обеспечивали хорошее

удержание судна на курсе, но в штормовых условиях они сильно

изнашивали рулевую установку — число перекладок руля дости-

гало 350—400 в час. Встал вопрос: нельзя ли при том же качестве

удержания на курсе уменьшить число перекладок? Оказалось,

что при новой структуре регулятора, отличной от традиционной,

но отнюдь не более сложной, чем традиционная, достижимо

значительное облегчение условий работы (а тем самым и увели-

чение долговечности) рулевой установки. Среднее число пере-

кладок в час удалось сократить в

4—5

раз. На рис. 23 показаны

повороты руля

(0 в функции времени при регуляторе традици-

онной структуры, а на рис. 24 — при регуляторе, спроектирован-

ном по методике статьи [43].

Математическая модель этого регулятора имела вид:

(141)

где 9 — отклонение судна от заданного курса в градусах. Эф-

фект от оптимизации управления сразу виден.

Более подробно вывод оптимального закона управления и реали-

зация регулятора (141) описаны в монографии [1], стр. 222—225.

Решения многих проблем, возникающих при проектировании и

оптимизации систем управления стабилизацией и динамическим

позиционированием буровых судов, ведущих разведку и добычу

полезных ископаемых с морского дна, были опубликованы в мо-

нографии

[194].

12.

Исследование регуляторов и систем

управления...

153

Рис.

154 §

12.

Исследование регуляторов

и систем управления...

12.3.

Обеспечение комплекса

требований к системе управления

В предыдущих разделах были отражены результаты исследо-

ваний, в которых сотрудники факультета ПМ-ПУ шли, в об-

щем и целом, в параллельных направлениях с другими научными

школами, исследуя свойства и особенности оптимальных систем

и оптимизируя конкретные объекты управления.

Направление исследований, о котором мы расскажем в настоя-

щем разделе, до 1984 г. велось практически только на факуль-

тете ПМ-ПУ. Это — обеспечение комплекса требований к системе

управления, в основном за счет изменения аналитической аппрок-

симации экспериментальных данных по спектрам возмущающих

воздействий. Важность этого направления исследований дру-

гими научными школами недооценивалась, хотя всем было ясно,

что обеспечение минимума среднеквадратичного критерия качест-

ва еще совершенно недостаточно для успешной работы реаль-

ных систем управления, которые должны удовлетворять целому

комплексу технических требований.

Возникла идея: обеспечить удовлетворение дополнительных тех-

нических требований за счет изменения аналитической аппрок-

симации спектра. Было известно, что спектр возмущающих воз-

действий получается из эксперимента в виде набора точек для

ряда значений частоты, и эти точки можно аппроксимировать

четными рациональными дробями вида

(142)

с различными значениями р и ц.

В 1974—1976 гг. автором настоящих "Очерков" совместно с

Е.

И.

Ве-

ремеем и

С.

Н. Андриановым были проанализированы степени опера-

торных

полиномов Щ (О)

и Щ(О)

оптимальных регуляторах

(143)