Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

Preliminary data processing and phase analysis

361

Overall, up to five parameters per diffraction peak can be refined: 28,

and

(or

q).

order to proceed with profile fitting using non-linear

least squares refinement, all parameters should be assigned reasonable initial

values. This is usually achieved in the following way:

Approximate peak positions can be obtained using visual localization, or

from the automatic peak search, or they may be calculated from unit cell

dimensions, if the latter are known.

Approximate peak shape parameters can be preset to some practical or

default values. They may be visually estimated from the pattern (the

easiest is the full width at half maximum) andlor determined from a

single, well resolved strong Bragg peak.

Approximate integrated intensity is easily established automatically:

when only "scale factors" of individual peak shapes are of concern, a

linear least squares technique can be employed to find them relatively

precisely (see Chapter 5, section

5.13.1 for a description of the method

and Eq. 2.48 in Chapter 2, which indicates that the governing equations

are indeed linear with respect to

I).

All initial parameters can be approximate but they should be sufficiently

precise to ensure that the non-linear least squares minimization converges.

Approximate peak positions are among the most important, and they should

fall within the range of each peak, or better yet, in the range of their full

widths at half maximum. Usually this relatively vague localization of Bragg

reflections is not a problem even when peak tops are chosen to represent

initial peak positions. However, when processing clusters of Bragg

reflections with considerable overlapping, the approximate peak locations

should be as precise as possible to ensure the stability of the least squares

minimization.

Depending on the quality of the pattern, profile fitting can be conducted

in several different ways. They differ in how peak positions and peak shape

parameters are handled, assuming that integrated intensities are always

refined independently for each peak, and a single set of parameters describes

a background within the processed range:

1. All possible variables (positions and shapes) are refined independently

for each peak or with some constraints. For example, an asymmetry

parameter is usually a variable, common for all peaks; full width at half

maximum or even all peak shape function parameters may be common

for all peaks, especially if a relatively narrow range of Bragg angles is

processed. When justified by the quality of data, an independent fit of all

or most parameters produces best results. A major problem in this

approach

(i.e. all parameters are free and unconstrained) occurs when

clusters of reflections include both strong and weak Bragg peaks. Then,

peak shape parameters corresponding to weak Bragg peaks may become

3 62

Chapter

unreasonable. Furthermore, when several strong reflections heavily

overlap (typically, when the difference in peak positions is only a small

fraction of the full width at half maximum), their positions and especially

integrated intensities strongly correlate. As a result, a non linear least

squares minimization may become unstable.

2. Positions of Bragg peaks are refined independently but the peak shape

function parameters except asymmetry, which is usually identical for all

peaks, are treated as corresponding functions of Bragg angle (see Chapter

2, section 2.9.1, Eqs. 2.49 to 2.52 and the following explanations). A

major benefit of this approach is a more stable refinement of both the

positions and intensities of weak Bragg peaks when they are randomly

intermixed with strong reflections. A major drawback is its inability to

correctly determine peak shape parameters when only weak peaks are

present in the region included in the processing, or when a few strong

peaks are grouped together, thus preventing a stable determination of

relevant nonlinear dependencies over a broad range of Bragg angles.

3. Peak locations are defined by lattice parameters, which are refined, while

peak positions are calculated using Eqs. 2.29 to 2.37 (see Chapter 2,

section 2.8). Peak shape parameters are handled as described in item 2,

above, and rarely as in item

This approach is possible only when unit

cell dimensions are known at least approximately. Therefore, this is no

longer an unbiased preliminary data processing but it rather becomes a

full pattern decomposition using

Pawley or Le Bail methods, which are

discussed later (Chapter

6).

This refinement is often used to obtain

accurate lattice parameters without employing other structural details.

major benefit here is relatively precise integrated intensities, which are

usable for solving the crystal structure from first principles (see Chapter

2, section 2.14). A major drawback is that any full pattern decomposition

approach requires knowledge of the lattice parameters and symmetry, and

therefore, is unsuitable for an unbiased determination of both the

positions and integrated intensities of Bragg reflections.

Examples of profile fitting shown below were obtained using the

DMSNT software. It employs two peak shape functions: the Pearson-VII for

symmetric peaks and the split Pearson-VII to treat the asymmetric peaks. All

peak shape parameters can be refined independently; all or any of them can

be fixed. There is no mechanism to constrain peak shape parameters,

e.g. to

make some or all of them common for several peaks, or to treat them as

corresponding functions of 28. Therefore, in many cases when substantial

peak overlapping is observed,

and/or when data are of relatively low quality

and resolution, profile fitting becomes unstable and does not converge.

Moreover, background must be subtracted prior to profile fitting, as its

refinement is not implemented and, therefore, not allowed.

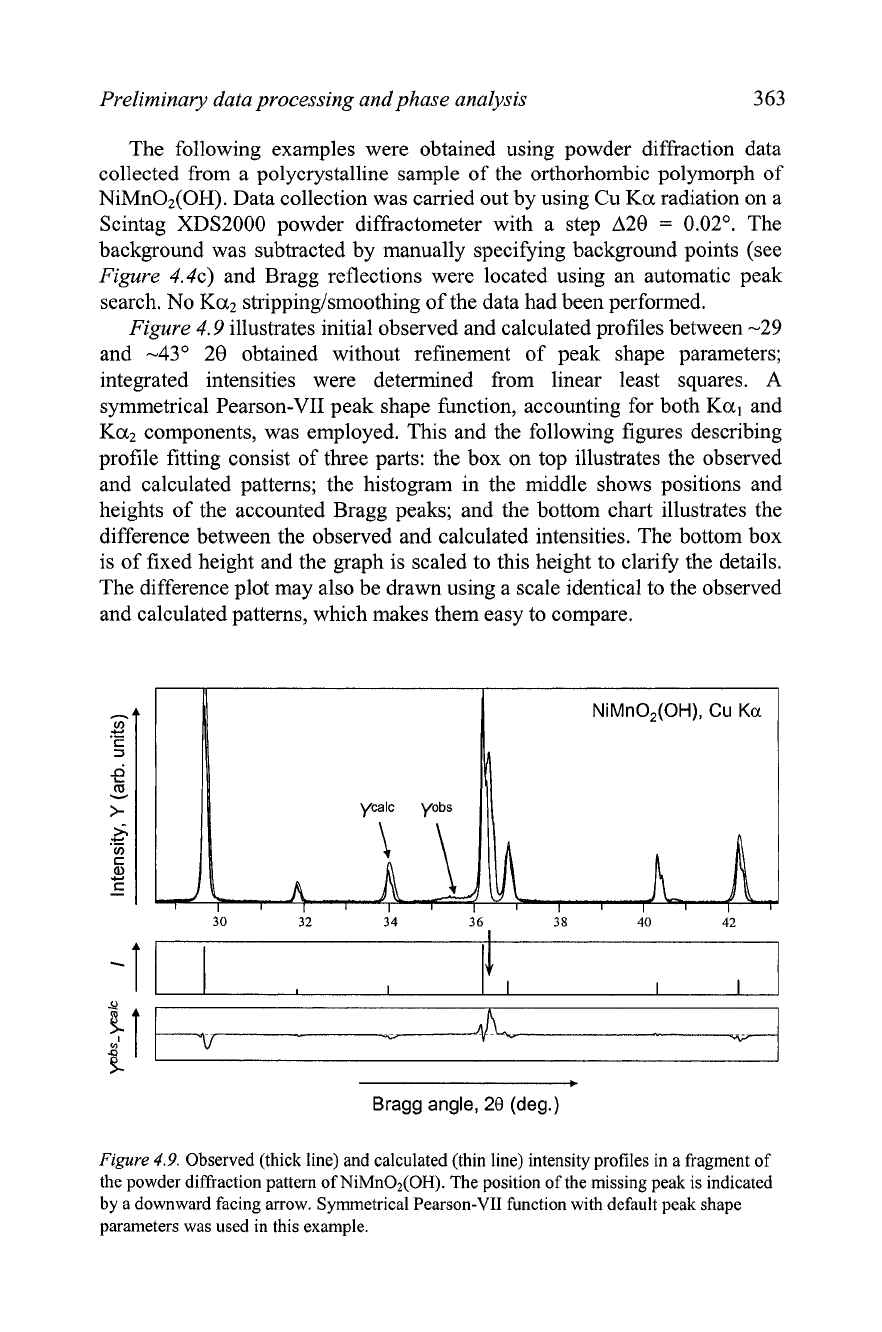
Preliminary data processing and phase analysis

3 63

The following examples were obtained using powder diffraction data

collected from a polycrystalline sample of the orthorhombic polymorph of

NiMn02(OH). Data collection was carried out by using Cu Ka radiation on a

Scintag XDS2000 powder diffiactometer with a step A20

0.02". The

background was subtracted by manually specifying background points (see

Figure

4.4~) and Bragg reflections were located using an automatic peak

search. No Ka2 strippinglsmoothing of the data had been performed.

Figure

4.9 illustrates initial observed and calculated profiles between -29

and -43" 28 obtained without refinement of peak shape parameters;

integrated intensities were determined from linear least squares.

symmetrical Pearson-VII peak shape function, accounting for both Kal and

Ka2 components, was employed. This and the following figures describing

profile fitting consist of three parts: the box on top illustrates the observed

and calculated patterns; the histogram in the middle shows positions and

heights of the accounted Bragg peaks; and the bottom chart illustrates the

difference between the observed and calculated intensities. The bottom box

is of fixed height and the graph is scaled to this height to clarify the details.

The difference plot may also be drawn using a scale identical to the observed

and calculated patterns, which makes them easy to compare.

Bragg angle,

(deg.)

Figure

4.9.

Observed (thick line) and calculated (thin line) intensity profiles in a fragment of

the powder diffraction pattern of NiMn02(0H). The position of the missing peak is indicated

by a downward facing arrow. Symmetrical Pearson-VII function with default peak shape

parameters was used in this example.

3 64

Chapter

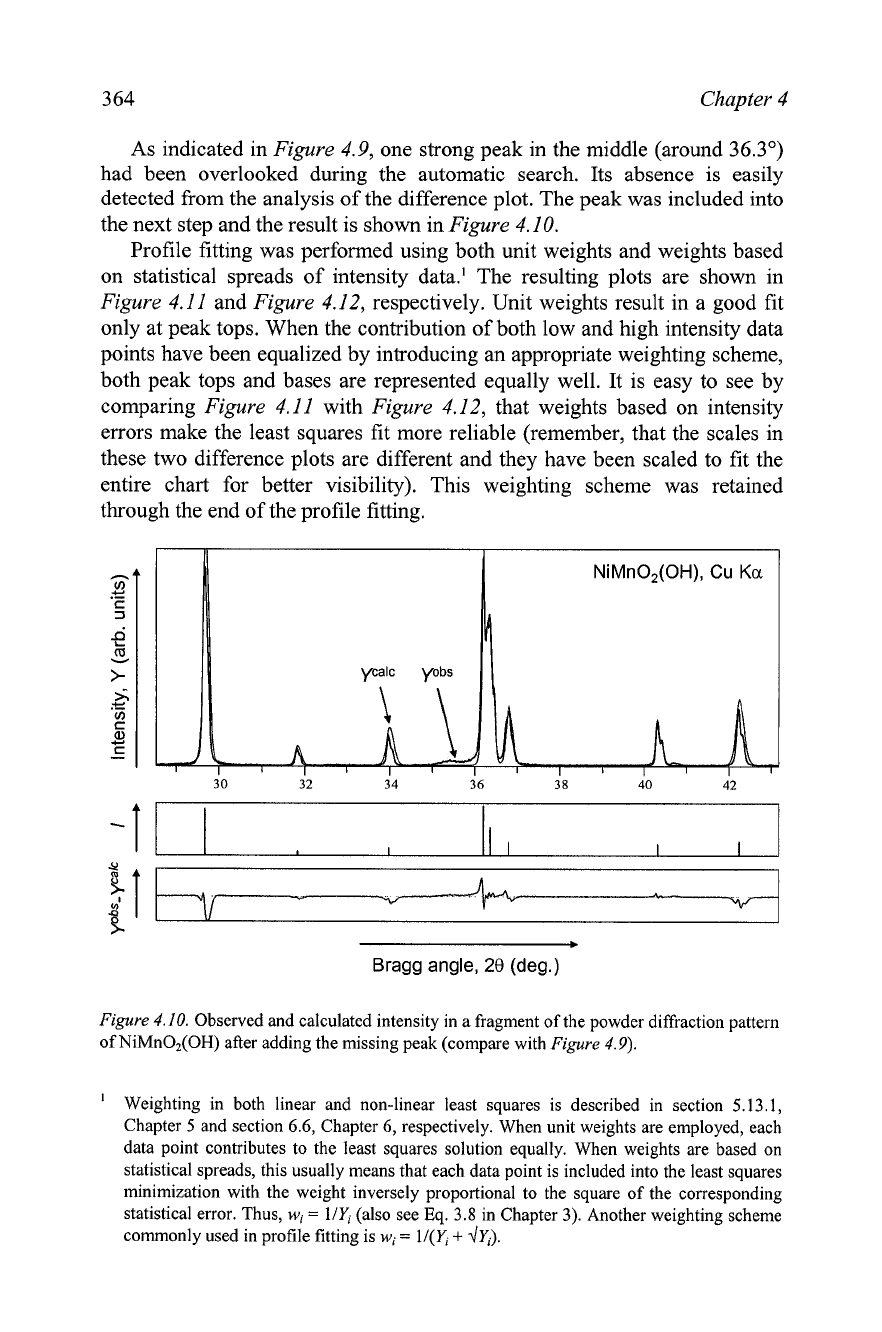
As indicated in

Figure

4.9, one strong peak in the middle (around 36.3')

had been overlooked during the automatic search. Its absence is easily

detected from the analysis of the difference plot. The peak was included into

the next step and the result is shown in

Figure

4.10.

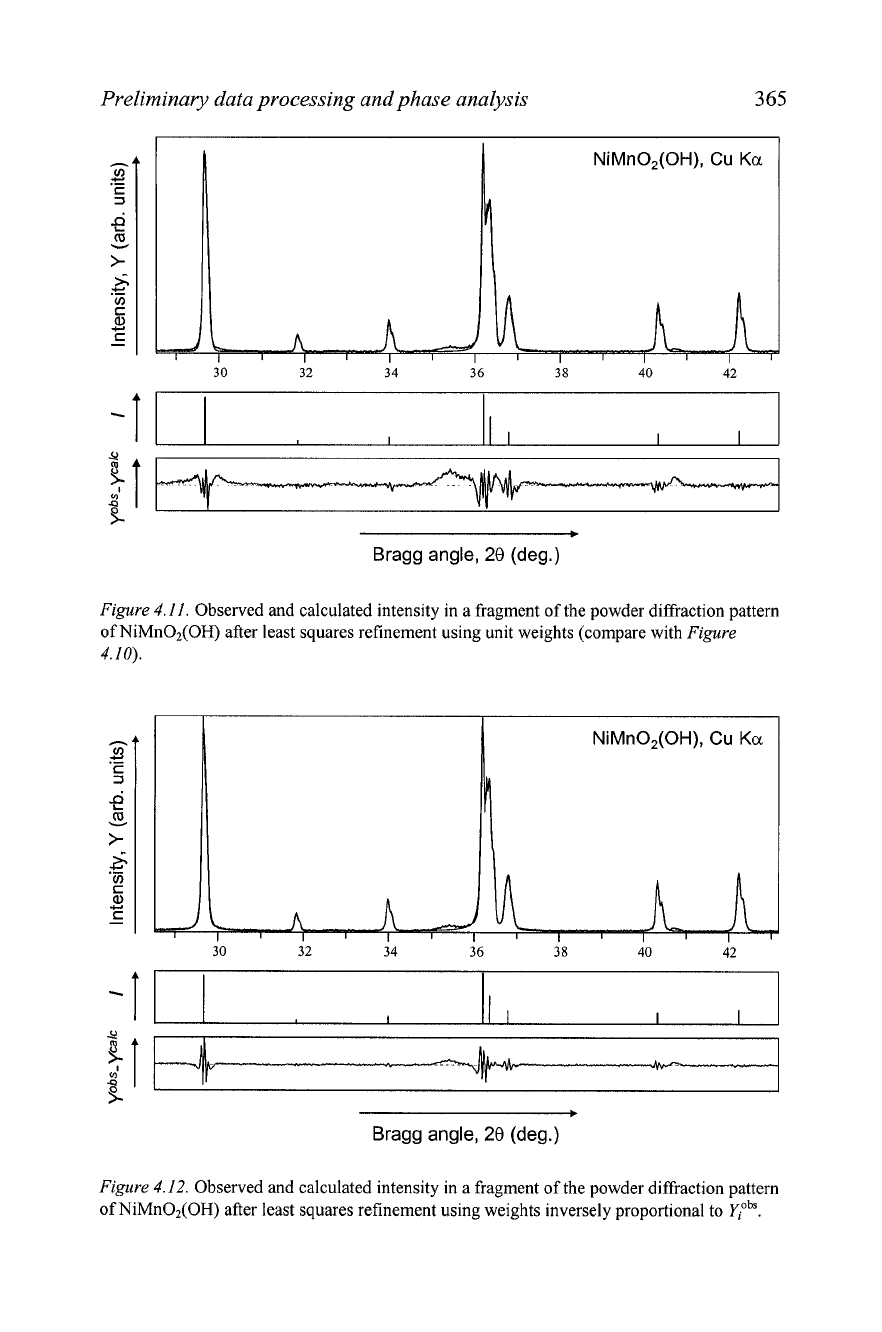
Profile fitting was performed using both unit weights and weights based

on statistical spreads of intensity data.' The resulting plots are shown in

Figure

4.11 and

Figure

4.12, respectively. Unit weights result in a good fit

only at peak tops. When the contribution of both low and high intensity data

points have been equalized by introducing an appropriate weighting scheme,

both peak tops and bases are represented equally well. It is easy to see by

comparing

Figure

4.11 with

Figure

4.12, that weights based on intensity

errors make the least squares fit more reliable (remember, that the scales in

these two difference plots are different and they have been scaled to fit the

entire chart for better visibility). This weighting scheme was retained

through the end of the profile fitting.

Bragg angle,

(deg.)

Figure

4.10.

Observed and calculated intensity in a fragment of the powder diffraction pattern

of NiMn02(OH) after adding the missing peak (compare with

Figure

4.9).

Weighting in both linear and non-linear least squares is described in section

5.13.1,

Chapter

and section

6.6,

Chapter

respectively. When unit weights are employed, each

data point contributes to the least squares solution equally. When weights are based on

statistical spreads, this usually means that each data point is included into the least squares

minimization with the weight inversely proportional to the square of the corresponding

statistical error. Thus,

14 (also see Eq. 3.8 in Chapter

3).

Another weighting scheme

commonly used in profile fitting is

1/(K

d~).

Preliminary data processing and phase analysis

365

Bragg angle,

(deg.)

Figure

4.11.

Observed and calculated intensity in a fragment of the powder diffraction pattern

of NiMn02(OH) after least squares refinement using unit weights (compare with

Figure

4.10).

Bragg angle,

(deg.)

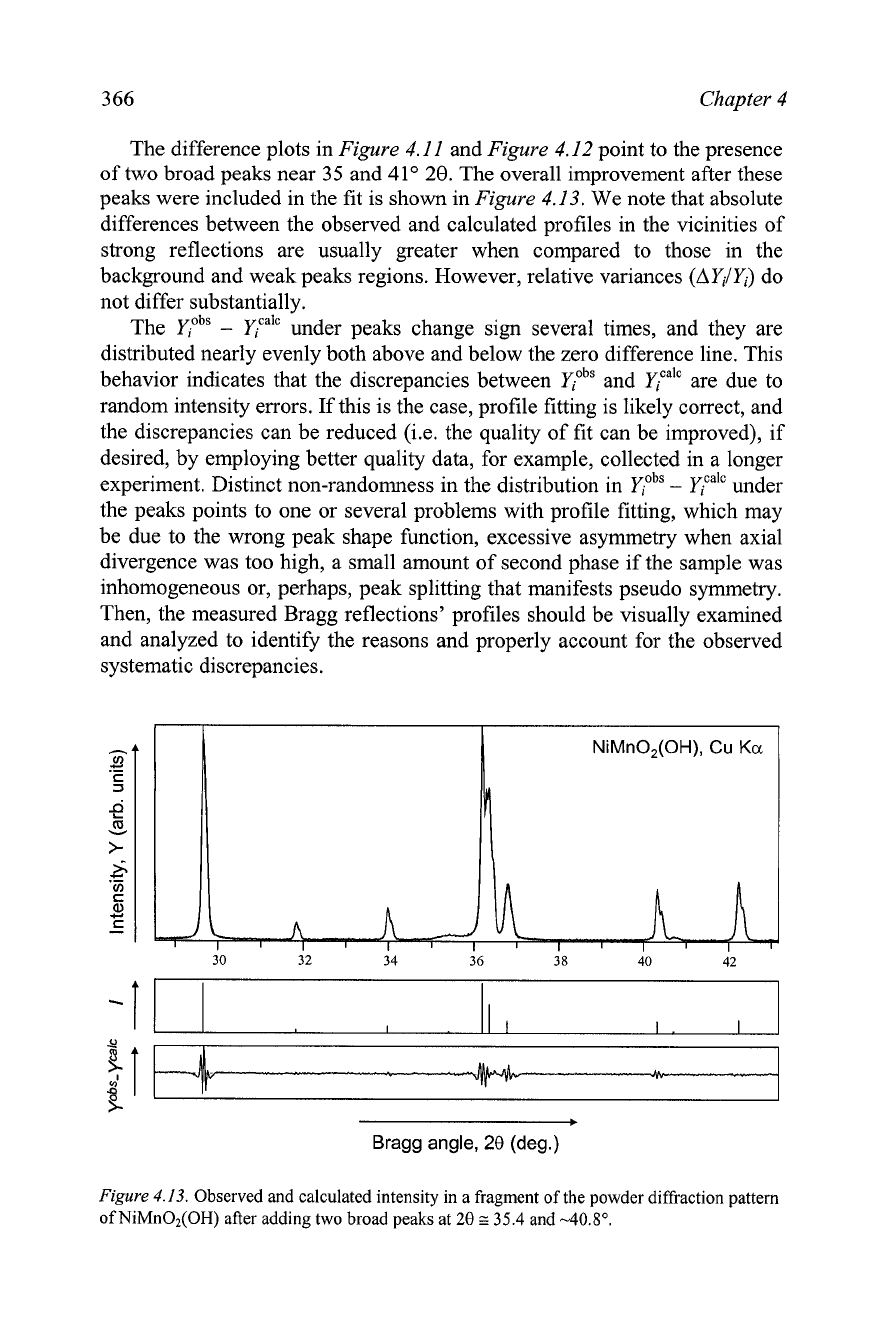
Figure

4.12.

Observed and calculated intensity in a fragment of the powder diffraction pattern

of NiMnO,(OH) after least squares refinement using weights inversely proportional to

yiobs.

Chapter

The difference plots in

Figure

4.11

and

Figure

4.12

point to the presence

of two broad peaks near

and

41"

20.

The overall improvement after these

peaks were included in the fit is shown in

Figure

4.13.

We note that absolute

differences between the observed and calculated profiles in the vicinities of

strong reflections are usually greater when compared to those in the

background and weak peaks regions. However, relative variances

(AYi/&)

not differ substantially.

The

yiob"

under peaks change sign several times, and they are

distributed nearly evenly both above and below the zero difference line. This

behavior indicates that the discrepancies between

yiObS

and

Fa''

are due to

random intensity errors. If this is the case, profile fitting is likely correct, and

the discrepancies can be reduced (i.e. the quality of fit can be improved), if

desired, by employing better quality data, for example, collected in a longer

experiment. Distinct non-randomness in the distribution in

yiObS

ylcalc

under

the peaks points to one or several problems with profile fitting, which may

be due to the wrong peak shape function, excessive asymmetry when axial

divergence was too high, a small amount of second phase if the sample was

inhomogeneous or, perhaps, peak splitting that manifests pseudo symmetry.

Then, the measured Bragg reflections' profiles should be visually examined

and analyzed to identify the reasons and properly account for the observed

systematic discrepancies.

Bragg angle,

(deg.)

Figure

4.13.

Observed and calculated intensity in

fragment of the powder diffraction pattern

of NiMn02(OH) after adding two broad peaks at

35.4

and

-40.8'.

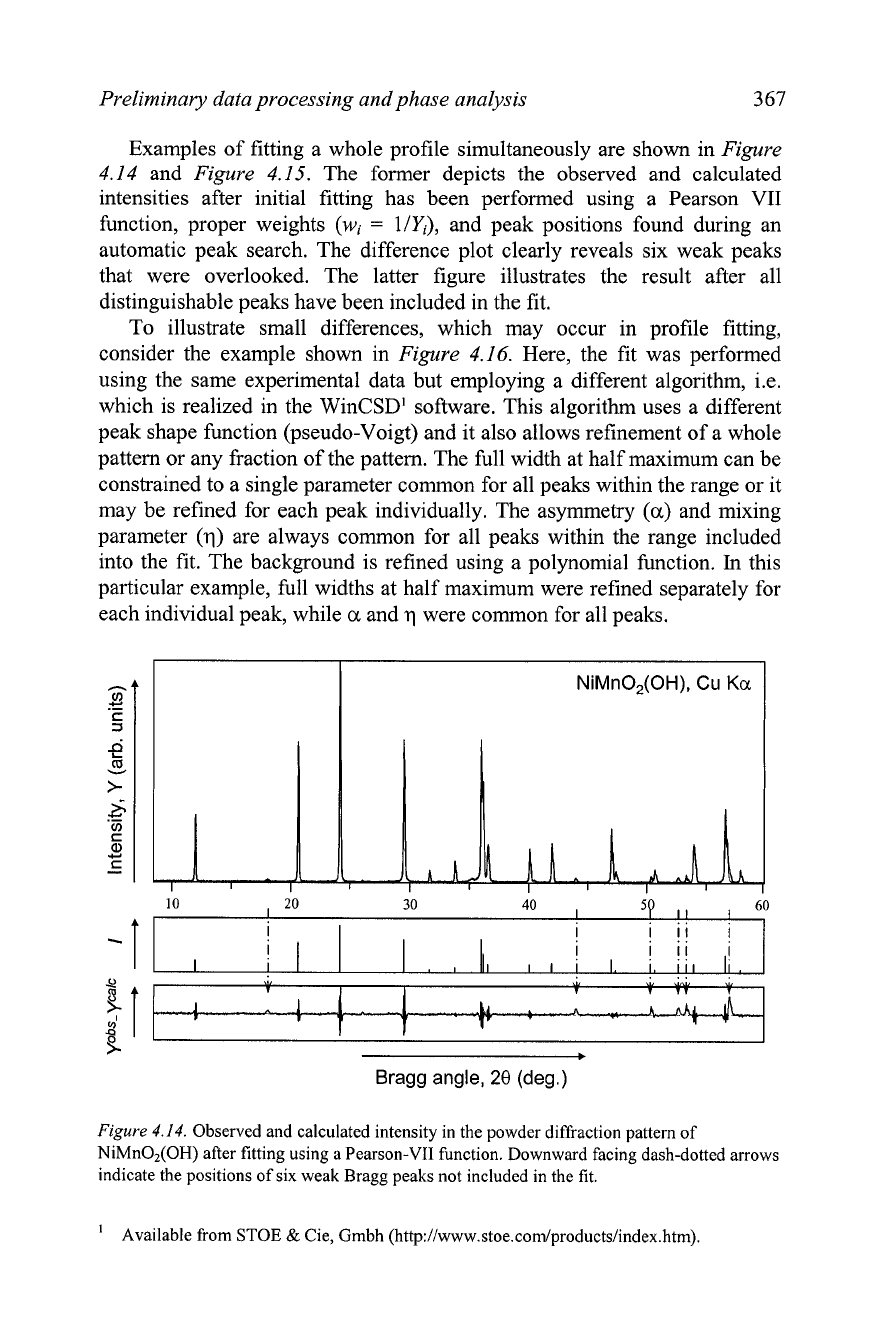
Preliminary data processing and phase analysis

367

Examples of fitting a whole profile simultaneously are shown in

Figure

4.14

and

Figure

4.15.

The former depicts the observed and calculated

intensities after initial fitting has been performed using a Pearson

VII

function, proper weights

(wi

l/Yi),

and peak positions found during an

automatic peak search. The difference plot clearly reveals six weak peaks

that were overlooked. The latter figure illustrates the result after all

distinguishable peaks have been included in the fit.

To illustrate small differences, which may occur in profile fitting,

consider the example shown in

Figure

4.16.

Here, the fit was performed

using the same experimental data but employing a different algorithm, i.e.

which is realized in the WinCSD1 software. This algorithm uses a different

peak shape function (pseudo-Voigt) and it also allows refinement of a whole

pattern or any fraction of the pattern. The full width at half maximum can be

constrained to a single parameter common for all peaks within the range or it

may be refined for each peak individually. The asymmetry

(a)

and mixing

parameter (q) are always common for all peaks within the range included

into the fit. The background is refined using a polynomial function.

this

particular example, full widths at half maximum were refined separately for

each individual peak, while

and q were common for all peaks.

Figure

4.14.

Observed and calculated intensity in the powder diffraction pattern of

NiMnO,(OH) after fitting using a Pearson-VII function. Downward facing dash-dotted arrows

indicate the positions of six weak Bragg peaks not included in the fit.

Available from STOE

Cie, Gmbh

(http:Nwww.stoe.corn/products/index.htm).

! !

1,111

. ..

Bragg angle,

(deg.)

368

Chapter

Bragg angle,

(deg.)

Figure

4.15.

Observed and calculated intensity in the powder diffraction pattern of

NiMnO,(OH) after the completion of profile fitting using the DMSNT program.

symmetrical Pearson-VII function was employed and all present Bragg peaks were included

in the fit. The box at the bottom shows the difference between the observed and calculated

intensities using the same scale as on the plot of both

PbS

and

Yale.

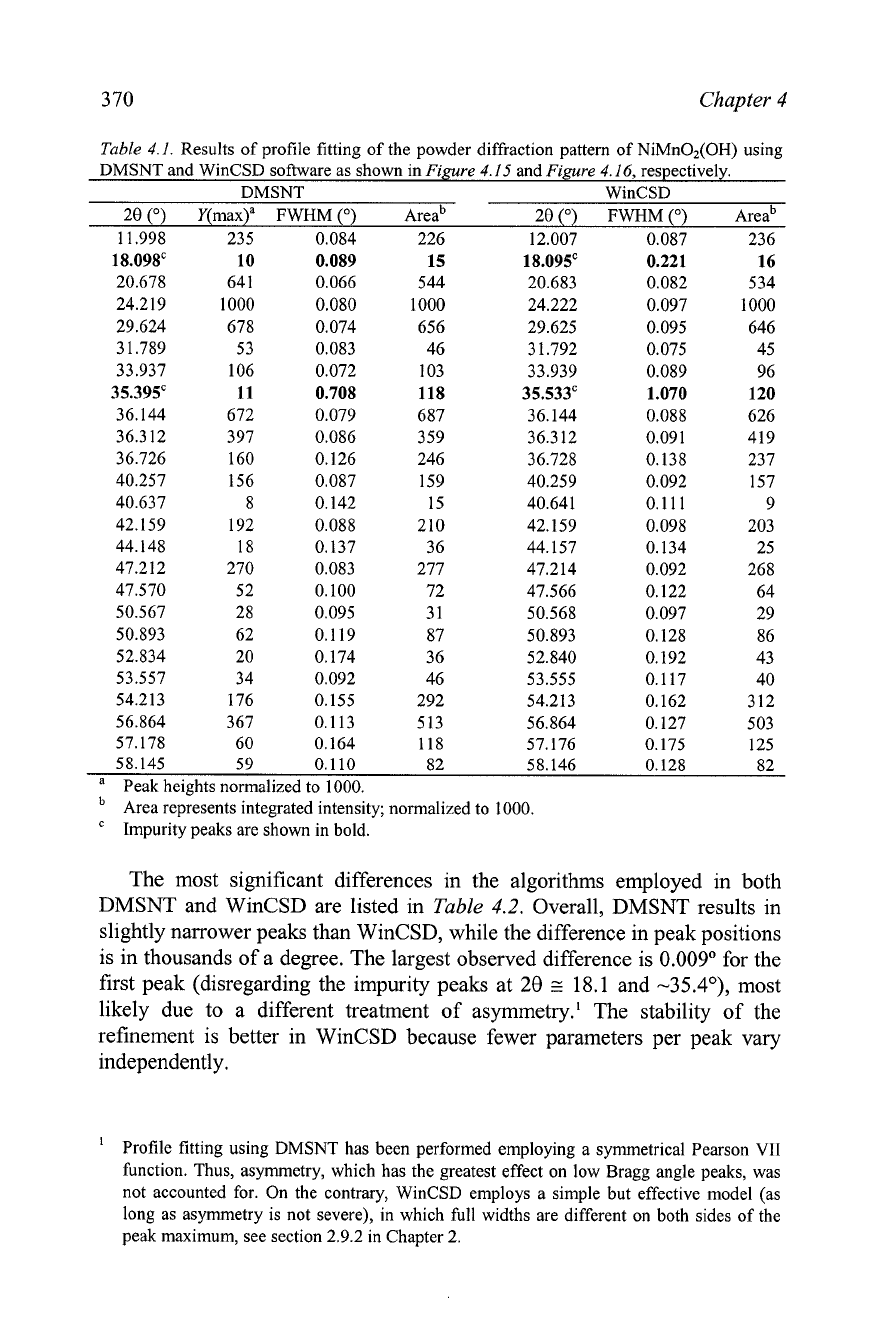
The values of the observed Bragg angles, full widths at half maximum,

and integrated intensities obtained using both the DMSNT and WinCSD

programs are assembled in

Table

4.1.

The differences in Bragg angles and

intensities of sharp peaks are statistically insignificant. The average FWHM

varies from -0.08" at the beginning to -0.14' at the end of the pattern. Thus,

the broad peak at

35.4" likely belongs to an impurity phase.' Full

widths at half maximum of several weak Bragg reflections are noticeably

inflated, which often happens when weak peaks are fitted using individual

FWHM's. As seen in

Figure

4.1

the general trend in the two distributions

of FWHM as functions of Bragg angle is normal. However, the deviations

from dependencies discussed in section

2.9.1

are substantial, especially for

weak peaks. The spread in FWHM's can be reduced by increasing quality of

the data (by improving counting statistics) andlor by improving the stability

of non-linear least squares using a choice of FWHM constraints.

Weak Bragg reflection at

18.1'

also belongs to an impurity, present in this powder

sample. Its full width at half maximum determined using DMSNT is nearly identical to

those of neighboring peaks, while

WinCSD indicates a much broader peak shape.

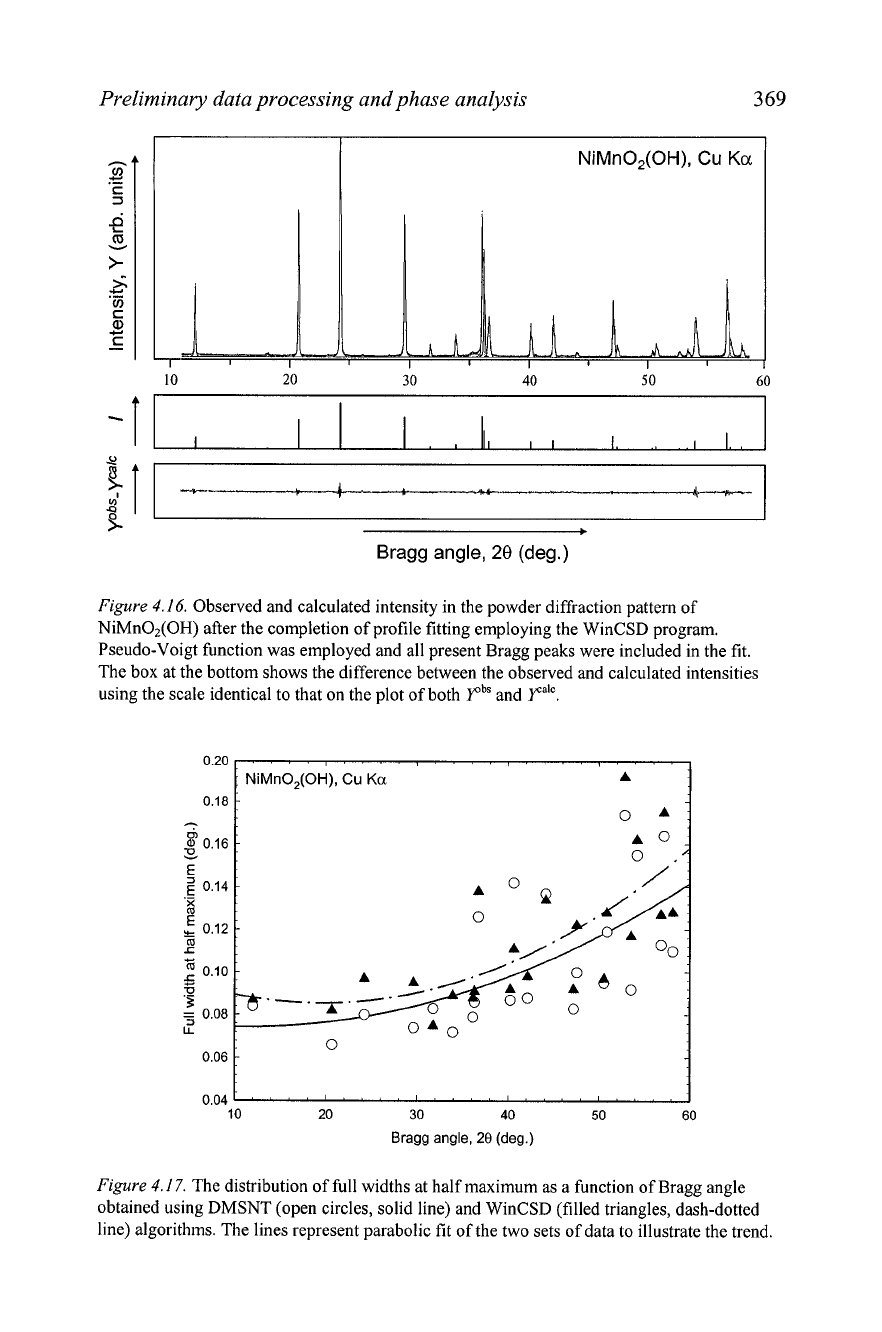
Preliminary data processing and phase analysis

Figure

4.16.

Observed and calculated intensity in the powder diffraction pattern of

NiMn02(0H) after the completion of profile fitting employing the WinCSD program.

Pseudo-Voigt function was employed and all present Bragg peaks were included in the fit.

The box at the bottom shows the difference between the observed and calculated intensities

using the scale identical to that on the plot of both

PbS

and

PalC.

Bragg angle,

(deg.)

Figure

4.17.

The distribution of full widths at half maximum as a function of Bragg angle

obtained using DMSNT (open circles, solid line) and WinCSD (filled triangles, dash-dotted

line) algorithms. The lines represent parabolic fit of the two sets of data to illustrate the trend.

-----i-

Bragg

angle,

(deg.)

Chapter

Table

Results of profile fitting of the powder diffraction pattern of NiMn02(OH) using

DMSNT and WinCSD software as shown in

Figure

4.15

and

Figure

4.16,

respectively.

DMSNT WinCSD

(O)

Y(rna~)~ FWHM

(")

Areab

(")

FWHM

(")

Areab

58.145

0.110 82 58.146 0.128 82

Peak heights normalized to 1000.

Area represents integrated intensity; normalized to 1000.

Impurity peaks are shown in bold.

The most significant differences in the algorithms employed in both

DMSNT and WinCSD are listed in

Table

4.2.

Overall, DMSNT results in

slightly narrower peaks than WinCSD, while the difference in peak positions

is in thousands of a degree. The largest observed difference is

0.009"

for the

first peak (disregarding the impurity peaks at

18.1

and -35.4"), most

likely due to a different treatment of asymmetry.' The stability of the

refinement is better in WinCSD because fewer parameters per peak vary

independently.

Profile fitting using DMSNT has been performed employing a symmetrical Pearson VII

function. Thus, asymmetry, which has the greatest effect on low Bragg angle peaks, was

not accounted for. On the contrary, WinCSD employs a simple but effective model (as

long as asymmetry is not severe), in which full widths are different on both sides of the

peak maximum, see section

2.9.2

in Chapter