Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений

Подождите немного. Документ загружается.

7.3. Итеративное сплетение 301











i,t





i,1

i,4









- -

i,1

i,2

i,3

i,4

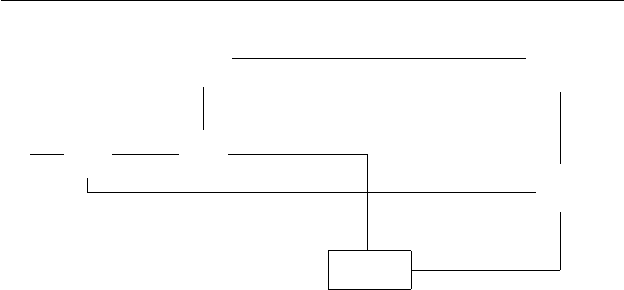
Рис. 7.3. Имитация сплетения в M

тивного сплетения в соответствии с σ, воспользуемся индукци-

ей по параметру compl(π) — сложности допустимых путей π

(т. е. последовательностей состояний) из M

Для последовательности π состояний s

, s

, . . . , s

∈ K ∪K

таких, что s

∈ F , s

j+1

∈ δ

, α

) при α

∈ V ∪ {λ}, где

0 6 j 6 p − 1, обозначим через compl(π) вектор (c

, . . . , c

) из

, где c

— число начальных или заключительных переходов

из π уровня k, т. е. число индексов l, таких, что s

l+1

∈ δ

, λ).

Введем на множестве N

обратный лексикографический по-

рядок: (c

, . . . , c

) < (d

, . . . , d

), если существует индекс j,

1 6 j 6 m, такой, что c

= d

при i > j и c

< d

. Поскольку это

отношение является полным порядком, мы можем воспользо-

ваться им для индукции.

Для того же допустимого пути π обозначим через yield(π)

распознаваемую строку α

. . . α

p−1

Если π — допустимый путь с compl(π) = (0, 0, . . . , 0), то

очевидно, что yield(π) лежит в L, а значит, и в σ

∗

(L).

Пусть (c

, . . . , c

) ∈ N

, (c

, . . . , c

) > (0, 0, . . . , 0), и дл я

всех допустимых путей π с условием compl(π) < (c

, . . . , c

)

строка yield(π) принадлежит σ

∗

(L). Рассмотрим допустимый

путь π из M

, такой, что compl(π) = (c

, . . . , c

). (Если таких

путей не существует, индуктивный шаг выполняется по умол-

302 7. Системы сплетения

чанию.) Путь π должен иметь следующий вид:

π = s

, s

, . . . , s

, s

∈ F.

Поскольку он начинается состоянием s

∈ K, заканчивается

состоянием s

∈ F ⊆ K и compl(π) > (0, . . . , 0), в нем присут-

ствуют переходы. От K к K

можно перейти лишь с помощью

начальных переходов, а от K

к K — только с помощью за-

ключительных, поэтому существуют s

, s

, 1 6 j

< j

< p,

такие, что s

= q

i,1

, s

= q

i,t

, и все s

при j

6 j 6 j

лежат в K

(проход автоматом через u

i,1

i,4

определен одно-

значно: если следующий после п опад ания в q

i,1

переход яв-

ляется заключительным, то после него мы обязательно попа-

даем в q

i,t

). Следовательно, существует правило сплетения

r = u

i,1

i,2

i,3

i,4

, в соответствии с которым и была вве-

дена указанная пара переходов.

Предположим, что переход, соответствующий s

, имеет

уровень k, а переход, соотв етствующий s

, — уровень k

. Тогда

существует допустимый путь π

= s

, . . . , s

−1

, s

, . . . , s

из

k−1

, такой, что s

∈ F и

yield(s

, . . . , s

−1

) = x

yield(s

−1

, s

, . . . , s

) = u

i,1

i,2

для некоторых x

, x

∈ V

∗

. Аналогично, существует допусти-

мый путь π

= s

, s

, . . . , s

, s

, . . . , s

из M

−1

, такой, что

yield(s

, s

, . . . , s

) = y

i,3

i,4

yield(s

, . . . , s

) = y

для некоторых y

, y

∈ V

∗

. Эта ситуация изображена на

рис. 7.4. Следовательно,

(yield(π

), yield(π

)) `

yield(π).

Исследуем теперь сложность пути π

, для π

все анало-

гично. Разложение u

i,1

i,2

(прохождение от s

−1

к s

∈ F )

осуществляется в M

k−1

, следовательно, все переходы здесь —

уровня меньше k. Все переходы при прохождении от s

−1

— общие для π и π

. Итак, для compl(π

) = (d

, . . . , d

)

7.3. Итеративное сплетение 303















- -

















= q

i,t

i,1

i,4

= q

i,1

−1

i,1

i,2

i,3

i,4

Рис. 7.4. Вычисление сплетения в M

имеем d

6 c

при всех j > k. Кроме того, путь π содержит

по меньшей мере один не содержащийся в π

переход уровня

k: от s

−1

к s

. Это означает, что d

< c

. Следователь-

но, (d

, . . . , d

) < (c

, . . . , c

), что завершает индуктивное

рассуждение, а значит, и все доказательство.

Более сильный результат приведен в [270]; найти его по-

дробное доказательство можно также в [139].

Лемма 7 .15. Если семейство FL является полным AFL, то

(F L, F IN) ⊆ F L.

На самом деле, в [139] доказан еще более сильный резуль-

тат, поскольку утверждение леммы 7.15 остается справедли-

вым для любого содержащего регулярные языки семейства F L,

замкнутого относительно левых и правых частных при деле-

нии на регулярные языки и относительно подстан овок внутри

регулярных языков. (Если s : V

∗

−→ P(U

∗

) — подстановка,

такая, что s(a) ∈ F L для всех a ∈ V и L ⊆ V

∗

— регуляр-

ный язык, то s(L) ∈ F L. Каждое полное AFL обладает этим

свойством, см. теорему 11.5 из [145].)

304 7. Системы сплетения

Лемма 7.16 (основная лемма об универсальности). Любой

язык L ∈ RE, L ⊆ T

∗

, может быть представлен в виде

L = L

∩ T

∗

для некоторого L

∈ H

(F IN, REG).

Доказательство. Рассмотрим порождающую L грамматику

типа 0 G = (N, T, S, P ), обозначим U = N ∪ T ∪ {B}, где B —

новый символ, и построим H-схему

σ = (V, R ),

где

V = N ∪ T ∪ {X, X

, B, Y, Z} ∪ {Y

| α ∈ U},

а R содержит следующие группы правил:

Имитация : 1. Xw#uY $Z#vY при u → v ∈ P, w ∈ U

∗

Переброска : 2. Xw#αY $Z#Y

при α ∈ U, w ∈ U

∗

3. X

α#Z$X#wY

при α ∈ U, w ∈ U

∗

4. X

w#Y

$Z#Y при α ∈ U, w ∈ U

∗

5. X#Z$X

#wY при w ∈ U

∗

Завершение : 6. #ZY $XB#wY при w ∈ T

∗

7. #Y $XZ#.

Рассмотрим также язык

= {XBSY, ZY, XZ}

∪ {ZvY | u → v ∈ P } ∪ {ZY

, X

αZ | α ∈ U}.

Утверждается, что L = σ

∗

) ∩ T

∗

Действительно, исследуем работу σ, точнее, возможности

получать строки из T

∗

Ни одна строка из L

не лежит в T

∗

. Все правила из R вклю-

чают строки, содержащие символ Z, в то же время он не может

появиться в строке, пол ученно й путем сплетения. Поэтому на

каждом шаге мы должны задействовать строку из L

и стро-

ку, полученную на предыдущем шаге, за исключением XBSY

из L

Символ B отмечает начало сентенциальных форм грамма-

тики G, моделируемых σ.

7.3. Итеративное сплетение 305

С помощью правил из группы 1 мы можем имитировать

выполнение правил из P . Пра вила из групп 2–5 перебрасыва-

ют символы c правого конца текущей строки на левый конец,

делая возможным имитацию правил из P на правом конце по-

лучаемой строки. Понять же, какова эта строка в действитель-

ности, мы всегда сможем благодаря п остоянному присутствию

символа B, помечающего начала сентенциальных форм грам-

матики G. Другими словами, если текущая строка в σ имеет

вид β

при некоторых β

, β

из X, X

, Y, Y

(α ∈ U), и

, w

∈ (N ∪ T )

∗

, то w

— сентенциальная форма в G.

Мы начинаем с XBSY , т. е. с аксиомы грамматики G, по-

меченной с левой стороны символом B и заключенной между

маркерами X, Y .

Посмотрим, как работают правила 2–5. Возьмем строку

XwαY при некоторых α ∈ U, w ∈ U

∗

. По правилу типа 2 мы

получаем

(Xw|αY, Z|Y

) ` XwY

Символ Y

запоминает, что с правого конца строки wα сти-

рается буква α. К XwY

не может быть применено ни одно

правило из R, кроме правил типа 3:

α|Z, X|wY

) ` X

αwY

Заметим, что тот же символ α, который был удален на преды-

дущем шаге, теперь добавлен перед w. Продолжить можно

опять лишь одним способом, исп ользо вав правило типа 4. По-

лучим

αw|Y

, Z|Y ) ` X

αwY.

Применение правила типа 7, стир ающего Y , не позволит нам

затем удалить X

(и B) и превратить строку в терминальную.

Поэтому мы должны использовать правило типа 5:

(X|Z, X

|αwY ) ` XαwY.

Начав с XwαY , мы получили XαwY , строку с теми же марке-

рами. Мы можем сколько угодно повторять эти шаги, произ-

водя таким образом любые циклические перестановки строк,

заключенных между X и Y . Более того, ничего кроме цикли-

306 7. Системы сплетения

ческих перестановок получить мы не сможем (в частности, на

каждом шаге в строку будет входить ровно один символ B).

Правило типа 1 также можно применить к каждой строке

XwY , у которой w оканчивается левой частью правила из P .

Подготовив же строку с помощью правил из групп 2–5, как

описывалось выше, мы сможем имитировать выполнение лю-

бого правила из P в любом месте соответствующей сентенци-

альной формы грамматики G.

Следовательно, для каждой сентенциальной формы w из G

существует строка XBwY , полученная с помощью σ, и обрат-

но, в строке Xw

Y , построенной σ, w

есть сентенциаль-

ная форма грамматики G.

Удалить символы, не лежащие в T , из построенных с по-

мощью σ строк можно только, воспользовавшись правилами

групп 6, 7. Более точно, символы XB могут быть удалены т оль-

ко при следующих условиях:

(1) в наличии имеется Y (т. е. ра бота будет заблокирована, если

воспользоваться сначала правилом 7, стирающим Y : строка

не сможет участвовать в дальнейших сплетениях, а терми-

нальной она не является),

(2) текущая строка, ограниченная X, Y , состоит только из тер-

минальных символов и одного символа B,

(3) символ B расположен слева.

После удаления X и B можно стереть и Y , а то, что мы полу-

чим, будет строкой из T

∗

. Из предыдущего обсуждения ясно,

что она лежит в L(G), значит, σ

∗

) ∩ T

∗

⊆ L(G). Обратно,

каждая строка из L(G) может быть построена таким спосо-

бом, следовательно, L(G) ⊆ σ

∗

)∩T

∗

. Получаемое равенство

L(G) = σ

∗

) ∩ T

∗

завершает доказательство.

В следующих главах встретится много вариантов процеду-

ры переброски и имитации, использованной в данном доказа-

тельстве.

Семейства H

(F L

, F L

) удовлетворяют сильным ограни-

чениям.

7.3. Итеративное сплетение 307

Лемма 7.17. Пусть FL — семейство языков, замк нутое от-

носительно пересечения с регулярными языками и ограничен-

ных морфизмов. Тогда для каждого L ⊆ V

∗

, L /∈ F L, и c, d /∈ V ,

имеем L

/∈ H

(F L, RE) при

= (dc)

∗

L(dc)

∗

∪ c(dc)

∗

L(dc)

∗

Доказательство. Для L, c, d из условия леммы обозначим

= (dc)

∗

L(dc)

∗

= c(dc)

∗

L(dc)

∗

Из L = L

∩ V

∗

= L

∩ V

∗

и L = h(L

∩ cV

∗

d), где h —

морфизм, определяемый соотношениями h(a) = a, a ∈ V и

h(c) = h(d) = λ, следует L

/∈ F L, L

/∈ F L и L

= L

∪L

/∈ F L.

Предположим, что L

= σ

∗

) для некоторого L

∈ F L,

⊆ L

и σ = (V, R) с произвольным R. Из L

/∈ F L следует

6= L

. Поэтому, чтобы пол учить L

, мы должны провести хо-

тя бы одно сплетение (x, y) `

z, x, y ∈ L

. Пусть x = x

y = y

для некоторых x

, x

, y

∈ (V ∪ {c, d})

∗

и r =

∈ R. Тогда, если x ∈ L

, то x

= cxd ∈ L

= cx

d. Следовательно, можно выполнить сплетение

, y) `

= cx

= cz. Если z ∈ L

, то cz /∈ L

, противо-

речие.

Следовательно, строка x дол жн а быть взята из L

. Тогда

= dxc ∈ L

, x

= dx

c, и значит, можно выполнить

сплетение (x

, y) `

= d x

= d z. Мы снова получаем

строку, не лежащую в L

Поскольку любое сплетение провоцирует появление не ле-

жащих в L

строк, мы должны заключить, что σ

∗

) = L

Это противоречит условию L

6= L

Так как тип множества R не играет никакой роли в преды-

дущих рассуждениях, имеем L

/∈ H

(F L, RE).

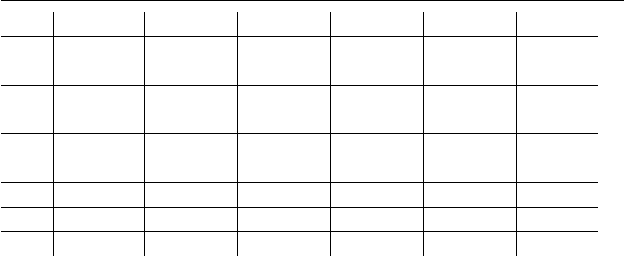
Теорема 7.3. Имеют место соотношения, приведенные

в таблице 7.2, где на пересечении строки, отмеченной

F L

, и столбца, отмеченного F L

, стоит либо семейство

(F L

, F L

), либо пара семейств FL

, F L

, таких, что

308 7. Системы сплетения

F IN REG LIN CF CS RE

F IN F IN, FIN, F IN, F IN, F IN, F IN,

F IN REG RE RE RE RE RE

REG REG REG, REG, REG, REG, REG,

REG REG RE RE RE RE RE

LIN LIN, LIN, LIN, LIN LIN, LIN,

LIN CF RE RE RE RE RE

CF CF CF, RE CF, RE CF, RE CF, RE CF, RE

CS CS, RE CS, RE CS, RE CS, RE CS, RE CS, RE

RE RE RE R E RE RE RE

Таблица 7.2. Размеры семейств H

(F L

, FL

F L

⊂ H

(F L

, F L

) ⊂ F L

. Семейства F L

, F L

являются

наилучшими возможными гра ницами среди рассматриваемых

здесь ш ести семейств.

Доказательство. В силу леммы 7.12 F L

⊆ H

(F L

, F L

)

при любых F L

, F L

. С другой стороны, H

(F L

, F L

) ⊆ RE

для всех F L

, F L

. За исключением семейств H

(RE, F L

совпадающих с RE, все включения H

(F L

, F L

) ⊆ RE соб-

ственные, так как по лемме 7.17 непусты следующие разности:

REG−H

(F IN, RE), LIN −H

(REG, RE), CF −H

(LIN, RE),

CS − H

(CF, RE), RE − H

(CS, RE).

Из лемм 7.14 и 7.12 следует, что H

(REG, F IN) = REG.

Значит, H

(F IN, F IN) ⊆ REG. Это включение собственное

по лемме 7.17.

Из леммы 7.13 и результатов раздела 7.2 получаем стро-

гость включен ий LIN ⊂ H

(LIN, F IN) и CS ⊂ H

(CS, F IN).

Тот же результат получается при замене F IN на произвольное

семейство F L

Из лемм 7.1 5 и 7.12 вытекает равенство H

(CF, F IN) = CF.

Кроме того, H

(LIN, F IN) ⊆ CF . Это включение собственное

по лемме 7.17.

Из той же леммы следует, что RE является наилучшим

приближением для H

(F L

, F L

), F L

6= F IN (действитель-

но, H

(F IN, REG) − F L 6= ∅ для всех семейств F L ⊂ RE, за-

мкнутых относительно пересечения с регулярными языками).

7.3. Итеративное сплетение 309

Остается доказать утверждение о том, что H

(F IN, F IN)

содержит бесконечные языки. Это так даже для H

(F IN, [1]):

при σ = ({a}, {a#$#a}) имеем σ

∗

({a}) = a

. Таким о бразом,

доказательство теоремы завершено.

Из соотношений таблицы 7.2 можно сделать ряд интерес-

ных выводов:

1. Итеративное сплетение р егулярных (и даже конечных) язы-

ков относител ьно регулярного множества правил дает нере-

гулярные (и даже нерекурсивные) языки (это не так в слу-

чае более «слабого» неитеративного сплетения). Поэтому

результат леммы 7.14 не может быть улучшен.

2. Итеративное сплет ение конечных языков относительно (по

меньшей мере) регулярного множества правил дает язы-

ки, не являющиеся контекстными. Фактически для всех се-

мейств F L

, содержащих регулярные языки, пересечения

языков из H

(F L

, F L

) с регулярными языками вида V

∗

характеризуют семейство рек урсивн о перечислимых язы-

ков.

3. С другой стороны, для всех семейств H

(F L

, F L

), та-

ких, что F L

6= RE, выполняются довольно неожиданные

ограничения. Если F L

— наименьшее из рассматриваемых

здесь семейств, строго содержащее F L

, то при всех F L

включая F L

= R E, имеются языки из F L

, не лежащие в

(F L

, F L

Ввиду равенств H

(F L, F IN) = F L для F L ∈ {REG, CF,

RE} иерархии, основ анные на радиусе H-схем, в этих случаях

схлопываются. Аналогичная проблема для F L ∈ {LIN, CS}

все еще открыта. В случае же F IN имеется

Теорема 7.4. Выполняются строгие включения

F IN ⊂ H

(F IN, [1]) ⊂ H

(F IN, [2]) ⊂ . . .

⊂ H

(F IN, F IN) ⊂ REG.

Доказательство. Включения следуют из определений и

лемм 7.12 и 7.14. Строгость первого и последнего включений

уже известна.

310 7. Системы сплетения

Для k > 1 рассмот рим язык

= {a

| n > 2k + 1}.

Он принадлежит H

(F IN, [k + 1]), поскольку L

= σ

∗

) при

= {a

2k+2

σ = ({a, b}, {a

k+1

}).

Действительно, правило сплетения может быть применено

только к подстрокам u

= a

2k+1

и u

= a

2k+1

центральных

подстрок a

2k+i

(i > 1) строк из L

. Следовательно, для любого

i > 0 мы можем получить строку с цен трал ьной подстрокой

2k+i+1

с помощью сплетений вида

k+1

, a

k+1

)

` a

k+1

, a

k+1

)

` a

k+1

при j > 1.

Предположим, что L

= σ

∗

) для некоторого конечного

языка L

и H-схемы σ

= (V, R) с условием rad(σ

) 6 k. Возь-

мем правило r = u

∈ R и две строки x, y ∈ L

, к ко-

торым это правило может быть применено, x = a

n > 2k+1, y = y

. По условию |u

| 6 2k . Поэтому, если

∈ a

∗

, то u

является подстрокой и префикса a

, и суф-

фикса a

, и центрального подслова a

в x. Аналогично, если

∈ b

∗

, то u

— подстрока обеих подстрок b

в x. Е сли

∈ a

, то u

является подстрокой и префикса a

, и

подслова a

из x; если u

∈ b

, то u

— подстрока и

суффикса b

, и подслова b

в x. В любом случае, спле-

тение x, y по правилу r приводит к появлению по крайней мере

одной строки, не лежащей в L

. Значит, равенство L

= σ

∗

)

невозможно. Поэтому H

(F IN, [k + 1]) − H

(F IN, [k]) 6= ∅ при

всех k > 1.