Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений

Подождите немного. Документ загружается.

Глава 7

Системы сплетения

Начиная с этой главы, мы будем исследовать модели вычис-

лимости, основанные на операции сплетения, которая на фор-

мальном уровне имитирует рекомбинантное поведение молекул

ДНК, проявляющееся под влиянием рестриктаз и лигаз. Говоря

неформально, процесс сплетения двух строк включает в себя

их рассечение в местах, задаваемых данными подстроками (они

соответствуют сайтам узнавания для рестриктаз), и перекрест-

ное сц еплен ие полученных фрагментов (что отвечает реакции

сшивки).

После краткого обсуждения пер ехода от операции реком-

бинации, происходящей in vivo, к абстрактной операции спле-

тения, мы начинаем математическое изучение последней, ис-

следуя как итеративный, так и неитеративный случаи. Далее

мы определяем фундаментальное понятие следующих глав —

понятие расширенной H-системы, порождающего устройства,

использующего в качестве основной составляющей операцию

сплетения. В данной главе мы обсудим операцию сплетения и

системы сплетения в общей и простой фор мах. Как выяснится,

H-системы с конечными компонентами могут порождать лишь

регулярные языки, поэтому в следующих главах мы рассмот-

рим дополнительные управляющие механизмы, р егулирующие

работу H-систем. Мы исследуем механизмы, подсказанные как

теорией регулируемых переписывающих систем (в главе 8), так

и теорией грамматических систем (в главе 10). В большинстве

случаев мы получим характеризации рекурсивно перечисли-

мых языков, а значит, вычислительную полноты. Из соответ-

ствующих доказательств при этом извлекаются универсальные

H-системы рассматриваемых типов.

282 7. Системы сплетения

7.1 От рекомбинации ДНК к операции сплетения

Давайте начнем с примера, иллюстрирующего разрезание и

склеивание, осуществляемые in vitro рестриктазами и лигаза-

ми на двойных цепочках, и сходного с рекомбинацией ДНК,

происходящей in vivo.

Рассмотрим следующие три молекулы ДНК:

− ЦЦЦЦЦТЦГАЦЦЦЦЦ − 3

− ГГГГГАГЦТГГГГГ − 5

− АААААГЦГЦААААА − 3

− ТТТТТЦГЦГТТТТТ − 5

− ТТТТТГЦГЦТТТТТ − 3

− АААААЦГЦГААААА − 5

Рестрикционные ферменты (эндонуклеазы) умеют распо-

знавать определенные подстроки двойных цепочек ДНК и раз-

резать последние, создавая либо «прямые», либо «липкие» кон-

цы. Например, последовательности, разрезаемые ферментами

TaqI, SciNI и HhaI, суть соответственно:

Ц Г Ц Г Ц Г Ц Г

ЦГЦГЦГЦГАГЦТ

А Г Ц Т

Мы уже обсуждали этот способ разрезания молекул ДНК.

В частности, воздействуя на три приведенные выше молекулы,

ферменты TaqI, SciNI и HhaI однозначно выберут места для

рассечений, в результате чего возникнут шесть фрагментов:

− ЦЦЦЦЦТ ЦГАЦЦЦЦЦ − 3

− ГГГГГАГЦ ТГГГГГ − 5

− АААААГ ЦГЦААААА − 3

− ТТТТТЦГЦ ГТТТТТ − 5

− ТТТТТГЦГ ЦТТТТТ − 3

− АААААЦ ГЦГААААА − 5

7.1. От рекомбинации ДНК к сплетению 283

Заметим, что во всех случаях мы получаем фрагменты с

одинаковым, если читать в направлении от 5

к 3

, выступом

ЦГ, но есть важное различие между случаем TaqI, SciNI и слу-

чаем HhaI: у выст упов, создаваемых первыми двумя фермен-

тами, свободны 5

-концы, в то время как у обоих выступов,

создаваемых HhaI, свободны 3

-концы. Концы первых четы-

рех фрагментов совместимы. В результате сшивки они могут

соединиться вместе, либо восстанавливая исходные молекулы,

либо путем рекомбинации создавая новые. Рекомбинация ука-

занных четырех фрагментов приводит к возникновению следу-

ющих новых молекул:

− ЦЦЦЦЦТЦГЦААААА − 3

− ГГГГГАГЦГТТТТТ − 5

− АААААГЦГАЦЦЦЦЦ − 3

− ТТТТТЦГЦТГГГГГ − 5

Их появление возможно, поскольку выступы соответствуют

друг другу.

Таким образом, операция, которую мы должны смоделиро-

вать, состоит из двух этапов: (1) рассечение последовательно-

стей в четко определенных местах и (2) склейка фрагментов с

подходящими концами.

Благодаря комплементарности Уотсона-Крика, можно рас-

сматривать эту операцию как действие над одинарными цепоч-

ками (т. е. над строками). Для молекул ДНК этот абстрактный

шаг очевиден; например, три молекулы, с которых мы начина-

ли, соответственно отождествляются со строками

ЦЦЦЦЦТЦГАЦЦЦЦЦ,

АААААГЦГЦААААА,

ТТТТТГЦГЦТТТТТ,

при условии, что последние представляют цепочки молекул

ДНК, читаемые в направлении от 5

к 3

Для схем рестрикционных ферментов мы должны сохра-

нить не только информацию о включенных в них нуклеотидах,

но еще и о типе концов, возникающих при разрезании молекул.

Такая схема описывается тройкой строк (u, x, v) над алфави-

284 7. Системы сплетения

том {А, Ц, Г, Т}, где (u, v) — окружение, в котором происходит

рассечение, а x — выступающая последовательность. Для фер-

ментов из нашего примера это тройки

(Т, ЦГ, А), (Г, ЦГ, Ц), (Г, ЦГ, Ц).

Известно, однако, что концы, создаваемые первым и вторым

ферментами, совместимы друг с другом и не совместимы с ре-

зультатом деятельности третьего фермента, несмотря на то,

что соответствующая ему тройка ничем не отличается от трой-

ки второго фермента. Эту коллизию мы разрешим, разделив

схемы на два класса. Скажем, что первые две т ройк и лежат,

например, в Классе 1, а последняя — в Классе 2. Тогда при ре-

комбинации строк мы допустим сцепление лишь тех фрагмен-

тов, которые произведены в соответствии с тройками одного и

того же класса.

Формально, для двух строк w

, w

и троек (u

, x

, v

, x

, v

), таких что

= w

операция рекомбинации разрешена, только когда (u

, x

, v

) и

, x

, v

) — схемы одного и того же класса и x

= x

. Строки,

получающиеся в результате рекомбинации, таковы:

= w

где x = x

= x

Фактически мы сделали здесь еще одно небольшое обобще-

ние, перейдя к некоему произвольному алфавиту.

Для того чтобы получить наиболее общую операцию над

строками, моделирующую операцию, описанную выше, нужно

сделать еще три шага.

Во-первых, вместо отношения «быть из одного и того же

класса», введенного на схемах (u, x, v), мы можем рассмотреть

произвольное отношение, задаваемое непосредственно парами

((u

, x, v

), (u

, x, v

)), такими, что тройки (u

, x, v

), (u

, x, v

)

7.1. От рекомбинации ДНК к сплетению 285

из пары лежат в одном классе и дают совместимые концы, т. е.,

другими словами, фрагментам, возникающим с их помощью,

разрешено рекомбинировать.

Во-вторых, результатом рекомбинации для пар ы ((u

, x, v

)) и строк w

, w

, таких что w

= w

и w

, можно считать только строку z

= w

, по-

скольку строка z

= w

— это результат аналогичной

рекомбинации относительно симметричной пары ((u

, x, v

)).

В-третьих, вместо пар троек ((u

, x, v

), (u

, x, v

)) мы мо-

жем рассматривать пары двоек: переход от w

= w

к z

= w

в соответствии с ((u

, x, v

)) равносилен переходу от w

= w

, w

к z

= w

в соответствии с ((u

, v

), (u

, v

)),

где u

= u

x и u

= u

x. Аналогично, можно рассмотреть

четверку ((u

, xv

), (u

, xv

)).

Все это вместе подводит нас к следующей операции со стро-

ками над алфавитом V : четверка строк над V (u

, u

; u

, u

)

называется правилом сплетения; в соответствии с таким пра-

вилом r для x, y, z ∈ V

∗

мы записываем

(x, y) `

тогда и только тогда, когда

x = x

, y = y

, z = x

для некоторых x

, x

, y

∈ V

∗

. Скажем, что мы сплетаем

x, y в сайтах u

, u

соответственно и результатом явля-

ется z. Это — основная операция, с которой мы будем иметь

дело в данной главе. В следующих главах при построении мо-

делей вычислений мы будем рассматривать данную операцию

в несколько иной, более приближенной к реальности форме:

(x, y) |=

(z, w)

тогда и только тогда, когда

x = x

, y = y

z = x

, w = y

286 7. Системы сплетения

для некоторых x

, x

, y

∈ V

∗

, где r = (u

, u

; u

, u

) —

правило сплетения. Будем говорить, что ` есть операция 1-

сплетения, а |= есть 2-сплетение. Будет появляться и просто

термин «сплетение», но при этом из контекста всегда будет яс-

но, о каком типе операции идет речь. В данной главе мы имеем

дело только с 1-сплетением.

Безусловно, если мы захотим вернуть наши модели в ла-

бораторию, мы должны будем отказаться от всех вышеизло-

женных абстракций и возвратиться к рассмотрению конкрет-

ных ферментов с конкретными сайтами узнавания. Для ряда

моделей мы обсудим некоторые из возникающих при этом про-

блем. В общем случае, выразительная сила наших моделей су-

щественным образом зависит от механизмов регуляции, встро-

енных в операцию сплетения, о чем уже упоминалось в начале

данной главы. При сегодняшней лабораторной технике все эти

механизмы выглядят нереалистичными. Поэтому «компьюте-

ры», которые мы будем обсуждать, требуют для своей реализа-

ции значительных продвижений в биохимических технологиях.

Анализ возможной скорости таких пр одвижений выходит да-

леко за рамки настоящей книги.

7.2 Неитеративное сплетение как операция

над языками

В реальных обстоятельствах множество строк и множество

правил сплетения, точнее ферментов, скрывающихся за ни-

ми, конечно. Поскольку строки могут иметь произвольную

длину (здесь нет никаких априорных ограничений), вполне

естественно рассматривать языки произвольной мощности.

Не так обстоят дела с правилами спл етения: лишь немно-

гие рестрикционные ферменты производят выступы длины,

большей чем шесть. Это означает, что в схеме узнавания

(u, x, v) в большинстве случаев |x| 6 6, т. е. при рассмотре-

нии правил сплетения (u

, u

; u

, u

), длина каждой из строк

, u

весьма ограничена. В математической постановке

подобное ограничение не является необходимым. Более того,

как мы увидим в разделе 7.3, конечный набор правил даже

7.2. Неитеративное сплетение 287

при итеративном сплетении всегда сохраняет регулярность. С

вычислительной точки зрения это означает, что на этом пути

можно достичь самое большее выразительной силы конечного

автомата или регулярных грамматик Хомского. Эти наблю-

дения подталкивают к рассмотрению «произвольно длинных»

правил сплетения, т. е. бесконечных множеств правил спле-

тения. Дл я сохранения контроля над такими бесконечными

множествами мы можем представлять правила в виде строк.

Тогда их множества являются языками, и мы можем со-

относить тип этих языков с определенной классификацией,

например, с иерархией Хомского. Именно такой подход принят

в данном разделе.

Рассмотрим алфавит V и два спец иал ьных символа #, $, не

лежащие в V . Правило сплетения (над V ) — это строка вида

r = u

где u

, u

∈ V

∗

. (Для максимальной общности мы не на-

кладываем никаких огранич ений на строки u

, u

. Слу-

чаи, когда u

= λ или u

= λ, могут быть исключены как

нереальные.)

Для правила сплетения r = u

и строк x, y, z ∈

∗

мы записываем

(x, y) `

тогда и только тогда, когда

x = x

, y = y

, z = x

для некоторых x

, x

, y

∈ V

∗

(Следовательно, правило u

соответствует пра-

вилу (u

, u

; u

, u

) из конца предыдущего раздела.)

Строки x, y иногда н азывают термами сплетения; часто мы

будем опускать индекс r и писать ` вместо `

, если смысл будет

понятен из контекста.

Переход от x, y к z с помощью `

может быть представлен,

как показано на рис. 7.1.

Часто при сплетении конкретных строк мы будем для

наглядности отмечать вертикальной чертой место, где термы

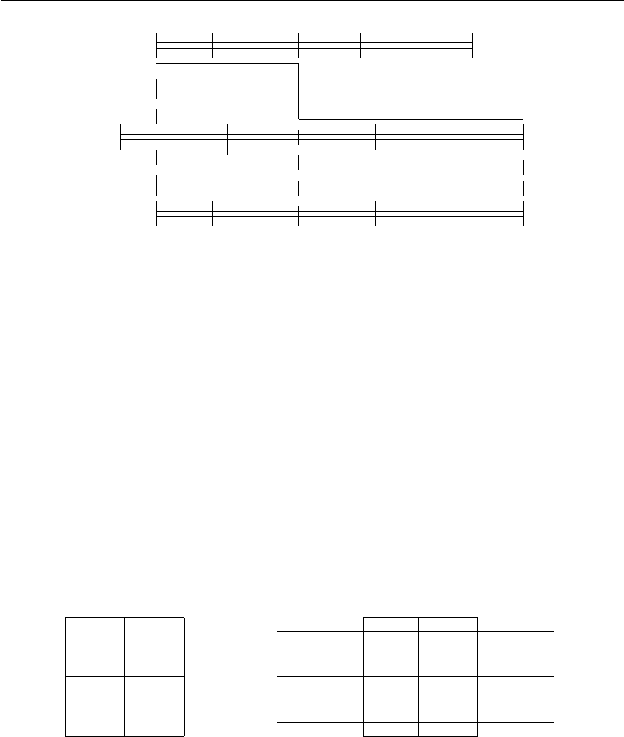
288 7. Системы сплетения

? -

Рис. 7.1. Операция сплетения.

сплетения разрезаются, например:

, y

) `

для r = u

При такой записи становится наглядным и сам способ

построения результата: к префиксу первого терма сплетения

приписывается суффикс втор ого. Она также может быть по-

лезна при графическом представлении правил сплетения, как

на рис. 7.2(a). Поясним способ работы этих правил: «окно» на

рис. 7.2(а) должно одновременно совпасть с сай тами u

в двух молекулах ДНК, как на рис. 7.2(б).

а) б)

. . .

Рис. 7.2. Графическое представление правила сплетения.

Пару

σ = (V, R ),

где V — алфавит, а R ⊆ V

∗

— множество п рави л

сплетения, будем называть H-схемой.

Заметим, что язык R может быть бесконечным, и можно

рассмотреть его место в иерархии Хомского или в другой клас-

7.2. Неитеративное сплетение 289

сификации языков. Вообще, если R ∈ F L для данного семей-

ства языков F L, то мы будем говорить, что H-схема σ имеет

тип F L.

Для H-схемы σ = (V, R) и языка L ⊆ V

∗

положим

(L) = {z ∈ V

∗

| (x, y) `

z для некоторых x, y ∈ L, r ∈ R}.

Другими словами, σ

(L) есть результат однократного 1-

сплетения строк из L в соответствии с правилами из R.

Иногда для данной H-схемы σ = (V, R) и упорядоченной

пары (x, y), x, y ∈ V

∗

, мы также обозначаем

(x, y) = {z ∈ V

∗

| (x, y) `

z для некоторых r ∈ R}.

Заметим, что σ

(x, y) отличается от множества σ

({x, y}).

Последнее есть объединение четырех множеств σ

(x, x),

(x, y), σ

(y, x), σ

(y, y). Мы можем запи сать

(L) =

[

x,y∈L

(x, y).

Для двух семейств языков F L

, F L

мы обозначаем

(F L

, F L

) = {σ

(L) | L ∈ F L

и σ = (V, R) пр и R ∈ F L

(Индекс 1 в S

(. . . , . . . ) напоминает нам, что мы пользуемся

операцией 1-сплетения.)

Семейство F L

замкнуто относительно сплетения типа F L

(или, короче, «F L

сплетения»), если S

(F L

, F L

) ⊆ F L

. Во-

обще, возможности F L

сплетения оцени ваются при исследо-

вании для разных F L

семейств S

(F L

, F L

Мы будем рассматривать семейства S

(F L

, F L

) для F L

F L

из множества {F IN, REG, LIN, CF, CS, RE} (следо ва-

тельно, всегда будет предполагаться, что F L

содержит по

меньшей мере все конечные языки). Сначала мы установим

справедливость серии лемм, связывающих операц ию сплете-

ния с другими операциями над языками, затем соберем эти

результаты о семействах S

(F L

, F L

) в одну теорему.

Лемма 7.1. Дл я любых семейств F L

, F L

из

включений F L

⊆ F L

и F L

⊆ F L

следует S

(F L

, F L

) ⊆

(F L

, F L

290 7. Системы сплетения

Доказательство. Очевидно в силу определений.

Лемма 7.2. Пусть F L

— семейство языков, замкнутое

относительно приписывания символов. Тогда при любом F L

F L

⊆ S

(F L

, F L

Доказательство. Возьмем L ⊆ V

∗

, L ∈ F L

и c /∈ V . Тогда

= L{c} ∈ F L

. Для H-схемы σ = (V ∪ {c}, {#c$c#}) имеем

L = σ

), откуда L ∈ S

(F L

, F L

) при любом F L

Лемма 7.3. Пусть FL — семейство языков, замкнутое отно-

сительно произведения и произвольных ОПМ-отображений.

Тогда FL замкнуто относительно REG сплетения.

Доказательство. Возьмем L ⊆ V

∗

, L ∈ F L и H-схему σ =

(V, R) при R ⊆ V

∗

, R ∈ REG. Рассмотрим новый

символ c /∈ V и конечный автомат M = (K, V ∪ {#, $}, s

, F, δ),

распознающий язык R. С помощью стандартного построения

мы можем получ ить ОПМ g, ассоциированную с M, которая

преобразует каждую строку вида

w = x

при x

, x

, y

∈ V

∗

, u

∈ R в строк у

g(w) = x

Следовательно, σ

(L) = g(L{c}L). Из свойств замкнутости F L

получаем σ

(L) ∈ F L.

Лемма 7.4. Пусть FL — семейство языков, замкнутое от-

носительно объединения, приписывания символов и FIN спле-

тения. Тогда FL замкнуто относительно произведения.

Доказательство. Возьмем два произвольных языка L

, L

из

F L, L

, L

⊆ V

∗

, и рассмотрим H-схему

σ = (V ∪ {c

, c

}, {#c

#}),

в которой c

, c

/∈ V — дв а новых символа. Очевидно, что

= σ

} ∪ {c

), откуда L

∈ F L.

Лемма 7.5. Пусть FL — семейство языков, замкнутое от-

носительно приписывания символов и FIN сплетения. Тогда

FL замкнуто относительно операций Pref и Suf.