Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений
Подождите немного. Документ загружается.


5.3. Характеризации RE языков 211
мый язык является проекцией некоторого языка L
u
(M), где
M — некоторый конечный автомат Уотсона–Крика.
Теорема 5.4. Каждый язык L ∈ RE может быть представ-
лен в виде L = h(L
0
), где L
0
∈ AWK(u) и h — некоторая про-
екция.
Доказательство. Используя представление из теоремы 3.16,
запишем L = h
h
1
EQ(h
1
, h
2
)
∩R
0
, где h — проекция, h
1
, h
2
:
V
∗
1
−→ V
∗
2
— λ-свободные морфизмы, и R
0
⊆ V
∗
2
— регулярный
язык. Пусть M
0
= (K, V
2
, s
0
, F, δ) — такой детерминированный
конечный автомат, ч то R
0
= L(M
0
). Достаточно сконструиро-
вать конечный автомат Уотсона–Крика M со свойством
L
u
(M) = h
1
EQ(h
1
, h
2
)
∩ R
0
.
В самом деле, определим конечный автомат Уотсона–Крика
M = (V
2
, ρ, K, s
0
, F, δ
0
), в котором
1. ρ = {(a, a) | a ∈ V
2
},
2. δ
0
(s,
h
1
(a)
h
2
(a)
) = {s
0
} при условии s, s
0
∈ K, a ∈ V
1
, и
s, h
1
(a)
`
∗
(s
0
, λ),
3. δ
0
(s,
u
v
) = ∅ в про тивн ом случае.
(Символ `
∗
обозначает переход в автомате M
0
в смысле, опи-
санном в главе 3.) Теперь, как и в лемме 5.16, видно, что авто-
мат M обладает требуемым свойством.
Хотя кажется, что результат, подобный лемме 5.16, не ве-
рен для семейства F SWK(u), результат, подобный теореме 5.3,
остается верным и для этого семейства.
Теорема 5.5. Каждый язык L ∈ RE может быть представ-
лен в виде L = h(L
0
∩ R), где L
0
∈ F SWK(u), R ∈ REG, и h —
некоторая проекция.
Доказательство. Используя теорему 3.16, можно представить
L как L = h
h
1
EQ(h
1
, h
2
)
∩ R
0
, где h — проекция, h
1
, h
2
—
λ-свободные морфизмы, и R
0
— регулярный язык. Для h
1
, h
2
:
V
∗
1
−→ V
∗
2
, построим простой всефинальный автомат Уотсона–
Крика M = (V, ρ, K, s
0
, K, δ), в котором

212 5. Автоматы Уотсона–Крика
1. V = V
2
∪ {c},
2. ρ = {(a, a) | a ∈ V
2
} ∪ {(c, c)},
3. K = {s
0
, s
1
} ∪ {s
a
| a ∈ V
1
},
4. δ(s
0
,
h
1
(a)
λ
) = {s
a
},
5. δ(s
a
,
λ
h
2
(a)
) = {s
0
}, a ∈ V
1
,
6. δ(s
0
,
c
λ
) = {s
1
},
7. δ(s
1
,
λ
c
) = {s
1
} и
8. δ(s,
u
v
) = ∅ во всех других случаях.
Очевидно, что дл я регулярного языка R
1
= V
∗
2
{c} выпол-
няется равенство L
u
(M) ∩ R
1
= h
1
EQ(h
1
, h
2
)
{c}. (Сначала
чередование состояний s
0
, s
a
, а затем, после первого появления
состояния s
1
, его сохранение гарантирует то, что принимаемая
автоматом молекула имеет вид
h
h
1
(x)c
h
2
(x)c
i
для некоторого x ∈ V
∗
1
.)
Рассматривая R = R
0
{c} и дополняя проекцию h равен-
ством h(c) = λ, получаем L = h(L
u
(M) ∩ R).
Разумеется, проектирование h и пересечение с регулярным
языком R в теоремах 5.3 и 5.5 можно сделать с помощью детер-
минированной ОПМ, поэтому результат, подобный теореме 5.1,
остается верен и для семейств NW K(u) и F SWK(u).
Следовательно, можно сказать, что по модулю детермини-
рованной ОПМ, а в некоторых случаях и только по модулю
слабого кодирования, все семейства XWK(α), X ∈ {A, N, S, 1,
F, F S}, совпадают с RE , а значит, и межд у собой. Это приво-
дит к следующей оценке размеров этих семейств.
Следствие 5.7. Для каждого такого семейства языков FL,
что F L ⊂ RE и FL замкнуто относительно пересечения с ре-
гулярными языками и произвольных морфизмов, выполняется
XWK(u) − F L 6= ∅, X ∈ {A, S, F, 1, N, F S}.
Среди важных семейств языков F L, удовлетворяющих
посылке утверждения следствия 5.7, оказываются семей-
ства MAT
λ
и ET 0L.

5.4. Конечные преобразователи Уотсона–Крика 213
Отметим, что в предыдущих результатах заключительные
состояния роли не играли, так как они нисколько не увеличи-
вают порождающую силу конечных автоматов Уотсона–Крика
по модулю детерминированной ОПМ или в некоторых случаях
по модулю слабого кодирования. Кроме того, отметим, что про-
стых конечных автоматов Уотсона–Крика (всего лишь с тремя
состояниями) достаточно для характеризации RE по модулю
слабого кодирования. Автоматы без состояний, использующие
переходные пары
u
v
без дополнительных ограничений, нало-
женных на строки u, v, также оч ень сильны. Эти наблюдения
вновь и ллюстри руют мощь комплементарности Уотсона–Кри-
ка и они еще подтвердятся ниже пр и рассмотрении других уст-
ройств.
Стоит также упомянуть, что в большинстве приведен-
ных выше конструкций (имеются в виду доказательства
теоремы 5.5 и лемм 5.14 и 5.16) в качестве отношения ком-
плементарности бралось отношение равенства, т. е. (a, b) ∈ ρ
означало a = b. Это не относится к доказательству теоре-
мы 4.12, а значит, и к теореме 5.2. Как уже неоднократно
отмечалось, в молекуле ДНК отношение комплементарности
взаимно однозначно. Поэтому если мы пытаемся следовать
«реалиям ДНК», то мы долж ны считать основное отноше-
ние комплементарности для наших моделей симметричным и
взаимно однозначным. Из-за этого могут возникнуть некото-
рые проблемы, поскольку в доказательстве теоремы 4.12 уже
было использовано отношение, не являющееся даже инъектив-
ным: (s, s) ∈ ρ и в то же время
s, [s, k]
∈ ρ.
5.4 Конечные преобразователи Уотсона–Крика
Выходную последовательность можно связать с конечным
автоматом Уотсона–Крика тем же способом, каким такая
последовательность связывается с конечным автоматом в
виде ОПМ. Выходная посл едова тельн ость записывается на
обычной ленте, в отличие от вход ной, записанной на двойной
ленте Уотсона–Крика (иная возможность будет рассмотрена в
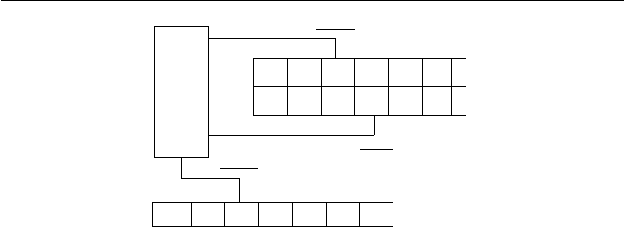
разделе 5.6). Рис. 5.4 иллюстрирует эту идею.
214 5. Автоматы Уотсона–Крика
s
?
?
-
6
-
-
Рис. 5.4. Преобразователь Уотсона–Крика.
ОПМ Уотсона–Крика — это конструкция
g = (V
I
, ρ
I
, V
O
, K, s
0
, F, δ),
в которой
1. V
I
— входной алфавит,
2. ρ
I
⊆ V
I
× V
I
— симметри чно е отношение (комплементарно-
сти),
3. V
O
— выходной алфавит,
4. K — множество состояний,
5. s
0
∈ K — начальное состояние,
6. F ⊆ K — множество заключительных состояний и
7. δ : K ×
V
∗
I
V
∗
I
−→ P
f
(V
∗
O
× K) — такое отображение, что
δ(s,
u
v
) 6= ∅ лишь для конечного чи сла троек (s, u, v) ∈
K × V
∗
I
× V
∗
I
.
Соотношение (x, s
0
) ∈ δ(s,
u
v
) интерпретируется так: нахо-
дясь в состоянии s, преобразователь прочитывает u на верхней
дорожке и v на нижней дорожке сдвоенной ленты, пишет на
выходной ленте x, и переходит в состояние s
0
.
Более формально, для w
1
, w
2
, w
0
1
, w
0
2
∈ V
∗
I
, x, z ∈ V
∗
O
, и
s, s
0
∈ K, пишем
zs
w
1
w
2
=⇒ zxs
0
w
0
1
w
0
2

5.4. Конечные преобразователи Уотсона–Крика 215
тогда и только тогда, когда w
1
= x
1
w
0
1
, w
2
= x
2
w
0
2
, для (x, s
0
) ∈
δ(s,
x
1
x
2
), x
1
, x
2
, w
0
1
, w
0
2
∈ V
∗
I
. Для последовательности w =
h
w
1
w
2
i
∈ WK
ρ
I
(V
I
) определим
g(w) =
z ∈ V
∗
O
| s
0
w
1
w
2
=⇒
∗
zs
f
λ
λ
, s
f
∈ F
.
Распространение этого определения на языки из WK
ρ
I
(V
I
) про-
изводится как обычно.
Как и для конечных автоматов Уотсона–Крика, рассмот-
рим ОПМ Уотсона–Крика без состояний, простые, 1-ограни-
ченные, всефинальные ОПМ Уотсона–Крика и четыре их по-
парные комбинации.
Следующий результат получается из леммы 5.14 из-за то-
го, что помечивание переходов в конечном автомате Уотсона–
Крика без состояний можно выразить через выходную функ-
цию ОПМ Уотсона–Крика.
Следствие 5.8 . Для каждого алфавита V существует та-
кая 1-ограниченная ОПМ Уотсона–Крика без состояний, что
выполняется ра венство T S
V
= g
V
WK
ρ
(V )
для ρ = {(a, a) |
a ∈ V }.
Это влечет результат, подобный теор еме 5.1: каждый язык
L ∈ RE можно представить в виде L = g
g
V
WK
ρ
(V )
, где
g — обычная детерминированная ОПМ, а g
V
— 1-ограниченная
ОПМ Уотсона–Крика без состояний.
И пересечение с регулярным языком, и морфизм реализу-
ются посредством ОПМ Уотсона–Крика, следовательно, по тео-
реме 5.5 получаем:
Теорема 5.6. Для каждого языка L ∈ RE, L ⊆ V
∗
, существу-
ет такая простая всефинальная ОПМ Уотсона–Крика, что
L = g
L
WK
ρ
(V
0
)
для некоторой области Уотсона–Крика
WK
ρ
(V
0
).
Следовательно, конечные преобразователи Уотсона–Крика
не только не сохраняют на месте семейства из иерархии Хом-

216 5. Автоматы Уотсона–Крика
ского, но даже отображают (очень простые) регулярные языки
так, что их образы покрывают все семейство RE .
Аналогично тому, что каждый двухголовочный конеч-
ный автомат можно считать вариантом конечного автомата
Уотсона–Крика, двухголовочный конечный преобразователь
можно рассматривать как частный случай ОПМ Уотсона–
Крика.
5.5 Дальнейшие варианты конечных автоматов
Уотсона–Крика
Среди конечных автоматов Уотсона–Крика, рассмотренных в
разделе 5.1, наиболее близко связанными с процессами в струк-
турах ДНК являются автоматы без состояний, которые при
работе используют лишь комплементарность Уотсона–Крика и
не обладают никакими другими возможностями в духе теории
автоматов. Эти автоматы заслуживают дополнительного изу-
чения.
Из леммы 5.11 и равенства h(w
1
w
2
) = h(w
1
)h(w
2
), где h —
морфизм, следует, что невозможно представить каждый ре-
гулярный язык как образ при морфизме языка из NWK(α),
α ∈ {u, ctr}. Следовательно, с одной стороны, на этой основе
нельзя получить даже представления всех регулярных языков,
с другой стороны, результаты теорем 5.1 и 5.5 н ельзя улуч-
шить, заменив детерминированные ОПМ отображения на мор-
физмы или отказавшись от использования пересечения с регу-
лярными языками.
«Слабым местом» конечных автоматов Уотсона–Крика без
состояний является неспособность контролировать первый шаг
вычисления. Это наводит на мысль о следующем определении.
Инициальный конечный автомат Уотсона–Крика без со-
стояний — это четверка
M = (V, ρ, P
0
, P ),
в которой V — алфавит, ρ ⊆ V ×V — симметричное отношение,
P
0
и P — конечные подмножества множества
V
∗
V
∗
.

5.5. Варианты автоматов Уотсона–Крика 217
Двойная цепочка
h
w
1
w
2
i
∈ WK
ρ
(V ) распознается автома-
том M тогда и только тогда, когда
w
1
= x
0
x
1
. . . x
n
, w
2
= y
0
y
1
. . . y
n
, n > 0,
где
x
0
y
0
∈ P
0
,
x
i
y
i
∈ P, 1 6 i 6 n.
Иначе говоря, в начале разбора строки
h
w
1
w
2
i
следует использо-
вать элемент из P
0
, а затем элементы из P
0
лишь в том случае,
когда P
0
∩ P 6= ∅.
Как обычно, обозначим через L
α
(M), α ∈ {u, cr t} язы-
ки, ассоциированн ые с корректными вычислениями в M. Че-
рез INWK(α), IN SWK(α) обозначим семейства языков, рас-
познаваемых инициальными конечными автоматами Уотсона–
Крика без состояний и простыми инициальными конечными
автоматами Уотсона–Крика без состояний соответственно.
Как и следовало ожидать, установив контроль за первым
шагом процесса распознавания мы увеличили силу наших уст-
ройств. Тем не менее, легко видеть, что результат подобный
лемме 5.9, по-прежнему верен:
Лемма 5.17. INSWK(u) ⊆ REG .
С другой стороны, появился результат, не имевший аналога
для неинициальных автоматов.
Теорема 5.7. Каждый регулярный язык является кодирова-
нием некоторого языка из семейства INSWK(u).
Доказательство. Рассмотрим детерминированный конечный
автомат M = (K, V, s
0
, F, δ) и построим инициальный простой
конечный автомат Уотсона–Крика без состояний
M
0
= (U, ρ, P
0
, P ),
в котором
1. U = {[s, a, s
0
]
i
| s, s
0
∈ K, a ∈ V, 1 6 i 6 4},
2. ρ = {([s, a, s
0
]
i
, [s, a, s
0
]
i
) | s, s
0
∈ K, a ∈ V, 1 6 i 6 4},

218 5. Автоматы Уотсона–Крика
3. P
0
=
n
[s
0
,a,s
0
]
1
λ
| s
0
= δ(s
0
, a), a ∈ V
o
∪
n
[s
0
,a,s
0
]
3
λ
| s
0
= δ(s
0
, a) ∈ F, a ∈ V
o
,
4. P =
n
[s,a
1
,s
0
]
2
[s
0
,a
2
,s
00
]
1
λ
| s
0
= δ(s, a
1
), s
00
= δ(s
0
, a
2
),
s, s
0
, s
00
∈ K, a
1
, a
2
∈ V
o
∪
n
[s,a
1
,s
0
]
2
[s
0
,a
2
,s
00
]
3
λ
| s
0
= δ(s, a
1
),
s
00
= δ(s
0
, a
2
), s, s
0
∈ K, s
00
∈ F, a
1
, a
2
∈ V
o
∪
n
[s,a,s
0
]
4
λ
| s
0
= δ(s, a) ∈ F, s ∈ K, a ∈ V
o
∪
n
λ
[s,a
1
,s
0
]
1
[s
0
,a
2
,s
00
]
2
| s
0
= δ(s, a
1
), s
00
= δ(s
0
, a
2
),
s, s
0
, s
00
∈ K, a
1
, a
2
∈ V
o
∪
n
λ
[s,a
1
,s
0
]
1
[s
0
,a
2
,s
00
]
4
| s
0
= δ(s, a
1
),
s
00
= δ(s
0
, a
2
) ∈ F, s, s
0
∈ K, s
00
∈ F, a
1
, a
2
∈ V
o
∪
n
λ
[s,a,s
0
]
3
| s
0
= δ(s, a) ∈ F, s ∈ K, a ∈ V
o
.
Каждое распознавание последовательности должно начи-
наться с
[s
0
,a,s
1
]
1
λ
из P
0
, за исключением распознавания по-
следовательности длины один, которое начинается с
[s
0
,a,s
1
]
3
λ
из P
0
и немедленно заканчивается после применения
λ
[s
0
,a,s
1
]
3
из P . Нить x в каждом элементе из P вида
x
λ
начинается либо
с символ а [s, a, s
0
]
2
, л ибо с символа [s, a, s
0
]
4
. Ни ть y в каждом
элементе из P вида
λ
y
начинается либо с символа [s, a, s
0
]
1
,
либо с символа [s, a, s
0
]
3
. Следовательно, после завершения раз-
бора элемента из WK
ρ
(U) никакой лишний шаг уже невозмо-
жен из-за отсутствия допустимых комплементарных пар.
Это означает, что успешно перерабатываются лишь после-
довательности w ∈ WK
ρ
(U), составленные из двух одинаковых
цепочек вида
[s
0
, a
1
, s
1
]
1
[s
1
, a
2
, s
2
]
2
[s
2
, a
3
, s
3
]
1
[s
3
, a
4
, s
4
]
2
. . . [s
k−1
, a
k
, s
k
]
i
[s
k
, a
k+1
, s
k+1
]
j
,
в которых i = 2, j = 3 при четном k и i = 1, j = 4 при нечет-
ном k; причем s
0
s
1
. . . s
k+1
является последовательностью со-
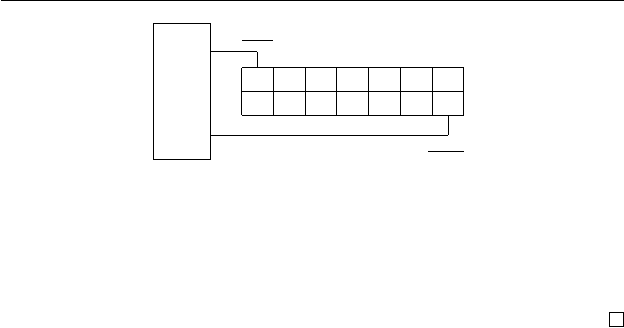
5.5. Варианты автоматов Уотсона–Крика 219
s
0
?
-
6
Рис. 5.5. Реверсивный конечный автомат Уотсона–Крика.
стояний, соответствующей процессу распознавания строки a
1
a
2
. . . a
k+1
из M.
Пусть h — такое кодирование, которое отображает тройку
[s, a, s
0
]
i
в a. Тогда получим L(M ) = h
L
u
(M
0
)
.
Поскольку каждый обыкновенный конечный автомат Уо т-
сона–Крика без состояний можно рассматривать как иници-
альный, считая P
0
= P , получаем включение XWK(α) ⊆
IXWK(α), X ∈ {N, NS}, α ∈ {u, ctr}. Следовательно, харак-
теризации семейства RE из теорем 5.1 и 5.3 остаются верными
и для соответствующих семейств IXWK(α), α ∈ {u, ctr}.
Как мы знаем из главы 1, две цепочки молекулы ДНК име-
ют противоположные 5
0
−3
0
-ориентации. Это наводит на мысль
рассмотреть такой вариант конечного автомата Уо тсона– Кри-
ка, который производит разбор двух дорожек ленты Уотсона–
Крика в прот ивоп оложных направлениях. Рис. 5.5 показывает
начальную конфигурацию такого автомата.
Более формально, реверсивный конечный автомат Уотсо-
на–Крика — это конструкция
M = (V, ρ, K, s
0
, F, δ),
компоненты которой определяются также как и у конечных ав-
томатов Уотсона–Крика, а отношение выводимости =⇒ опреде-
ляется следующим образом: для w
1
, w
2
, w
0
1
, w
0
2
, x, y ∈ V
∗
, s, s
0
∈
K, пишем
w
1
w
2
y
s
xw
0
1
w
0
2
=⇒
w
1
x
w
2
s
0
w
0
1
yw
0
2

220 5. Автоматы Уотсона–Крика
тогда и только тогда, когда
w
1
xw
0
1
w
2
yw
0
2
∈ WK
ρ
(V ), s
0
∈ δ(s,
x
y
).
При этом последовательность
h
w
1
w
2
i
∈ WK
ρ
(V ) распознается
автоматом M тогда и только тогда, когда
λ
w
2
s
0
w
1
λ
=⇒
∗
w
1
λ
s
f
λ
w
2
, для s
f
∈ F.
Как и в разделе 5.1, с ревер сивн ым конечным ав тома-
том Уотсона–Крика M можно связать два языка L
α
(M),
α ∈ {u, ctr}. Соответствующие XWK(α) семейства языков,
ассоциированных с реверсивными конечными ав томатами Уот-
сона–Крика, обозначим через XRWK(α), X ∈ {A, N, F, S, 1,
NS, N1, F S, F 1}.
Ясно, что диаграмма, подобная той, что изображена на
рис. 5.2, может быть составлена и для этих семейств.
В простых автоматах без состояний существенным является
не направление движения головок, а возможность покрытия
поданной на вход двойной цепочки блоками верхней и нижней
дорожек. Отсюда следует
Лемма 5.18. N SWK(u) = NSRWK(u).
Используя теперь лемму 5.9, получим
Следствие 5. 9. NSRWK(u) ⊆ REG.
Для новой конструкции будет верен и аналог теоремы 5.1.
Лемма 5.19. Для каждого алфавита V выполняется RT S
V
∈
N1RWK(ctr).
Доказательство. Взяв 1-ограниченный автомат Уотсона–Кри-
ка M из доказательства леммы 5.14 и, проинтерпретировав его
как реверсивный автомат, получим L
ctr
(M) = RT S
V
.
Теорема 5.8. Каждый рекурсивно перечислимый язык яв-
ляется образом при детерминированном ОПМ-отображе-
нии некоторого языка любого из семейств XRWK(ctr),
X ∈ {A, N, F, S, 1, NS, N1, F S, F 1}.
