Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений

Подождите немного. Документ загружается.

5.2. Соотношения между WK-семействами 201

Для каждого правила перехода

t : s



. . . a

. . . b



→



. . . a

. . . b



из P , n > 0, m > 0, n + m > 2, занесем в P

правила





→





t,1

t,i



i+1



→



i+1



t,i+1

, 1 6 i 6 n − 1,

t,n





→





t,1

t,i



i+1



→



i+1



t,i+1

, 1 6 i 6 m − 2,

t,m−1





→





Кроме того, поместим все состояния s

t,i

, s

t,i

в K

в дополнение

ко всем состояниям из K.

Легко видеть, что получившийся автомат эквивалентен M

и 1-огран ичен , а новые состояния контролируют работу M

де-

терминированным образом.

Следствие 5. 1. 1WK(u) = SWK(u) = AWK(u).

Приведенная выше конструкция изменяет язык L

ctr

(M).

Нам не известно, справедливо ли включени е, аналогичн ое

включению из леммы 5.7 и для семейств 1WK(ctr), SWK(ctr),

AWK(ctr).

Для удобства ссылок мы суммируем соотношения из преды-

дущих лемм для семейств XWK(ctr) в диаграмме на рис. 5.2.

Стрелки на нем означают включения, возможно и нестрогие.

Случай семейств XWK(u) отложим до установления допол ни -

тельных соотношений между ними.

Замечание 5.4. Определ енные выше устройства приводят к

понятию двухголовочных конечных автоматов.

Двухголовочный конечный автомат представляет собой

конструкцию M = (K, V, s

, F, δ), в которой K, V, s

, F имеют

обычный для конечного автомата смысл, δ — функция пере-

202 5. Автоматы Уотсона–Крика

N1WK(ctr)









NSW K(ctr)F 1W K(ctr)





F SW K(ctr) NW K(ctr)





F W K(ctr)

1W K(ctr)

SW K(ctr)

AW K(ctr)









Рис. 5.2. Иерархия ctr-семейств.

хода, δ : K × (V ∪ {λ}) × (V ∪ {λ}) −→ P(K). Для w

, w

, x

∈ V

∗

, u

∈ V ∪ {λ} и s, s

∈ K пишем

, w

)s(u

, u

) =⇒ (w

, w

, x

)

тогда и только тогда, когда s

∈ δ(s, u

, u

). Язык, распознава-

емый M, определяется как

L(M) = {x ∈ V

∗

| s

(x, x) =⇒

∗

(x, x)s

, s

∈ F }.

Обозначим через T H семейство языков, распознаваемых таки-

ми автоматами.

Интенсивно исследуются и некоторые другие разнов идн о-

сти двухголовочных (или более общо, многоголовочных) ко-

нечных автоматов: в частности, детерминированные, простые

(одна головка читает ленту, а остальные различают на входной

строке лишь маркеры конца), ощущающие (голов ки «ощуща-

ют», когда две из них располагаются напротив одной и той же

ячейки ленты). Точные определения, результаты и дальнейшие

ссылки можно найти в [77, 146, 151, 288].

5.2. Соотношения между WK-семействами 203

Очевидно, что двухголовочный конечный автомат есть

частный случай 1-ограниченного конечного автомата Уотсо-

на–Крика, когда в качестве отношения комплементарности

берется отношение равенства: (a, b) ∈ ρ тогда и только тогда,

когда a = b. С другой стороны, 1-ограниченный конечный

автомат Уотсона–Крика можно смоделировать при помощи

двухголовочного конечного автомата: первая головка разби-

рает входную строку, действуя как верхняя головка автомата

Уотсона–Крика, а вторая разбирает ту же строку, действуя

как нижняя головка автомата Уотсона–Крика, при этом

предполагается, что проход верхней головки через символ a

осуществляется только при условии, что нижняя в том же

состоянии автомата проходит комплементарный ему символ b.

Тем самым получаем следующее равенство:

Лемма 5.8. T H = 1WK(u).

Конечный автомат Уотсона–Крика можно рассматривать и

как двухленточный двухголовоч ный конечный автомат специ-

ального типа, в котором ленты связаны отн ошением компле-

ментарности. В случае молекулы ДНК такое отношение взаим-

но-однозначно, т. е. одна лента в точности определяет вторую.

В случае простого автомата без состояний при разборе стр о-

ки из WK

(V ) достаточно проверить подпоследовательность

длиной не более максимума дли н строк w

, w

из правил пере-

хода





. Причина этого в том, что одна из строк w

и w

обя-

зательно пустая, и поэтому можно действовать на том уровне,

у которого читающая головка оказалась позади другой, тем

самым ограни чива я дистанцию между двумя головками (за-

держку). Отсюда вытекает

Лемма 5.9. NSWK(u) ⊆ REG .

Справедливо следующее усиление леммы 5.4.

Лемма 5.10. REG ⊆ F 1WK(u).

Доказательство. Рассмотрим конечный автомат M = (K, V,

, F, δ) и построим всефинальный 1-ограниченный конечный

204 5. Автоматы Уотсона–Крика

автомат Уотсона–Крика

= (V, ρ, K

, s

, K

, δ

в котором

ρ = {(a, a)) | a ∈ V },

= K ∪ {s

}, (s

/∈ K),

(s,





) = δ(s, a) ∪ F (s, a),

где s ∈ K, a ∈ V , F (s, a) =

(

}, если δ(s, a) ∩ F 6= ∅,

∅ в противном случае,





) = {s

}, a ∈ V,

(s,





) = ∅ во всех других случаях.

Распознавание последовательности





происходит так.

Сначала слева направо читается первая строка точно также

как и в M, за исключением последнего шага, на котором M

переходит в заключительное состояние, а M

переходит в состо-

яние s

. Затем читается вторая строка и последовательность

либо принимается, либо отвергается.

Следовательно, L

) = L(M).

Теперь все соотношения между семействами XWK(u) мож-

но собрать на одной диаграмме, показанной на рис. 5.3. Как

обычно, стрелки означают не обязательно строгие включения.

Семейства XWK(u) «малы» в том смысле, что языки этих

семейств удовлетворяют очень сильным условиям. В следую-

щих леммах приведены два таких необходимых условия.

Лемма 5.11. (i) Если L ∈ NWK(α) для α ∈ {u, ctr}, то L =

(ii) Если L ∈ N1WK(u), то найдется такой алфавит V,

что L = V

Доказательство. (i) Рассмотрим конечный автомат Уотсона–

Крика без состояний M = (V, ρ, P ). Если w

, w

∈ WK

(V )

можно разобрать с помощью правил из P , то и w

тоже

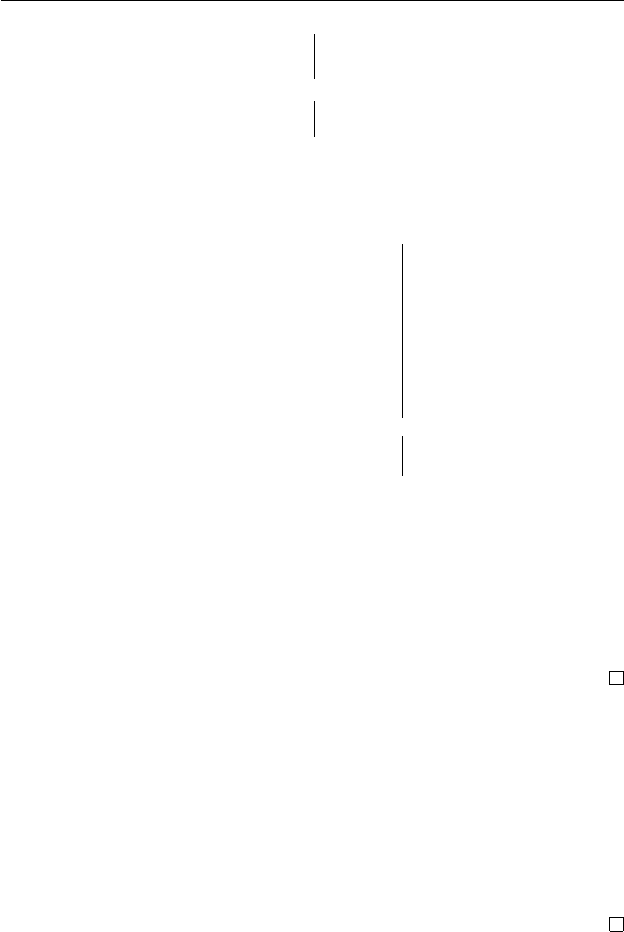
5.2. Соотношения между WK-семействами 205

NSW K(u)

N1WK(u)

REG

F 1W K(u)

F SW K(u) N W K(u)



3

F W K(u)

AW K(u) = SW K(u) = 1W K(u)

Рис. 5.3. Иерархия u-семейств.

можно разобрать с помощью тех же правил. Следовательно,

(M)

⊆ L

(M), α ∈ {u, ctr}. Противоположное включение,

(M) ⊆ L

(M)

, очевидно.

(ii) Очевидно, поскольку каждая строка распознается 1-

ограниченным автоматом Уотсона–Крика без состояний.

Ниже (лемма 5.14) будет видно, что утверждение (ii) не вер-

но для ctr-случая.

Следствие 5.2. REG − XWK(α) 6= ∅, α ∈ {u, ctr}, X ∈

{N, NS}.

Следствие 5. 3. F 1WK(u) − N WK(u) 6= ∅.

Доказательство. По лемме 5.10 язык ab

∗

лежит в F 1WK(u).

Но этот язык не обладает свойством из пункта (i) леммы 5.11,

значит, ab

∗

/∈ NWK(u).

Следствие 5.4. Включение NWK(u) ⊂ F WK(u) и включение

NSWK(u) ⊂ F 1WK(u) являются строгими.

206 5. Автоматы Уотсона–Крика

Лемма 5.12. Каждый язык из AWK(u) над однобуквенным

алфавитом регулярен.

Доказательство. Рассмотрим конечный автомат Уотсона–

Крика без дополнительных ограничений M = (V, ρ, K, s

, F, δ).

Если есть переход s

∈ δ(s,





), в котором слово w содержит

букву b и (a, b) /∈ ρ, то этот переход можно не использовать

при выработке строк из L

(M). Таким образом, обо всех таких

переходах можно забыть и считать, что все вышеупомянутые

буквы b обладают свойством (a, b) ∈ ρ. Построим ли ней ную

грамматику G = (K, {a, b}, s

, P ), в которой

P =



s → a

| s

∈ δ(s,





), s, s

∈ K, i > 0, j = |w|



∪



s → a

| δ(s,





) ∩ F 6= ∅, s ∈ K, i > 0, j = |w|



Кроме того, рассмотрим линейный язык L = {a

| n > 1}.

По следствию 5.3.1 из [115], L(G) ∩ L — линейный язык.

L(G) ∩ L =



| (n, m) ∈ Ψ

{a,b}



L(G)



∩ {(p, p) | p ∈ N}



Из того, что пересечение двух полулинейных множеств явля-

ется полулинейным, следует полулинейность множества

{a,b}



L(G) ∩ L



А это, вместе с вышеупомянутым результатом из [115], влечет

линейность языка L(G) ∩ L.) Определив слабое кодирование h

как h(a) = a, h(b) = λ, получим равенство

(M) = h



L(G) ∩ L



из которого следует, что L

(M) регулярен.

Следствие 5. 5. Включение AWK(u) ⊂ CS строгое.

Однако обсуждавшиеся выше семейства (за исключением

NSWK(u)) содержат языки очень большой сложности. В сле-

дующем разделе будет показано, что на их основе с исполь-

зованием AFL-операций (слабого кодирования и детерминиро-

ванных ОПМ) можно получить характеризацию рекурсивно

перечислимых языков. Завершает текущий раздел результат,

5.2. Соотношения между WK-семействами 207

прямо доказывающий, что конечные автоматы Уотсона–Крика

без состояний способны распознавать сложные языки. Конеч-

но, причиной этого является использование двойных цепочек.

Лемма 5.13. N WK(u) − MAT

6= ∅.

Доказательство. Рассмотрим конечный автомат Уотсона–

Крика без состояний M = ({a, b, c, d, e, f }, ρ, P ), в котором

ρ = {(a, a), (b, c), (c, b), (a, d), (d, a), (e, f ), (f, e)} ,

P =



































Кроме того, рассмотрим регулярный язык, описываемый сле-

дующим регулярным выражением:

R = c(dd

b)(aa

и слабое кодирование h, определяемое равенствами

h(a) = a, h(b) = h(c) = h(d) = h(e) = λ.

Распознаваемые M молекулы, у которых в верхней нити рас-

полагается строка из R, должны иметь вид



b . . . ba

m−1

m+1

b x

c x

c . . . c x

m−1

c x

m+1



где m > 3, n

> 2, 1 6 i 6 m, n

m+1

> 1. Вдобавок из-за

комплементарности выполняется x

= a

, x

∈ {a, d}

∗

, |x

| =

для 2 6 i 6 m.

По виду множества P каждое появление b в верхней цеп оч-

ке сочетается с появлением в нижней либо b, ли бо c, на что

указывают индексы у символов b, c в следующей записи



. . . b

m−2

m−1

m+1

−1

. . . c

m−1

f f

m+1

−1



Последнее вхождение c в нижнюю цепочку находится в паре с

первым вхождением e в верхнюю.

Теперь, с учетом точного распределения по парам, и по-

скольку символы a появляются лишь парами





из P , а симво-

лы d в нижней строке появляются лишь из пар





, получаем,

208 5. Автоматы Уотсона–Крика

что

∈ a

, 2 6 i 6 m − 1,

= d

m+1

−1

| = n

i+1

, 1 6 i 6 m − 1.

Из |x

| = n

и |x

| = n

i+1

получим n

= n

i+1

, 1 6 i 6 m − 1.

Значит, распознанная молекула имеет вид



b . . . ba

n+1

c . . . ca

n+1



где не менее двух блоков ba

и n > 2.

Следовательно,



(M) ∩ R



= {a

| n, m > 2}

= {a

| p — составное число}.

Этот язык не полулинеен, а значит, не регулярен. Каждый

язык из MAT

над однобуквенным алфавитом регулярен [129].

Семейство MAT

замкнуто относительно пересечений с регу-

лярными языками и произв ольн ых морфизмов. Следователь-

но, L

(M) /∈ MAT

Следствие 5. 6. Включение N SWK(u ) ⊂ NWK(u) строгое.

5.3 Характеризации рекурсивно перечислимых

языков

Теперь приведем ряд результатов о представлении рекурсив-

но перечислимых языков с помощью языков, распознаваемых

конечными автоматами Уотсона–Крика различных типов. Мы

характеризуем RE, поскольку RE замкнуто относительно при-

меняемых операций.

Доказательство следующей леммы, хотя и просто техниче-

ски, существенно опирается на свойства лент Уотсона–Крика

и на взаимосвязь с языками перетасованных копий.

Лемма 5.14. Для каждого алфавита V выполняется T S

∈

N1WK(ctr).

5.3. Характеризации RE языков 209

Доказательство. Рассмотрим 1-ограниченный конечный ав-

томат Уотсона–Крика M = (V, ρ, P ), в котором ρ = {(a, a) |

a ∈ V }, P = {









| a ∈ V }, и помечивание e(





) = a,





) = ¯a, a ∈ V .

Если





∈ WK

(V ) и σ : s





=⇒

∗





есть некоторое

вычисление в M (состояние s

выписано только для того, что-

бы показать, что вычисление нетривиально), то e(σ) ∈ x t⊥ ¯x,

поэтому e(σ) ∈ T S

Поскольку в качестве x можно взять любую строку из V

∗

, и

каждый элемент x t⊥ ¯x описывает корректное вычисление в M,

получаем равенство L

ctr

(M) = T S

Теорема 5.1. Каждый язык в семействе RE является обра-

зом детерминированного ОПМ отображения некоторого язы-

ка любого из семейств XWK(ctr), X ∈ {A, N, F, S, 1, NS , N 1,

F S, F 1}.

Доказательство. Это непосредственное следствие предыду-

щей леммы и теоремы 3.17.

Лемма 5.15. SRSL(c) ⊆ F WK(u).

Доказательство. Рассмотрим простую регулярную склеиваю-

щую систему γ = (V, ρ, A, D

, D

), в которой элементы из D

помечены функцией e : D

∪ D

−→ Lab.

Построим всефинальный конечный автомат Уотсона–Кри-

ка M = (V, ρ, {s

, s

}, s

, {s

, s

}, P ) , с правилами перехода

1. s





→





для

i



∈ A,

∈ WK

(V ),





∈



∗



∪



∗



2. s





→





для таких





∈ D





∈ D

, что





) = e(





Соответствующее корректное вычисление в γ можно смо-

делировать с помощью корректного вычисления в M и об-

ратно, последовательность, распознаваемая автоматом M так-

же строится и при корректном (соответствующем) вычисле-

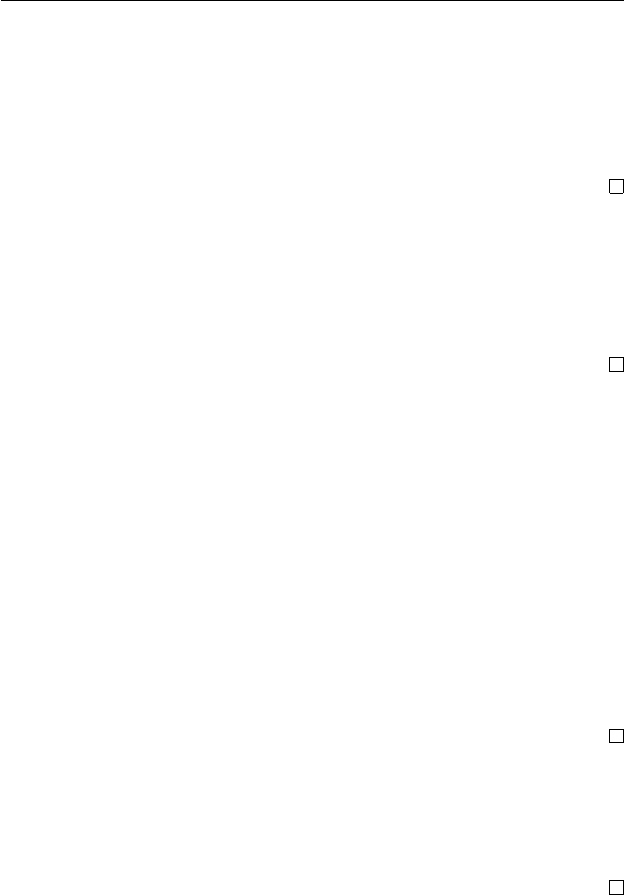
210 5. Автоматы Уотсона–Крика

нии в γ. Действительно, начало процесса вывода с аксиомы

гарантируется списком правил, содержащих начальное состоя-

ние s

, а соответствие вычислений обеспечивается правилами

перехода, которые определяются только такими парами





что





∈ D





∈ D

, и эти два блока одинаково помечены.

Следовательно, L

(γ) = L

(M).

Теорема 5.2. Каждый рекурсивно перечислимый язык явля-

ется слабым кодированием языка из семейства XWK(u), X ∈

{A, F, S, 1}.

Доказательство. Данное утверждение следует из леммы 5.15,

включения F WK(u) ⊆ XWK(u), X ∈ {A, S, 1} (см. рис. 5.3), и

теоремы 4.12.

Лемма 5.16. Если h

, h

: V

∗

−→ V

∗

— два морфизма, то



EQ(h

, h

)



∈ NWK(u).

Доказательство. Для данных h

, h

построим конечный авто-

мат Уотсона–Крика без состояний M = (V

, ρ, P ), в котором

ρ = {(a, a) | a ∈ V

} , P =



(b)



| b ∈ V



Последовательность

∈ WK

) успешно воспринима-

ется автоматом M тогда и только тогда, когда w

= w

(бла-

годаря отношению ρ) и w

= h

(x), w

= h

(x), для неко-

торого x ∈ V

∗

(благодаря виду правил из P ). Следователь-

но, x ∈ EQ(h

, h

) и w

∈ h



EQ(h

, h

)



, из чего следует,

что L

(M) = h



EQ(h

, h

)



Теорема 5.3. Каждый язык L ∈ RE может быть представ-

лен в виде L = h(L

∩ R), где L

∈ N WK(u), R ∈ REG, и h —

некоторая проекция.

Доказательство. Это непосредственное следствие предыду-

щей леммы и теоремы 3.16.

Можно преобразовать теорему 5.3 в следующий возможно

более интересный результат: каждый рекурсивно перечисли-