Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

26 Measurement and Data Analysis for Engineering and Science

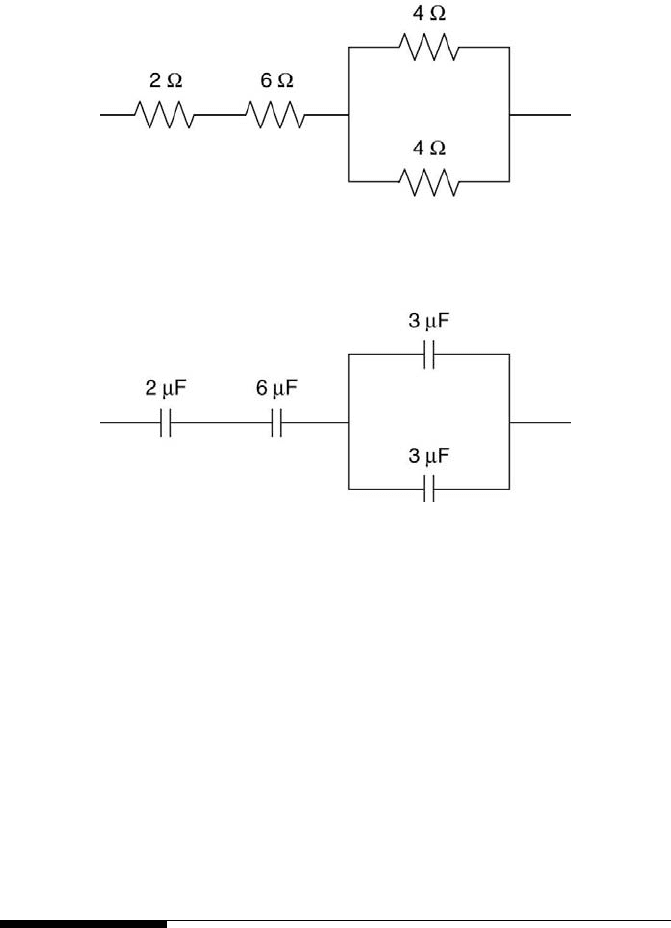
FIGURE 2.6

Parallel R, C, and L circuit conﬁgurations.

Thus, when in parallel, capacitances add, and the reciprocals of resistances

and inductances add.

Example Problem 2.2

Statement: Determine the total equivalent resistance, R

, and total equivalent

capacitance, C

, for the respective resistance and capacitance circuits shown in Figure

2.7.

Solution: For the two resistors in parallel, the equivalent resistance, R

, is

= 2 Ω.

The two other resistors are in series with R

, so R

= R

+ 2 + 6 = 10 Ω.

For the two capacitors in parallel, the equivalent capacitance, C

, is C

= 3 + 3 =

6 µF . This is in series with the two other capacitors, which implies that

= 1.

So, C

=1 µF.

To aid further with circuit analysis, two laws developed by G. R. Kirch-

hoﬀ (1824 - 1887) can be used. Kirchhoﬀ’s current (or ﬁrst) law, which

is conservation of charge, states that at any junction (node) in a circuit, the

current ﬂowing into the junction must equal the current ﬂowing out of it,

which implies that

node

out

. (2.15)

A node in a circuit is a point where two or more circuit elements meet.

Kirchhoﬀ’s voltage (or second) law, which is conservation of energy,

says that around any loop in a circuit, the sum of the potential diﬀerences

equals zero, which gives

Electronics 27

FIGURE 2.7

Resistor and capacitor circuits.

i,cl.loop

= 0. (2.16)

A loop is a closed path that goes from one node in a circuit back to it-

self without passing through any intermediate node more than once. Any

consistent sign convention will work when applying Kirchhoﬀ’s laws to a

circuit. Armed with this information, some important DC circuits can be

examined now.

2.5 Elementary DC Circuit Analysis

In DC circuits, current is steady in time. Thus, there is no inductance, even

if an inductor is present. An actual inductor, however, has resistance. This

typically is on the order of 10 Ω. Often, an inductor’s resistance in a DC

circuit is neglected.

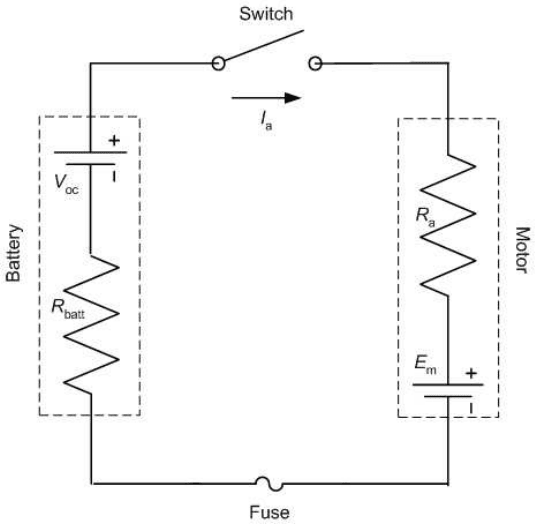
28 Measurement and Data Analysis for Engineering and Science

FIGURE 2.8

A battery and electric motor circuit.

The ﬁrst elementary DC circuit to analyze is that of a DC electric motor

in series with a battery, as shown in Figure 2.8. Examine the battery ﬁrst.

It has an internal resistance, R

batt

, and an open circuit voltage (potential

diﬀerence), V

. R

batt

is the resistance and V

the potential diﬀerence that

would be measured across the terminals of the battery if it were isolated

from the circuit by not being connected to it. However, when the battery is

placed in the circuit and the circuit switch is closed such that current, I

ﬂows around the circuit, the situation for the battery changes. The measured

potential diﬀerence across the battery now is less because current ﬂows

through the battery, eﬀectively leading to a potential diﬀerence across R

batt

This yields

batt

= V

− I

batt

, (2.17)

in which V

batt

represents the closed-circuit potential diﬀerence across the

battery. Similarly, the DC motor has an internal resistance, R

, which is

mainly across its armature. It also has an opposing potential diﬀerence,

, when operating with the battery connected to it. To summarize, V

measured across the battery terminals when the switch is open, and V

batt

measured when the switch is closed.

Electronics 29

Now what is E

in terms of the known quantities? To answer this, apply

Kirchhoﬀ’s second law around the circuit loop when the switch is closed.

Starting from the battery’s anode and moving in the direction of the current

around the loop, this gives

− I

batt

− E

− I

= 0, (2.18)

which immediately leads to

= V

− I

batt

+ R

). (2.19)

This equation reveals a simple fact: the relatively high battery and motor

internal resistances lead to a decrease in the motor’s maximum potential

diﬀerence. This consequently results in a decrease in the motor’s power

output to a device, such as the propeller of a remotely piloted aircraft.

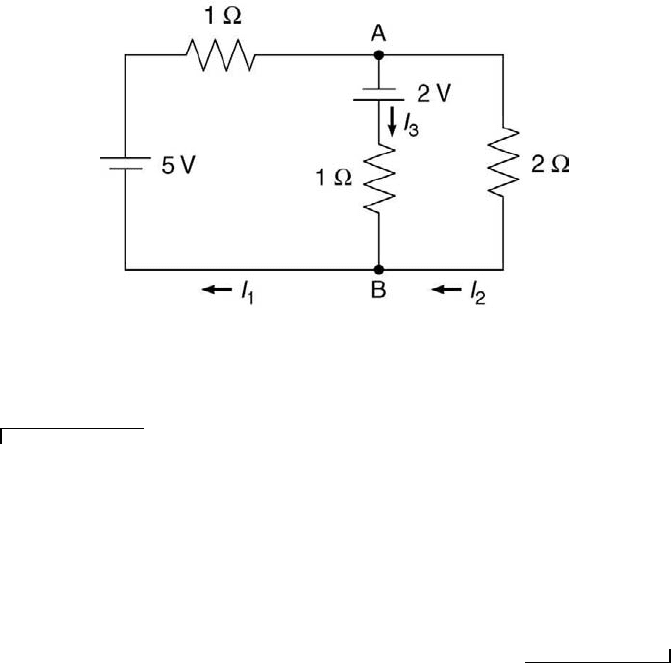
FIGURE 2.9

An electrical circuit.

Example Problem 2.3

Statement: For the electrical circuit shown in Figure 2.9, determine [a] the magni-

tude of the current in the branch between nodes A and B and [b] the direction of that

current.

Solution: Application of Kirchhoﬀ’s second law to the left loop gives 5 V − (1 Ω)(I

A) + 2 V − (1 Ω)(I

A) = 0. Similar application to the right loop yields 2 V − (2

Ω)(I

A) + (1 Ω)(I

A) = 0. At node A, application of Kirchhoﬀ’s ﬁrst law implies I

− I

= 0. These three expressions can be solved to yield I

= 3.8 A, I

= 0.6 A,

and I

= 3.2 A. Because I

is positive, the direction shown in Figure 2.9, from node A

to node B, is correct.

The second elementary direct-current circuit is a Wheatstone bridge.

The Wheatstone bridge is used in a variety of common instruments such

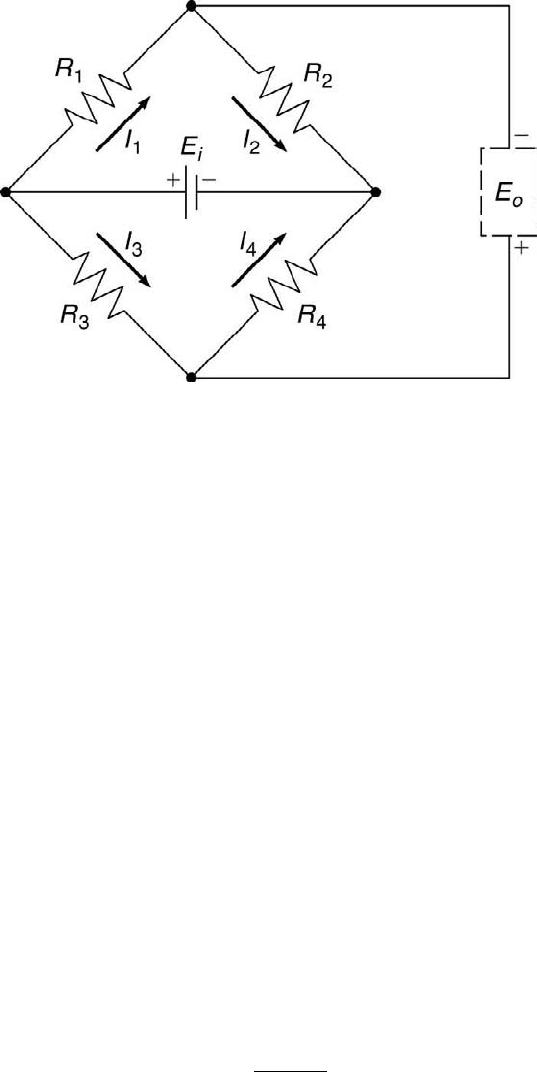
30 Measurement and Data Analysis for Engineering and Science

FIGURE 2.10

The Wheatstone bridge conﬁguration.

as pressure transducers and hot-wire anemometers. Its circuit, shown in

Figure 2.10, consists of four resistors (R

through R

), each two comprising

a pair (R

and R

; R

and R

) in series that is connected to the other pair

in parallel, and a voltage source, E

, connected between the R

-R

and the

-R

nodes. The voltage output of the bridge, E

, is measured between the

-R

and the R

-R

nodes. E

is measured by an ideal voltmeter with an

inﬁnite input impedance such that no current ﬂows through the voltmeter.

An expression needs to be developed that relates the bridge’s output

voltage to its input voltage and the four resistances. There are four un-

knowns, I

through I

. This implies that four equations are needed to reach

the desired solution. Examination of the circuit reveals that there are four

closed loops for which four equations can be written by applying Kirchhoﬀ’s

second law. The resulting four equations are

= I

+ I

, (2.20)

= I

+ I

, (2.21)

= I

− I

, (2.22)

and

= −I

+ I

. (2.23)

Kirchhoﬀ’s ﬁrst law leads to I

= I

and I

= I

, assuming no current ﬂows

through the voltmeter. These two current relations can be used in Equations

2.20 and 2.21 to give

+ R

(2.24)

Electronics 31

and

+ R

. (2.25)

These two expressions can be substituted into Equation 2.23, yielding the

desired result

= E



+ R

−

+ R



. (2.26)

Equation 2.26 leads to some interesting features of the Wheatstone

bridge. When there is no voltage output from the bridge, the bridge is

considered to be balanced even if there is an input voltage present. This

immediately yields the balanced bridge equation

. (2.27)

This condition can be exploited to use the bridge to determine an unknown

resistance, say R

, by having two other resistances ﬁxed, say R

and R

, and

varying R

until the balanced bridge condition is achieved. This is called

the null method. This method is used to determine the resistance of a

sensor which usually is located remotely from the remainder of the bridge.

An example is the hot-wire sensor of an anemometry system used in the

constant-current mode to measure local ﬂuid temperature.

FIGURE 2.11

Cantilever beam with four strain gages.

The bridge can be used also in the deﬂection method to provide an

output voltage that is proportional to a change in resistance. Assume that

resistance R

is the resistance of a sensor, such as a ﬁne wire or a strain gage.

The sensor is located remotely from the remainder of the bridge circuit in

an environment in which the temperature increases from some initial state.

Its resistance will change by an amount δR from R

to R

. Application of

Equation 2.26 yields

= E

+ R

−

+ R

. (2.28)

32 Measurement and Data Analysis for Engineering and Science

Further, if all the resistances are initially the same, where R

= R

= R, then Equation 2.28 becomes

= E



δR/R

4 + 2δR/R



= E

f(δR/R). (2.29)

Thus, when using the null and deﬂection methods, the Wheatstone bridge

can be utilized to determine a resistance or a change in resistance.

One practical use of the Wheatstone bridge is in a force measurement

system. This system is comprised of a cantilever beam, rigidly supported on

one end, that is instrumented with four strain gages, two on top and two

on bottom, as shown in Figure 2.11. The strain gage is discussed further

in Chapter 3. A typical strain gage is shown in Figure 3.3 of that chapter.

The electric conﬁguration is called a four-arm bridge. The system operates

by applying a known force, F , near the end of the beam along its centerline

and then measuring the output of the Wheatstone bridge formed by the

four strain gages. When a load is applied in the direction shown in Figure

2.11, the beam will deﬂect downward, giving rise to a tensile strain, 

, on

the top of the beam and a compressive strain, −

, on the bottom of the

beam. Because a strain gage’s resistance increases with strain, δR ∼ 

, the

resistances of the two tensile strain gages will increase and those of the two

compressive strain gages will decrease. In general, following the notation in

Figure 2.11, for the applied load condition,

= R

+ δR

, (2.30)

= R

+ δR

, (2.31)

= R

− δR

, (2.32)

and

= R

− δR

. (2.33)

If all four gages are identical, where they are of the same pattern with

= R

= R, the two tensile resistances will increase by δR

and the two compressive ones will decrease by δR. For this case, Equation

2.28 simpliﬁes to

= E

(δR/R). (2.34)

For a cantilever beam shown in Figure 2.11, the strain along the length of the

beam on its top side is proportional to the force applied at its end, F . Thus,



∼ F . If strain gages are aligned with this axis of strain, then δR ∼ 

, as

discussed in Section 3.3.2. Thus, the voltage output of this system, E

, is

linearly proportional to the applied force, F. Further, with this strain gage

conﬁguration, variational temperature and torsional eﬀects are compensated

for automatically. This is an inexpensive, simple yet elegant measurement

system that can be calibrated and used to determine unknown forces. This

Electronics 33

conﬁguration is the basis of most force balances used for aerodynamic and

mechanical force measurements.

Example Problem 2.4

Statement: Referring to Figure 2.10, if R

= 1 Ω, R

= 3 Ω, and R

= 2 Ω,

determine [a] the value of R

such that the Wheatstone bridge is balanced, and [b] the

bridge’s output voltage under this condition.

Solution: Equation 2.27 speciﬁes the relationship between resistances when the

bridge is balanced. Thus, R

= R

= (3)(2)/1 = 6 Ω. Because the bridge is bal-

anced, its output voltage is zero. This can be veriﬁed by substituting the four resistance

values into Equation 2.26.

2.6 Elementary AC Circuit Analysis

As shown in Table 2.1, the expressions for the voltages and currents of AC

circuits containing resistors, capacitors, and inductors involve diﬀerentials

and integrals with respect to time. Expressions for V (t) and I(t) of AC

circuits can be obtained directly by solving the ﬁrst-order and second-order

ordinary diﬀerential equations that govern their behavior. The diﬀerential

equation solutions for RC and RLC circuits subjected to step and sinusoidal

inputs are presented later in Chapter 4. At this point, a working knowledge

of AC circuits can be gained through some elementary considerations.

When capacitors and inductors are exposed to time-varying voltages in

AC circuits, they each create a reactance to the voltage. Reactance plus

resistance equals impedance. Symbolically, X + R = Z. Often an RLC

component is described by its impedance because it encompasses both re-

sistance and reactance. Impedance typically is considered generalized resis-

tance [2]. For DC circuit analysis, impedance is resistance because there is

no reactance. For this case, Z = R.

Voltages and currents in AC circuits usually do not vary simultaneously

in the same manner. An increase in voltage with time, for example, can be

followed by a corresponding increase in current at some later time. Such

changes of voltage and current in time are characterized best by using com-

plex number notation. This notation is described in more detail in Chapter

Assume that the voltage, V (t), and the current, I(t), are represented

by the complex numbers V

iφ

and I

iφ

, respectively. Here e

iφ

is given by

Euler’s formula,

iφ

= cos φ + i sin φ, (2.35)

where i =

√

−1. In electrical engineering texts, j is used to denote

√

−1

34 Measurement and Data Analysis for Engineering and Science

because i is used for the current. Throughout this text, i symbolizes the

imaginary number. The real voltage and real current are obtained by multi-

plying each by the complex number representation e

iωt

and then taking the

real part, Re, of the resulting number. That is,

V (t) = Re(V e

iωt

) = Re(V ) cos ωt − Im(V ) sin ωt (2.36)

and

I(t) = Re(Ie

iωt

) = Re(I) cos ωt − Im(I) sin ωt, (2.37)

in which ω is the frequency in rad/s. The frequency in cycles/s is f, where

2πf = ω.

Expressions for capacitive and inductive reactances can be derived using

the voltage and current expressions given in Equations 2.36 and 2.37 [2]. For

a capacitor, I(t) = CdV (t)/dt. Diﬀerentiating Equation 2.36 with respect

to time yields the current across the capacitor,

I(t) = −V

Cω sin ωt = Re[V

i/ωC

1/iωC

]. (2.38)

The denominator of the real component is the capacitive reactance,

= 1/iωC. (2.39)

In other words, V (t) = I(t)X

For the inductor, V (t) = LdI(t)/dt. Diﬀerentiating Equation 2.37 with

respect to time yields the voltage across the inductor,

V (t) = −I

Lω sin ωt = Re[iωLI

i/ωC

]. (2.40)

The numerator of the real component is the inductive reactance,

= i/ωL. (2.41)

Simply put, V (t) = I(t)X

Because the resistances of capacitors and inductors are eﬀectively zero,

their impedances equal the reactances. Further, the resistor has no reac-

tance, so its impedance is its resistance. Thus, Z

= R, Z

= 1/iωC, and

= iωL.

Ohm’s law is still valid for AC circuits. It now can be written as V = ZI.

Also the rules for adding resistances apply to adding impedances, where for

impedances in series

, (2.42)

and for impedances in parallel

= 1/

(

). (2.43)

Electronics 35

Example Problem 2.5

Statement: An electrical circuit loop is comprised of a resistor, R, a voltage source,

, and a 1-µF capacitor, C, that can be added into the loop by a switch. When the

switch is closed, all three electrical components are in series. When the switch is open,

the loop has only the resistor and the voltage source in series. E

= 3 V and R = 2 Ω.

Determine the expression for the current as a function of time, I(t), immediately after

the switch is closed.

Solution: Applying Kirchhoﬀ’s second law to the loop gives

RI(t) +

I(t)dt = E

This equation can be diﬀerentiated with respect to time to yield

dI(t)

I(t)

= 0,

because E

is a constant 3 V. This equation can be integrated to obtain the result

I(t) = C

−t/RC

, where C

is a constant. Now at t = 0 s, current ﬂows through the

loop and equals E

/R. This implies that C

= 3/2 = 1.5 A. Thus, for the given values

of R and C, I(t) = 1.5e

−t/(2 × 10

−6

)

. This means that the current in the loop becomes

almost zero in approximately 10 µs after the switch is closed.

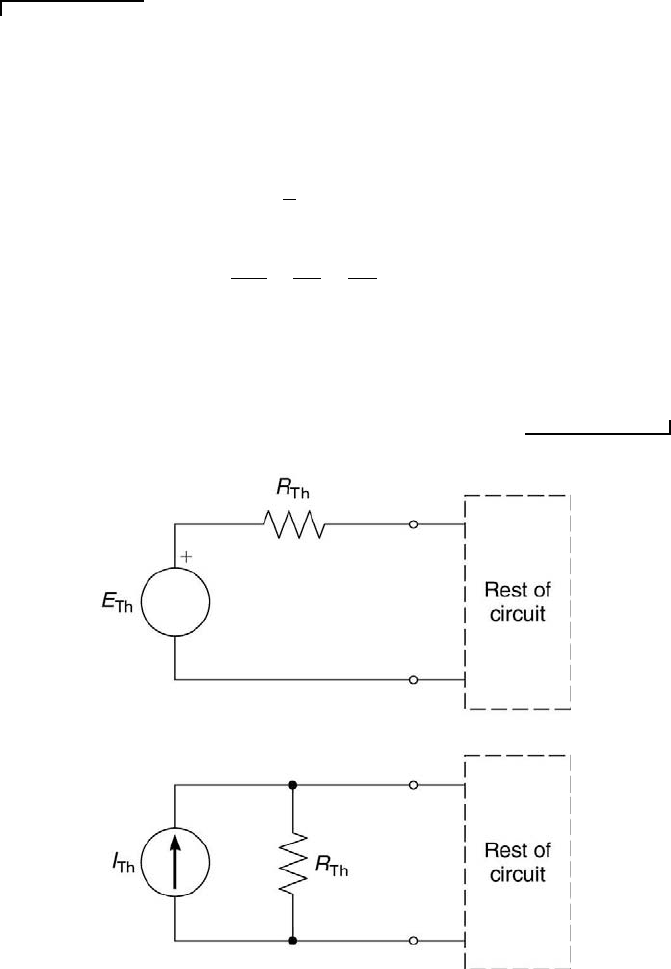
FIGURE 2.12

Th´evenin and Norton equivalent circuits.