Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition
Подождите немного. Документ загружается.


366 Measurement and Data Analysis for Engineering and Science
[y(t)]
2
=
∞
X
m=−∞
C
m
e
imω
0
t
!
∞
X
n=−∞
C
n
e
inω
0
t
!
=
∞
X
m=−∞
∞
X
n=−∞
C
m
C
n
e
i(m+n)ω
0
t
.
(9.51)
If Equation 9.51 is substituted into Equation 9.50 and the integral on the
right side is performed, the integral will equal zero unless m = −n, where,
in that case, it will equal T . This immediately leads to
[y(t)]
2
=
∞
X
n=−∞
C
n
C
−n
= 2
∞
X
n=0
A
n
2
−
iB
n
2
A
n
2
+
iB
n
2
= 2
∞
X
n=0
A
2
n
4
+
B
2
n
4
= 2
∞
X
n=0
|C
n
|
2
=
∞
X
n=−∞
|C
n
|
2
, (9.52)
where y(t) is assumed to be real and
[y(t)]
2
is termed the mean squared
amplitude or average power. Note that this equation is an approximation
to the actual mean squared amplitude whenever the number of summed
terms is finite. By comparing Equation 9.51 with the definition of the rms
for a discrete signal (see Table 9.1), it can be seen that the power is simply
the square of the rms. Recall also that the average power over a time interval
equals the product of the total energy expended over that interval and the
reciprocal of the time interval.
Equations 9.50 and 9.51 can be combined to yield Parseval’s relation for
continuous-time periodic signals
1
T
Z
T
0
[y(t)]
2
dt =
∞
X
n=−∞
|C
n
|
2
. (9.53)
This states that the total average power in a periodic signal equals the sum
of the average powers of all its harmonic components.
The n-th amplitude equals 2
q
|C
n
|
2
=
p
A
2
n
+ B
2
n
. The plot of 2
q
|C
n
|
2
versus the frequency is called the amplitude spectrum of the signal y(t).
The ordinate units are those of the amplitude. The plot of |C
n
|
2
versus the
frequency is called the power spectrum of the signal y(t). The ordinate units
are those of the amplitude squared. The absolute value squared of the C
n
Fourier coefficient, which equals one-quarter of the amplitude squared, gives
the amount of power associated with the n-th harmonic. Both spectra are
two-sided because they involve summations on both sides of n = 0. They can
be made one-sided by multiplying their values by two and then summing
from n = 0 to ∞. The power density spectrum is the derivative of the
power spectrum. Its ordinate units are those of amplitude squared divided
by frequency. So, the integral of the power density spectrum over a particular
frequency range yields the power contained in the signal in that range.
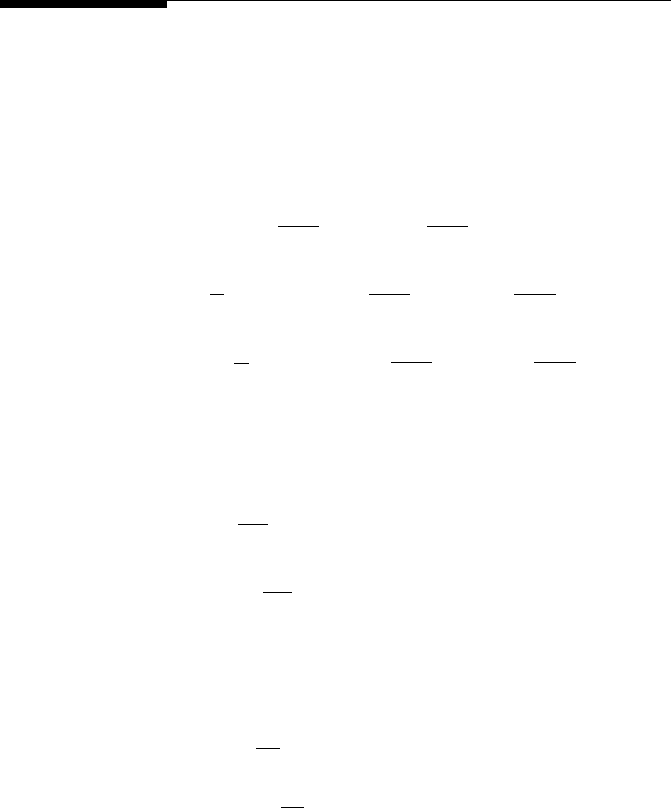
Signal Characteristics 367
The spectra of a signal obtained by impulsively tapping a cantilever beam
supported on its end, shown in Figure 9.13, displays a dominant frequency
at approximately 30 Hz.
9.9 Continuous Fourier Transform
Fourier analysis of a periodic signal can be extended to an aperiodic signal
by treating the aperiodic signal as a periodic signal with an infinite period.
From Equation 9.24, the Fourier trigonometric series representation of a
signal with zero mean (A
0
= 0) is
y(t) =
∞
X
n=1
A
n
cos
2πnt
T
+ B
n
sin
2πnt
T
=
∞
X
n=1
(
2
T
Z
T/2
−T/2
y(t) cos
2πnt
T
dt
)
cos
2πnt
T
+
∞
X
n=1
(
2
T
Z
T/2
−T/2
y(t) sin
2πnt
T
dt
)
sin
2πnt
T
. (9.54)
Noting ω
n
= 2πn/T and ∆ω = 2π/T , where ∆ω is the spacing between
adjacent harmonics, gives
y(t) =
∞
X
n=1
(
∆ω
π
Z
T/2
−T/2
y(t) cos(ω
n
t)dt
)
cos(ω
n
t)
+
∞
X
n=1
(
∆ω
π
Z
T/2
−T/2
y(t) sin(ω
n
t)dt
)
sin(ω
n
t). (9.55)
As T → ∞ and ∆ω → dω, ω
n
→ ω and the summations become integrals
with the limits ω = 0 and ω = ∞,
y(t) =
Z
∞
0
dω
π
Z
+∞
−∞
y(t) cos(ωt)dt
cos(ωt)
+
Z
∞
0
dω
π
Z
+∞
−∞
y(t) sin(ωt)dt
sin(ωt). (9.56)
Equation 9.56 can be simplified by defining
A(ω) =
Z
+∞
−∞
y(t) cos(ωt)dt (9.57)

368 Measurement and Data Analysis for Engineering and Science
and
B(ω) =
Z
+∞
−∞
y(t) sin(ωt)dt. (9.58)
A(ω) and B(ω) are the components of the Fourier transform of y(t). Note
that A(ω) and B(ω) have units of y/ω, whereas A
n
and B
n
in Equations
9.26 and 9.27, respectively, have units of y. A(ω) is an even function of ω and
B(ω) is an odd function of ω. Substituting these definitions into Equation
9.56 yields
y(t) =
1
π
Z
∞
0
A(ω) cos(ωt)dω +
1
π
Z
∞
0
B(ω) sin(ωt)dω
=
1
2π
Z
∞
−∞
A(ω) cos(ωt)dω +
1
2π
Z
∞
−∞
B(ω) sin(ωt)dω. (9.59)
Note that these integrals involve negative frequencies. The negative fre-
quencies are simply a consequence of the mathematics and have no mystical
significance.
The complex Fourier coefficient is defined as
Y (ω) ≡ A(ω) − iB(ω). (9.60)
Substituting the definitions of the Fourier coefficients gives
Y (ω) =
Z
+∞
−∞
y(t)[cos(ωt) − i sin(ωt)]dt =
Z
+∞
−∞
y(t)e
−iωt
dt. (9.61)
This equation expresses that Y (ω) is the Fourier transform of y(t). |Y (ω)|
2
corresponds to the amount of power contained in the frequency range from
ω to ω + dω.
The inverse Fourier transform of Y (ω) can be developed. Note that
i
2π
Z
+∞
−∞
A(ω) sin(ωt)dω = 0, (9.62)
because A(ω) and sin(ωt) are orthogonal. Likewise,
−i
2π
Z
+∞
−∞
B(ω) cos(ωt)dω = 0, (9.63)
because B(ω) and cos(ωt) are orthogonal. These integral terms can be added
to those in Equation 9.59, which results in
Signal Characteristics 369
y(t) =
1
2π
Z
∞
−∞
A(ω) cos(ωt)dω +
1
2π
Z
∞
−∞
B(ω) sin(ωt)dω
+
i
2π
Z
∞
−∞
A(ω) sin(ωt)dω −
i
2π
Z
∞
−∞
B(ω) cos(ωt)dω
=
1
2π
Z
∞
−∞
[A(ω) − iB(ω)][cos(ωt) + i sin(ωt)]dω
=
1
2π
Z
∞
−∞
Y (ω)e
iωt
dω. (9.64)
Equations 9.61 and 9.64 form the Fourier transform pair, which con-
sists of the Fourier transform of y(t),
Y (ω) =
Z
∞
−∞
y(t)e
−iωt
dt, (9.65)
and the inverse Fourier transform of Y (ω),
y(t) =
1
2π
Z
∞
−∞
Y (ω)e
iωt
dω. (9.66)
Equation 9.65 determines the amplitude-frequency characteristics of the sig-
nal y(t) from its amplitude-time characteristics. Equation 9.66 constructs
the amplitude-time characteristics of the signal from its amplitude-frequency
characteristics. Taking the inverse Fourier transform of the Fourier trans-
form always should recover the original y(t).
9.10 *Continuous Fourier Transform Properties
Many useful properties can be derived from the Fourier transform pair [3].
These properties are relevant to understanding how signals in the time do-
main are represented in the frequency domain. Examine the Fourier trans-
form
Y (ω) = 2πδ(ω − ω
o
), (9.67)
where δ(x) denotes the delta function, which has the properties
R
∞
−∞
δ(0) = 1
and
R
∞
−∞
δ(6= 0) = 0. Substitution of this expression into Equation 9.66
yields
y(t) =
1
2π
Z
∞
−∞
2πδ(ω − ω
o
)e
iωt
dω = e
iω
o
t
. (9.68)
Thus, the Fourier transform of y(t) = e
iω
o
t
is 2πδ(ω − ω
o
). This transform
occurs in those involving sine and cosine functions, which are the foundations
of the Fourier series.
370 Measurement and Data Analysis for Engineering and Science
y(t)
Y (ω)
Property
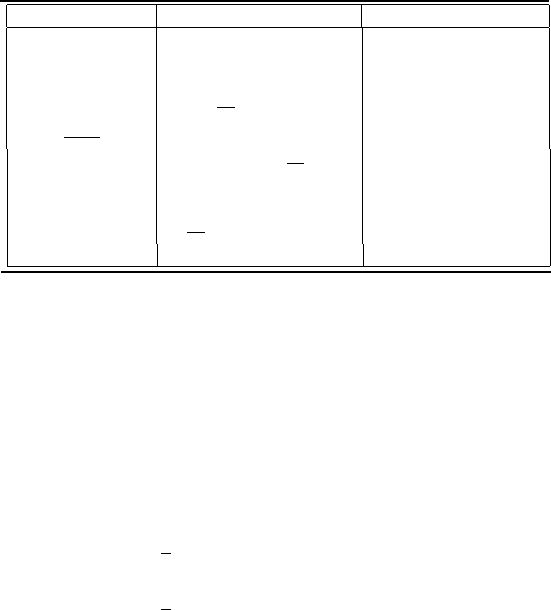
ax
1
(t) + bx
2
(t)
aX
1
(ω) + bX
2
(ω)
linearity
x(t − t
o
)
X(ω)e
−iωt
o
time shifting
x(t)e
iω
o
t
X(ω − ω
o
)
frequency shifting
x(at)
1
|a|
X(ω/a)
time scaling
dx(t)
dt
iωX(ω)
time differentiation
R
t
−∞
x(τ)dτ
πX(0)δ(ω) +
1
iω
X(ω)
integration
x
e
(t)
Re[X(ω)] = a(ω)
even signal
x
o
(t)
iIm[X(ω)] = iB(ω)
odd signal
x
1
(t)x
2
(t)
1
2π
X
1
(ω) ∗ X
2
(ω)
multiplication
x
1
(t) ∗ x
2
(t)
X
1
(ω) + X
2
(ω)
convolution
TABLE 9.2
Properties of the continuous Fourier transform.
As an example, consider the Fourier transform of y(t) = cos(ω
o
t) and,
consequently, how that signal is represented in the frequency domain. Sub-
stituting the complex expression for the cosine function (Equation 9.35) into
Equation 9.65 gives
Y (ω) =
1
2
Z
∞
−∞
[e
iω
o
t
+ e
−iω
o
t
]e
−iωt
dt
=
1
2
Z
∞
−∞
[e
iω
o
t
e
−iωt
+ e
−iω
o
t
e
−iωt
]dt
= π[δ(ω − ω
o
) + δ(ω + ω
o
)], (9.69)
using Equations 9.67 and 9.68. This implies that the signal y(t) = cos(ω
o
t)
in the time domain appears as impulses of amplitude π in the frequency
domain at ω = −ω
o
and ω = ω
o
.
In a similar manner, the Fourier transform of y(t) = x(t)e
iω
o
t
becomes
Y (ω) =
Z
∞
−∞
x(t)e
iω
o
t
e
−iωt
dt
=
Z
∞
−∞
e
−i(ω−ω
o
)t
dt
= X(ω − ω
o
). (9.70)
The multiplication of the signal x(t) by e
iω
o
t
is called complex modula-
tion. Equation 9.70 implies that the Fourier transform of x(t)e
iω
o
t
results
in a frequency shift, from ω to ω − ω
o
, in the frequency domain.
The multiplication of two functions in one domain is related to the con-
volution the two functions’ transforms in the transformed domain. The con-
Signal Characteristics 371
volution of the functions x
1
(t) and x
2
(t) is
x
1
(t) ∗ x
2
(t) =
Z
t
0
x
1
(τ)x
2
(t − τ )dτ, (9.71)
in which the ∗ denotes the convolution operator. This leads immediately to
the multiplication and convolution properties of the Fourier transform that
are presented in Table 9.2. These two properties are quite useful because
one function often can be expressed as the product of two functions whose
Fourier transforms or inverse transforms are known.
Example Problem 9.6
Statement: Determine 3 ∗ sin 2ω.
Solution: Let X
1
(ω) = 3 and X
2
(ω) = sin 2ω. Thus, X
1
(τ) = 3 and X
2
(ω − τ ) =
sin 2(ω − τ ). Applying Equation 9.71 gives
3 ∗ sin 2ω =
Z
ω
0
3 sin 2(ω − τ )dτ =
3
2
cos 2(ω − τ )|
ω
0
=
3
2
[1 − cos 2ω] .
372 Measurement and Data Analysis for Engineering and Science
9.11 Problem Topic Summary
Topic
Review Problems
Homework Problems
Signal Characteristics
5, 6, 7, 8, 9, 11, 12
3, 7, 13, 15
Signal Parameters
1, 2, 10
1, 2, 3, 4, 7, 9, 10, 14
Fourier Series
3, 4
5, 6, 7, 8, 11, 12, 14
TABLE 9.3
Chapter 9 Problem Summary
9.12 Review Problems
1. Consider the deterministic signal y(t) = 3.8 sin(ωt), where ω is the cir-
cular frequency. Determine the rms value of the signal to three decimal
places.
2. Compute the rms of the dimensionless data set in the file data10.dat.
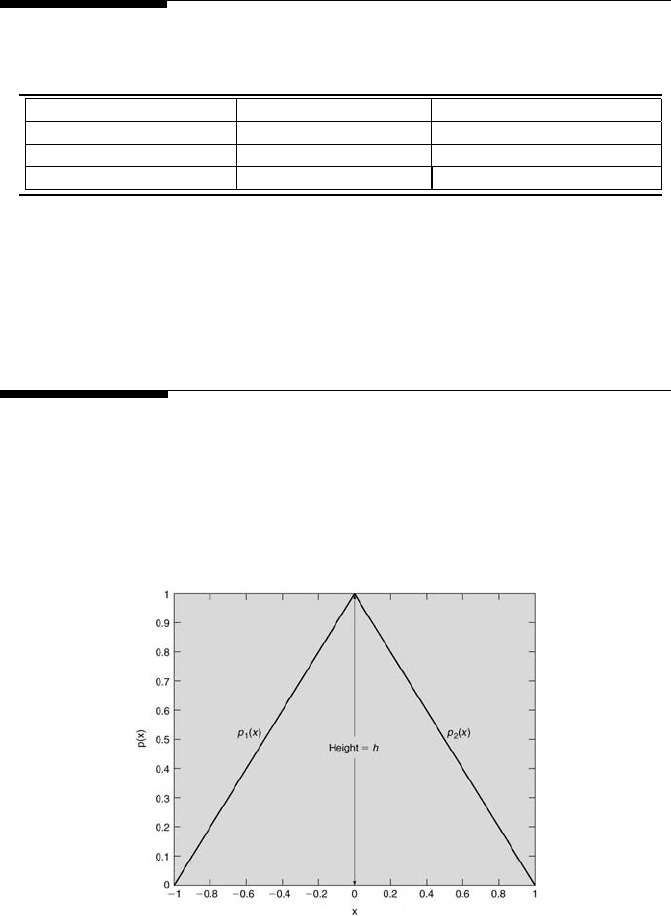
FIGURE 9.14
Triangular function.

Signal Characteristics 373
FIGURE 9.15
Rectangular function.
3. Find the third Fourier coefficient of the function pictured in Figure 9.14,
where h = 1. (Note: Use n = 3 to find the desired coefficient.) Consider
the function to be periodic. Respond to three significant figures.
4. What is the value of the power spectrum at the cyclic frequency 1 Hz
for the function given by the Figure 9.15? Respond to three significant
figures. (The desired result is achieved by representing the function on
an infinite interval.)
5. Which one of the following functions is periodic? (a) x(t) = 5 sin(2πt)
or (b) x(t) = cos(2πt) exp(−5t).
6. Which one of the following is true? A stationary random process must
(a) be continuous, (b) be discrete, (c) be ergodic, (d) have ensemble aver-
aged properties that are independent of time, or (e) have time averaged
properties that are equal to the ensemble averaged properties.
7. Which of the following are true? An ergodic random process must (a) be
discrete, (b) be continuous, (c) be stationary, (d) have ensemble aver-
aged properties that are independent of time, or (e) have time averaged
properties that are equal to the ensemble averaged properties.
8. Which of the following are true? A single time history record can be
used to find all the statistical properties of a process if the process is (a)
deterministic, (b) ergodic, (c) stationary, or (d) all of the above.
9. Which of the following are true? The autocorrelation function of a sta-
tionary random process (a) must decrease as |τ| increases, (b) is a func-
tion of |τ| only, (c) must approach a constant as |τ| increases, or (d)
must always be non-negative.

374 Measurement and Data Analysis for Engineering and Science
10. Determine for the time period from 0 to 2T the rms value of a square
wave of period T given by y(t) = 0 from 0 to T /2 and y(t) = A from
T /2 to T .
11. Which of the following functions are periodic? (a) y (t) = 5 sin (5t) +
3 cos (5t), (b) y (t) = 5 sin (5t) e
t+2
12
, (c) y (t) = 5 sin (5t) + e
t+2
12
, (d)
y (t) = 15 sin (5t) cos (5t).
12. A speed of a turbine shaft is 13 000 revolutions per minute. What are its
cyclic frequency (in Hz), period (in s), and circular frequency (in rad/s)?
9.13 Homework Problems
1. Determine the autocorrelation of x(t) for (a) x(t) = c, where c is a
constant, (b) x(t) = sin(2πt), and (c) x(t) = cos(2πt).
2. Determine the average and rms values for the function y(t) = 30 +
2 cos(6πt) over the following time periods: (a) 0 s to 0.1 s, (b) 0.4 s to
0.5 s, (c) 0 s to
1
3
s, and (d) 0 s to 20 s.
3. Consider the deterministic signal y(t) = 7 sin(4t) with t in units of sec-
onds and 7 (the signal’s amplitude) in units of volts. Determine the
signal’s (a) cyclic frequency, (b) circular frequency, (c) period for one
cycle, (d) mean value, and (e) rms value. Put the correct units with
each answer. Below are two integrals that may or may not be needed:
Z
sin
2
(x)dx =
1
2
x −
1
4
sin(2x)
and
Z
cos
2
(x)dx =
1
2
x +
1
4
sin(2x).
4. For the continuous periodic function y(t) = y
1
(t) −y
2
(t), where y
1
(t) =
A(t/T )
1/2
and y
2
(t) = B(t/T ), determine for one period (a) the mean
value of y(t) and (b) the rms of y
1
(t).
5. Determine the Fourier series for the period T of the function described
by
y(t) =
4At
T
+ A for −
T
2
≤ t ≤ 0
and
y(t) =
−4At
T
+ A for 0 ≤ t ≤
T
2
.

Signal Characteristics 375
Do this without using any computer programs or spreadsheets. Show all
work. Then, on one graph, plot the three resulting series for 2, 10, and
50 terms along with the original function y(t).
6. Determine the Fourier series of the function
y(t) = t for − 5 < t < 5.
(This function repeats itself every 10 units, such as from 5 to 15, 15 to
25, ...). Do this without using any computer programs or spreadsheets.
Show all work. Then, on one graph, plot the three resulting series for 1,
2, and 3 terms along with the original function y(t).
7. Consider the signal y(t) = 2 + 4 sin(3πt) + 3 cos(3πt) with t in units of
seconds. Determine (a) the fundamental frequency (in Hz) contained in
the signal and (b) the mean value of y(t) over the time period from 0 s
to 2/3 s. Also (c) sketch the amplitude-frequency spectrum of y(t).
8. For the Fourier series
y(t) = (20/π)[sin(4πt/7) + 4 sin(8πt/7) + 3 sin(12πt/7) + 5 sin(16πt/7)],
determine the amplitude of the third harmonic.
9. Calculate the mean value of a rectified sine wave given by
y = |A sin
2πt
T
|
during the time period 0 < t < 1000T .
10. Determine the rms (in V) of the signal y(t) = 7 sin(4t) where y is in
units of V and t is in units of s. An integral that may be helpful is
R
sin
2
axdx = x/2 − (1/4a) sin(2ax).
11. Determine the Fourier coefficients A
0
, A
n
, and B
n
, and the trigonometric
Fourier series for the function y(t) = At, where the function has a period
of 2 s with y(−1) = −A and y(1) = A.
12. Consider the following combination of sinusoidal inputs:
y (t) = sin (t) + 2 cos (2t) + 3 sin (2t) + cos (t) .
(a) Rewrite this equation in terms of only cosine functions. (b) Rewrite
this equation in terms of only sine functions. (c) What is the fundamental
period of this combination of inputs?
