Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

336 Measurement and Data Analysis for Engineering and Science

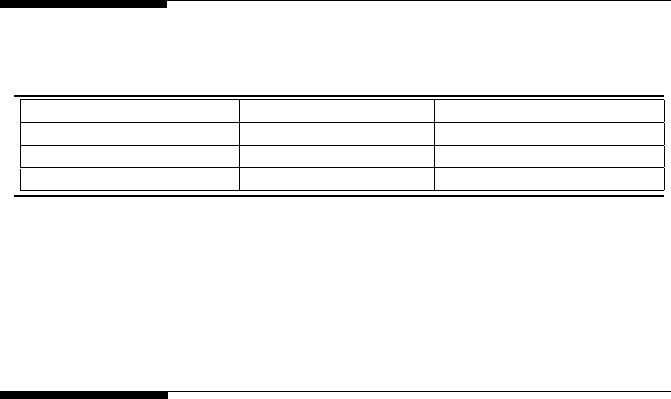
8.13 Problem Topic Summary

Topic

Review Problems

Homework Problems

Regression Analysis

1, 2, 3, 4, 7, 8

1, 2, 3, 6, 8, 11, 12

Linearly Intrinsic

4, 5, 7, 9, 10

Regression Parameters

4, 5, 6

TABLE 8.3

Chapter 8 Problem Summary

8.14 Review Problems

1. Consider the following set of three (x, y) data pairs: (0, 0), (3, 2), and

(6, 7). Determine the intercept of the best-ﬁt line for the data to two

decimal places.

2. Consider the following set of three (x, y) data pairs: (0, 0),(3, 0) and (9,

5). Determine the slope of the best-ﬁt line for the data to two decimal

places.

3. Who is the famous mathematician who developed the method of least

squares?

4. Consider the following set of three (x, y) data pairs: (1.0, 1.7), (2.0,

4.3), and (3.0, 5.7). A linear least-squares regression analysis yields the

best-ﬁt equation y = −0.10 + 2.00x. Determine the standard error of

the ﬁt rounded oﬀ to two decimal places.

5. Consider the following set of three (x, y) data pairs: (1.0, 1.7), (2.0,

4.3), and (3.0, 5.7). A linear least-squares regression analysis yields the

best-ﬁt equation y = −0.10 + 2.00x. Determine the precision interval

based upon 95 % conﬁdence rounded oﬀ to two decimal places. Assume

a value of 2 for the Student-t factor.

6. An experimenter determines the precision interval, PI-1, for a set of data

by performing a linear least-squares regression analysis. This interval is

based upon three measurements and 50 % conﬁdence. Then the same

experiment is repeated under identical conditions and a new precision

interval, PI-2, is determined based upon 15 measurements and 95 %

Regression and Correlation 337

conﬁdence. The ratio of PI-2 to PI-1 is (a) less than one, (b) greater

than one, (c) equal to one, or (d) could be any of the above.

7. A strain gage-instrumented beam was calibrated by hanging weights

of 1.0 N, 2.0 N, and 3.0 N at the end of the beam and measuring the

corresponding output voltages. A linear least-squares regression analysis

of the data yielded a best-ﬁt intercept equal to 1.00 V and a best-ﬁt slope

equal to 2.75 V/N. At 1.0 N, the recorded voltage was 3.6 V and at 2.0

N it was 6.8 V. What was the recorded voltage at 3.0 N?

8. A linear least-squares regression analysis ﬁt of the (x, y) pairs (0, 1), (1,

3.5), (2, 5.5), (3, 7), and (4, 9.5) must pass through (a) (0, 1), (b) (1,

3.5), (c) (2, 5.3), (d) (3, 8), or (e) (4, 9.5)? Why (give one reason)?

8.15 Homework Problems

1. Prove that a least-squares linear regression analysis ﬁt always goes

through the point (¯x,¯y).

2. Starting with the equation y

− ¯y = (y

− y

) + (y

− ¯y) and using

the normal equations, prove that

i=1

−

i=1

− y

)

i=1

−

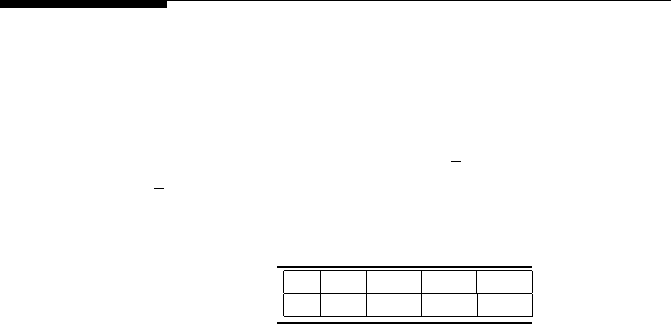
3. Find the linear equation that best ﬁts the data shown in Table 8.4.

5.1

10.5

14.7

20.3

TABLE 8.4

Calibration data.

4. Determine the best-ﬁt values of the coeﬃcients a and b in the expression

y = 1 / (a + bx) for the (x, y) data pairs (1.00, −1.11), (2.00, −0.91),

(3.00, −0.34), (4.00, −0.20), and (5.00, −0.14).

5. For an ideal gas, pV

= C. Using regression analysis, determine the

best-ﬁt value for γ given the data shown in Table 8.5.

6. The data presented in Table 8.6 was obtained during the calibration of a

cantilever-beam force-measurement system. The beam is instrumented

with four strain gages that serve as the legs of a Wheatstone bridge. In

the table F (N) denotes the applied force, E(V) the measured output

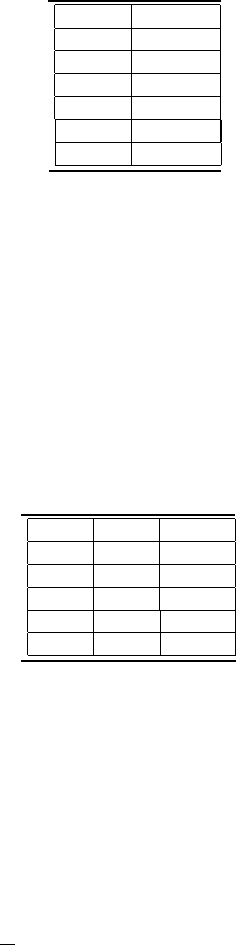
338 Measurement and Data Analysis for Engineering and Science

p (psi)

V (in.

)

16.6

39.7

78.5

115.5

195.3

546.1

TABLE 8.5

Gas pressure-volume data.

voltage, and u

(V) the measurement uncertainty in E. Based upon a

knowledge of how such a system operates, what order of the ﬁt would

model the physics of the system most appropriately? Perform a regres-

sion analysis of the data for various orders of the ﬁt. What is the order of

the ﬁt that has the lowest value of S

? What is the order of the ﬁt that

has the smallest precision interval, ±t

ν,P

, that is required to have

the actual ﬁt curve agree with all of the data to within the uncertainty

of E?

F (N)

E(V)

(V)

0.4

2.7

0.1

1.1

3.6

0.2

1.9

4.4

0.2

3.0

5.2

0.3

5.0

9.2

0.5

TABLE 8.6

Strain-gage force-balance calibration data with uncertainty.

7. A hot-wire anemometry system probe inserted into a wind tunnel is

used to measure the tunnel’s centerline velocity, U. The output of the

system is a voltage, E. During a calibration of this probe, the data

listed in Table 8.7 was acquired. Assume that the uncertainty in the

voltage measurement is 2 % of the indicated value. Using a linear least-

squares regression analysis determine the best ﬁt values of A and B in

the relation E

= A + B

√

U. Finally, plot the ﬁt with 95 % conﬁdence

intervals and the data with error bars as voltage versus velocity. Is the

assumed relation appropriate?

Regression and Correlation 339

Velocity (m/s)

Voltage (V)

0.00

3.19

3.05

3.99

6.10

4.30

9.14

4.48

12.20

4.65

TABLE 8.7

Hot-wire probe calibration data.

8. The April 3, 2000 issue of Time Magazine published the body mass

index (BMI) of each Miss America from 1922 to 1999. The BMI is de-

ﬁned as “the weight divided by the square of the height”. (Note: The

units of the BMI are speciﬁed as kg/m

, which strictly is mass divided

by the square of the height.) The author argues, based on the data,

that Miss America may dwindle away to nothing if the BMI-versus-year

progression continues. Perform a linear least-squares regression analysis

on the data and determine the linear regression coeﬃcient. How statis-

tically justiﬁed is the author’s claim? Also determine how many Miss

Americas have BMIs that are below the World Health Organization’s

cutoﬀ for undernutrition, which is a BMI equal to 18.6. Use the data ﬁle

missamer.dat that contains two columns, the year and the BMI.

9. For the ideal gas data presented in Table 8.5, determine the standard

error of the ﬁt, S

, for the best ﬁt found using linear regression analysis.

Plot the best-ﬁt relation of p as a function of V along with the data and

the precision intervals of 90 % and 99 % conﬁdence, all on the same

graph.

10. Given the (x, y) data pairs (0, 0.2), (1, 1.3), (2, 4.8), and (3, 10.7), (a)

develop the expressions (but do not solve them) for variables x and y

such that a least-squares linear-regression analysis could be used to ﬁt

the data to the non-linear expression y = axe

+ b, where a and b are

best-ﬁt constants. Then, (b) determine the value of b.

11. The four (x, y) data pairs (2, 2), (4, 3), (6, 5), and (8, 6) are ﬁtted using

the method of linear least-squares regression. Determine the calculated

y value through which the ﬁt passes when x = 5 without doing the

regression analysis.

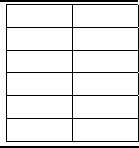
12. The data presented in the Table 8.8 was obtained during a strain-gage

force balance calibration, where F (N) denotes the applied force in N and

E(V) the measured output voltage in V. Determine a suitable least-

squares ﬁt of the data using the appropriate functions in MATLAB.

Quantify the best ﬁt through the standard error of the ﬁt, S

. Which

340 Measurement and Data Analysis for Engineering and Science

F (N)

E(V)

0.4

2.7

1.1

3.6

1.9

4.4

3.0

5.2

5.0

9.2

TABLE 8.8

Strain-gage force-balance calibration data.

polynomial ﬁt has the lowest value of S

? Which polynomial ﬁt is the

most suitable (realistic) based on your knowledge of strain-gage system

calibrations? Plot each polynomial ﬁt on a separate graph and include

error bars for the y-variable, with the magnitude of error bar estimated

at 95 % conﬁdence and based on S

. Use the M-ﬁle plotfit.m. This

M-ﬁle requires three columns of data, where the third column is the

measurement uncertainty in y. Table 8.8 does not give those, so they

must be added. Assume that each y measurement uncertainty is 5 %

of the measured E(V) value. S

is actually the curve-ﬁt uncertainty.

plotfit.m shows this uncertainty as dotted lines (not as error bars as in

the problem statement). The M-ﬁle plotfit.m also prints out the S

value and calculates the precision interval (±t

ν,P

) to help plot the

dotted lines. Calculate the y measurement uncertainties and use them

as a third column input to the M-ﬁle, then run plotfit.m for each order

of the curve ﬁt desired. Also be sure to label the axes appropriately.

Bibliography

[1] S.M. Stigler. 1986. The History of Statistics. Cambridge: Harvard Uni-

versity Press.

[2] K. Alder. 2002. The Measure of All Things. London: Little, Brown.

[3] Bevington, P.R. and D.K. Robinson. 1992. Data Reduction and Error

Analysis for the Physical Sciences. New York: McGraw-Hill.

[4] J.R. Taylor. 1982. An Introduction to Error Analysis. Mill Valley: Uni-

versity Science Books.

[5] W.A. Rosenkrantz. 1997. Introduction to Probability and Statistics for

Scientists and Engineers. New York: McGraw-Hill.

[6] Montgomery, D.C., and G.C. Runger. 1994. Applied Statistics and Prob-

ability for Engineers. New York: John Wiley and Sons.

[7] Miller, I. and J.E. Freund. 1985. Probability and Statistics for Engineers.

3rd ed. Englewood Cliﬀs: Prentice Hall.

[8] D.J. Finney. 1952. Probability Analysis. Cambridge: Cambridge Univer-

sity Press.

[9] W.E. Deming. 1943. Statistical Adjustment of Data. New York: John Wi-

ley and Sons.

[10] J. Mandel. 1984. The Statistical Analysis of Experimental Data. New

York: Dover.

[11] S. Nakamura. 1996. Numerical Analysis and Graphic Visualization with

MATLAB. Englewood Cliﬀs: Prentice Hall.

[12] Press, W.H., Teukolsky, S.A., Vetterling, W.T., and B.P. Flannery. 1992.

Numerical Recipes, 2nd ed. Cambridge: Cambridge University Press.

[13] W.J. Palm, III. 1999. MATLAB for Engineering Applications. New York:

McGraw-Hill.

[14] F. Galton. 1892. Hereditary Genius: An Inquiry into its Laws and Con-

sequences. 2nd ed. London: Macmillan.

[15] Coleman, H., and W.G. Steele. 1999. Experimentation and Uncertainty

Analysis for Engineers. 2nd ed. New York: Wiley Interscience.

341

342 Measurement and Data Analysis for Engineering and Science

[16] F. Galton. 1888. Co-relations and their Measurement, Chieﬂy from An-

thropometric Data. Proceedings of the Royal Society of London 45: 135-

145.

Signal Characteristics

CONTENTS

9.1 Chapter Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 343

9.2 Signal Characterization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 344

9.3 Signal Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 347

9.4 Signal Statistical Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 349

9.5 Fourier Series of a Periodic Signal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354

9.6 Complex Numbers and Waves . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 361

9.7 Exponential Fourier Series . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363

9.8 Spectral Representations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 365

9.9 Continuous Fourier Transform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 367

9.10 *Continuous Fourier Transform Properties . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 369

9.11 Problem Topic Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 372

9.12 Review Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 372

9.13 Homework Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 374

... there is a tendency in all observations, scientiﬁc and otherwise, to see

what one is looking for ...

D.J. Bennett. 1998. Randomness. Cambridge: Harvard University Press.

But you perceive, my boy, that it is not so, and that facts, as usual, are very

stubborn things, overruling all theories.

Professor VonHardwigg in Voyage au centre de la terra by Jules Gabriel Verne,

1864.

9.1 Chapter Overview

One of the key requirements in performing a successful experiment is a

knowledge of signal characteristics. Signals contain vital information about

the process under investigation. Much information can be extracted from

them, provided the experimenter is aware of the methods that can be used

and their limitations. In this chapter, the types of signals and their charac-

teristics are identiﬁed. Formulations of the statistical parameters of signals

are presented. Fourier analysis and synthesis are introduced and used to

ﬁnd the amplitude, frequency, and power content of signals. These tools are

343

344 Measurement and Data Analysis for Engineering and Science

applied to continuous signals, ﬁrst to some classic periodic signals and then

to aperiodic signals. In the following chapter, these methods are extended

to digital signal analysis.

9.2 Signal Characterization

In the context of measurements, a signal is a measurement system’s repre-

sentation of a physical variable that is sensed by the system. More broadly,

it is deﬁned as a detectable, physical quantity or impulse (as a voltage, cur-

rent, or magnetic ﬁeld strength) by which messages and information can be

transmitted [1]. The information contained in a signal is related to its size

and extent. The size is characterized by the amplitude (magnitude) and

the extent (timewise or samplewise variation) by the frequency. The ac-

tual shape of a signal is called its waveform. A plot of a signal’s amplitude

versus time is called a time history record. A collection of N time history

records is called an ensemble, as illustrated in Figure 9.1. An ensemble also

can refer to a set of many measurements made of a single entity, such as the

weight of an object determined by each student in a science class, and of

many entities of the same kind made at the same time, such as everyone’s

weight on New Year’s morning.

Signals can be classiﬁed as either deterministic or nondeterministic

(random). A deterministic signal can be described by an explicit math-

ematical relation. Its future behavior, therefore, is predictable. Each time

history record of a random signal is unique. Its future behavior cannot be

determined exactly but to within some limits with a certain conﬁdence.

Deterministic signals can be classiﬁed into static and dynamic signals,

which are subdivided further, as shown in Figure 9.2. Static signals are

steady in time. Their amplitude remains constant. Dynamic signals are ei-

ther periodic or aperiodic. A periodic signal, y(t), repeats itself at regular

intervals, nT , where n = 1, 2, 3, .... Analytically, this is expressed as

y(t + T ) = y(t) (9.1)

for all t. The smallest value of T for which Equation 9.1 holds true is called

the fundamental period. If signals y(t) and z(t) are periodic, then their

product y(t)z(t) and the sum of any linear combination of them, c

y(t) +

z(t), are periodic.

A simple periodic signal has one period. A complex periodic signal has

more than one period. An almost-periodic signal is comprised of two or

more sinusoids of arbitrary frequencies. However, if the ratios of all possible

pairs of frequencies are rational numbers, then an almost-periodic signal is

periodic.

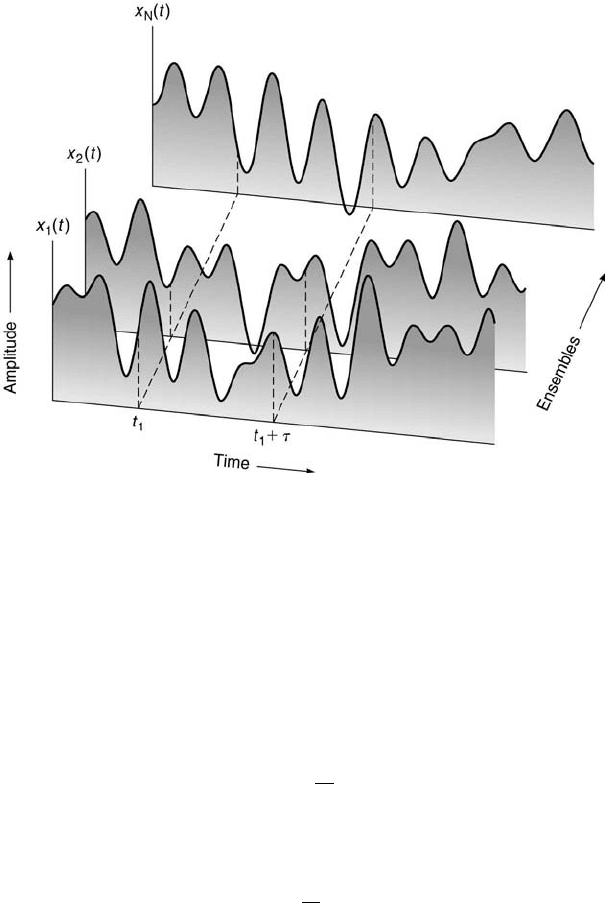
Signal Characteristics 345

FIGURE 9.1

An ensemble of N time history records.

Nondeterministic signals are classiﬁed as shown in Figure 9.3. Proper-

ties of the ensemble of the nondeterministic signals shown in Figure 9.1 can

be computed by taking the average of the instantaneous property values

acquired from each of the time histories at an arbitrary time, t

. The en-

semble mean value, µ

), and the ensemble autocorrelation function (see

Chapter 8 for more on the autocorrelation), R

, t

+ τ), are

) = lim

N→∞

i=1

) (9.2)

and

, t

+ τ) = lim

N→∞

i=1

+ τ), (9.3)

in which τ denotes an arbitrary time measured from time t

. Both equations

represent ensemble averages. This is because µ

) and R

, t

+τ) are

determined by performing averages over the ensemble at time t

If the values of µ

) and R

, t

+ τ ) change with t

, then the sig-

nal is nonstationary. Otherwise, it is stationary (stationary in the wide

sense). A nondeterministic signal is considered to be weakly stationary