Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

396 Measurement and Data Analysis for Engineering and Science

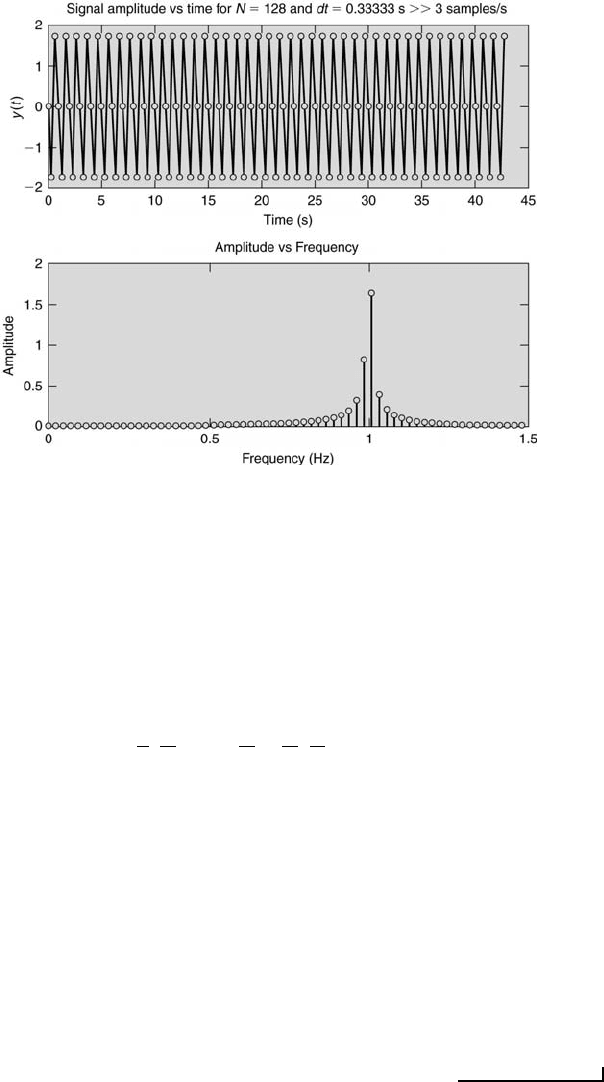
FIGURE 10.14

Signal and frequency spectrum with dt = 1/3 s.

of T

and T

is sought. Recalling that T = Nδt = N/f

, if m/2 = N/f

no amplitude

ambiguity will be present. That is, when N = f

(m/2) = (5/2)m, with m and N

integers, there will be no amplitude ambiguity. This occurs, for example, when m = 2

(with N = 5) and m = 4 (with N = 10). However, all the frequencies of interest should

be seen in the spectrum. The highest frequency of interest is f

max

= f

/2.

Because there are N/2 discrete frequencies and assuming that f

min

= 0 needs to be

considered, this yields

max

(

− 1) =

(

− 1) (T = N/f

Solving for N,

N = 2f

/(f

− 4).

So, when f

= 5, N = 10/(5 −4). Thus, N = 10 is the minimum N needed to see both

components.

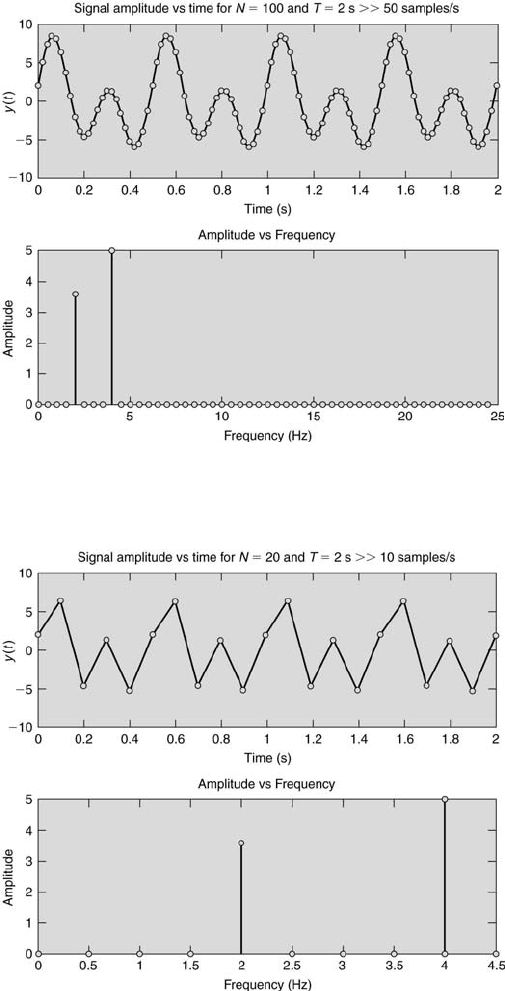
For case (i), the discrete signal and the amplitude-frequency spectrum are correct.

This is shown in Figure 10.15.

For case (ii), the spectrum remains correct and the discrete signal, although still

correct, does not represent the signal well because of the lower sampling rate. This is

illustrated in Figure 10.16.

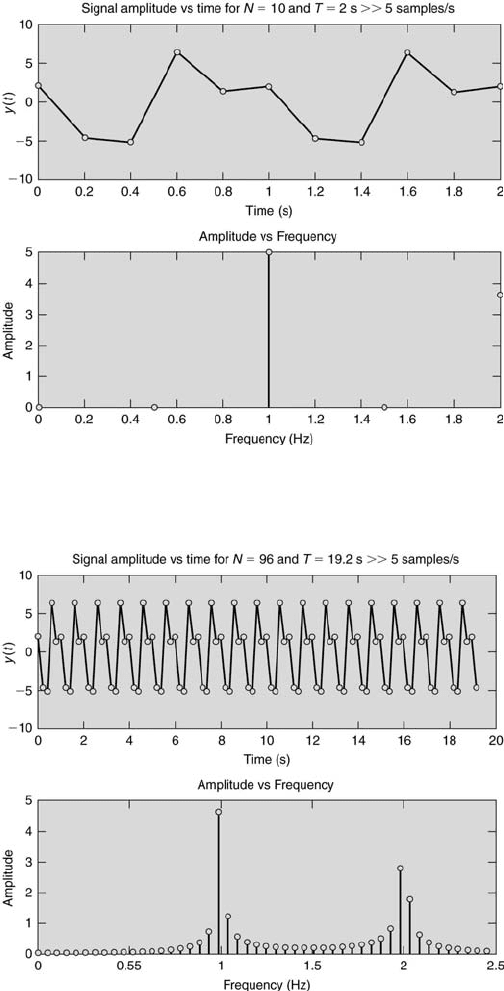
For case (iii), the 4 Hz component is aliased down to 1 Hz and the 2 Hz component

is correct. No amplitude ambiguity has occurred. This is displayed in Figure 10.17.

For case (iv), amplitude ambiguity has occurred for both components and only the

4 Hz component is aliased down to 1 Hz. This is shown in Figure 10.18.

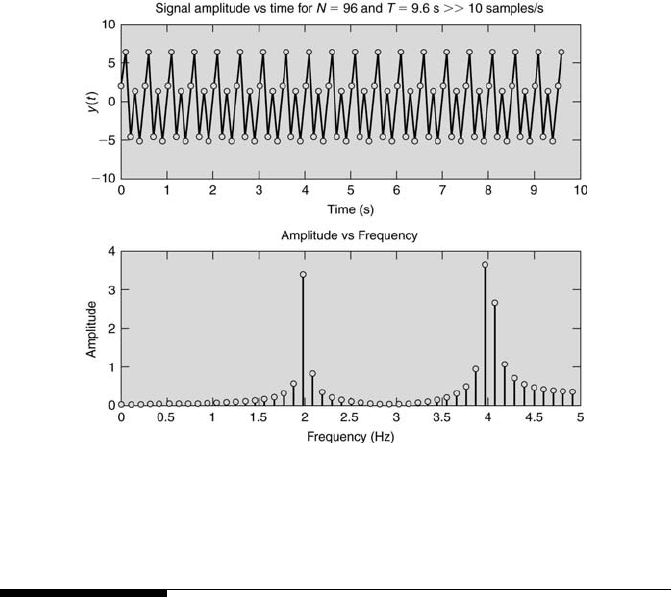
For case (v), amplitude ambiguity has occurred but not aliasing. This is presented

in Figure 10.19.

Signal Analysis 397

FIGURE 10.15

Signal and frequency spectrum with N = 100, f

= 50.

FIGURE 10.16

Signal and frequency spectrum with N = 20, f

= 10.

398 Measurement and Data Analysis for Engineering and Science

FIGURE 10.17

Signal and frequency spectrum with N = 10, f

= 5.

FIGURE 10.18

Signal and frequency spectrum with N = 96, f

= 5.

Signal Analysis 399

FIGURE 10.19

Signal and frequency spectrum with N = 96, f

= 10.

10.7 *Windowing

Because either an aperiodic or random signal does not have a period, the

Fourier transform applied to such a signal’s ﬁnite record length produces

leakage in its spectrum. This eﬀect can be minimized by applying a win-

dowing function. This process eﬀectively attenuates the signal’s ampli-

tude near the discontinuities that were discussed previously in Section 10.6,

thereby leading to less leakage. The windowing function actually is a func-

tion that weights the signal’s amplitude in time. The eﬀect of a windowing

function on the spectrum can be seen by examining the convolution of two

Fourier transforms, one of the signal and the other of the windowing func-

tion. This is considered next.

The discrete Fourier transform of y(t) can be viewed as the Fourier trans-

form of an unlimited time history record v(t) multiplied by a rectangular

time window u(t) where

u(t) =



1 0 ≤ t ≤ T

0 otherwise.

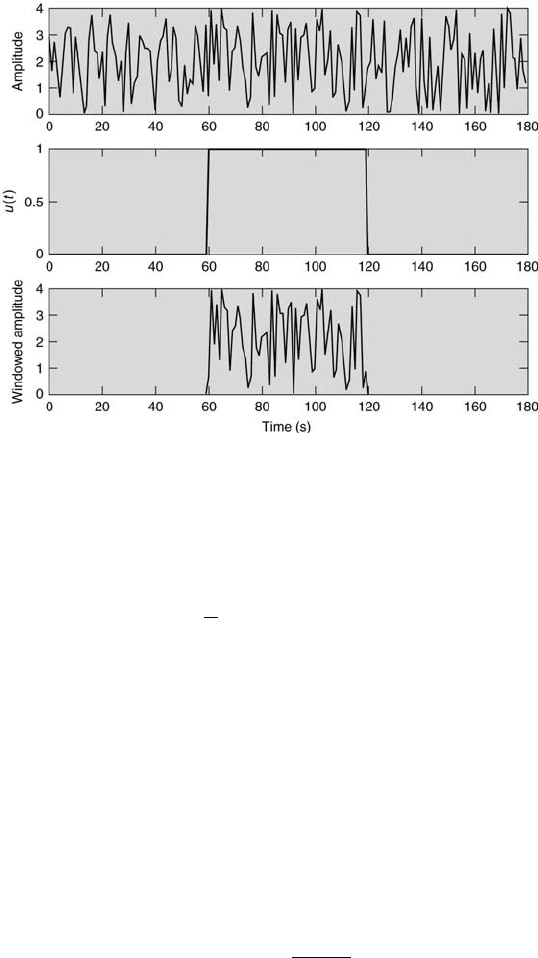
400 Measurement and Data Analysis for Engineering and Science

FIGURE 10.20

Rectangular windowing.

This is illustrated in Figure 10.20. Now,

(f, T ) =

(t) exp[−i2πft]dt, (10.17)

which leads to

Y (f) =

∞

−∞

U(α)V (f − α)dα. (10.18)

This is the convolution integral [3]. So, the Fourier transform of y(t), Y (f),

is the convolution of the Fourier transforms of u(t) and v(t), which are

denoted by U(α) and V (f − α), respectively. For the present application,

u(t) represents the windowing function and y(t) is v(t). The record length is

denoted by T . Various windowing functions can be used. They yield diﬀerent

amounts of leakage suppression.

The rectangular windowing function u

rect

(t) has the Fourier transform

rect

(f), given by

rect

(f) = T



sin πft

πft



. (10.19)

The relatively large side lobes of |U (f)/U (0)| produce a leakage at frequen-

cies separated from the main lobe. This produces a distortion throughout the

spectra, especially when the signal consists of a narrow band of frequencies.

This is illustrated in Figure 10.21.

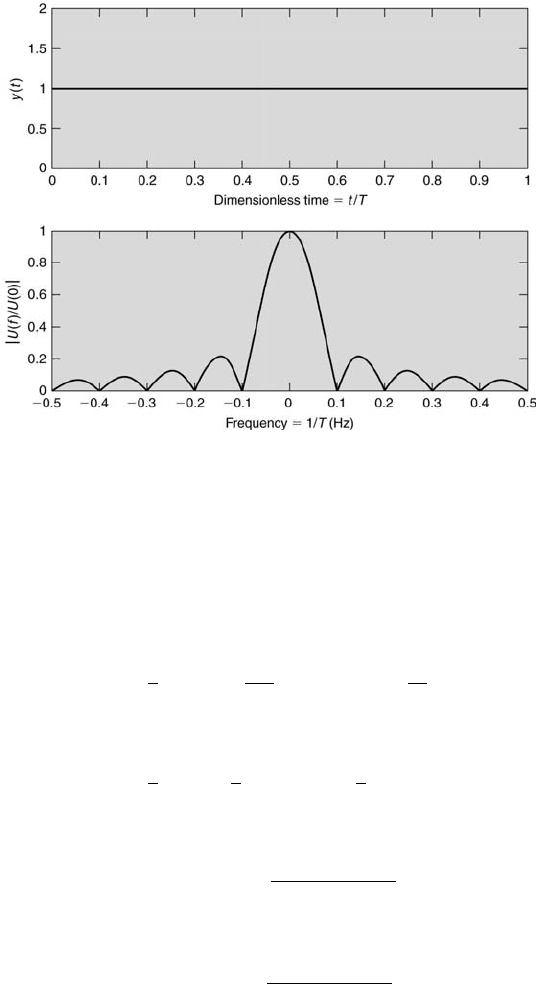
Signal Analysis 401

FIGURE 10.21

The rectangular (boxcar) window.

It is better to taper the signal to eliminate the discontinuity at the

beginning and end of the data record. There are many types of tapering

windows available. The cosine-squared window, also known as the Hanning

window, is used most commonly. This is given by

hanning

(t) =



1 − cos

2πt



= 1 − cos



πt



(10.20)

when 0 ≤ t ≤ T . Otherwise, u

hanning

= 0. Further,

hanning

(f) =

U(f) +

U(f − f

) +

U(f + f

), (10.21)

where f

= 1/T and U(f ) is deﬁned as before with

U(f − f

) = T



sin π(f −f

π(f − f



(10.22)

and

U(f + f

) = T



sin π(f + f

π(f + f



. (10.23)

The Hanning window is presented in Figure 10.22.

Finally, it should be noted that windows reduce the amplitudes of the

spectrum. For a given window, this loss factor can be calculated [2]. For

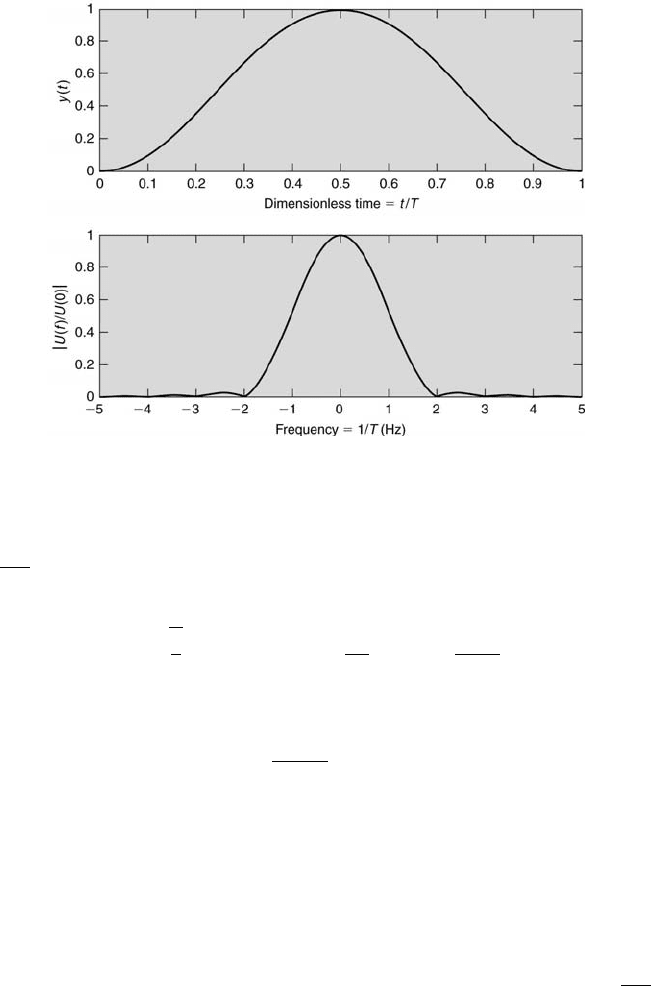
402 Measurement and Data Analysis for Engineering and Science

FIGURE 10.22

The Hanning window.

the Hanning window, the amplitude spectrum must be scaled by the factor

8/3 to compensate for this attenuation. Thus,

) = δt

N−1

n=0



1 − cos

πn



exp



−i

2πkn



, (10.24)

with f

= k/(N δt), where k = 0, 1, 2, . . . , N/2 and

) =

Nδt

i=1

. (10.25)

The recommended procedure [2] for computing a smoothed amplitude

spectrum is the following:

1. Divide data into n

blocks, each of size N = 2

2. Taper the data values in each block {y

} (n = 0, 1, 2, . . . , N − 1) with a

Hanning or other window.

3. Compute the N-point FFT for each data block yielding Y

), adjusting

the scale to account for the tapering loss (for example, multiply by

8/3

for the Hanning window).

4. Compute G

) for n

blocks.

Signal Analysis 403

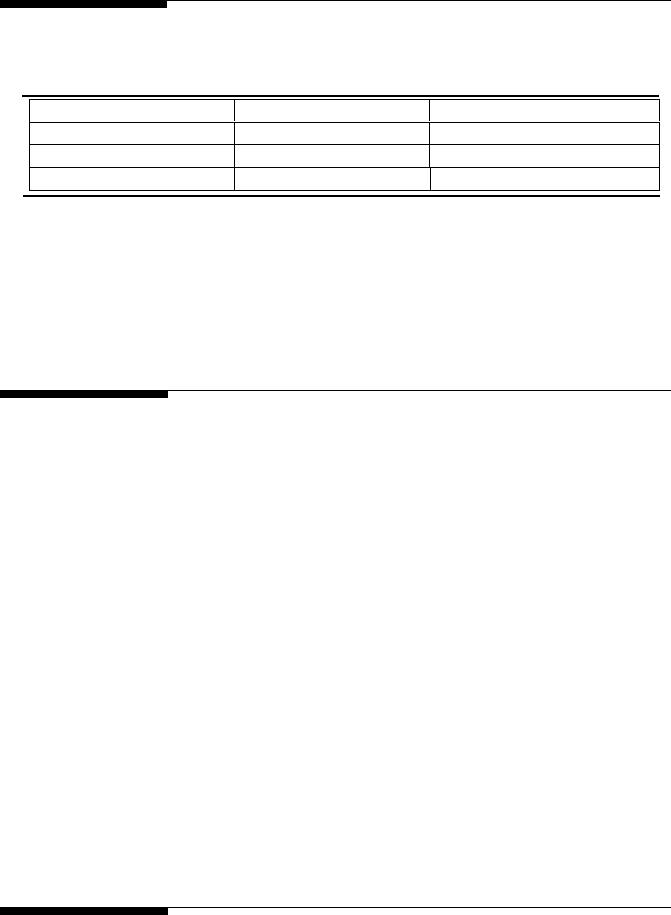
10.8 Problem Topic Summary

Topic

Review Problems

Homework Problems

Sampling

1, 2, 5

1, 2, 3, 4, 5, 6, 7, 8, 9

Aliasing

2, 3, 4, 5, 6, 7, 8, 9,

Amplitude Ambiguity

2, 4, 7, 9

TABLE 10.1

Chapter 10 Problem Summary

10.9 Review Problems

1. Determine the number of discrete frequencies from the minimum to and

including the maximum frequency that will appear in an amplitude-

frequency plot of a signal sampled every 0.2 s. The signal’s minimum

frequency is 0.5 Hz.

2. Determine the frequency resolution of a signal sampled 256 times for a

period of 4 s.

3. Does windowing of a signal produce a signal with no amplitude distor-

tion?

4. Determine the aliased frequency, in Hz, of a 100-Hz sine wave sampled

at 50 Hz.

5. The frequency resolution, in Hz, of a signal sampled 256 times for a

period of 4 s is (a) 256 (b) 1/4, (c) 4/256, or (d) 4.

10.10 Homework Problems

1. A discrete Fourier transform of the signal B(t) = cos(30t) is made to

obtain its power-frequency spectrum. N = 4000 is chosen. Determine

(a) the period of B(t) (in s), (b) the cyclic frequency of B(t) (in Hz),

404 Measurement and Data Analysis for Engineering and Science

resolvable frequency, f

max

(in Hz). Finally, (e) if N = 4096 was chosen

instead, would the computations of the Fourier transform be faster or

slower and why?

2. Using a computer program written by yourself or constructed from avail-

able subroutines, calculate and plot the following: one plot containing

the continuous signal y(t) and its discrete version versus time, and the

other plot containing the amplitude spectrum of the discrete sample.

Provide a complete listing of the program. Do this for each of the cases

below. Support any observed aliasing or leakage of the sample by appro-

priate calculations. State, for each case, whether or not aliasing and/or

leakage occur. The continuous signal is given by

y(t) = 5 sin(2πt + 0.8) + 2 sin(4πt) + 3 cos(4πt) + 7 sin(7πt).

The cases to examine are (a) N = 100, T = 10 s, (b) N = 100, T =

18 s, (c) N = 100, T = 20 s, (d) N = 100, T = 15 s, and (e) N = 50,

T = 15 s, where N represents the number of sample points and T the

sample period.

3. Consider the signal y(t) = 5 + 10 cos(30t) + 15 cos(90t). Determine (a)

the frequencies (in Hz) contained in the signal, (b) the minimum sample

rate (in samples/s) to avoid aliasing, and (c) the frequency resolution

of the frequency spectrum if the signal is sampled at that rate for 2

seconds. Finally, sketch (d) the amplitude-frequency spectrum of y(t)

and (e) the amplitude-frequency spectrum if the signal is sampled at 20

samples/s.

4. A velocity sensor is placed in the wake behind an airfoil subjected to a

periodic pitching motion. The output signal of the velocity transducer

is y(t) = 2 cos(10πt) + 3 cos(30πt) + 5 cos(60πt). Determine (a) the

fundamental frequency of the signal (in Hz), (b) the maximum frequency

of the signal (in Hz), (c) the range of acceptable frequencies (in Hz) that

will avoid signal aliasing, and (d) the minimum sampling frequency (in

Hz) that will avoid both signal aliasing and amplitude ambiguity if 20

samples of the signal are taken during the sample period. Finally, if

the signal is sampled at 20 Hz, determine (e) the frequency content of

the resulting discrete series, y(δnt), and (f) the resulting discrete series

y(δnt).

5. The signal y(t) = 3 cos(ωt) has a period of 4 seconds. Determine the

following for the signal: (a) its amplitude, (b) its cyclic frequency, (c)

the minimum sampling rate to avoid aliasing, (d) its mean value over

three periods, and (e) its rms value over two periods. The formula

[cos(ax)]

dx =

[−

cos(ax) sin(ax) +

ax] may or may not be useful.

Signal Analysis 405

6. At what cyclic frequency will the signal y(t) = 3 sin(4πt) appear if (a)

= 6 Hz, (b) f

= 4 Hz, (c) f

= 2 Hz, and (d) f

= 1.5 Hz?

7. For the deterministic signal y(t) = 2 + 3 sin(6πt) + 4 sin(18πt), sketch

the amplitude-frequency spectrum of y(t) (a) when the signal is sampled

at a rate of 24 Hz (indicate by solid lines) and (b) when it is sampled

at a rate of 12 Hz (indicate by dashed lines). Finally, (c) determine

the minimum sample period (in s) to avoid amplitude ambiguity in the

amplitude-frequency spectrum.

8. At what cyclic frequency will the signal y (t) = 12 cos (3πt) appear if

sampled at (a) f

= 6 Hz, (b) f

= 2.75 Hz, (c) f

= 3 Hz, and (d)

= 1 Hz?

9. Consider the signal z(t) = 3 cos(8πt) + 4 sin(5πt + 0.25). (a) Classify the

signal by its main division plus all subdivisions (for example, nondeter-

ministic/stationary/ergodic). Next, determine (b) the cyclic frequency

of each component, (c) the shortest sample period to avoid amplitude

ambiguity, and (d) the minimum sampling rate to avoid aliasing. Finally,

determine, if any, (e) the aliased frequencies if the signal is sampled at

7 Hz.