Пассмор Дж. Сто лет философии

Подождите немного. Документ загружается.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

прагматизма» (1912) Сорель приветствовал Джеймса как союзника по борьбе со «сциентизмом».

Джеймсу, как считал Сорель, нанесли урон его собственные европейские защитники, а потому в

его философии нередко видели «маловажную заокеанскую выдумку». Целью Сореля было

показать пригодность прагматизма как оружия в борьбе. Как и у Дьюи, прагматизм выливается

здесь в социальную философию, а сегодня прагматизм наиболее энергично отстаивается именно в

работах представителей социальной теории.

Глава 6. НОВЫЕ РАЗРАБ ОТК И В ЛОГИКЕ

Британские эмпиристы были единодушны в своем осуждении формальной логики. Они

полагали, что если бы она и представляла собой какой-нибудь интерес, то лишь как «искусство

мышления», но, заявляли они, мышление не нуждается в искусстве, оно осуществляется

наилучшим образом, когда довольствуется простым скольжением по естественным очертаниям

своего предмета без обращения к каким-либо формальным правилам. Поэтому на протяжении

XVII и XVIII столетий формальная логика едва ли играла заметную роль в интенсивной

философской жизни Британии, хотя в Оксфорде, этом последнем убежище средневековья,

студенты младших курсов все еще вынуждены были уделять ей некоторое внимание. Джоуэтт

говорил о логике, что она не искусство и не наука, а трюкачество. Это дает более или менее

точное описание преподаваемой логики или, скорее, той манеры механического запоминания, что

практиковалась в Оксфорде, где в качестве учебника использовался «Artis Logicae Compendium»

Олдрича (1691), представляющий собой мешанину специальных терминов, аккуратно поданных в

мнемонических виршах для лучшего запоминания незаинтересованными студентами, для которых

логика до 1831 г. была обязательным предметом.

Именно на этом мрачном фоне ярко заблистали «Элементы логики» Уэйтли (1826). Уэйтли

ограничился тем, что по-новому изложил и защитил традиционную логику. Но его изложение

оказалось достаточно ярким, чтобы оживить дух логики после педантизма Олдрича. И защита

была мощной: согласно Уэйтли, эмпиристское опровержение логики основывается на

неправильном понимании ее природы и целей вкупе с чрезмерным уважением к возможностям

невооруженного здравого смысла. Уэйтли мог с полным правом утверждать в последующих

изданиях своей «Логики», что его работа во многом способствовала заметному возрождению

интереса к логическим исследованиям.

Сэр Уильям Гамильтон использовал свой огромный авторитет в тех же самых целях.

Нынешний историк логики пренебрежительно отзывается о Гамильтоне как о «педантичном

шотландском баронете», однако современники видели в нем безусловно величайшего ученого и,

возможно, величайшего философа своего времени. Буль, от которого можно было бы ожидать

недоброжелательной критики, писал в 1847 г.: «О сэре Гамильтоне нельзя говорить иначе как с

уважением, которого он заслуживает благодаря своему таланту и учености». Когда Гамильтон не

только превозносил до небес изучение логики, но и предвещал приближающийся век великих

логических открытий, это производило сильное впечатление на его слушателей. Он призывал их

отказаться от «пассивной покорности», с которой многие логики слепо следовали по стопам

Аристотеля; он обращал их внимание на

то, что «многие корректные формы суждения и умозаключения, используемые

повседневно, но игнорируемые старой логикой, открыто признаны сегодня законными; и многие

отношения, прежде скрытые, вышли на свет»

. Это сильно отличалось как от заявления Канта, что

логика, «судя по всему, достигла своего завершения», так от выступления Уэйтли в защиту

силлогизма как единственной формы корректного рассуждения. Логика, как теперь вдруг

выяснилось, может быть не только возрождена, но и создана по-новому.

Наиболее известным из технических новшеств, благодаря которым Гамильтон завоевал

восхищение современников, является «квантификация предиката». Хотя она и не была его

изобретением

и не имела значительных и длительных последствий для дальнейшего развития

логики, однако стала любопытным предзнаменованием того направления, в котором пошло

развитие логики. Согласно традиционной логике, все утверждения могут быть выражены в одной

из следующих «четырех форм»: все X есть Y, ни один X не есть Y, некоторые X есть Y,

некоторые X не есть Y, где предикат ни в коем случае не имеет прикрепленного к нему «знака

количества». В логике Гамильтона, напротив, предикат квантифицирован и основополагающими

считаются такие формы, как все X есть все Y. Следствием этого, по мнению Гамильтона, является

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

сведение суждений к уравнениям — «суждение всегда представляет собой уравнение с субъектом

и предикатом». В традиционной логике количество присваивается субъекту суждения; в «новой

аналитике» суждение устанавливает тождество двух множеств или «классов» объектов. Так, при

всей пресловутой враждебности Гамильтона к математике его квантификация предиката со всей

очевидностью показала, что теория уравнений является основанием логики. Более того, Гамильтон

связывал со своим методом уравнений идеал «логического исчисления» как «системы логических

обозначений... выявляющей пропозициональные и силлогистические формы в их старом и новом

употреблении почти с механической простотой». Таланты Гамильтона уступали его

честолюбивым замыслам, но и простое провозглашение перспектив будущего развития может

иметь исторические последствия.

Революция в логике

началась с появлением «Формальной логики» Де Моргана (1849). О

Де Моргане сейчас говорят мало; логическая традиция впитала в себя его нововведения без имени

автора. Это забвение частично обусловлено тем, что его наиболее революционизирующие идеи

все еще остаются погребенными в «Трудах Кембриджского философского общества»

(«Transactions of the Cambridge Philosophical Society», 1849—1864), если не считать мысли, кратко

суммированные в его «Программе рекомендуемой системы логики» (1860). Его «Формальная

логика» не представляет существенного интереса для сегодняшних логиков; она все еще не

выходит за установленные Аристотелем рамки, хотя сама аристотелевская логика рассматривается

в ней под новым углом зрения.

Посткартезианские философы, как правило, полагали, что рассуждение «связывает идеи».

Де Морган возродил еретическое воззрение Гоббса, считавшего, что логика говорит об «именах»,

т. е. словах. Сегодня Гоббс добавил бы, что логика представляет собой разновидность вычисления;

эти два положения естественным образом взаимосвязаны. Идея, как таковая,

обладает значением, но со словами можно манипулировать без обращения к их значению.

Как только логика определена как теория «имен», сразу напрашивается аналогия с алгебраическим

вычислением.

Но поскольку бытовало мнение, что алгебраические символы всегда выражают

количественные величины или операции над ними, такие, как сложение, аналогия между логикой

и алгеброй не могла зайти слишком далеко. Однако в первые годы XIX столетия английские

алгебраисты расширили прежнюю концепцию алгебры в двух важных направлениях. Прежде

всего, они отбросили идею, что в таком алгебраическом законе, как

а + b = b + а,

а и b обязательно обозначают количественные величины. На место а и b, утверждали они,

можно подставлять все, что угодно, с тем лишь условием, что оно будет удовлетворять этому

закону. В ответ на возражение, что только количественные величины могут удовлетворять этому

закону, поскольку только их можно складывать, они указывали, что знак плюс не обязательно

выражает сложение; он мог бы выражать любое отношение такого рода, что при подстановке его

на место знака плюс закон продолжал бы выполняться. Согласно примеру Де Моргана, знак плюс

мог бы означать «связан с», поскольку если а связано с b, то и b связано с а. Таким образом, а + b

по-прежнему равно b + а.

Де Морган применил этот новый подход к интерпретации связки «есть» в традиционной

логической форме S есть Р, где S и P всегда воспринимались как общие символы, которые можно

заменить любым термином. Однако предполагалось, что связка «есть» имеет фиксированное

значение, хотя и возможны разногласия относительно характера этого значения. Де Морган,

напротив, утверждает, что слово «есть» также представляет собой общий символ, выражающий

любой тип связи между S и Р, удовлетворяющей определенным логическим правилам, например

правилу, гласящему, что если S есть P и P есть R, то S есть R, а также правилу,

устанавливающему, что из двух суждений S есть P и S не есть P только одно может быть

истинным. Де Морган признает, что эти правила вначале были подсказаны логикам привычным

смыслом слова «есть», точно так же, как законы алгебры вначале были продиктованы

математикам их опытом работы с величинами. Но этот факт, по его мнению, важен лишь для

историков; для логики значение слова «есть» заключено в выполняемых им формальных правилах.

Это учение Де Моргана, лишь кратко изложенное в его «Формальной логике», прямо

подводит к теории отношений, разработанной им в статьях для «Кембриджских трудов». Здесь он

утверждает, что слово «есть» выполняет свои логические функции только благодаря тому, что оно

выражает определенный вид отношения, а именно транзитивное отношение. Правильность

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

рассуждения S есть P, P есть Q, следовательно, S есть Q с этой точки зрения не зависит от того,

какое значение имеет слово «есть» — «приписывается», «является тождественным с» или

«согласуется с»; она зависит лишь от того, что «есть» выражает вид отношения, которое

«растягивается», в отличие, скажем, от отношения любви: никак не может быть истинным, что

если А любит В, а В любит С, то А любит С. Согласно

Де Моргану, в логических целях мы можем записать S есть P в чисто символической

форме, подставив вместо «есть» некоторый символ, указывающий лишь, какой вид отношения

предполагается в логическом использовании связки «есть».

Для современных учебников такое разбиение отношений на виды, имеющие различные

логические свойства, стало привычным. Однако Де Морган мог с полным правом сказать о своих

трудах, что в них формулируется «общее понятие отношения и впервые в истории науки понятия

отношения и отношения отношений получают символическое выражение». Отношения должны в

будущем восприниматься серьезно; их нельзя больше низводить до уровня бедных и

непоследовательных «прихлебателей» у качеств. Это поставило под угрозу и традиционное

превосходство силлогизма, поскольку стало очевидным, что силлогистическое рассуждение

являет собой не тип вывода, с которым, как предполагалось, должно согласовываться любое

рациональное мышление, а лишь частный случай более общей разновидности, представленной тем

фактом, что некоторые отношения являются транзитивными.

Логика Де Моргана представляет особый интерес еще в одном отношении — как попытка

применения новшеств, введенных в теорию вероятностей такими математиками, как Лаплас. Де

Морган не согласен, что логика должна ограничиваться доказательством. «Я не могу понять, —

пишет он, — почему последствия, которые имеет для заключения неполная вера в посылки,

должны изучаться отдельно от последствий, посылки которых считаются абсолютно истинными».

Он не хочет этим сказать, что логику следует трактовать на манер Милля как теорию открытия.

Открытие не зависит от правил — об этом он с наибольшей определенностью заявляет в своем

обзоре нового издания трудов Фрэнсиса Бэкона, перепечатанном затем в «Сводке парадоксов»

(1872). Открытие заключается в выдвижении гипотезы и ее последующей проверке; спрашивать,

откуда появилась гипотеза, значит, по мнению Де Моргана, задавать вопрос, на который не

существует ответа. «Если изобретателя гипотезы просят объяснить свой метод, он должен

ответить, как ответил Зира Колберн на заданный ему вопрос о его методе моментального счета.

Бедный мальчик, которого донимали этим вопросом изрядное количество времени, воскликнул в

сильном раздражении: "Бог вложил это в мою голову, но я не могу вложить это в вашу"». Однако

логик, полагает Де Морган, может оценить вероятность гипотезы, трактуемую как степень

доверия, с которым он может рационально относиться к этой гипотезе.

К счастью, нам нет необходимости детально излагать, какие следствия имело принятие Де

Морганом теории вероятностей Лапласа

. К числу прямых следствий относится его общий тезис о

том, что знанию и верованию можно «приписать числовое значение». В этом аспекте объяснения

вероятности заключены очевидные трудности для Де Моргана, которому не удалось достичь

надежного равновесия между психологией и математикой. По его мнению, вероятность никогда не

бывает «объективной», т. е. является верование вероятным или нет — зависит не от каких-либо

характеристик самих фактов, а от «состояния нашего ума». Но в то же время Де Морган признает,

что вероятность верования нельзя отождествлять с той степенью

доверия, которую нам, отдельным индивидам, случилось проявить к нему. Вероятность

верования — это доверие к нему, которое мы должны иметь или имели бы, будь мы абсолютно

рациональны. Эту уступку многие последователи Де Моргана считали равнозначной отказу от

«психологической» или «субъективной» теории вероятностей. Со времени Де Моргана разработка

более удовлетворительной теории вероятностей всегда шла параллельно с развитием

«математической», или «символической», логики.

Эта логика стала принимать знакомые современному взгляду очертания в творчестве

Джорджа Буля

. Именно с Буля началась непрерывная история современной формальной логики.

Как и Де Морган, Буль был математиком, и поэтому он смотрел на логику глазами алгебраиста,

что особенно заметно в его первой публикации «Математический анализ логики как очерк

исчисления дедуктивных рассуждений» (1847), где логика представлена как вид алгебры, а именно

неколичественной алгебры.

Прежде всего, логика является алгеброй «классов», определяемых как «отдельные

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

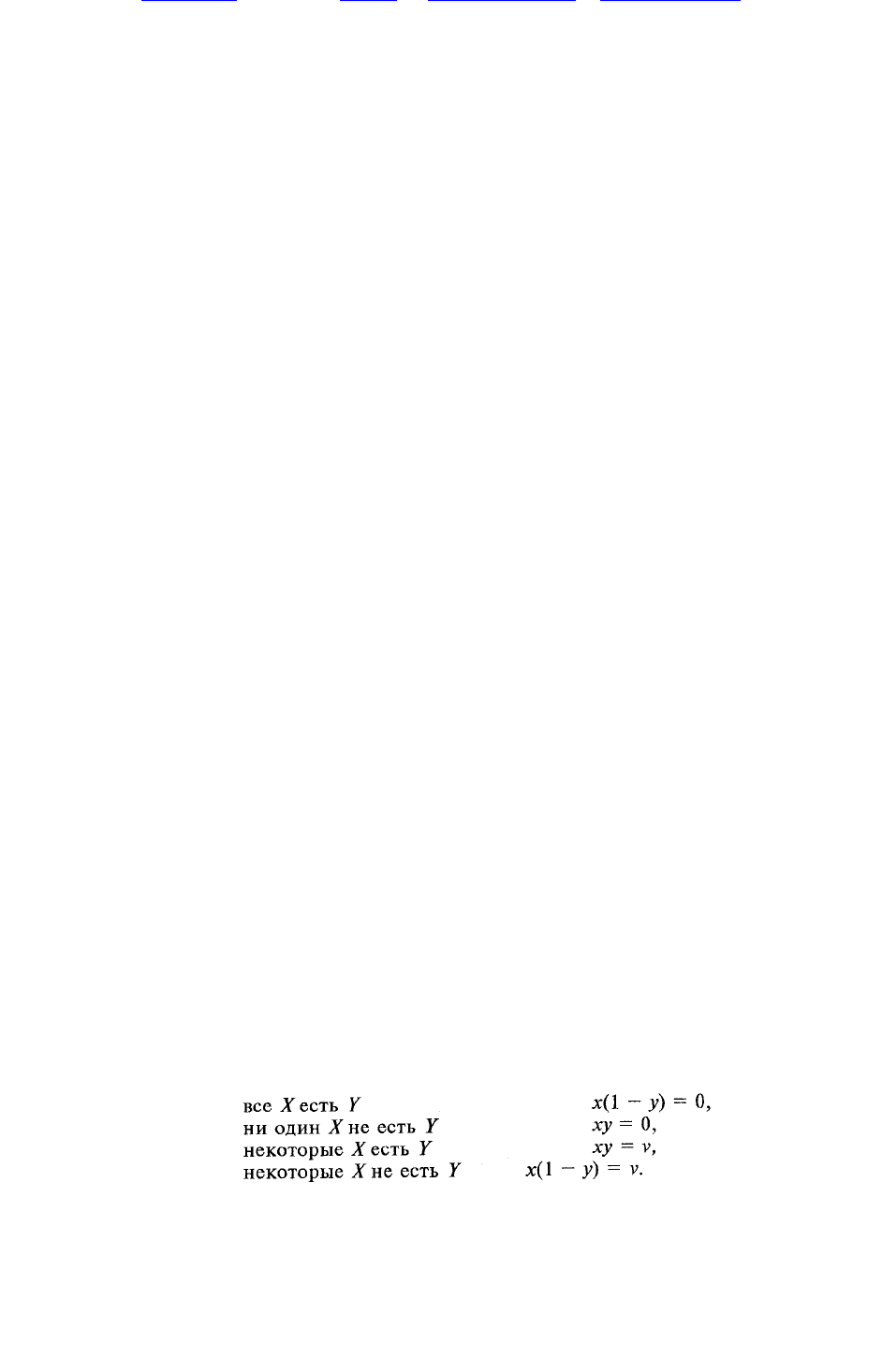
Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

предметы, объединенные под общим именем», и тех способов отбора и объединения классов,

которые Буль считал основанием логического вывода. По его мнению, если мы проанализируем

эти способы, то сразу увидим, что определенную их часть можно описать с помощью известных

алгебраических законов. Например, мы заметим, что не имеет значения, извлечем ли мы вначале

из некоторого класса все предметы X, а затем из полученного класса отберем все Y, или же,

вначале отобрав все Y, мы затем извлечем из них все X. Представляя способ отбора X или

результат отбора (что будет иметь те же последствия) в виде символа х, а способ отбора Y в виде

символа у, Буль выражает тот факт, что порядок отбора не имеет значения, с помощью

следующего уравнения:

ху = ух.

Например, класс млекопитающих, являющихся четвероногими, тождествен классу

четвероногих, являющихся млекопитающими.

Аналогичным образом, отмечает Буль, не имеет значения, извлекаем мы X из какого-то

одного класса или из тех классов, что образуют этот исходный общий класс. Класс, включающий

четвероногих во всем мире, тождествен классу четвероногих Южного полушария, объединенных с

четвероногими из Северного полушария. Этот факт Буль выражает символически так:

х(т + п) = хт + хп.

Пока что речь шла о законах, выполняемых как в количественной алгебре, где х, у, m и п

обозначают числа, так и в логической алгебре, где эти же символы выражают классы. Но в

логической алгебре Буля имеются и другие законы, которые уже не выполняются в обычной

количественной алгебре. Предположим, что мы сначала отобрали всех четвероногих среди

млекопитающих, а затем из созданного таким образом класса четвероногих вновь отобрали

четвероногих. Очевидно, что класс четвероногих остался тем же самым, ничуть не больше того,

каким он был вначале. Этот факт Буль символически выражает так:

х х х = х

или в более общем виде:

= х.

Это уже определенно не закон той алгебры, которую мы изучаем в школе. Появление

такого странного принципа не останавливает Буля от дальнейших поисков алгебраических

аналогий, хотя для его предшественников подобные странности всегда были серьезным

препятствием. Дело в том, что с таким же феноменом, когда алгебраические законы выполняются

только в ограниченной области исследования, уже столкнулись в теории кватернионов,

разработанной незадолго до этого (в 1843 г.) ирландским математиком Гамильтоном, которого не

следует путать с шотландским философом сэром Уильямом Гамильтоном. К тому же, как отмечает

Буль, закон

= х

можно истолковать количественно, если мы сформулируем правило, устанавливающее, что х

должен быть равен 1 или 0. «Законы мышления» — так Буль называет теперь свои

фундаментальные уравнения, — по существу, тождественны законам «двузначной алгебры».

Как полагал Буль, открытие этой тождественности не было простым математическим

курьезом; оно позволило создать метод выведения и проверки следствий из повседневных

высказываний. Однако сначала эти высказывания следует преобразовать в уравнения. Исходя из

того, что «четыре формы» традиционной логики составляют основные типы высказываний, Буль

представил их следующим образом:

Здесь символ «1» означает «универсум»*, а выражение 1 - у — то, что останется, когда все

у будут изъяты из этого универсума. Символ v труднее истолковать. Буль определяет его как класс

с некоторым неопределенным числом элементов. Так,

ху = v

означает, что имеется класс с некоторым числом элементов, содержащий как х, так и у.

Буль считает символ v полезным для вычислений, поскольку с ним можно манипулировать по тем

же правилам, что и с символами х и у.

* В дальнейшем Буль позаимствует у Де Моргана понятие «универсума рассмотрения»,

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

определяемого как область значений, которой ограничено любое высказывание. Например, предложение

«Гамлет пользуется меньшим уважением, чем Фальстаф» — с этой точки зрения отсылает к «универсуму

беллетристики», в то время как «Гладстон пользуется меньшим уважением, чем Дизраэли» указывает на

«реальный» мир истории, а не на «мир вымысла». Предполагается, что каждое высказывание неявным

образом отсылает к универсуму, в котором оно является или истинным, или ложным. Поэтому в более

поздних работах Буля символ «1» используется для обозначения «универсума рассмотрения», а не просто

«универсума».

Фактически в дальнейшем он использовал этот символ со все большей свободой,

предпочитая символически представлять высказывание все X есть Y в виде уравнения:

х = vy

(что можно истолковать как утверждение о тождественности х неопределенной части у)

вместо более понятного уравнения:

х(1 - у) = 0.

Его последователи, наоборот, предпочитали обходиться без символа v, поскольку его

использование приводило к неуклюжим и неинтерпретируемым выражениям. Используя наряду с

равенствами неравенства, они записывали некоторые X не есть Y в виде:

х(1 - у) ≠ 0

вместо:

х(1 - у) = v.

Эта чисто техническая сторона дела имеет определенное значение для понимания метода

Буля. Его метод состоял в вычислении следствий из некоторого множества высказываний,

представленных как уравнения в двузначной алгебре, с помощью обычных алгебраических

методов (с учетом имеющихся ограничений) и с последующей переинтерпретацией результата в

логических терминах. Буля нисколько не беспокоило, что на различных этапах этого анализа

следствий появлялись уравнения, которые нельзя было напрямую истолковать в логических

терминах. Иными словами, он обращался с логикой как с чистой алгеброй; однако немногие из его

последователей оказались готовы перенять эту манеру.

Начав с алгебры, где буквенные символы обозначали классы, Буль вскоре увидел

возможность альтернативных интерпретаций для нее. Он приводит предложение если А есть В, то

С есть D, к сокращенному виду: если X истинно, то Y истинно, где X и Y обозначают не классы, а

высказывания. Затем, переинтерпретировав символы 1, 0 и х в своей алгебре таким образом, что 1

стал означать «все рассматриваемые случаи», х — «случаи, когда X истинно», а у — «случаи,

когда Y истинно»*, Буль представил если X истинно, то Y истинно в виде уравнения

х(1 - у) = 0,

которое теперь истолковывается как: не существует случая, когда X истинно, a Y ложно.

Аналогично, считает Буль, можно представить в виде уравнений

* Позже Буль отмечал, что использование выражения «случаи, когда X истинно» сопряжено с

определенными трудностями, ибо представляется очевидным, что высказывание может быть или истинным,

или ложным и не может быть истинным в одних случаях и ложным в других. Однако, по его мнению,

высказывание вида А есть В, когда оно используется в выражении если А есть В, всегда содержит ссылку на

конкретное время и поэтому символ х следует истолковывать как периоды, когда X истинно, а символ «1» —

как Вечность. Возможно, на Буля оказала влияние предложенная Гамильтоном — математиком, а не

философом — интерпретация алгебры как теории временных отношений.

и алгебраически разложить и другие предложения, в которые мы соединяем высказывания.

Так, он первым обратил внимание на то, что один и тот же логический анализ может быть

применен и к классам, и к высказываниям.

Впоследствии Буль расценил издание своей первой книги как «непродуманный» шаг.

Очевидно, он винил себя за то, что поддался, как он писал, «слишком сильному влиянию

математических идей». Этот недостаток он постарался исправить в «Исследовании законов

мышления» (1854), а еще более явным образом — в рукописях и статьях (1847—1862), вошедших

в «Исследования по логике и теории вероятностей» (1952). Буль доказывал, что логика является

разделом алгебры, и в то же время утверждал, что она формулирует «законы мышления», которым

должны подчиняться, будучи по своей природе доказательством, математические исчисления. Ему

не удалось найти полностью удовлетворивший его способ преодоления трудностей, связанных с

этой точкой зрения. Метафизические разделы в «Законах мышления» не образуют органического

единства с его алгеброй и выглядят чужеродными вставками, однако именно алгебра составила его

вклад в логику, а все его последующие размышления остались незавершенными и не оформились

в публикации.

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

«Законы мышления» и более поздние статьи Буля содержат еще один важный технический

результат, связанный с использованием символической логики для оценки вероятностей, в

частности, для решения задач следующего вида: пусть вероятность события X равна р, а события Y

— q, нужно определить вероятность некоторого события Z на основе его отношения к X и Y. Буль

не утверждает, что задачи такого рода можно решить с помощью одной логики, не прибегая к

количественной математике. Но он подчеркивает важность определения логических отношений

между рассматриваемыми событиями до любых попыток дать количественную формулировку

решения. Выделив логические аспекты проблемы, Буль привлек внимание к серьезным недочетам

в математических теориях вероятностей, сформулированных Лапласом и вполне удовлетворявших

использовавшего их Де Моргана

Некоторый исторический интерес представляет еще один аспект теории вероятностей

Буля. Изначально теория вероятностей разрабатывалась для оценки шансов в азартных играх. В

таком виде ее без труда можно было увязать с проблемами, возникающими при определении

степени уверенности, что, собственно, и интересовало Де Моргана. Но интерес Буля был более

глубоким. На него произвела сильное впечатление социальная статистика, собранная Кетле, и его

заинтересовал вопрос — мог бы обществовед, применяя к подобной статистике теорию

вероятностей, делать успешные социальные прогнозы. Помимо типичных задач для игр, где

шарики или карты можно считать вполне автономными, или «независимыми», объектами, теория

Лапласа совершенно не могла справиться с ситуациями, включающими множество разнообразных

факторов, каждый из которых взаимодействует со всеми остальными. Это обстоятельство и

подтолкнуло Буля к поиску более общей теории. «На мой взгляд, необходимость более общей

теории, — писал он, — обусловлена тем, что наблюдение явлений, особенно в социальной сфере,

как правило, дает нам вероятность не просто отдельных событий, а событий со всеми их

конкретными связями, будь то

связи причинные или связи, вызванные стечением обстоятельств». Здесь уже присутствует

один из тех основных мотивов, что определили последующую разработку теории вероятностей в

трудах такого логика и экономиста, как Кейнс.

В Англии творчество Буля послужило отправной точкой для ряда логиков, среди которых

наиболее известными являются У. С. Джевонс

и Дж. Венн. Джевонс завоевал среди

современников репутацию видного логика и методолога; его наиболее простые труды часто

переиздавались и широко использовались в качестве учебников. Он изучал математику под

руководством Де Моргана, но склад его ума не был математическим. Свою цель он видел в том,

чтобы, как он писал в «Чистой логике» (1864), выявить структуру логики Буля, «освободив его

систему от математического одеяния, которое, без преувеличения, совершенно несущественно для

нее». По его мнению, система Буля — это «тень, призрак, отраженный образ логики», и Джевонс

отправляется на поиски ее обнаженной сути

Его логика, утверждает он, имеет ряд явных преимуществ перед логикой Буля: каждый

метод в ней является самоочевидным; ни один метод не дает «неинтерпретируемых или

аномальных результатов», а все выводы строятся с механической легкостью. Эти утверждения

оправданны с той лишь оговоркой, что рекомендуемые им способы вывода, будучи более

простыми для понимания, в высшей степени утомительны и трудоемки. Но изобретательность

Джевонса преодолела и это затруднение: он создал для выполнения необходимых механических

операций вычисляющую машину, которая является предшественницей электронных «мыслящих

машин» нашего времени

Исчисление Джевонса нашло себе не много почитателей. То, что он осуждал в логике

Буля, а именно ее алгебраический характер, как раз и оказалось наиболее плодотворным, хотя и

концепция «механической проверки» самого Джевонса возродилась в последующей логике,

правда в совершенно иной форме — в виде «таблиц истинности». Однако некоторые из его

новшеств имели длительное влияние на развитие формальной логики

. Кроме того, он предложил

«Буля без слез» для подготовки философов-нематематиков; именно логика Джевонса в основном

вошла в учебники конца XIX в. в качестве «математической», или «символической», логики, или,

что то же самое, «логики уравнений».

Некоторые из ее принципов общепризнано, хотя и ошибочно, считались необходимыми

составными частями любой «математической логики». В особенности это относилось к

утверждению Джевонса, что любое высказывание представляет собой вид тождества или, иными

словами, уравнение. Если Де Морган полагал, что схема Гамильтона все X есть все Y содержит в

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

себе два высказывания (все X есть Y и все Y есть X), то Джевонс считал эту схему одиночным

высказыванием (означающим X = Y), хотя и был вынужден с неудовольствием признать, что для

его вычисляющей машины требуется ее трактовка как содержащей два высказывания. В своей

работе «Подстановка подобных как истинный принцип рассуждения» (1869) Джевонс

обрушивается в самых резких выражениях на традиционные «пропозициональные формы».

«Можно без преувеличения сказать, — писал он, — что Аристотель совершил самую большую и

самую прискорбную ошибку во

всей истории науки, когда выбрал этот вид высказывания (все S есть Р) в качестве

подлинного образца для всех высказываний и основал на нем свою систему». Для Джевонса

подлинным типом высказывания является уравнение, а подлинным типом вывода — «подстановка

подобных», основанная на принципе, согласно которому, «в каком бы отношении предмет ни

находился ко второму предмету, в том же самом отношении он находится к тому, что подобно или

эквивалентно этому второму предмету». По отношению к этому принципу силлогизм выступает

простой его иллюстрацией, причем не самой ясной в сравнении с такими рассуждениями, как если

А больше В и В равно С, то А больше С. Такова была «логика уравнений», которую Брэдли и

Бозанкет (в чьих работах не встретишь имени Буля) считали характерной для логической

алгебры

Еще один аспект в творчестве Джевонса встретил горячее одобрение идеалистов, а именно

его энергичная критика Милля. «Я больше не согласен молча терпеть, — писал Джевонс

, —

бремя плохой логики и плохой философии, возложенное на нас Миллем». Он подверг особенно

резкой критике всю концепцию демонстративных индуктивных методов, а в своей книге

«Принципы науки» (1874), выдержавшей великое множество переизданий, разработал

альтернативную теорию научного метода. Главные ошибки Милля, по мнению Джевонса,

вытекают из его веры в возможность открытия «причин», трактуемых как необходимые и

достаточные условия. Такая цель, благочестиво возражает Джевонс, увела бы нас далеко за

пределы нашей способности «проникать в тайну существующих вещей, воплощающих Волю

Создателя». Это связано с тем, пытается он доказать, что наука никогда не идет дальше гипотез,

которые могут иметь большую или меньшую вероятность.

Адаптировав к своим целям излюбленный пример теоретиков вероятностей, Джевонс

уподобляет ученого человеку, стоящему перед урной, которая содержит какое-то количество

шаров. Извлекая шары из урны (каждый шар, согласно этой метафоре, представляет какой-то

факт), ученый замечает определенные регулярности: так, например, из первых десяти

извлеченных шаров три оказались белыми, а семь — черными. Его следующий шаг состоит в

построении как можно большего числа гипотез, согласующихся с этой регулярностью. Затем

ученый, в соответствии с тем, как Джевонс представлял его задачи, должен сравнить вероятности,

которые каждая из гипотез приписывает тому, что последовательность событий будет именно

такой, какой она является. Например, он должен сравнить вероятность того, что три извлеченных

им белых шара являются единственными белыми шарами в урне, с вероятностью того, что

половина шаров — белые, а другая половина — черные или что три десятых шаров — белые, а

семь десятых — черные. В итоге он должен принять гипотезу, имеющую самую большую

вероятность. Джевонс вполне готов признать, что наиболее вероятная гипотеза может оказаться

ложной. Однако, полагает он, тщетно ждать, что мы сможем достичь «достоверности». Этого

никогда не произойдет; мы или действуем, сообразовываясь с вероятностями, или действуем

наугад, но первое, считает Джевонс, как стратегия, лучше.

Джевонс не относился серьезно к критике Булем Лапласа, поэтому в частностях его теория

оказалась зараженной допущениями из лапласов-

100

ского анализа вероятностей. Судя по многим признакам, Джевонс, по существу, лишь

заново сформулировал идею Де Моргана, согласно которой создание гипотезы — это скачок

воображения, а не особый вид вывода и поэтому в остальном «индукция» представляет собой

теорию вероятности. Однако именно в формулировке Джевонса этот анализ научного метода стал

классической «альтернативой Миллю».

Венн

, в отличие от Джевонса, был математиком. Его первая книга «Логика случая»

(1866) занимает важное место в истории теории вероятностей. Он первым

систематически

разработал «частотную» теорию вероятностей, согласно которой «вероятность» того, что

некоторое событие имеет определенную характеристику, рассматриваемую как свойство самого

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

события, то есть как нечто совершенно отличное от испытываемых наблюдателем чувств

уверенности или сомнения, заключается лишь в том, что определенный процент событий этого

вида имеет данную характеристику. Например, утверждать, что монета упадет орлом вверх с

вероятностью, равной 1/2, значит утверждать, согласно этой точке зрения, что в бесконечной

серии бросаний половина монет упадет орлом вверх.

Однако «частотному» анализу вероятности стали отдавать предпочтение не раньше

второго десятилетия нашего века, да и сейчас он обставлен множеством оговорок и омрачающих

сомнений. В случае Венна непосредственным следствием нового взгляда на вероятность был его

отказ трактовать индуктивный вывод как приписывание оцененной вероятности, поскольку,

согласно его объяснению, любая такая оценка уже сама констатирует единообразие: утверждение,

что в разных совокупностях подбрасываний определенный процент монет упадет орлом вверх,

столь же мало или сильно нуждается в индуктивном обосновании, как и, скажем, утверждение

«все люди умирают». Таким образом, вероятность играет очень ограниченную роль в методологии

Венна, как она изложена в его работе «Принципы эмпирической или индуктивной логики» (1889),

по большей части представляющей собой пространный комментарий к «Системе логики» Милля.

Наиболее важную особенность «Эмпирической логики» составляет обосновываемое

Венном положение, что индуктивные методы Милля опираются на допущение, согласно которому

нам уже известны возможные причины исследуемого нами события. «Предполагается, что число

претендентов на эту роль, — пишет он, — должно быть конечным и все их имена должны быть

заранее нам представлены, так что в нашу задачу входит лишь принять решение относительно их

соответствующей пригодности». И мы, утверждает Венн, не можем доказать ни того, что они

являются единственными претендентами, ни даже того, что мы исключили наименее достойных

кандидатов. Подобно Джевонсу, Венн подчеркивает, что в этих вопросах мы всегда рискуем

ошибиться. Фактически он приобрел репутацию . скептика.

«Символическая логика» Венна (1881) не представляет собой особенно оригинального

вклада в формальную логику, хотя применяемые в ней методы графического представления

обрели достойное существование в виде «диаграмм Венна». Скорее в ней скрупулезно прослежено

развитие символической логики вплоть до момента выхода книги в свет. В этой работе впервые

Венн пытается соотнести творчество Буля с его во многом забы-

101

тыми континентальными предшественниками и с его американскими и немецкими

последователями. Так, с Венна берет начало тенденция к образованию единого международного

сообщества символических логиков, которые этим сильно отличаются от современных

философов.

В своем общем подходе к логике Венн следует Булю, и он, в отличие от Джевонса,

понимает, к чему стремился Буль. «Как мне представляется, отдельные реформы Джевонса в русле

нашей Логики, — писал он, — состоят главным образом в устранении из метода Буля всего, что

кажется ему "неясной формой" — "аномальной", "таинственной", "темной и символической".

Именно в этом он, безусловно, достиг наибольшего успеха, но в результате, на мой взгляд, было

отброшено все, что составляет своеобразие и привлекательность системы Буля». Венн проводит

четкое различие между «незначительными реформами» Гамильтона и совершенно новым

подходом Буля к логике; он ясно показывает, что именно означала для Буля «алгебра» и как мало

осталось в его теории от «квантификации». Фактически впервые благодаря Венну алгебра Буля

предстала как связная и четко сформулированная логика. В своей трактовке Венн освободил эту

алгебру от математических сложностей Буля, но при этом сохранил самый дух булевского

подхода.

Интересным новшеством в логике Венна является проявившийся в ней

«конвенционализм», который позже завоюет себе множество сторонников. В отличие от

Джевонса, Венн не мечет громы и молнии по поводу злодеяний Аристотеля и традиционных

логиков. Традиционная логика, считает он, является весьма полезным инструментом в

образовании — не в последнюю очередь благодаря тому, что она стоит ближе, чем символическая

логика, к языку и устоявшимся правилам повседневно используемой логики. Но она не может

быть общей логикой, ибо область ее действия, полагает он, неизбежно ограничена.

Конвенционализм Венна можно проиллюстрировать на примере его трактовки «экзистенциальной

нагрузки». С точки зрения символической логики, заявляет он, универсальное суждение не

утверждает существования своего субъекта, в то время как частное — утверждает. Если мы не

истолкуем суждение все X есть Y как утверждающее, что класс предметов, которые являются х,

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

но не являются у, не имеет элементов, а суждение некоторые X есть Y — как утверждающее, что

класс предметов, которые являются х и у, имеет элементы, то полностью разрушится

симметричность символической логики, на которой основана возможность ее обобщений. Венн не

утверждает, что было бы неправильно истолковывать универсальное суждение каким-либо иным

способом; фактически для него допущение традиционных логиков, согласно которому если

суждение все X есть Y истинно, то должен существовать хотя бы один X, стоит ближе по смыслу к

обычному употреблению такого рода суждений. Это лишь вопрос удобства, утверждает он.

Отсюда следует, что символическую логику следует рассматривать как одну из логик, а не как

единственно возможную; она представляет собой метод достижения определенных целей, для

которых не годится традиционная логика, но она не заменяет традиционную логику. Это была

новая нота в полемике того периода.

В последние годы XIX в. в Америке и Англии работало много других логиков

. Так, в

Кембридже Дж. Н. Кейнс, младший коллега Венна, в ра-

102

боте «Исследования и упражнения по формальной логике» (1884) попытался включить

новшества Буля и Венна в систему «традиционной логики». В ходе работы он модифицировал эту

логику, согласовав ее с проведенным Венном анализом экзистенциальной нагрузки. Обсуждая и

разъясняя на примерах тезис о том, что универсальное суждение не утверждает существования

своего субъекта, Кейнс положил начало многим последующим дискуссиям.

Оригинальность и изобретательность Кейнса легко недооценить, поскольку как логик он

оказался в тени другого человека из Кембриджа — У. Е. Джонсона

, который перенял

кейнсовский вариант традиционной логики, но был, в отличие от Кейнса, логиком-философом.

Главный труд Джонсона «Логика» появился лишь в 1921 г., и его рассмотрение уместно отложить

до следующих глав, однако более ранние статьи Джонсона о «Логическом исчислении» («Mind»,

1892) важны как первая формулировка «кембриджской философии», главным образом связанной с

именами Мура и Рассела. Само по себе исчисление Джонсона не должно нас интересовать, будучи

еще одной попыткой разработать в манере Джевонса и Венна механический метод решения

логических проблем. Но для Джонсона главный интерес представляют допущения, лежащие в

основе использования исчислений любого вида. Техническая изощренность всегда отступала для

него на второй план.

По его мнению, мы можем легко недооценить то количество интеллектуального

содержания, которое, как мы предполагаем, заключено в исчислении. Джевонс, к примеру,

полагал, что, как только признан общезначимым один-единственный принцип — «подстановка

подобных», исчисление не нуждается более ни в каких других разумных основаниях. Но

исчисление Джевонса, утверждает Джонсон, опирается на сложный набор допущений; оно, в

частности, предполагает, что каждый символ имеет точно установленное значение, что разные

символы могут обозначать один и тот же объект, что символы, представляющие один и тот же

объект, можно подставлять на место друг друга. Это вынесение на поверхность скрытых

допущений стало отличительной особенностью кембриджского логического анализа.

Равно «кембриджской» является и идея Джонсона о том, что задача логики — это анализ,

т. е. расчленение системы на составляющие ее базисные высказывания (в противоположность

доктрине оксфордских идеалистов, определявших логику как обнаружение системы, включающей

в себя «суждение»). Джонсон признает сложность любого реального высказывания. Однако мы

можем предложить в качестве идеала «молекулярное» высказывание, которое впоследствии

Рассел назовет «атомарным» и которое нельзя уже разложить на другие высказывания, а можно

разбить только на термины, точно так же как молекулу можно расчленить только на атомы.

Согласно Джонсону, каждое высказывание представляет собой множество таких молекулярных

высказываний, соединенных между собой логическими отношениями, признаваемых им

основополагающими и выражающихся словами «и» и «не». «Все, что формальная логика может

сделать при синтезе высказываний, — писал он, — содержится в законах, управляющих

употреблением таких слов, как "и " и "не "».

103

Как только мы осознаем это, считает Джонсон, мы сможем решить проблему, которая

иначе оказалась бы очень серьезной, т. е. мы сможем понять, как возможны факты,

соответствующие гипотетическим и дизъюнктивным высказываниям. Очевидно, что такие

высказывания могут быть истинными, и все же в природе нет ничего, что соответствовало бы

словам «если» и «или». Однако, если мы согласимся истолковать высказывание если р, то q как

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.

Янко Слава (Библиотека Fort/Da) || slavaaa@yandex.ru || http://yanko.lib.ru

отрицающее истинность утверждения р и не-q, а высказывание р или q — как отрицающее

истинность утверждения не-р и не-q, то эти трудности бесследно исчезнут, поскольку, считает

Джонсон, «и» и «не» обозначают «реальные» отношения; при этом слово «не» служит способом

выражения того факта, что предмет обладает свойством, отличным от приписываемого ему, но

название этого свойства не сообщается.

Анализ Джонсона предполагает заметный отход от логической традиции, для которой

«если.., то...» было основополагающим логическим выражением, а умозаключение служило

привычной отправной точкой для логики. Джонсон понимал, что его будут критиковать на том

основании, что наша «мысленная установка», когда мы утверждаем, что если р, то q, сильно

отличается от «мысленной установки», когда мы отрицаем истинность р и не-q, из чего следует,

что эти выражения, говоря языком Оксфорда, являются разными «суждениями». В ответ Джонсон

указывал, что наши «мысленные установки» не имеют никакого отношения к формальной логике,

так как логика — это теория высказываний, определяемых как «выражения истинности или

ложности», а не теория суждений, выражающих, согласно оксфордской трактовке, установки

сознания. Этот акцент на «высказываниях» был типичным для кембриджских логиков.

Тем временем в Америке совершенно оригинальная логика стала вырисовываться в

творчестве Ч. С. Пирса

. Однако уже само многообразие его логических трудов затрудняет их

изложение. Вместе с тем его анализ часто вплотную граничит с невразумительностью. Он был

математиком и сыном математика, поэтому для него не было ничего более понятного, чем

математические символы. «Когда человек заявляет, — писал он Джеймсу, — что не может понять

математику, т. е. не может понять очевидного, то разве вы не видите, что этим он преграждает себе

путь?» Часто Пирс довольствуется изложением голых результатов, в то время как читатели ждут

от него примеров и разъяснений. Это объясняет — наряду с тем фактом, что многие его труды не

были опубликованы до их включения в его «Собрание сочинений» (1931-1935), — почему он

многие вещи лишь предугадал, но не сумел положить начало традиции. На долю других, с их

более медлительной, но зато и более понятной манерой рассуждения, выпало сделать выводы,

которые уже были известны Пирсу, но лишь в результате вспышек интуиции. Это вовсе не

означает, что логики-математики того времени игнорировали его; напротив, они высоко

оценивали его заслуги, и, не будь этого, он вряд ли стал бы известен. Но истинный масштаб его

нововведений ускользнул от их внимания.

Общий характер ранних логических трудов Пирса можно описать следующим образом: он

модифицирует в различных отношениях логическую алгебру Буля, сохраняя ее алгебраический

характер, но проводя четкое различие между ее чисто логическими ингредиентами и тем, что

интерпрети-

104

руемо лишь в математических терминах. Затем он показывает, что в рамках такого

исчисления можно сформулировать улучшенный вариант логики отношений Де Моргана. Таким

образом, он первым объединяет логику Буля и Де Моргана в единую логическую структуру.

Такое описание позволяет предположить, что Пирс был лишь аккуратным

систематизатором. Но нет ничего более далекого от истины, чем это предположение;

отличительной чертой всего творчества Пирса была несомненная оригинальность. Временами

заумный и эксцентричный, он никогда не был заурядным. Два его главных нововведения

заслуживают особого внимания, поскольку в конечном итоге они вошли в основной корпус

философии, правда, не напрямую, а благодаря усилиям других, порой менее значительных

мыслителей.

Первым из этих нововведений является выделение трех видов предикатов, названных им

(«Monist», 1897) «одноместными», «двуместными» и «многоместными». «Одноместный» предикат

входит в предложения такой формы: «... есть человек», которые становятся законченными при

заполнении единственного пропуска. В выражении «... есть возлюбленный ...» имеется два

пропуска, поэтому «есть возлюбленный» является двуместным отношением. А в выражении «...

дает......» или, используя пример, особенно

выделяемый Пирсом, в выражении «... обозначает ... для ...» имеется три пропуска, и

рассматриваемое отношение является многоместным.

Введение многоместных отношений значительно расширило логику отношений — раздел

логики, который, как не уставал подчеркивать Пирс, первым открыл Де Морган. В результате

появилась возможность, полагал он, решить ряд философских проблем, прежде не поддававшихся

решению; в частности, допущение многоместных отношений, считал Пирс, играет решающую

Пассмор Дж. Сто лет философии: Пер. с англ. — М.: «Прогресс-Традиция», 1998. — 496 с.