Pao Y.C. Engineering Analysis: Interactive Methods and Programs with FORTRAN, QuickBASIC, MATLAB, and Mathematica

Подождите немного. Документ загружается.

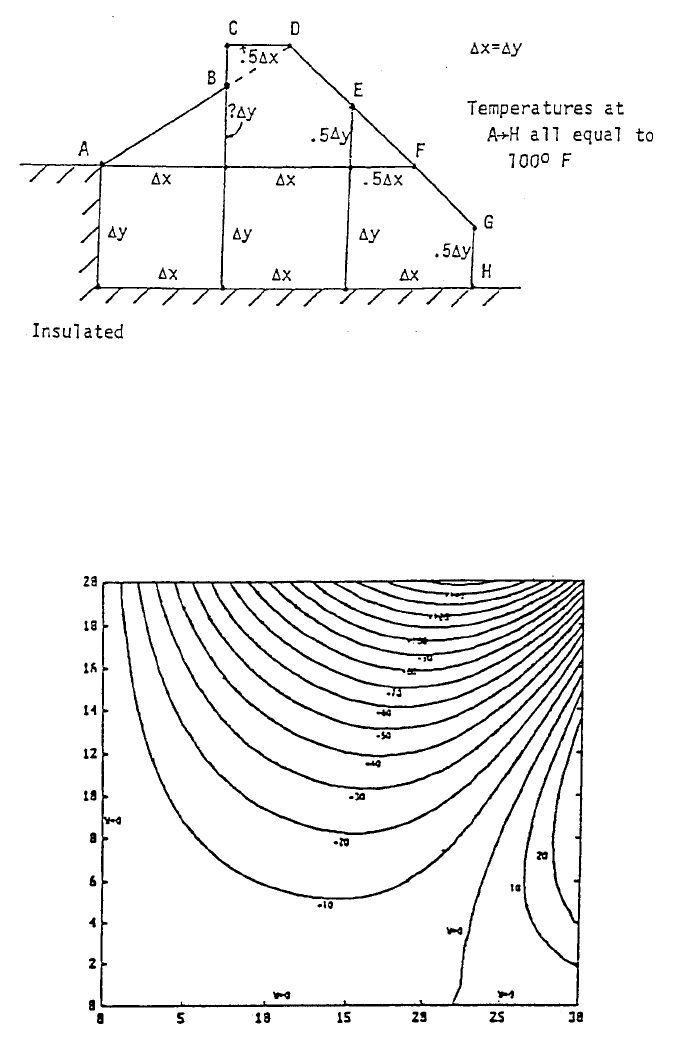
10. The warping of a twisted bar of uniform rectangular cross section already

depicted by the mesh plot shown in Figures 5 and 6 also can be observed

using the contour plotting capability of MATLAB. Apply program Warp-

ing.m and the command contour to generate a contour plot for a = 30 and

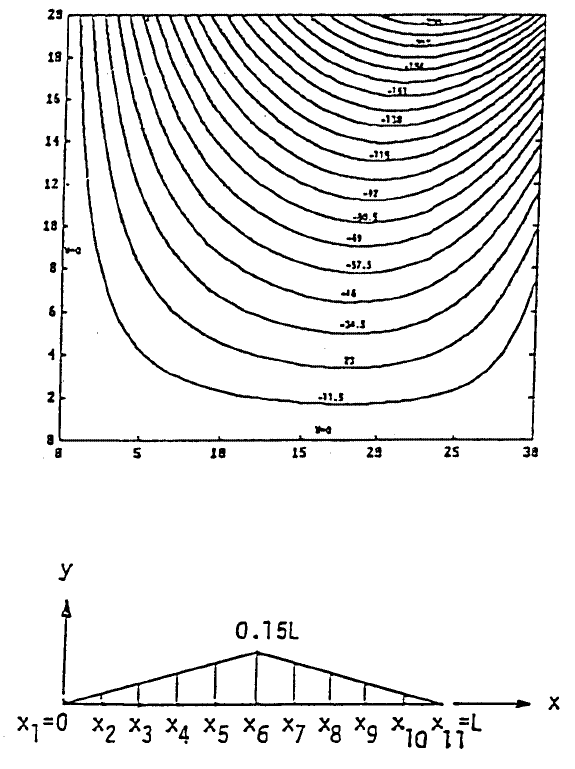
b = 20 using = 100 and = 1 (Figures 14A and 14B, respectively).

FIGURE 13. Prtoblem 7.

FIGURE 14A. Problem 10.

11. Direct solution of the warping function W(X,Y) can also be obtained

following the procedure described in Problem 8. For a rectangular cross

section (-a≤X≤a and -b≤Y≤b) of a twisted rod, the warping W(X,Y) needs

to be found only for the upper right quadrant 0≤X≤a and 0≤Y≤b which

in general can be divided into a gridwork of (M + 1)x(N + 1). The

antisymmetry conditions W(X = 0,Y) = W(X,Y = 0) = 0 reduces to only

(M + 1)x(N + 1)-(M + N + 1) = MxN unknowns, i.e., only solving those

W’s for X>0. That means we have to derive a system of MxN linear

algebraic equations: along the boundaries X = a and Y = b, Equations 23

to 25 are to be used and for the interior grid points (0<X<a and 0<Y<b),

Equation 3 is to be used. Generate such a matrix equation and then apply

FIGURE 14B. Problem 10.

FIGURE 15. Problem 4.

the program Gauss to ﬁnd these MxN W’s. Compare the resulting W

distribution with those obtained by the relaxation method shown in

Figures 5 and 6 for a = 30 and b = 20.

12. Same as Problem 11 except for the case a = b = 20 and for comparing

with Figure 7.

13. Solve the warping problem by Mathematica.

WAVEPDE

1. For the string problem analyzed in the Sample Application, modify the

program slightly so that the times required for the string to have the

magnitudes of its maximum displacements reduced to 0.8, 0.6, 0.4, and

0.2, and the corresponding deﬂected shapes can be printed.

2. Rearrange the subprogram FUNCTION F in the program WavePDE to

consider the case of an initial, upward lifting the mid-third (8≤x≤16 cm)

of the string by 1 cm. Rerun the program using the same input data as in

the Sample Application.

3. Consider a string which is composed of two different materials even

though it is subjected to a uniform tension T so that the left and right one-

thirds (i.e., , 0≤x≤8 cm and 24≤x≤32 cm, respectively) of the string has

a wave velocity a = 80 cm/sec while its mid-third (i.e., 8≤x≤16 cm) has

a wave velocity a = 90 cm/sec. Modify and then rerun program WavePDE

using the other input same as in the Sample Application.

4. A tightened string of length L equal to 1 ft is lifted as shown in 15 and

is released with a velocity distribution v = y(t = 0,x)/t = 2sinx/L in

ft/sec. If the constant T/m appearing in Equation 2 is equal to 8,100

/sec

, use a time increment t = 0.0005 sec and a space increment x =

0.1L and apply Equation 7 to ﬁnd the y values at t = 0.001 sec and for

the stations x

and x

5. In approximating Equation 1 by ﬁnite differences, we may keep the same

approach for 

u/t

as in deriving Equation 7 but to apply the second

central-difference formula for 

u/t

not at t = t

but at t = t

i + 1

. The

resulting equation, for C = (at/x)

, is:

Derive a matrix equation for solving the unknowns u

for j = 1,2,…,N–1,

at t = t

i + 1

. Note that the boundary conditions are u

i + 1,0

= u

i + 1,N

= 0. Write

a program WavePDE.G which uses the Gaussian Elimination method to

solve this matrix equation and run it for the Sample problem to compare

the results.

6. Change the MATLAB m ﬁle WavePDE to solve Problem 4.

7. Apply Mathematica to solve Problem 4.

−++

()

−=−+

+− + ++ −

Cu C u Cu u u

ij ij ij ij ij11 1 11 1

,,,,,

8.6 REFERENCES

1. C. R. Wylie, Jr., Advanced Engineering Mathematics, Chapter 9, Second Edition,

McGraw-Hill, New York, 1960.

2. J. P. Holman, Heat Transfer, McGraw-Hill, New York, 1963.

3. S. Timoshenko and J. N. Goodier, Theory of Elasticity, Chapter 11, Second Edition,

McGraw-Hill, New York, 1951.