Pao Y.C. Engineering Analysis: Interactive Methods and Programs with FORTRAN, QuickBASIC, MATLAB, and Mathematica

Подождите немного. Документ загружается.

program Bairstow to be  = 

= 1.98, 15.5, and 32.5. For  = 1.98 the frequency

 is equal to 1.407 radians/second, the amplitude ratios are C

= 1.80 and C

2.25. The program EigenVib has been developed for generation of the matrix [A]

when the values of the masses, m’s, and the spring constants, k’s, are provided.

FORTRAN VERSION

Sample Application

To demonstrate application of the program EigenODE.Vib, the numerical exam-

ple for the vibration of three masses shown in Figure 1 in Section 7.1 is run to

generate the matrix [A] and then the program CharacEq is used to obtain a char-

acteristic equation 

– 50

– 600 — 1000 = 0. The program Bairstow enables its

roots to be found as equal to 1.9806, 15.550, and 37.470.

It is also of interest to show an application of the programs MatxInvD and

EigenvIt (to be introduced in Section 7.5) for inverting the matrix [C] and then

iteratively ﬁnding the smallest eigenvalue in magnitude (which is related to the

lowest natural frequency of the vibration). The resulting display from using these

two programs is:

The smallest eigenvalue in magnitude of the matrix [A] is therefore equal to

1/0.50489, or, 1.9806 same as obtained by application of the programs CharacEq

and Bairstow.

MATLAB APPLICATIONS

A ﬁle EigenvIt.m for MATLAB has been developed and is listed and discussed

in the program EigenvIt. This function is in the form of [EigenVec,Lambda] =

EigenvIt(A,N,V0,NT,Tol). It accepts a matrix [A] of order N, an initial guessed

eigenvector V0, and tries to ﬁnd the eigenvector Eigenvec and eigenvalue Lambda

iteratively until the sum of the absolute values of the differences of the components

of two consecutive guessed eigenvectors is less than the speciﬁed tolerance Tol. The

number of iterations is limited by the user to be no more than NT times. The reader

should refer to the program EigenvIt for more details, here provide a simple example

of using EigenvIt.m:

The display indicates that for the speciﬁed matrix [A] of order equal to 3, the

largest eigenvalue in magnitude is equal to 5.0000 and its associated eigenvector is

[0.7071 0 0.7071]

after 8 iterative steps. The iteration is terminated when the sum

of the absolute values of the differences of the corresponding components of the

guessed eigenvectors obtained during the seventh and eighth iterations is less than

the speciﬁed tolerance 0.0001.

To ﬁnd the smallest eigenvalue and its associated eigenvector by iteration,

EigenvIt.m also can be applied effectively. Let us use the example in Sample

Applications:

Notice that inv.m of MATLAB has been applied to ﬁnd the inverse of [A] and

using it for EigenvIt.m to ﬁnd the eigenvalue and eigenvector by iteration.

MATHEMATICA APPLICATIONS

For the buckling problem, Mathematica can be applied as follows:

In[1]: = Ns = 5; EI = 1.; L = 1.; H = L/(Ns + 1);

In[2]: = (Print[“Number of Station = “, Ns, “ EI = “, EI, “ Length = “, L,

“Delta L = “, H)

Out[2]: =

Number of Station = 5 EI = 1. Length = 1. Delta L = 0.166667

In[3]: = (Do[Do[If[i == j, M[[i,j]] = 2.*EI/H^2,

If[i == (j + 1)||i = = (j–1), M[[i,j]] = EI/H^2, 0]],

{i,Ns}],{j,Ns}]); MatrixForm[M]

Out[3]//MatrixForm: =

72. 36. 0. 0. 0.

36. 72. 36. 0. 0.

0. 36. 72. 36. 0.

0. 0. 36. 72. 36.

0. 0. 0. 36. 72.

In the next section, we will show how the characteristic equation for the above

derived matrix [M] can be determined by application of Mathematica and subse-

quently how the eigenvalues and eigenvectors are to be obtained.

7.3 PROGRAM CHARACEQ — DERIVATION OF CHARACTERISTIC

EQUATION OF A SPECIFIED SQUARE MATRIX

The program CharacEq is designed to generate the coefﬁcients of the characteristic

equation of an interactively speciﬁed square matrix by use of the Feddeev-Leverrier

method. Such a characteristic equation is needed in the stability, vibration, and other

so-called eigenvalue problems.

Readers interested in these problems should also

refer to the discussions on the programs EigenODE and EigenVec. The former

discusses how the square matrix is to be generated by ﬁnite-difference approximation

of ordinary differential equation. The latter program delineates how the eigenvectors

are to be found by a modiﬁed Gaussian elimination method for each eigenvalue and

how the eigenvalues are to be solved from the characteristic equation by the program

Bairstow. Here for derivation of the characteristic equation, let us denote the speciﬁed

square matrix be [A] and its elements be a

i,j

for i,j = 1,2,…,n with n being the order of

[A]. The Feddeev-Leverrier method ﬁrst express the characteristic equation of [A] as:

(1)−

()

−− −…−−

()

−−

−

nn n

pp ppλλ λ λ

where the coefﬁcients p

through p

are to be determined by the following recursive

formulas:

(2)

and

(3,4)

Equation 4 is to be applied for j = 2,3,…,n. Trace, appearing in Equation 2, of

a square matrix is the sum of the diagonal elements. A speciﬁc, numerical example

will help further explain the details involved in applying the formulas presented

above. Consider a square matrix:

(5)

Then, [B]

= [A] and p

= Trace([B]

) = 0–1+7 = 6. The other p’s and [B]’s are

to be calculated according to Equations 2 and 4, and ﬁnally the characteristic equa-

tion is to be expressed according to Equation 1 as:

and ﬁnally, the characteristic equation is:

B for k n

[]

=…

12 Trace of , , ,

B A and B A B p I

[]

[] []

[][]

−

[]

()

−

[]

=− −

−













023

10 1 2

247

BAB I

[]

[][]

−

[]

()

=− −

−













−

−−

−













−−













[]

()

=− − +

()

023

10 1 2

247

623

10 7 2

241

26 2 7

66 5 30

42 4 9

226592

Trace

−−11

BAB I

[]

[][]

[]

()

=− −

−













−−

−

−−

























[]

()

=++

()

023

10 1 2

247

15 2 7

66 6 30

42 4 20

600

060

006

3 66636

Trace

−

()

−−−

()

=− + − + =161160

λλλ λλλppp

Both QuickBASIC and FORTRAN version of the program CharacEq have

been made available for derivation of the characteristic equation based on the

Feddeev-Leverrier method. The program listings are presented below along with

some sample applications.

QUICKBASIC VERSION

Sample Application

The display screen will show the following questions-and-answers and the com-

puted results when the matrix [A] given in (5) is interactively entered as the matrix,

for which its characteristic equation is to be obtained:

FORTRAN VERSION

Sample Application

MATLAB APPLICATION

MATLAB has a ﬁle called poly.m which can be applied to obtain the charac-

teristic equation of a speciﬁed square matrix. The following is an example of how

to specify a square matrix of order 3, how poly.m is to be called, and the resulting

display:

For the FORTRAN sample problem, we can have:

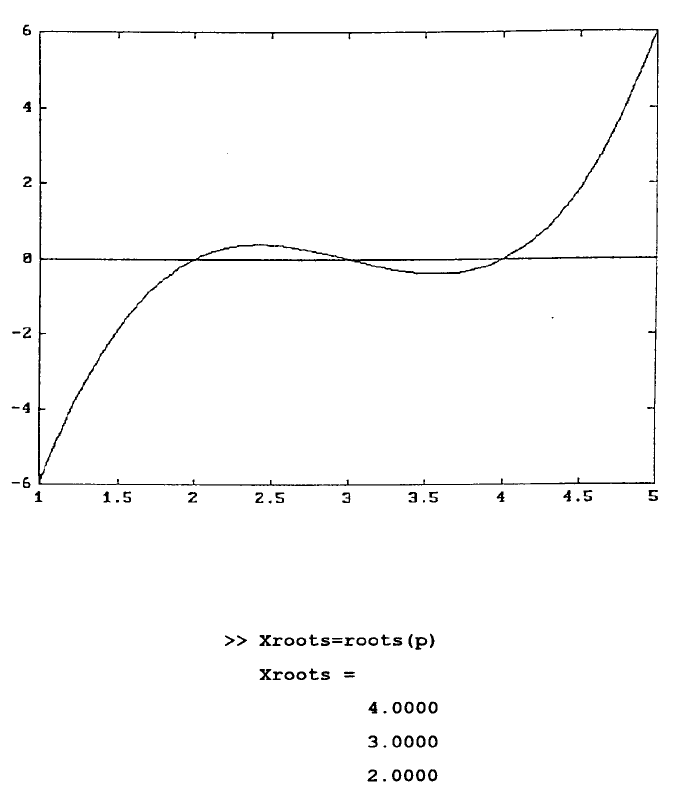
Here, we can apply plot.m and polyval of MATLAB to graphically explore the

roots of this obtained polynomial P(x) = x

–9x

+ 26x–24 = 0 by interactive entering:

>> x = [1:0.05:5]; y = polyval(p,x); plot(x,y), hold

>> XL = [1 5]; YL = [0 0]; plot(XL,YL)

The resulting curve is shown in Figure 3. Notice that the added horizontal line

intercepts the polynomial curve, it helps indicate where the real roots are. To actually

calculate the values of all roots, real or complex, the roots.m of MATLAB can be

applied as follows:

These results complement well with those presented in Figure 3.

MATHEMATICA APPLICATIONS

For ﬁnding the characteristic equation of a given matrix, Mathematica’s func-

tion Det which derives the determinant of a speciﬁed matrix can be employed. To

do so, the matrix should be entered ﬁrst and then Det is to be called next.

Input[1]: =

m = {{0,2,3), {–10,–1,2}, {–2,4,7}}

FIGURE 3.