Pao Y.C. Engineering Analysis: Interactive Methods and Programs with FORTRAN, QuickBASIC, MATLAB, and Mathematica

Подождите немного. Документ загружается.

Since the points are numbered in increasing order from P

through P

and P

it is then clear that X

i + 1

is always less than X

. A

thus carries a minus sign.

Based on the above discussion, the area enclosed by contour C

can therefore

be calculated by

adding

and A

if the numbering of the points selected on the

contour follows a

clockwise

direction. Let the total number of points selected around

the contour C

be denoted as K, then K = N + (M–2) because P

and P

are re-used

in consideration of the bottom branch. Hence, the area enclosed in C

is:

(4)

where the Nth point has coordinates (X

) = (X

) and the ﬁrst and last points

have coordinates (X

) = (X

K + 1

) = (X

). And it should be evident that

in case of a cut-out, such as the contour C

shown in Figure 1(B), the subtraction

of the area enclosed by the cut-out can be replaced by an addition of the value of

the area when it is calculated by using Equation 4 but the numbering of the points

on contour C

is ordered in

counterclockwise

sense.

5.2 PROGRAM NUINTGRA — NUMERICAL INTEGRATION BY

APPLICATION OF THE TRAPEZOIDAL AND SIMPSON RULES

Program

NuIntGra

is designed for the need of performing numerical integration

by use of either trapezoidal rule or Simpson’s rule. These two rules will be explained

later. First, let us discuss why we need numerical integration.

Figure 3 shows a number of commonly encountered cross-sectional shapes in

engineering and scientiﬁc applications. The interactive computer program

NuIntGra

has an option of allowing keyboard input of the coordinates of the vertices of the

cross section and then carrying out the area computation of cross-sectional area

based on Equation 4.

The following gives some detailed printout of the results for the cross sections

shown in Figure 3. It is important to point out that the points on the contours describing

the cross-sectional shapes should be numbered as indicated in Figure 3, namely, clock-

wise around the outer boundary and counterclockwise around the inner boundary

AA A YY X X

=+= +

()

−

()

∑

FIGURE 3.

Commonly used cross sections in engineering and scientiﬁc applications.

By use of a Function subprogram F(X) which deﬁnes the upper branch of a

circle of radius equal to 1 and having its center located at X = 1 as listed below,

program

NuIntGra

also has been applied for calculating the value of



. The screen

display of this interactive run is also listed below after the Function F(X).

QuickBASIC Version FORTRAN Version

FUNCTION F(X) FUNCTION F(X)

F = SQR(1(X-1)^2) F = SQRT(1.-(X-1)**2)

END FUNCTION RETURN

END

More discussion on the accuracy of



will be given later after we have introduced

both the trapezoidal and Simpson’s rules which have already been incorporated in

the program NuIntgra.

RAPEZOIDAL

ULE

Returning to Figure 2, we notice that if in approximating the curve by a series

of linear segments the points selected on the curve are

equally spaced

in X, Equation

2 can be considerably simpliﬁed. In that case, we have:

(5)

and Equation 2 can be written as:

(6)

Or, in a different form for easy interpretation, it may also be written as:

(7)

All the in-between heights, Y

for i ranging from 2 to N–1 that is the next to the

last, are appearing twice because they are shared by two adjacent strips whereas the

ﬁrst and last heights, Y

and Y

, only appear once in Equation 7.



X in Equation 7

is the common width of all strips used in summing the area.

Equation 7 is the well known

Trapezoidal Rule

for numerical integration. In a

general case, it can be applied for approximate evaluation of an integral by the

formula:

∆XXXXX X X

=−=−=…= −

−21 32 1

AXYY

()

−

∑

∆

AXY YY

=++













−

∑

∆

(8)

where the increment in X,



X, is simply:

(9)

when N points are selected on the interval of integration from X

to X

. It should

be understood that in Equation 8 f

is the value of the integrand function f(X)

calculated at X = X

. That is:

(10)

where for i = 1,2,…,N

(11)

(12,13)

Program NuIntGra allows the user to deﬁne the integrand function f(X) by

specifying a supporting Subprogram FUNCTION F(X) and to interactively input

the integration limits, X

and X

, along with the total number of points, N, to

determine the value of an integral based on Equation 8. As an example, we illustrate

below the estimation of a semi-circular area specifying X

= 0, X

= 2, and N = 21

and deﬁning the integrand function f(X) in FUNCTION F(X) with a statement

F = SQRT(1.-(X–1.)*(X–1.))

This statement describes that the center of the circle is located at (1,0) and radius

is equal to 1. When N is increased from 21 to 101 with an increment of 20, the

following table shows that the accuracy of trapezoidal rule is steadily increased when

the estimated value of the semi-circle is approaching the exact value of /2.

SIMPSON’S RULE

The Trapezoidal Rule approximates the integrand function f(X) in Equation 8

by a series of connected straight-line segments as illustrated in Figure 2. These

straight-line segments can be expressed as linear functions of X. A straight line

N21416181101

Area 1.552 1.564 1.567 1.568 1.569

Error 1.21% 0.45% 0.26% 0.19% 0.13%

fXdX Xf f f

()

=++













∫

∑

−

∆

∆XXX N

=−

()

−

()

ffX

≡

()

Xi XX

=−

()

+1 ∆

X X and X X

LNR1

which passes through two points (X

) and (X

i + 1

) may be described by the

equation:

(14)

where m

is the slope and b

is the intercept at the Y-axis of the ith straight line.

Upon substituting the coordinates (X

) and (X

i + 1

) into Equation 14, we

obtain two equations

The slope m

can be easily solved by subtracting the ﬁrst equation from the

second equation to be

(15)

Substituting m

into the Y

equation, we obtain the intercept to be:

(16)

For the convenience of further development as well as for ease in computer

programming, it is better to write the equation describing the straight line as:

(17)

That is to replace m

and b

in Equation 14 by a

and a

, respectively. From

Equations 15 and 16, we therefore can have:

(18)

and

(19)

A logical extension of Equation 17 is to express Y as a second-order polynomial

of X, namely:

(20)

YmXb

Y m X b and Y m X b

iiii i ii i

=+ = +

mYYX X

ii ii i

=−

()

−

()

++11

bYY YXX X

ii i iii i

=− −

()

−

()

++11

Ya aX aX

=+ =

∑

aYYXX

iii i

=−

()

−

()

aYY YXX X

ii iii i

=− −

()

−

()

Ya aXaX aX

=+ + =

∑

01 2

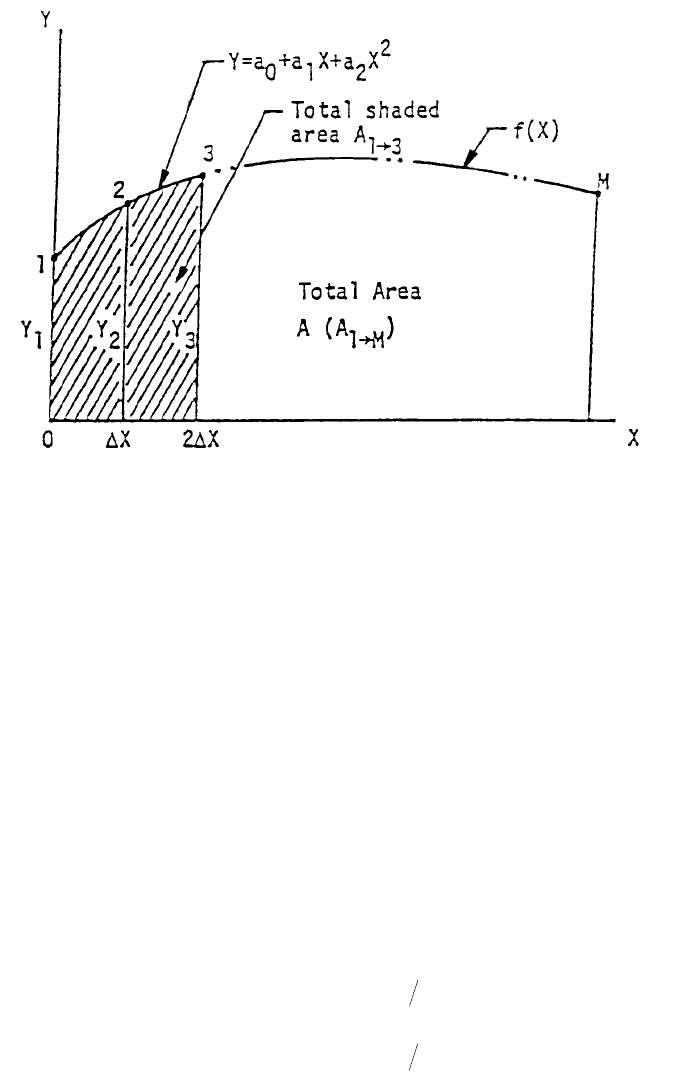
It is a quadratic equation describing a parabola. If we select Equation 20 to

approximate a segment of f(X) for numerical evaluation of the integral in Equation

8, three points are required on the f(X) curve as illustrated in Figure 4 in order to

determine the three coefﬁcients a

, a

, and a

. For simplicity in derivation, let the

three points be (0,Y

), (X,Y

), and (2X,Y

). Upon substitution into Equation 20,

we obtain:

(21)

(22)

and

(23)

As a

is already determined in Equation 21, it can be eliminated from

Equations 22 and 23 to yield:

(24)

and

(25)

FIGURE 4. Three points are required on the f(X) in order to determine the three coefﬁcients

, a

, and a

aXaXa Y

()

=∆∆

aXaXaY

22+

()

=∆∆

aXaYYX

1221

()

=−

()

∆∆

aXaYYX

1231

22+

()

=−

()

∆∆

The solutions of the above equations can be obtained by application of Cramer’s

Rule as:

(26)

and

(27)

Having derived a

, a

, and a

in terms of the ordinates Y

, Y

, and Y

, and the

increment in X, X, we are ready to substitute Equations 20, 21, 26, and 27 into

Equation 8 to compute the area A

1ø3

in Figure 4 under the parabola. That is:

After simpliﬁcation, it can be shown that the area

1ø3

is related to the ordinates

, Y

, and Y

, and the increment X by the equation:

(28)

When the above-described procedure is applied for numerical integration by

approximating the curve of the integrand Y(X) as a series of connected parabolas,

we can expand Equation 28 to cover the limits of integration to obtain:

(29)

Notice that the limits of integration are treated by having M stations which must

be an odd integer, and the stepsize X = (X

-X

)/(M–1). These stations are divided

into groups of three stations. Equation 28 has been successively employed for

evaluating the adjacent areas A

1ø3

, A

3ø5

, …, A

M–2øM

in order to arrive at Equation 29.

Equation 29 can also be written in the form of:

(30)

aYYXYYXYYYX

121 31 123

22342=−

()

−−

()

=− + −

()

∆∆ ∆

aYYXaXYYY X

221 1 123

22=−

()

−

[]

=− +

()

∆∆ ∆

AaXdX

→













∑

∫

∑

∆

YYY

13 1 2 3

→

=++

()

∆

YYY

odd

iii

odd

== ++

()

→+

−

()

−

∑∑

()

∆

YYYY

even

odd

=+++













()

−

()

−

∑∑

∆

which is the well-known Simpson’s rule. Program NuIntGra has the option of using

Simpson’s rule for numerical integration. It can be shown that when this program is

applied for the integration of the semi-circular area under the curve Y(X) = (1–X

)

the Simpson’s rule using different M stations will result in

Presented below are the program listings of NuIntGra in both QuickBASIC

and FORTRAN versions.

QUICKBASIC VERSION

M21416181101

Area 1.564 1.568 1.569 1.570 1.570

Error 0.45% 0.19% 0.13% 0.05% 0.05%