Pao Y.C. Engineering Analysis: Interactive Methods and Programs with FORTRAN, QuickBASIC, MATLAB, and Mathematica

Подождите немного. Документ загружается.

Sample Application

Using the input data and difference table as for the QuickBASIC version, the

interactive application of the FORTRAN version gives a sample run as follows:

MATLAB APPLICATION

A ﬁle DiffTabl.m can be created and added to MATLAB m ﬁles for printing

out the difference table. This ﬁle may be written as:

This m ﬁle then can be applied as illustrated by the following examples:

The statement format compact requests the results to be displayed without

unnecessary line spaces on screen.

It is appropriate at this time to demonstrate how some graphic capability of

MATLAB can be effectively utilized here in connection with the difference table.

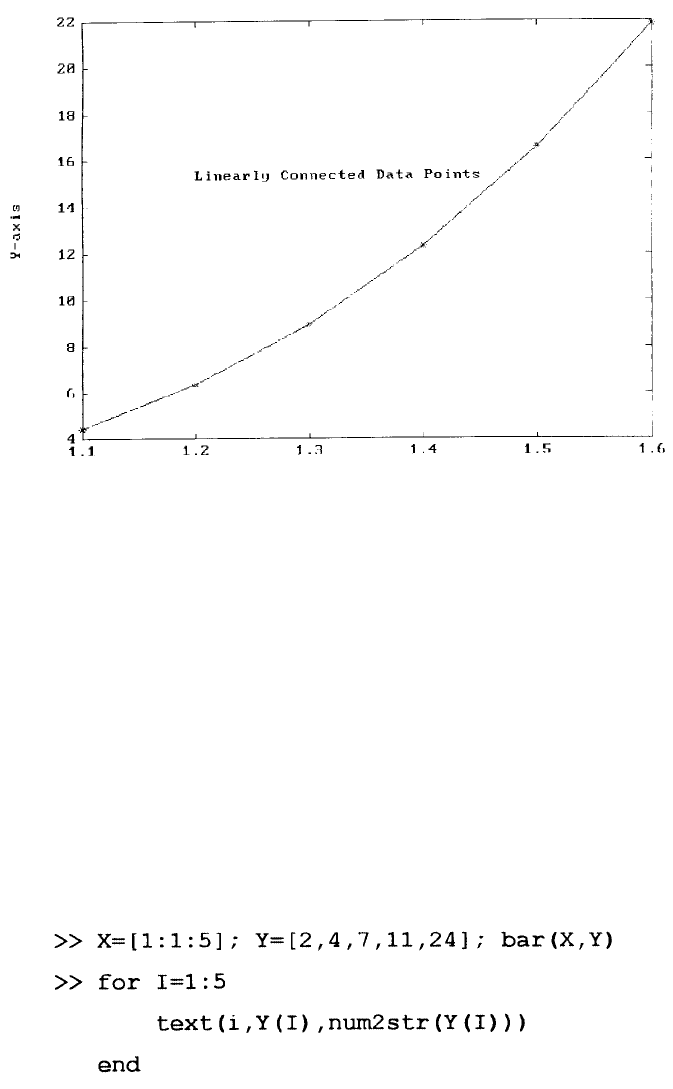
First, the calculation of the ﬁrst derivatives can be graphically interpreted as the

slope of the linear segments connecting the given points as shown in Figure 1 which

is obtained with the following interactively entered statements:

The ﬁrst, X = , statement creates an array having 6 elements whose values start

at 1.1 and ends at 1.6 and have a uniform increment of 0.1. In the plot statement,

the character — inside the ﬁrst set of single quotation signs requests that the given

set of points speciﬁed by the coordinates arrays X and Y are to be connected by

solid lines while the character * inside the second set of single quotation signs is

for marking those points.

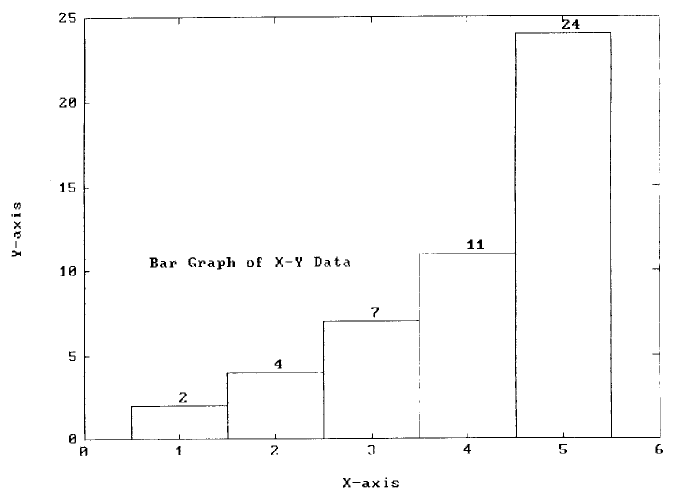
It also is appropriate at this time to introduce the bar graph feature of MATLAB

when we consider data set and difference table. Figure 2 is presented to show the

use of bar and num2str commands of MATLAB. The bar command plots a series

of vertical bars based on a set of coordinates arrays X and Y where X values must

be equally spaced. The num2str command converts a numerical value into a string,

it often facilitates the display of numerical values in conjunction with the text

command. The following interactively entered statements have enabled Figure 2 to

be displayed:

FIGURE 1. The calculation of the ﬁrst derivatives can be graphically interpreted as the slope

of the linear segments connecting the given points.

Notice that the ﬁrst two arguments for text are where the text string should be

placed whereas the third argument converts the value of Y(I) to be printed as a string.

The for-end loop allows all Y values to be placed at proper heights.

MATHEMATICA APPLICATIONS

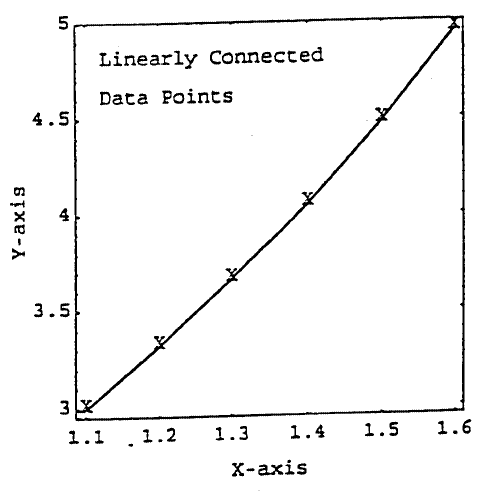
To produce a plot similar to Figure 3 in the program DiffTabl by application of

Mathematica, we may enter statements and obtain the following:

Input[1]: = X = Table[i,{i,1.1,1.6,0.1}; Y = Exp[X];

Input[2]: = g1 = Show[Graphics[Line[Table[{X[[i]],Y[[i]]},{i,1,6}]]]]

Input[3]: = g2 = Show[g1, Frame->True, AspectRatio->1,

FrameLabel->{“X-axis”,”Y-axis”}]

Input[4]: = g3 = Show[g2,Graphics[Table[Text[“X”,{X[[i]],Y[[i]]},

{i,1,16}]]

Input[5]: = Show[g3,Graphics[Text[“Linearly Connected”,{1.12,4.8},

{–1,0}],Text[“Data Points”,{1.12,4.6},{–1,0}]]]

FIGURE 2.

Only the ﬁnal plot is presented here. The intermediate plots designated as g1,

g2, and g3 can be recalled and displayed if necessary. The Line command in Input[3]

directs the speciﬁed pairs of coordinates to be linearly connected.

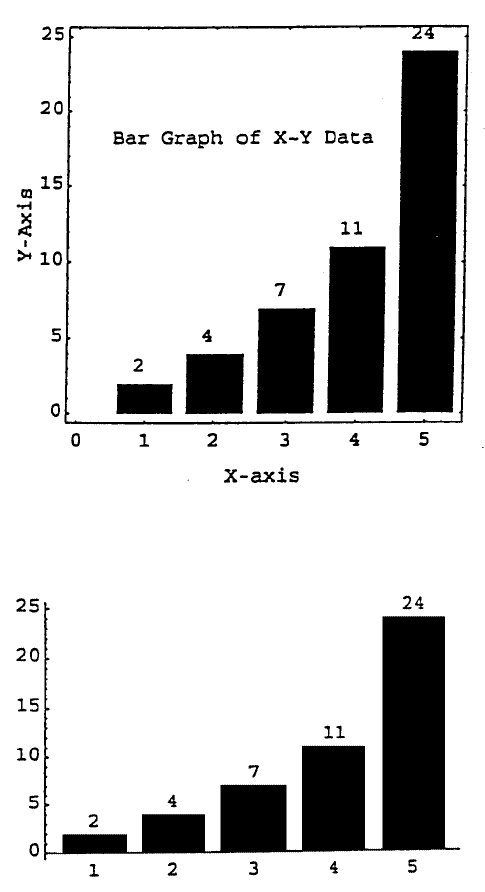
A bar graph can be drawn by application of Mathematica command Rectangle

and their respective values by the command Text. The following statements recreate

Figure 4 in the program DiffTabl.:

Input[1]: = X = {1,2,3,4,5}; Y = {2,4,7,11,24};

Input[2]: = g1 = Show[Graphics[Table[Rectangle[{X[[i]]–0.4,0},

X[[i]] + 0.4,Y[[i]]}],{i,1,5}]]]

Input[3]: = g2 = Show[g1,Graphics[Table[Text[Y[[i]],

{X[[i]]–0.1,Y[[i]] + 1}],{i,1,5}]]]

Input[4]: = g3 = Show[g2, Frame->True, AspectRatio->1]

Input[5]: = g4 = Show[g3,Graphics[Text[“Bar Graph of X–Y Data”,

{0.5,18},{–1,0}]]]

Input[6]: = Show[%,FrameLabel->{“X-axis”,”Y-axis”}]

FIGURE 3.

Notice that when no expression inside a pair of doubt quotes is provided for

the command Text, the value of the speciﬁed variable will be printed at the desired

location. This is demonstrated in Input[3].

Mathematica also has a function called BarChart in its Graphics package

which can be applied to plot Figure 5 as follows (again, some intermediate Output

responses are omitted):

FIGURE 4.

FIGURE 5.

Input[1]: = Y = {2,4,7,11,24};

Input[2]: = <<Graphics`Graphics`

Input[3]: = g1 = BarChart[Y]

Input[4]: = g2 = Show[g1,Graphics[Table[Text[Y[[i]],

{i,Y[[i]] + 1}],{i,1,5}]]

To print out a difference table of a given set of n y values, we can arrange the

y values and up to the n-1st order of their differences in a matrix form. The y values

are to be listed in the ﬁrst column and their ith-order diferences are to be listed in

the i + 1st column for i = 1,2,…,n–1. The following Mathematica input and ouput

statements demonstrate the print out of a set of 6 y values:

Input[1]: = y = {1,3,7,12,44,78};

Input[2]: = n = Length[y]; yanddys = Table[x,{i,n},{j,n}];

MatrixForm[yanddys]

Output[2] =

xxxxxx

Input[3]: = Do[yanddys[[i,1]] = y[[i]]; MatrixForm[yanddys]

Output[3] =

1 xxxxx

3 xxxxx

7 xxxxx

12xxxxx

44xxxxx

78xxxxx

Input[4]: = Do[Do[yanddys[[i,j]] = yanddys[[i + 1,j–1]]-yanddys[[i,j–1],

{i,n-j + 1}],{j,2,n}]; MatrixForm[yanddys]

Output[4] =

122–127–78

34126–51x

7527–25xx

12 32 2 x x x

44 34 x x x x

78xx xxx

Notice that in Input[2], the Mathematica functions Length has been applied

to determine the number of components in the array y, Table is used to initialize a

matrix of n by n with the character x, and MatrixForm allows the matrix, yanddys,

to be printed in a matrix form. Input[3] stores the y array into the ﬁrst column of

the matrix yanddys by application of the Mathematica command Do. Such looping

is extended in Input[4] where the higher order differences are generated by using

an inner index i and an outer index j. The column number j of the matrix yanddys

is increased from 2 to n but the length of each column is continuously decreased to

n-j + 1. Such DoDo arrangement is made possible by keeping the y values and their

differences in a column-by-column form.

4.3 PROGRAM LAGRANGI — APPLICATIONS OF LAGRANGIAN

INTERPOLATION FORMULA

Program LagrangI is designed to curve-ﬁt a given set of n points, (x

) for i = 1,

2,…,n, by a polynomial of n-1st degree based on the Lagrangian Interpolation

Formula:

(1)

If only the value of the function f(x) at a speciﬁed value of x = x

is needed,

then Equation 1 can be applied to compute

(2)

In Equations 1 and 2, the symbol  is to represent a product of a speciﬁed

number of factors such as:

(3)

Equation 1 can be proven if we write the equation which ﬁts the n given points

) for i = 1 to n by a combination of n functions L

1 to n

(x) as:

(4)

Notice that the ordinates f

1 to n

are utilized in Equation 4. We expect the functions

1 to n

(x) to behave in such a way that when x = x

only the f

(x) term in Equation

4 will contribute to f(x). That is to say when x = x

, L

) should be equal to unity

and the other L(x) should be equal to zero. Mathematically, we write demand that:

fx f x x x x

kik

()

=−

()

−

()

[]





















≠

∑

∏

fx f x x x x

kik

()

=−

()

−

()

[]





















≠

∑

∏

FFFF

∏

=…

fx fL x fL x fL x

()

+…+

()

11 2 2

(5)

The second condition of Equation 5 suggests that x-x

are factors of L

(x) for

k = 1,2,…,n but not x-x

. Therefore, we may write:

(6)

The constant associated with L

(x), c

is to be determined by satisfying the ﬁrst

condition of Equation 5. That is:

(7)

Consequently, the complete expression for L

(x) is:

(8)

And, when Equation 8 is substituted into Equation 4, we arrive at Equation 1.

A numerical example will clarify the application of Equation 2. Consider the

case of three given points (x

) = (1,2), (x

) = (1.5,2.5), (x

) = (3,4), then n =

3. If we need to calculate f(x = 2), Equation 2 can be used to ﬁnd the equation which

passes all three points. That is:

L x and L x for j i

ii ji

()

=≠10

Lx cx x x x x x x x x x

ii i i

()

=−

()

−

()

…−

()

−

()

…−

()

−+

cxx

iik

=−

()













≠

∏

Lx x x x

ikix

()

=−

()

[]

−

≠

∏

xx xx

xxxx

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

1213

2123

3132

15 3

11513

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

=− +

()

−−+

()

+−+

()

xx xx x x

15 1 15 3

115

31315

24545

25 15

.. ..

When x = 2, f(x = 2) = 3. Actually, the value of f(x = 2) can be speciﬁcally

calculated as:

QUICKBASIC VERSION

xx xx

xxxx

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

(

21523

11513

1213

2123

3132

))

−

()

−

()

−

()

−

()

−

()

−

()

−

()

−

()

=− + + =

2123

15 1 15 3

21215

31315