Pao Y.C. Engineering Analysis: Interactive Methods and Programs with FORTRAN, QuickBASIC, MATLAB, and Mathematica

Подождите немного. Документ загружается.

Sample Application

The interactive question-and-answer process in solving the polynomial 4x

+ 2x + 1 = 0 using the Newton-Raphson method and the subsequent display on

screen of the iteration goes as follows:

Notice that in the

FORTRAN

program

FindRoot

, the

statement functions

F(X)

and FP(X) are deﬁned for calculating the values of the given function and its

derivative at a speciﬁed X value. Also, a

character variable

AS is declared through

a CHARACTER*N with N being equal to 1 in this case when AS can have only

one character as opposed to the general case of having N characters.

MATLAB A

PPLICATION

FindRoot.m

ﬁle can be created and added to

MATLAB

m ﬁles for the purpose

of ﬁnding a root of a polynomial or transcendental equation. In this ﬁle, the four

methods discussed in the

FORTRAN

QuickBASIC

versions can all be incorpo-

rated. Since some methods require that the left and right bounds, x

and x

, be

provided, the m ﬁle listed below includes as arguments these bounds along with the

tolerance and the limited number of iterations:

Notice that the equation for which a root is to be found should be deﬁned in a

mile ﬁle called

FofX.m

, and that if the Newton-Raphson method, i.e., option 4, is

to be used, then the ﬁrst derivative of this equation should also be deﬁned in a m

ﬁle called

DFDX.m

. We next present four examples demonstrating when all four

methods are employed for solving a root of the polynomial F(x) = 4x

+ 3x

+ 2x

+ 1 = 0 between the bounds x = –1 and x = 0 using a tolerance of 10

–5

. In addition

FindRoot.m

ﬁle, two supporting m ﬁles for this case are:

The four sample solutions are (some printout have been shortened for saving

spaces:

Notice that incremental search, half-interval search, interpolation, and Newton-

Raphson methods take 28, 17, 16, and 4 iterations to arrive at the root x = –0.6058,

respectively. The last method therefore is the best, but is only for this polynomial

and not necessary so for a general case.

Method of Successive Substitution

As a closing remark, another method called successive substitution is sometimes

a simple way of ﬁnding a root of a transcendental equation, such as for solving the

angle in a four-bar linkage problem shown in Figure 1. Knowing the lengths L

amd L

, and the angle of the driving link AB, the angle of the driven link CD,

can be found by guessing an initial value of

(0)

and then continuously upgraded

using the equation:

(5)

where the superscript k serves as an iteration counter set equal to zero initially. For

changing from 0 to 360°, it is often required in study of such mechanism to ﬁnd

the change in

. This is left as a homework for the reader to exercise.

γααγ

AB CD

()

−

()

=−+−

()

[]













cos cos cos

ATHEMATICA

PPLICATIONS

To illustrate how Mathematica can be applied to ﬁnd a root of F(x) = 1 + 2x

+ 3x

+ 4x

= 0 in the interval x = [xl,xr] = [–1,0], the linear interpolation is used

below but similar arrangements could be made when the incremental, or, bisection

search, or, Newton-Raphson method is selected instead.

Input[1]: = F[x_]: = 1. + 2*x + 3*x^2 + 4*x^3

Input[2]: = xl = –1; xr = 0; ﬂ = F[xl]; fr = F[xr]; fx = ﬂ;

Input[3]: = Print[“xl = “,xl,” xr = “,xr,” F(xl) = “,ﬂ,” F(xr) = “,fr]

Output[3]: = xl = –1 xr = 0 F(xl) = –2. F(xr) = 1.

Input[4]: = (While[Abs[fx]>0.00001, x = (xr*ﬂ-xl*fr)/(ﬂ-fr);fx = F[x];

Print[“x = “,N[x,5],” F(x) = “,N[fx,5]];

If[fx*fl<0, xr = x;fr = fx;, xl = x;fl = fx;]])

Output[4]: = x = –0.33333 F(x) = 0.51852

x = –0.47059 F(x) = 0.30633

x = –0.54091 F(x) = 0.1629

x = –0.57548 F(x) = 0.080224

x = –0.59185 F(x) = 0.037883

x = –0.59944 F(x) = 0.017521

x = –0.60292 F(x) = 0.0080245

x = –0.60451 F(x) = 0.0036586

FIGURE 1. Successive substitution sometimes is a simple way of ﬁnding a root of a tran-

scendental equation, such as for solving the angle γ in a four-bar linkage problem.

x = –0.60523 F(x) = 0.0016646

x = –0.60556 F(x) = 0.00075666

x = –0.60571 F(x) = 0.00034379

x = –0.60577 F(x) = 0.00015618

x = –0.60580 F(x) = 0.000070940

x = –0.60582 F(x) = 0.000032222

x = –0.60582 F(x) = 0.000014635

x = –0.60583 F(x) = 6.6473x10

–6

Notice that 16 iterations are required to achieve the accuracy that the value of

|F(x)| should be no greater than 0.00001. In Input[1], the equation being solved is

deﬁned in F[x]. 1. is entered instead of an integer 1 so that all computed F(x) values

when printed will be in decimal form instead of in fractional form as indicated in

Output[3]. In Input[4], a pair of parentheses are added to allow long statements be

entered using many lines and broken and listed with better clarity. Also, N[exp,n]

is applied to request that the value of expression, exp, be handled with n signiﬁcant

ﬁgures. The command If is also employed in Input[4]. It should be used in the form

of If[condition, GS1, GS2], which implements the statements in the group GS1 or

in the group GS2 when the condition is true or false, respectively. Abs computes

the absolute value of an expression speciﬁed inside the pair of brackets.

3.3 PROGRAM NEWRAPHG — GENERALIZED

NEWTON-RAPHSON ITERATIVE METHOD

Newton-Raphson method

has been discussed in the program FindRoot in iterative

solution of polynomials and transcendental equation. Here, for an extended discus-

sion of this method for solving a set of speciﬁed equation, we reintroduce this method

in greater detail. This method is based on Taylor’s series.

Let us start again with

the case of one equation of one variable. Let F(X) = 0 be the equation for which a

root X

is to be found. If this root is known to be in the neighborhood of X

, then

based on Taylor’s series expansion we may write:

(1)

where:

(2)

and the prime in Equation 1 represents differentiation with respect to X. Since X

is a root of F(X) = 0, therefore F(X

) = 0. And if X

is sufﬁciently close to X

, X

is small and the terms involving (X)

and higher powers of X in Equation 1 can

be neglected. It leads to:

(3)

FX FX F X X F X X

rg g g

()

′

()

′′

()

+…∆∆

∆XX X

=−

XX FXFX

rg g g

=−

()

′

()

[]

This result suggests that if we use a projected root value according to Equation 3

as next guess, an iterative process can then be continued until the condition F(X

) =

0 is, if not exactly, almost satisﬁed.

The Newton-Raphson iterative procedure is developed on the above mentioned

concept by using the formula:

(4)

where k is an iteration counter. By providing an initial guess, X

(0)

, Equation 4 is to

be repeatedly applied until F(X

(k)

) is almost equal to zero which by using a tolearance

can be tested with the condition:

(5)

As an example, consider the case of:

(6)

for which

(7)

If we make an initial guess of X

(0))

= 1.75 and set a tolerance of = 0.00001, the

Newton-Raphson iteration will proceed as follows:

Program FindRoot has a fourth option for Newton-Raphson iteration of a root

for a speciﬁed equation of one variable. The results tabulated above are obtained by

the program FindRoot.

TRANSCENDENTAL EQUATIONS

Not only for polynomials, Newton-Raphson iterative method can also be applied

for ﬁnding roots of transcendental equations. To introduce a transcendental equation,

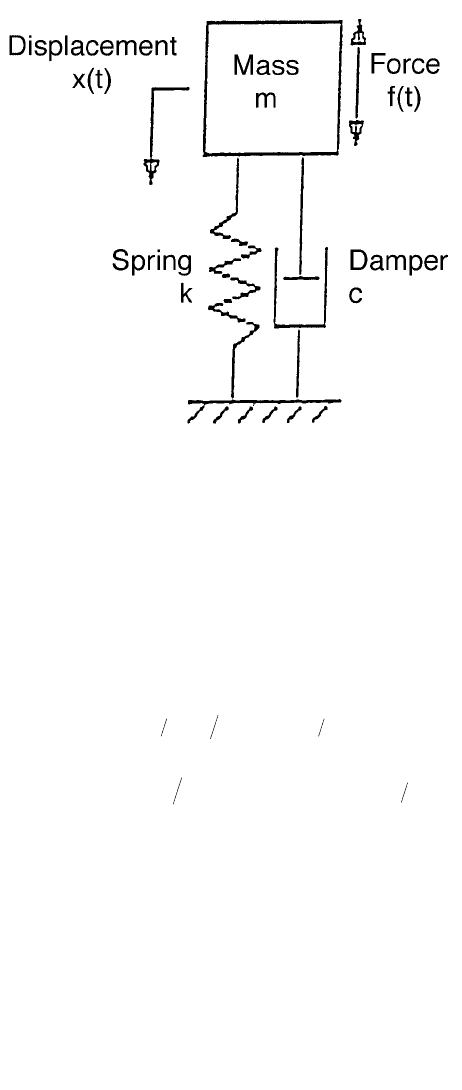
let us consider the problem of a moving vehicle which is schematically represented

by a mass m in Figure 2. The leaf-spring and shock absorber are modelled by k and

c, respectively.

Trial No. X F(X)

0 1.7500 0.23438

1 2.0572 –0.05701

2 1.9825 0.01753

3 2.0008 –0.00085

4 2.0001 –0.00011

5 2.0000 0.00001

XXFXFX

( ) () () ()

=−

()

′

()

k()

()

<ε

FX X X X

()

=− + −=

61160

′

()

=−+FX X X31211

If the vehicle is suddenly disturbed by a lift or drop of one of its supporting

boundaries by one unit (mathematically, that is a unit-step disturbance), it can be

shown

that the elevation change in time of the mass, here designated as X(t), is

described by the equation:

(8)

where:

(9,10)

(11,12)

Equation 8 is a transcendental equation.

In actual design of a vehicle, it is necessary to know the lengths of time that are

required for the vehicle to respond to the unit-step disturbance and reaching to the

amounts equal to 10, 50, and 90 percent of the disturbance. Such calculations are

needed to ascertain the delay time, rise time, and other items among the design

speciﬁcations shown in Figure 3. If one wants to know when the vehicle will rise

up to 50 percent of a unit-step disturbance, then it is a problem of ﬁnding a root,

t = t

, which satisﬁes the equation:

FIGURE 2. Mechanical vibration system with one degree-of-freedom.

X t a Exp a t a t a

()

=− −

()

1234

sin

akma acm

()

′

akmc m a aa

42=−

()

−.

, tanand

X t a Exp a t a t a

rrr

()

=− −

()

=105

12 34

sin .

Or, the problem can be mathematically stated as solving for t

from the following

transcendental equation by knowing the constants a

1–4

As an example, let a

= 1, a

= 0.2 sec

–1

, a

= 1 sec

–1

, and a

= 1.37 radian then

the transcendental equation is:

(13)

To ﬁnd a root t

for Equation 3, we select an initial guess t

(0)

= 0.5 and apply

the fourth option of the program FindRoot. The results are listed below. It indicates

that the mass reaches 50% of the unit-step disturbance in approximately 1.1 seconds.

FIGURE 3. Design speciﬁcations in time domain: overshoot x

, delay time t

, rise time t

and settlement time t

a Exp a t a t a

1234

05 0−

()

−=sin .

t−

()

−=

sin . .

137 05 0

An associated problem of the mechanical vibration problem is to ﬁnd the mag-

nitude and time of overshoot when the mass reaches the farthest point as illustrated

in Figure 1. Instead of Equation 13, for calculation of overshoot we examine the

equation:

(14)

To determine the maximum of X(t), we differentiate Equation 14 with respect

to t to derive the expression for the ﬁrst derivative of X(t). That is:

(15)

The magnitude and time of maximum X(t) can then be determined by setting

Equation 15 equal to zero. In so doing, the fourth option of the program FindRoot

is again applied using the bounds t

= 1 and t

= 2 to ﬁnd that X

max

is equal to 1.523

or overshoot is equal to 53% and occurs at t = 3.145 seconds. See Figure 2 for

deﬁnitions of these design speciﬁcations.

EXTENDED NEWTON-RAPHSON METHOD

The iterative method of Newton-Raphson for solving a either polynomial or

transcendental equation of one variable can be extended into solution of multiple

equations of multiple variables. Consider the case of two equations of two variables,

u(x,y) = 0 and v(x,y) = 0. Let (x

) be a guessing solution of these two equations.

In that neighborhood, the Taylor’s series for f(x,y) and g(x,y) are:

(16)

and

(17)

where u

,

∂u/∂x and v

∂v/∂y, and the root location (x

) is predicted using the

adjustments x and y. That is,

(18,19)

Since it is hoped that u(x

) and v(x

) would both be equal to zero,

Equations 16 and 17 therefore can be expressed, after dropping the higher order

terms of x and y, in the forms of:

(20)

and

(21)

Xt e t

()

=− +

()

−

1137

sin .

dX t dt e t t

()

−+

()

[]

−.

. sin . cos .

2 1 37 1 37

uxy uxy uxyxuxyy

rr gg xgg ygg

,, , ,

()

+…∆∆

vxy vxy vxyxvxyy

rr gg xgg ygg

,, , ,

()

+…∆∆

xx x yy y

rg rg

=+ =+∆∆ and

uxyxuxyy uxy

xgg ygg gg,,

,, ,

()

=−

()

∆∆

vxyxvxyy vxy

xgg ygg gg,,

,, ,

()

=−

()

∆∆