Pao Y.C. Engineering Analysis: Interactive Methods and Programs with FORTRAN, QuickBASIC, MATLAB, and Mathematica

Подождите немного. Документ загружается.

4. Given eight data points (X

) for i = 1,2,…,8 as listed, ﬁt them by the

least-squares method with the equation Y = a

+ a

X + a

. Find a

1–3

applying the computer program LeastSqG.

5. A set of three points are provided as listed: (1,0.2), (2,0.5), and (3,0.6).

These points are to be ﬁtted by application of the least-squares method

using a linear combination of (a) two functions x and x

, or (b) two other

functions x

and x

. Which ﬁt will be better, a or b? Back up your answer

with detailed calculations.

6. Given three points (1,2), (3,5), and (4,13), two selected functions f

(x) =

x–1 and f

(x) = x

are to be linearly combined to ﬁt these points by the

equation y = a

(x) + a

(x) = a

(x–1) + a

. Derive two equations

needed for solving a

and a

by use of the Least-Squares method.

7. Given 7 points of which the coordinates are X(i) and Y(i) for i = 1 to 7,

a least-squares ﬁt of these points with a linear combination of 3 selected

functions f

(X) = X, f

(X) = sin2X, and f

(X) = e

-X

in the form of Y(X) =

C(1)f

(X) + C(2)f

(X) + C(3)f

(X) has been conducted and the coefﬁcients

C(1) to C(3) have been found. Complete the following segment of FOR-

TRAN program to calculate the total error E which is the sum of the

squares of the differences between Y(X(i)) and Y(i) for i = 1 to 7.

DIMENSION X(7),Y(7),C(3)

DATA X,Y,C/(17 real numbers separated by,)/

insert statements for

< - - - calculation of E involving

C, X, Y, and f

, f

, and f

WRITE (*,*) E

STOP

END

8. For a given set of data (1,–2), (2,0), (3,1), and (4,3), two equations have

been suggested to ﬁt these points. They are Y = X–2 and Y = (-X

7X–10)/2. Based on the least-squares criterion, which equation should be

chosen to provide a better ﬁt? Explain why.

9. Given 12 points of which the coordinates are X(i) and Y(i) for i = 1 to 7,

a least-squares ﬁt of these points with a linear combination of 4 selected

functions f

(X) = X, f

(X) = sin2X, f

(X) = cos3X, and f

(X) = e

-X

in the

form of Y(X) = C(1)f

(X) + C(2)f

(X) + C(3)f

(X) + C(4)f

(X) has been

conducted and the coefﬁcients C(1) to C(4) have been found. Complete

the following segment of FORTRAN program to calculate the total error

E which is the sum of the squares of the differences between Y(X(i)) and

Y(i) for i = 1 to 12, using a FUNCTION subprogram F(I,X) which evaluate

the Ith selected function at a speciﬁed X value for i = 1 to 4.

X12345678

Y 1.13 1.45 1.76 2.19 2.43 2.79 3.51 4.88

DIMENSION X(12),Y(12),C(4)

DATA X,Y,C/(28 real numbers separated by,)/

insert statements for

< - - - calculation of E involving

C, X, Y, and f

, f

, and f

WRITE (*,*) E

STOP

END

10. Any way one can solve the above-listed problem by application of MAT-

LAB? Compare the computed results obtained by QuickBASIC, FOR-

TRAN, and MATLAB approaches.

11. Try Mathematica and compare results for the above problems.

CUBIC SPLINE

1. Presently, program CubeSpln is not interactive. Expand its capability to

allow interactive input of the number of points, N, and coordinates (X

)

for i = 1 to N. Also, user should be able to specify the KK value so that

both periodic or nonperiodic data points can be ﬁtted. Call this program

CubeSpln.X and rerun the case used in Sample Application.

2. Change the program CubeSpln slightly to allow a sixth point to be con-

sidered. Add a sixth point whose Y value is equal to that of the ﬁrst point

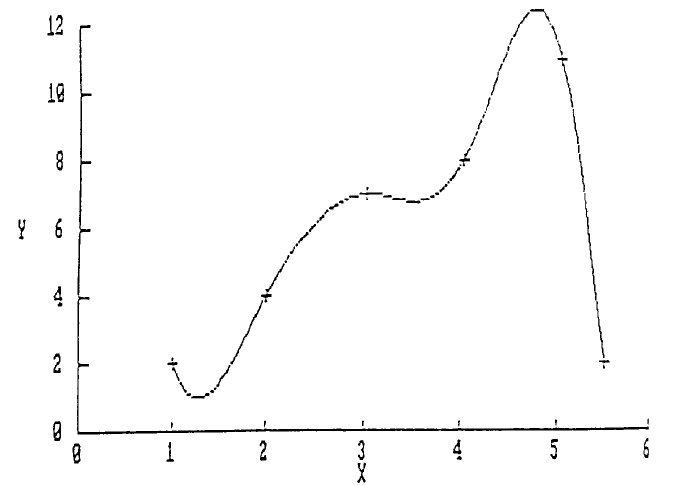
then run it as a periodic case by changing KK equal to 2. The resulting

plot for X(6) = 5.5 should be as shown below.

3. Use the program CubeSpln.X to run Problem 2.

4. Apply spline.m of MATLAB to ﬁt the points (1,2), (2,4), (3,7), and (4,13)

and then plot the curve by using plot.m. Mark the points by the character *.

5. Apply spline.m of MATLAB to ﬁt the points (0.5,3), (1.2,6), (2.5,5), and

(3.7,11) and then plot the curve by using plot.m. Mark the points by the

character + .

6. Apply spline.m of MATLAB to ﬁt the points (3,3), (3.6,6), (4.2,8), and

(5.1,11) and then plot the curve by using plot.m.

7. Combine the curves obtained in Problems 4 to 6 into a composite graph

by using solid, broken, and center lines which in use of plot.m require to

specify with ‘-’, ‘- - -’, and ‘-.’, respectively. The resulting composite

graph should look like the ﬁgure below.

8. Use text command of MATLAB to add texts ‘Problem 4’, ‘Problem 5’,

and ‘Problem 6’ near the respective curves already drawn in Problem 7.

9. The temperature data in

°F, collected during a period of seven days are (2,75),

(3,80), (4,86), (5,92), (6,81), and (7,90). Cubic-spline ﬁt these data, plot the

curve, and label the horizontal axis with ‘Days’ and vertical axis with ‘Tem-

perature, in Fahrenheit’ by use of xlabel and ylabel commands of MATLAB.

10. Add to the graph obtained for Problem 9 by marking the data points with

the character * and also a text ‘Cubic Spline of Temperature Data’ at an

appropriate location not touching the spline curve.

2.7 REFERENCES

1. Y. C. Pao, “On Development of Engineering Animation Software,” in Computers in

Engineering, K. Ishii, editor, ASME Publications, New York, 1994, pp. 851–855.

2. A. Ralston, A First Course in Numerical Analysis, McGraw-Hill, New York, 1965.

3. H. Flanders, R. R. Korfhage, and J. J. Price, A First Course in Calculus with Analytic

Geometry, Academic Press, New York, 1973.

Roots of Polynomials and

Transcendental Equations

3.1 INTRODUCTION

In the preceding chapter, we derive equations which ﬁt a given of data either exactly,

or, by using a criterion such as the least-squares method. Once such equations have

been obtained in the form of y = C(x) when the data are two-dimensional, or, z =

S(x,y) when the data are three-dimensional. It is next of common interest to ﬁnd

where the curve C(x) intercepts the x-axis, or, where the surface S(x,y) intercepts

with the x-y plane. Mathematically, these are the problems of ﬁnding the

roots

the equations C(x) = 0 and S(x,y) = 0, respectively. The equation to be solved could

be a

polynomial

of the form P(x) = a

+ a

x + … + a

i–1

+ … + a

N + 1

which is

of Nth order, or, a

transcendental equation

such as C(x) = a

sinx + a

sin2x + a

sin3x.

As it is well known, a polynomial of Nth order should have N roots which could

be real, or, complex conjugate pair if the coefﬁcients of the polynomial are all real.

Geometrically speaking, only those real roots really pass the x-axis. For a transcen-

dental equation, there may be inﬁnite many roots. In this chapter, we shall introduce

computational methods for ﬁnding the roots of polynomials and transcendental

equations. Beginning with the very primitive approach of incremental and half-

interval searches, the approximate location of a particular root is to be located. More

reﬁned, systematic methods such as the linear interpolation and Newton-Raphson

methods are then followed to determine the more precise location of the root. A

program called

FindRoot

incorporating the four methods is to be presented for

interactive solution of a particular root of a given polynomial or transcendental

equation when the upper and lower bounds of the root are provided.

Also discussed is a method called

Successive Substitution

. A transcendental

equation derived from analysis of a four-bar linkage problem is used to demonstrate

how roots are to be found by application of this method. Another transcendental

equation has been derived for the unit-step response analysis of a mechanical vibra-

tion system and its roots solved by application of the Newton-Raphson method to

illustrate how the design speciﬁcations are checked in the time domain.

Since the Newton-Raphson method for solving F(x) = 0 which can be a poly-

nomial, or, transcendental equation of one variable is based on the Taylor’s series

involving the derivatives of F(x), it can be extended to the solution of two-equations

(x,y) = 0 and F

(x,y) = 0 by application of Taylor’s series involving partial deriv-

atives of both F

and F

with respect to x and y. A program called

NewRaphG

has

been developed for this purpose. Also, this generalized Newton-Raphson method

allows the quadratic factors of a higher order polynomial to be iteratively and contin-

uously extracted and their quadratic roots solved by the so-called

Bairstow

method.

For that, a program called Bairstow is made available for interactive application.

Both

QuickBASIC

and

FORTRAN

versions for the above-mentioned programs

are presented. Both the application of the

roots

m-ﬁle of

MATLAB

in place of the

program Bairstow and direct conversion of the program

FindRoot

into

MATLAB

version are also presented. The

Mathematica

’s function

NSolve

is introduced in

place of the program

Bairstow

if the user prefers. Also the linear interpolation

method used in the program

FindRoot

has been translated into

Mathematica

version. In fact.

Mathematica

has its own

FindRoot

based on the Newton-Raphson

method.

3.2 ITERATIVE METHODS AND PROGRAM FINDROOT

Program FindRoot is developed for interactive selection of an iterative method

among the four made available: (1) Incremental Search, (2) Bisection Search, (3)

Linear Interpolation, and (4) Newton-Raphson Iteration. Polynomials are often

encountered in engineering analyses such as the characteristic equations in vibra-

tional and buckling problems. The roots of a polynomial are related to some impor-

tant physical properties of the systems being analyzed, such as the frequencies of

vibration or buckling loads. A nth degree polynomial can be expressed as:

(1)

For n = 1,2,3, there are formulas readily available in standard mathematical

handbooks

for ﬁnding the roots. But for large n values, computer methods are then

necessary to help ﬁnd the roots of a given polynomial. The methods to be discussed

here are simple and direct and are applicable to not only polynomials but also

transcendental equations such as 5 + 7cosx – cos60° – cos(60° – x) = 0 related to a

linkage design problem

or x = 40000/{1–0.35sec[40(x/10

)

0.5

]} arisen from buck-

ling study of slender rods.

NCREMENTAL

EARCH

For convenience of discussion, let us consider a cubic equation:

(2)

To ﬁnd a root of P(x), we ﬁrst observe that P(x = –

∞

)<0, P(x = 0) = 1, and P(x =

–

∞

)>0. This indicates that the P(x) curve must cross the x axis, possibly once or an

odd number of times. Also, the curve may remain above the x-axis or cross it an even

number of times. To further narrowing down the range on the x-axis, in which the root

is located, we can begin to check the sign of P(x) at x = –10 and search toward the

origin using an increment of x equal to 2. That is, we may construct a list such as:

Px a ax ax ax a x

()

=+ + +…+ +

−

∑

12 3

Px x x x

()

=+ + + =12 3 4 0

Since P(x) changes sign from x = –2 to x = 0, this incremental search can be

continued using an increment of x equal to 0.2 and the left bound x = –10 by replaced

by x = –2 to obtain:

The search continues as follows:

If only three signiﬁcant ﬁgures accuracy is required, then x = 0.606 is the root

and it has taken 23 incremental search steps to arrive at this answer. If better accuracy

is required, the root should then be sought between x = –0.6060 and x = –0.6058.

Program

FindRoot

prepared both is

QuickBASIC

and

FORTRAN

has one of

the options using the above-explained incremental search method, it also has other

methods of ﬁnding the roots of polynomials and transcendental equations to be

introduced next.

ISECTION

EARCH

The above example of incremental search shows that if we search from left to

right of the x-axis for the root of 4x

+ 3x

+ 2x + 1 = 0 between x = –2 and x = 0,

it would be longer than if we search from right to left because the root is near x =

0. Rather than using a ﬁxed incremental in the incremental search method, the

bisectional method uses the mid-point of the two bounds of x in search of the root.

It involves the testing of the signs of the polynomial at the bounds of the root and

replacing the bounds. The two search methods follow the same procedure. So, the

bisection method would go as follows:

X –10 –8 –6 –4 –2 0

P(x) – –––– +

X –1.8 –1.6 • • • –0.8 –0.6

P(x) – – – – +

x –0.78 –0.76 • • • –0.62 –0.60

P(x) ––––+

x –0.618 –0.616 • • • –0.606 –0.604

P(x) – – – – +

x –0.6058

P(x) +

x –10 0 –5 –2.5 –1.25 –0.625 –0.3125

P(x) – + – – – – +

x –0.46875 –0.546875 –0.5859375 –0.6054688

P(x) + + + +

If we require only three signiﬁcant ﬁgures accuracy, then –0.606 can be consid-

ered as the root after having taken 18 bisection search steps.

INEAR

NTERPOLATION

Notice that both the incremental and bisection search methods make no use of

the values of the polynomials at the guessed x values. For example, at x = –10 and

x = 1, the polynomial P(x) has values equal to –3719 and 1, respectively. Since P(x =

1) has a smaller value than P(x = –10), we would certainly expect the root to be

closer to x = 1 than to x = –10. The linear interpolation makes use of the values of

P(x) at the bounds and calculates a new guessing value of the root using the following

formulas derived from the relationship between two similar triangles:

(3)

where x

and x

are the left and right bounds of the root, which in this case are

equal to –10 and 1, respectively. Based on Equation 3 and P(x

) = –3719 and P(x

) =

1, we can have x = –0.002688 and P(x) = 0.9946. Since P(x)>0, we can therefore

replace x

= 1 with x

= 0.002688. Linear interpolation involves the continuous use

of Equation 3 and updating of the bounds.

EWTON

-R

APHSON

TERATIVE

ETHOD

Linear interpolation method uses the value of the function, for which the root

is being sought; Newton-Raphson method goes one step farther by involving with

the derivative of the function as well. For example, the polynomial P(x) = 4x

+ 3x

+ 2x + 1 = 0 has its ﬁrst-derivative expression P'(x) = 12x

+ 6x + 2. If we guess

the root of P(x) to be x = x

and P(x

) is not equal to zero, the adjustment of x

calling

∆

x, can be obtained by application of the Taylor’s series:

Since the intention is to ﬁnd an adjustment



x which should make P(x



equal to zero and

∆

x itself should be small enough to allow higher order of



x to

be dropped from the above expression. As a consequence, we can have 0 = P(x

) +

P'(x

)



x, or

(4)

x –0.6152344 –0.6103516 –0.6079102 –0.6066895

P(x) – – – –

x –0.6060792 –0.6057741 –0.6059266

P(x) – + -2.68817E-04

x x Px x x Px

LLR R

−

()

−

()

[]

=−

()()

Px x Px P x x P x x

ggg g

()

′

()

[]

′′

()

[]

()

…∆∆∆12

∆xPxPx

=−

()

′

()

Equation 4 is to be continuously used to make new guess, (x

)

new

= x



x, of

the root, until P(x = (x

)

new

) is negligibly small.

The major shortcoming of this method is that during the iteration, if the slope

at the guessing point becomes too small, Equation 4 may lead to a very large Dx

so that the x

may fall outside the known bounds of the root. However, this method

has the advantage of extending the iterative procedure to solving multiple equations

of multiple variables (see program

NewRaphG

An interactive program called

FindRoot

has been developed in both

QuickBA-

SIC

and

FORTRAN

languages with all four methods discussed above. User can

select any one of theses methods, edits the equation to be solved, speciﬁes the bounds

of the root, and gives the accuracy tolerance for termination of the root ﬁnding. The

programs are listed below along with sample applications.

UICK

BASIC V

ERSION

Sample Application

All four methods have been applied for searching the roots of the equation

–sin(x)–1 = 0 in the intervals (–1,–0.5) and (1,1.5). The negative root equal to

–0.63673 was found after 27, 15, 5, and 3 iterations and the positive root equal to 1.4096

after 29, 15, 4, and 4 iterations by the incremental search, bisection search, linear

interpolation, and Newton-Raphson methods, respectively. An accuracy tolerance of

1.E–5 was used for all cases. For solving this transcendental equation, Newton-

Raphson therefore is the best method.

FORTRAN V

ERSION