Панов В.К. Физические основы теплотехники. Ч. I: Термодинамика

Подождите немного. Документ загружается.

§ 11. Работа

поток, секундомер и отметим частицы газа, находящиеся во

входном сечении трубы. Затем включим все: и поток, и секун-

домер — для удобства на одну секунду. Отмеченные частицы

перейдут в некоторое сечение дальше по трубе, а их место

займут вновь прибывшие. То есть через входное и любое дру-

гое сечение трубы за секунду пройдет заштрихованный объем

газа. Это цилиндр, длина образующей которого равна скоро-

сти, поскольку время наблюдения — 1 с. Его объем:

W = S

w , м

м/с = м

/с.

Это объемный расход — объем газа, проходящий через

сечение потока за секунду. Определим теперь массу газа, на-

ходящегося в этом объеме:

М = ρ

W, (кг/м

) · (м

/с) = кг/с.

Это будет массовый расход. Остается определить плот-

ность газа, а ее, как упоминалось раньше, определяют из урав-

нения Клапейрона – Менделеева (2.8):

ρ = р/(RT).

Отсюда сразу видно, что плотность газа может быть лю-

бой в зависимости от значений параметров состояния. Тогда

М = Wp/(RT). (2.13)

Задача решена, поскольку в выражение (2.13) входят как

раз те величины, которые мы измеряем. Сейчас на производ-

стве уже используются расходомеры, которые объединяют в

одном приборе все показанные на рис. 2.5 датчики.

Итак, важнейшая производственная задача – измерение

расхода газа решена именно на основе уравнения Клапейрона–

Менделеева. Более того, (2.13) можно переписать в таком виде:

. (2.14)

Это уравнение состояния для потока идеального газа.

9.2. Диаграммы

Из того, что между параметрами состояния существует

связь (для газа она выражается уравнением Клапейрона–

Менделеева), вытекает возможность использования для ото-

бражения процессов термодинамических диаграмм состояния.

Впервые это сделал сам Клапейрон. Чтобы прояснить связь

между уравнением состояния и диаграммами, придется сде-

лать небольшое «лирическое отступление».

§ 11. Работа

Человек так устроен, что бóльшую часть сведений об окружающей

действительности получает через зрение. Однако орган зрения хоть и изу-

мительный по сложности инструмент, но весьма ограниченный по своим

возможностям. Из всего огромного спектра электромагнитных волн мы вос-

принимаем глазом как свет, несущий изображение, только тончайший диа-

пазон. Очень мелкие объекты, например клеточные структуры, мы не видим

без специальных приспособлений. Крупные объекты, которые невозможно

окинуть взглядом, по существу мы тоже не видим. Но и это не все. Очень

быстрые процессы, как и очень медленные, мы тоже не видим. Так уж уст-

роен наш основной поставщик информации, что в окружающем мире мы

способны видеть крайне мало.

Но благодаря разуму, способному мыслить образами, непосредст-

венно не наблюдаемыми, и делать выводы (додумывать) на основании кос-

венных данных, мы знаем гораздо больше, чем видим. Из-за этого появляется

множество разнообразных приемов, способов, условностей, позволяющих

создать наглядные геометрические образы, отражающие ненаблюдаемые объ-

екты. Так появляются, в частности, чертежи, схемы, модели процессов, полу-

ченные с помощью хитроумных приемов визуализации.

Например, когда выясняется, что между величиной Y и величиной Х

существует связь, то, выражая ее, мы пишем: Y = f (X). И даже в том случае,

если конкретный вид этой зависимости известен (ну хотя бы у = ax + b), хо-

чется все же ее увидеть. Ведь все-таки у = ax + b – это не образ, а последо-

вательность действий, позволяющих вычислить соответствующее значение Y,

когда выбрано какое-то значение Х.

Геометрические образы мы традиционно представляем себе состоя-

щими из точек. Так, последовательность друг за другом расположенных то-

чек образует линию, перемещением линии можно получить поверхность, а с

помощью поверхностей различной формы и расположения можно ограни-

чить объем, построив, таким образом, тело. Геометрические точки – объекты

с нулевой массой и нулевым размером, поэтому отличить одну точку от дру-

гой можно по их различному положению в пространстве. Если располагать

точки по определенному закону, то можно построить объект, отображаю-

щий собой выбранную закономерность его построения.

В рассматриваемом примере числа X и Y «живут» парами. Поэтому

появляется идея – использовать эти пары чисел как расстояния для построе-

ния точки. Тогда, договорившись, откуда и как отмеривать эти расстояния,

построим множество точек, каждая из которых является образом пары чисел

– получится линия, наглядно отображающая ту самую зависимость, которая

связывает между собой Х и Y. Такова технология построения, например,

графиков функций.

Наиболее привычная ее реализация известна со школьной скамьи.

Через выбранное начало отсчета проводятся на плоскости две прямые, пер-

пендикулярные друг другу, указывающие направления, в которых нужно

отмеривать расстояния Х и Y (рис. 2.6). Получается прямоугольная коорди-

натная сетка – система координат имени Рене Декарта (1637). Каждая верти-

кальная линия в ней – это линия определенного и постоянного значения ве-

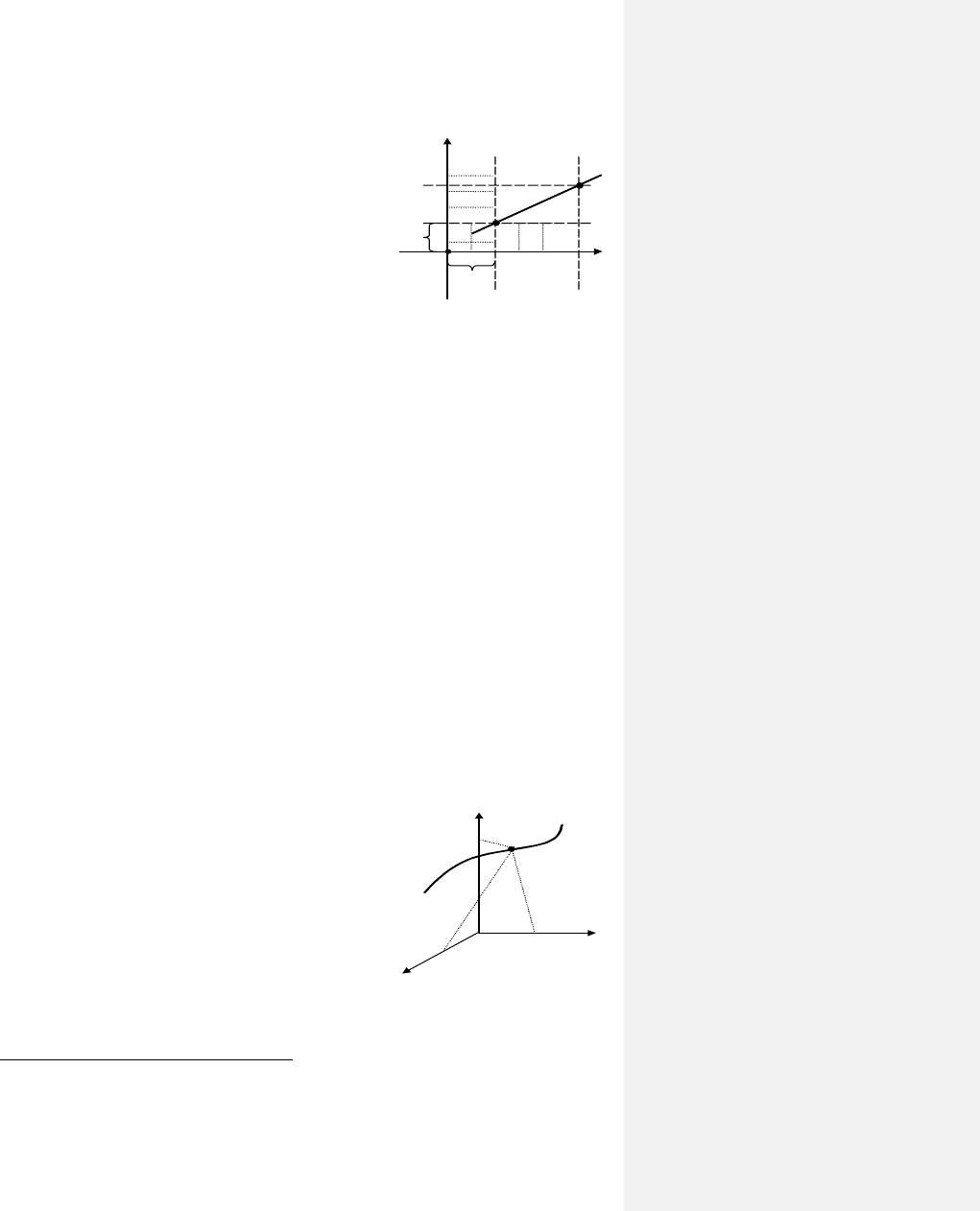
§ 11. Работа

личины Х, а горизонтальная, соответственно, Y.

Кстати говоря, нигде не написано, что коорди-

натные линии должны быть обязательно пря-

мыми и перпендикулярными друг другу. Это

стало привычным, видимо, потому, что повсе-

дневная наша жизнь проходит в пространстве,

ограниченном вертикальными стенами и гори-

зонтальными перекрытиями. Во многих отно-

шениях это удобно и технологично.

Но во многих ситуациях это и неудобно,

и невозможно. Взять, к примеру, глобус: коор-

динатные линии на нем не прямые, а окружности, и пересекаются они в ос-

новном не под прямыми углами. Но вернемся к диаграммам.

Для отображения связи между двумя величинами, как мы

видим, естественным путем появляется двумерная система коор-

динат. А уравнение состояния имени Клапейрона – Менделеева

связывает между собой три переменные величины. Отсюда дей-

ствительно следует возможность взять трехмерную систему ко-

ординат, откладывать по осям р, V, T и ввести, таким образом, в

оборот термодинамические диаграммы состояний (рис. 2.7).

Точка в такой диаграмме, имея координаты р, V и T, будет

отображать состояние системы, а последовательность точек-

состояний, линия — процесс. Правда, надо сразу оговорить, что

изображаемые и состояние, и процесс – равновесные (см. §7).

Диаграммы стали очень удобным, благодаря наглядности,

способом анализа термодинамических процессов

∗)

. Единствен-

ное, пожалуй, неудобство, с язанное с диаграммами – это по-

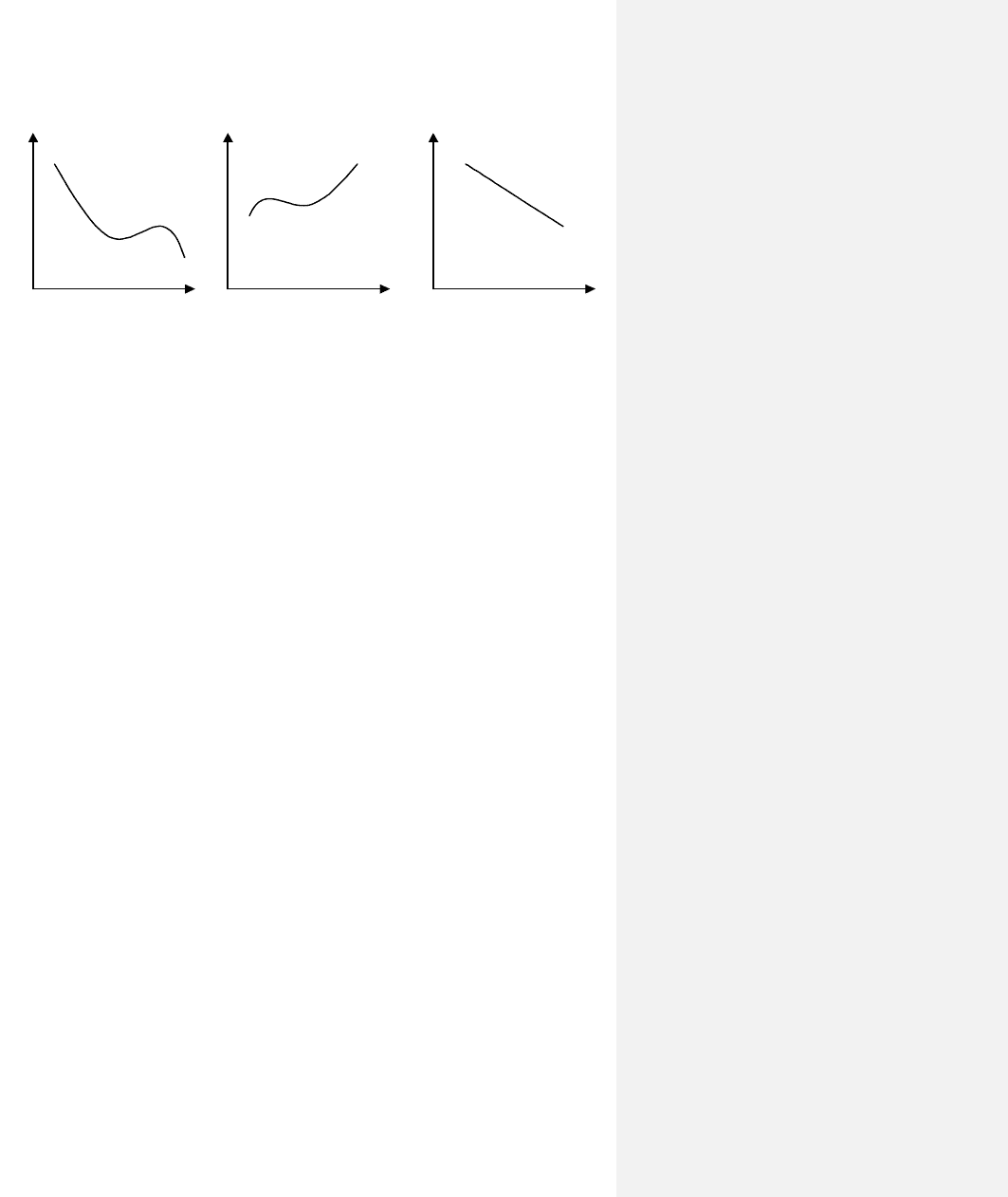
строение трехмерного изображения на

плоскости. Поэтому обычно вместо од-

ной трехмерной диаграммы используют

три двумерных — развертку. В каждой

из них линия, изображающая процесс,

является проекцией трехмерной кривой,

поэтому, как правило, один и тот же

процесс в разных диаграммах выглядит

по-разному (рис. 2.8).

∗)

Второй способ, абсолютно ненаглядный — математический. Оба

способа прекрасно дополняют друг друга.

Рис. 2.7. Термодинамиче-

ская диаграмма

Рис. 2.6. К построению

графиков функций

§ 11

. Работа

9.3. Модель строения вещества

Теперь осталось выяснить смысл понятия «идеальный

газ». Объекты, в названии которых есть слово «идеальный»,

существуют только в нашем сознании — это модели реаль-

ных. Про модели в начале главы говорилось, что это конст-

рукции, в том числе мысленные, в которых оставлены только

главные черты, качества, свойства моделируемого объекта, а

второстепенные отброшены. Идеальный газ — не исключение.

Идеальный газ — это модель строения вещества. Она

отражает наши представления о том, как вещество, наверное,

устроено внутри. Можно ответить иначе: это любое вещество

в газообразном состоянии, строго подчиняющееся уравнению

Клапейрона – Менделеева. Выясним, во-первых, какие же

свойства, качества вещества оставлены как главные, а какие

отброшены как второстепенные. Во-вторых, надо установить

область применимости модели, ведь будучи упрощенной кон-

струкцией, она не может работать всегда.

Модель по имени идеальный газ и смысл ее свойств ста-

ли понятны гораздо позже, чем появилось уравнение (2.2) –

лишь после утверждения молекулярно-кинетических пред-

ставлений о строении вещества. Свойства модели таковы.

1. Считается, что молекулы газа – материальные точки.

Это объекты нулевого размера, но при этом конечной, ненуле-

вой массы: d = 0, m ≠ 0. В природе нет таких объектов. Харак-

терный размер молекул ≈ 10

–10

м, конечно, мал, но это все же

не ноль. Тем не менее размером пренебрегают. При этом масса

≈ 10

-25

кг тоже весьма мала, а ею не пренебрегают. Почему?

Пренебрегать всегда естественно мелочью по сравнению

с чем-то крупным, но по смыслу родственным. В данном слу-

P P

V T

Рис. 2.8. Термодинамические диаграммы

§ 11. Работа

чае размер молекул естественно сравнивать со средним рас-

стоянием между ними

∗)

. Если оно велико (на порядок и более

превышает), то размерами молекул можно пренебречь. Опери-

руя не размерами, а объемами, можно сказать об этой ситуа-

ции так: если суммарный объем молекул мал по сравнению с

объемом, занятым газом, то им можно и пренебречь. Вывод:

газ должен быть достаточно разреженным.

Теперь о массе. Масса одной молекулы, конечно, мала

по сравнению со сколько-нибудь ощутимым количеством ве-

щества. Но если вещество состоит из молекул, то масса веще-

ства складывается из их масс. Если пренебречь массой моле-

кул, то любое количество вещества будет иметь нулевую мас-

су, не будет участвовать в гравитационном взаимодействии и

не будет сопротивляться изменению характеристик своего

движения. Это противоречит наблюдениям.

Кроме того, как упоминалось в гл. 1 при обсуждении

давления, благодаря тому, что молекулы газа взаимодейству-

ют со стенками сосуда в соответствии с законом сохранения

импульса, газ оказывает давление, которое может быть изме-

рено. Поэтому, лишая молекулы массы, мы лишаем их им-

пульса, а заодно и газ давления, что противоречит опыту. Зна-

чит, массой молекулы пренебречь нельзя.

2. Считается, что молекулы газа взаимодействуют

только при столкновениях – на расстояниях, равных нулю, а

на любых, бóльших нуля, никак не чувствуют друг друга.

Прямых очевидных возражений против этого нет, если

мы представляем молекулы в виде маленьких шариков. Но мо-

лекулы не шарики. И дело здесь, конечно, не в размерах. Про

шарик можно сказать, что это тело, обладающее замкнутой по-

верхностью, внутри которой сосредоточена вся его масса. Про

столкновение шариков можно сказать, что это ситуация, когда

их поверхности имеют хотя бы одну общую точку или когда

расстояние между двумя точками поверхностей равно нулю.

Про молекулы, даже простейшие одноатомные, такого

сказать нельзя. Практически вся масса атома сосредоточена в

∗)

Точнее – с длиной свободного пробега. Это среднее расстояние

между двумя последовательными столкновениями.

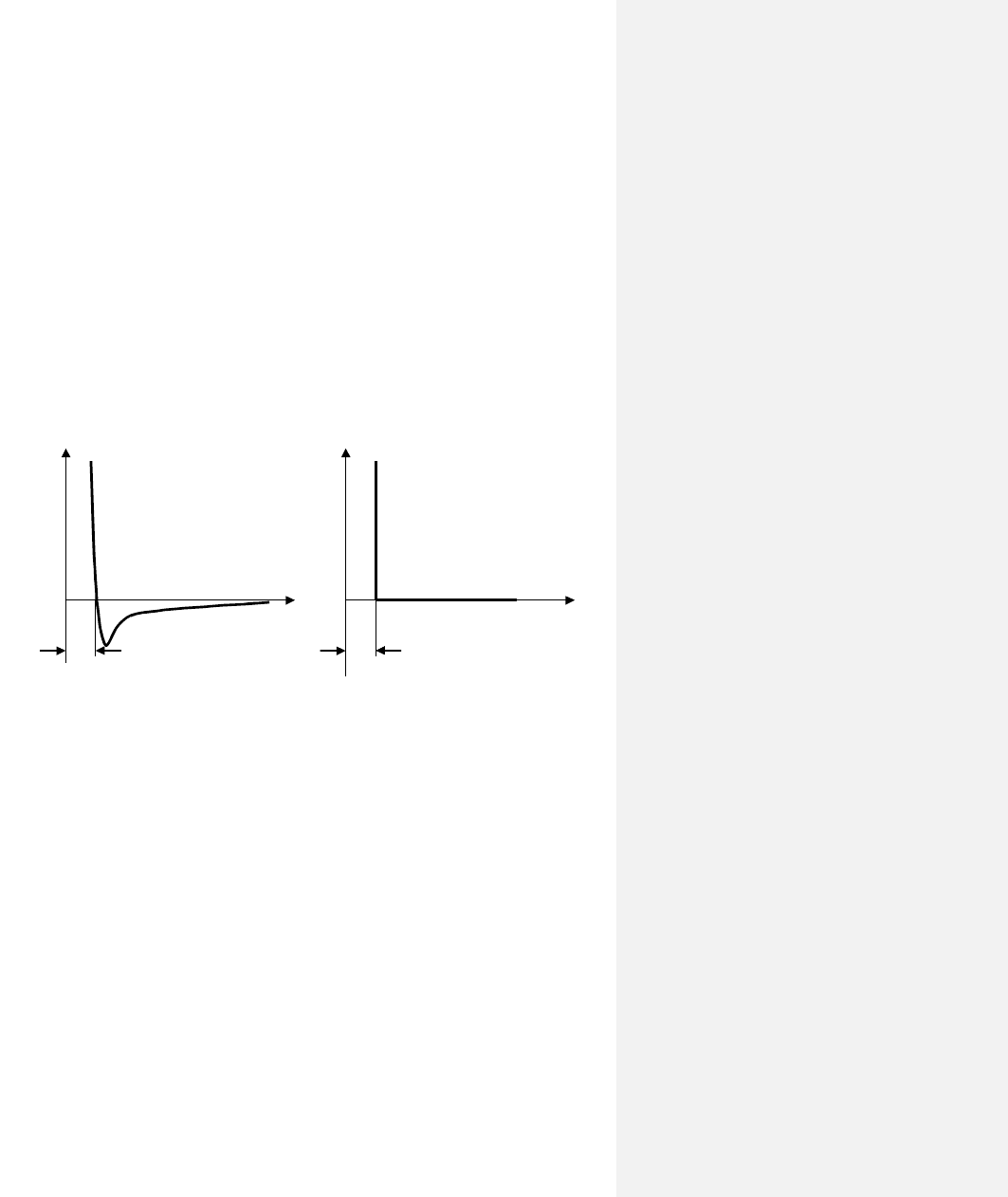
§ 11. Работа

его ядре, размер которого в сотни тысяч раз меньше размера

атома. Вокруг ядра стремительно движутся электроны, созда-

вая некое облако вероятностного присутствия. То есть нет от-

четливой замкнутой поверхности, внутри которой была бы со-

средоточена вся масса атома (молекулы). Поэтому говорить о

столкновении в обычном понимании не приходится. К тому

же, как показывает анализ многочисленных экспериментов,

взаимодействие молекул носит непрерывный, но неоднознач-

ный характер. Сближение на малых расстояниях (порядка

размера молекулы) приводит к резкому возрастанию сил от-

талкивания, а удаление на большие расстояния сопровождает-

ся убыванием до нуля сил притяжения (рис. 2.9).

Тем не менее, сопоставляя характер взаимодействия мо-

лекул и шариков, можно увидеть общее. Действительно, ого-

воренное отличие существенно лишь на малых расстояниях,

на которые в разреженном газе молекулы сближаются редко и

ненадолго. А значит, вклад такого отличия в общее поведение

газа в целом может оказаться незначительным.

Общий вывод из обоих свойств: любой газ можно считать

идеальным в разреженном состоянии. Но такой теоретический

вывод нельзя считать удовлетворительным с точки зрения ин-

женера. Непроизвольно разреженное состояние, т. е. состояние

с малой плотностью, ассоциируется с малыми давлениями и,

может быть, с вселенским холодом. В технике же очень часто

∼

мол

Е Е

шар

а б

Рис. 2.9. Зависимость энергии взаимодействия

при «столкновении» молекул (а) и шаров (б)

§ 11. Работа

приходится иметь дело с большими давлениями и высокими

температурами. Не призрачно ли тогда практическое значение

уравнения (2.6)?

Забегая немного вперед, можно пока ответить так. Лю-

бое вещество в газообразном состоянии можно считать иде-

альным газом вдали от состояний насыщения — тех, в кото-

рых газ готов сконденсироваться в жидкость. Для каждого ве-

щества это специфическая область состояний, но в целом она

характеризуется относительно низкими температурами. На-

пример, воздух — едва ли не самое распространенное рабочее

тело в технической термодинамике — может сконденсиро-

ваться в жидкость только при температурах, меньших –140 °С.

Поэтому при тех условиях, которые имеют место в тепловых

двигателях, топках котлоагрегатов и пр., воздух, конечно,

можно с достаточной точностью считать идеальным газом.

Вопросы для самопроверки

1. Что такое стационарное состояние?

2. Что такое стационарный процесс?

3. Как понимается состояние равновесия?

4. Что такое термодинамический процесс?

5. Что такое равновесный процесс? Каковы условия его реа-

лизации?

6. Что выражает уравнение состояния вещества?

7. Приведите общий вид уравнения Клапейрона – Менделеева.

8. Приведите частные случаи уравнения состояния идеально-

го газа.

9. Как определяется количество газа?

10. Что такое объемный расход, массовый расход?

11. Приведите уравнение состояния для потока газа.

12. Что такое термодинамическая диаграмма?

13. Что изображается в термодинамических диаграммах?

14. Каковы свойства идеального газа?

15. Каковы условия применимости модели идеального газа?

§ 11. Работа

т:

ГЛАВА 3

ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ

§ 10. Уравнение первого начала термодинамики

Первое начало, или первый закон, термодинамики —

это не что иное, как частный случай общего закона сохране-

ния энергии. Частный случай связан с теми процессами, ко-

торыми занимается термодинамика. Изначально речь шла о

процессах взаимного превращения тепла и механической ра-

боты, а впоследствии, как уже упоминалось, «кругозор» был

существенно расширен.

Часто фундаментальные мысли, которые становятся за-

конами, приходят практически одновременно многим, и фор-

мулировок законов бывает несколько

∗)

. Одна из них для перво-

го начала термодинамики гласи

тепло, подведенное к системе, расходуется на изме-

нение внутренней энергии вещества и на работу процесса, в

ней происходящего.

В виде уравнения эта фраза выглядит так:

Q = ΔU + L, (3.1)

где Q – тепло процесса;

ΔU – изменение внутренней энергии системы;

L – работа.

Таким образом, первое начало устанавливает количест-

венное соотношение между тремя энергетическими величина-

ми, поэтому обсудим каждую из них.

∗)

В связи с первым началом термодинамики необходимо упомянуть имена

авторов: Майер (1842), Джоуль (1843 – 1847), Гельмгольц (1847). Уравнение

в виде (3.1) записано Клаузиусом в работе, посвященной второму началу

термодинамики (1864).

§ 11. Работа

Во введении говорилось о том, что понятие работы, появ-

ляющееся в механике, в первозданном виде относится к про-

цессам, связанным с движением тел как целых объектов. Тех-

ническая термодинамика занимается процессами, происходя-

щими в веществе, в телах независимо от их движения или по-

коя. Понятие работы, особенно когда речь идет о тепловом

двигателе, весьма привлекательно, но прежде чем его исполь-

зовать для характеристики термодинамических процессов,

нужно найти для этого основания.

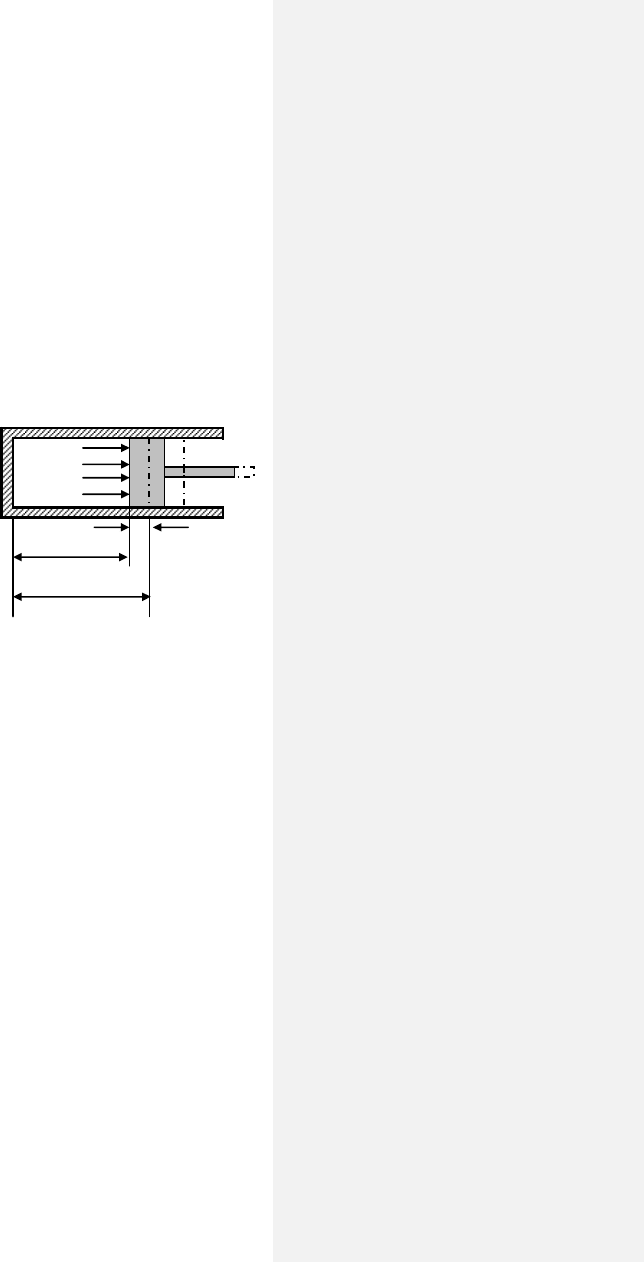
Используем традиционную

систему цилиндр – поршень с газом

(рис. 3.1). Дадим газу возможность

немного расшириться, подвинуть

поршень на малое расстояние ΔХ.

В такой ситуации можно найти

основания для применения понятия

работы. В самом деле, есть тело —

поршень, которое совершило

перемещение. К поршню приложена сила – сила давления со

стороны газа (рис. В.2.). Поэтому можем применить выраже-

ние (В.1) к рассматриваемой ситуации на полном основании,

учтя, что направления действия сил и перемещения совпадают

(cos α = 1):

Рис. 3.1. О работе газа

L = F

cos α = p

Х·1. (3.1)

Здесь S – площадь поршня. Произведение pS дает со-

ставляющую сил давления, которая совершает работу — из

всех поверхностей, ограничивающих объем газа, перемещает-

ся только поверхность поршня.

Если теперь обратить внимание на произведение S

Х, то

это будет объем, заключенный между начальным и конечным

положениями поршня — приращение объема газа

V = V

– V

Тогда

L = p ·

V. (3.2)

Этот результат замечателен тем, что, во-первых, процес-

су, произошедшему в газе, удалось сопоставить механическую

§ 11. Работа

характеристику — работу; во-вторых, величина работы в газо-

вом процессе выражена только через параметры состояния газа.

Проверим размерность:

[L] = [p] · [V] = Па · м

= (н/м

) · м

= н · м = Дж, как и

должно быть в системе СИ.

Теперь займемся следствиями, вытекающими из полу-

ченного результата.

1. Давление в (3.2) – абсолютное. Именно оно является

термодинамическим параметром состояния (см. § 6) и при

этом всегда положительно. Изменение объема же может

иметь разный знак в зависимости от того, что происходит с

газом, а именно:

а) расширение — увеличение объема: ΔV > 0. Значит,

работа – число положительное, L > 0. В этом случае принято

считать, что газ совершил работу над внешними силами;

б) сжатие: ΔV < 0, L < 0. Внешние силы совершают

работу над газом;

в) процесс происходит при неизменном объеме газа:

V = consT, ΔV = 0, L = 0. Работа не совершается.

Эти три пункта представляют собой «внутритермодина-

мическое» правило знаков для работы.

2. Выражение (3.2) и правило знаков позволяют сфор-

мулировать термодинамическое определение работы.

Работа – это величина, характеризующая способ обме-

на энергией, однозначно связанный с изменением объема.

В этом определении слово «величина» в очередной раз

напоминает о том, что работа в термодинамике – численная,

энергетическая характеристика процесса, а не сам процесс.

3. При получении выражения (3.2) сделана оговорка

о том, что процесс – маленький. Это значит, что изменением

давления по сравнению с величиной давления можно пре-

небречь, считая его постоянным. Выражение (3.2) относится

к одному частному случаю и требует обобщения на любой

процесс. Для этого в качестве инструмента анализа использу-

ем диаграмму p-V, поскольку в выражении (3.2) фигурируют

именно эти параметры.

На рис. 3.2 изображен процесс, в котором газ изрядно

расширился от объема V

до объема V

. При этом его давление