Панов В.К. Физические основы теплотехники. Ч. I: Термодинамика

Подождите немного. Документ загружается.

§ 44. Испарение и кипение 187

е а точка попадает на

интервал значений

жно разделить про-

, на которые точка

к расстояние между

обавить к меньшему

т интерполяцией.

бнее пользоваться для расчетов в тех

риваемый процесс не ограничивается

от о

ку с и-

–5

значащ

пию и энтропию. Чтобы определить р,

v, Т или х, нужно уви-

деть, какая изобара, изохора, изотерма или линия постоянной

сухости проходит через точку и взять соответствующее ей

значение. И это все с одной диаграммы!

Конечно, н всегд

линию. В этом случае

на соседних линиях ну

порционально отрезкам

делит геометричес ое

линиями (рис. 8.15), и д

значению. Это называю

Диаграммами удо

случаях, когда рассмат

областью только ВП. Х

менее точный, посколь

чину в лучшем случае с тремя знаками, а таблицы дают 4

bbbb

121

)( −+=

я при этом расчет будет нескольк

диаграммы можно получить вел

их цифры.

Еще одно удобство диаграмм состоит в том, что любая

изображенная в ней линия соответствует какому-либо изопро-

цессу. Например, в i-s диаграмме вертикальные линии изо-

бражают адиабатный процесс (s = const, см. § 27, свойство 3),

горизонтальные – процесс дросселирования, о котором пойдет

речь в следующем параграфе, и так далее. Это очень помогает

при решении задач и анализе процессов.

§ 44. Испарение и кипение

Процессы испарения и кипения с позиций термодинами-

ки — это один процесс: фазовый переход жидкость – газ, па-

рообразование. Оба они могут протекать равновесно только

при достижении системой состояния насыщения – при темпе-

ратурах ниже Т

кр

. И в том и в другом случае необходимо подво-

дить к жидкости теплоту парообразования. В обоих случаях сте-

пень сухости в закрытой системе изменяется от 0 до 1, а удель-

ный объем – от

v' до v''. Но практическое осуществление про-

цессов обнаруживает существенное различие в условиях и ха-

рактере их протекания (что вполне отчетливо видно глазом).

Рис. 8.15. Об интер-

поляции

§ 44 ение . Испарение и кип18

ра у них оди-

(8.1а, 8.1б). Если над поверхностью

находится смесь ее пара с другим

например, воздухом), то, по закону

на, к жидкости будет приложено их

рное давление (рис. 8.16). В этом слу-

ловие равновесия (8.1а) изменится:

= р

пар

+ р

газ

Присутствие постороннего газа влияет на интенсивность

испарения. Поэтому, в частности, снижение давления воздуха

ускоряет процесс при вакуумной сушке.

Кипение – это парообразование в объеме перегретой

жидкости. В пояснении здесь нуждаются слова «в объеме»

и «перегретой».

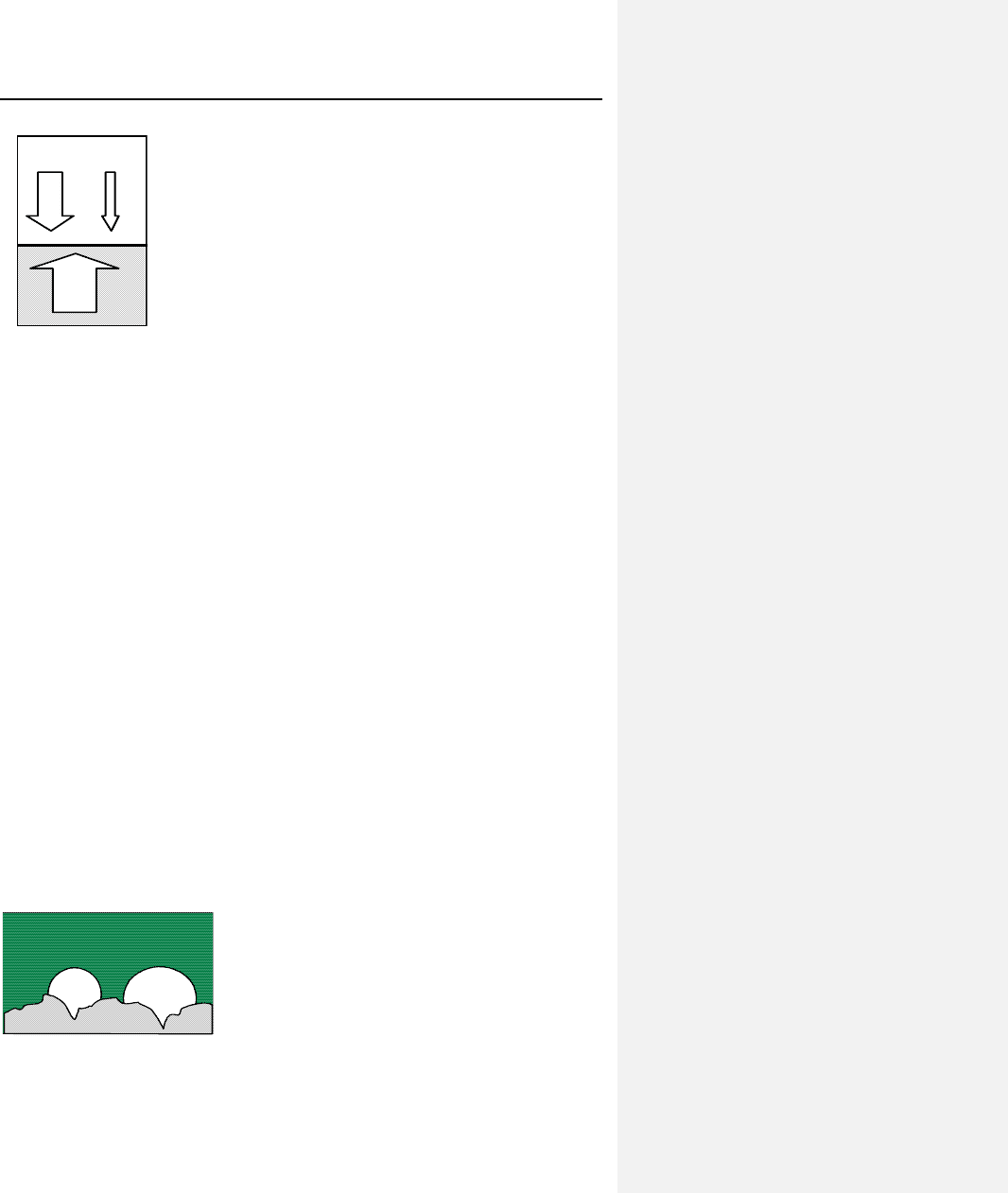
При кипении пар образуется в виде пузырей, которые

возникают на греющей поверхности, расположенной внутри

жидкости (рис. 8.17). Пузырь растет, окруженный жидко-

стью, в ее объеме.

Для перехода вещества из окружающей жидкости в па-

ровой пузырек жидкость должна иметь темп -

ния при давлении СНП в пузыре:

Дж/м

;

R – радиус пузыря.

Большему давлению соответст-

вует и бóльшая темпе

щения. Значит, в тонк

зи греющей поверхности, где появ-

ляются и растут пузыри, жидкость

должна иметь более высокую тем-

пературу, чем в остальном объеме.

Испарение – это парообразование со

свободной поверхности жидкости.

Если жидкость по свободной поверх-

ности контактирует только со своим же па-

ром, то давление и температу

наковы

жидкости

газом (

Дальто

сумма

чае ус

ературу насыще

жидк

= Т

(р

пар

Давление пара в пузыре больше, чем в окружающей его

жидкости, на величину, добавляемую поверхностным натяже-

нием. Поэтому условие (8.1а) принимает вид

пар

= р

жидк

+ 2σ/R, (8.20)

где σ – коэффициент поверхностного натяжения, н/м =

ратура насы-

ом слое вбли-

Рис. 8.16. Равнове-

сие жидкости и

парогазовой смеси

Рис. 8.17. Образование

ост па

овых п

зы

ей

§ 45. Процесс дросселирования 189

В этом смысле жидкость и должна быть перегретой.

Величина перегрева зависит от множества причин. Все они

связаны с механизмом образования пузырей, а его рассмот-

рение выходит за рамки нашего курса. Но все же главные

причины назовем.

Пузыри образуются на неоднородностях, которыми мо-

гут быть: неровности (шероховатость) греющей поверхности,

твердые частицы взвеси, пузырьки растворенного газа и т. д.

Если жидкость очень чистая, греющая поверхность очень

гладкая, внешние воздействия сведены к минимуму, то пе-

регрев может быть весьма значительным. В таких условиях

вода, например, при атмосферном давлении вместо положен-

ных 100

°С может оставаться некипящей вплоть до 140–150 °С.

Это состояние неустойчивого равновесия. Но стоит только

внести малейшее возмущение – скажем, слегка щелкнуть по

сосуду, – как кипение практически мгновенно охватывает весь

объем (пузыри будут образовываться не только на греющей

поверхности) и температура приходит «в норму».

В «нестерильных» технических условиях центрами па-

рообразования в основном являются элементы шероховатости

греющей поверхности, средний размер которых определяет

размер устойчивых пузырей (R в формуле (8.20)) и, таким обра-

зом, перегрев, необходимый для начала устойчивого кипения.

§ 45. Процесс дросселирования

Изопроцессы, подробно рассмотренные для идеального

газа, протекают и с участием ВП, и с жидкостью. Правда, они

описываются уже другими уравнениями и изображаются по-

рой другими линиями в диаграммах. Но есть еще процесс,

представляющий интерес именно с реальным веществом —

это дросселирование.

Дросселирование

∗)

— это процесс понижения давле-

ния при прохождении потоком вещества концентрирован-

ного гидравлического сопротивления. Дросселем может быть

шайба, вентиль, пористая, но проницаемая пробка — любое

∗)

От немецкого слова, означающего «душить».

§ 45 ия . Процесс дросселирован19

устройство со значительно меньшим

проходным сечением, чем до и по-

сле него.

Пояснение придется начать

с упоминания о гидромеханике.

Движению жидкости или газа по

трубе всегда мешает сопротивление

со стороны трубы, связанное с вязко-

стью вещества. Для его преодоления

необходим перепад давления. Труба

для потока – непрерывное (протя-

женное) гидравлическое сопротив-

ление. Кроме этого, на пути пото-

ка встречаются повороты, изменения проходного сечения в

различных устройствах. Эти неоднородности меняют струк-

туру потока и поэтому являются дополнительными местными

гидравлическими сопротивлениями. Часто величина их намного

превосходит сопротивление многих метров прямой трубы до и

после неоднородно ое гидравличе-

ское сопротивление» подразумевают, что сопротивлением тру-

бы до и после дросселя (перепа

пренебречь по сравнению с д

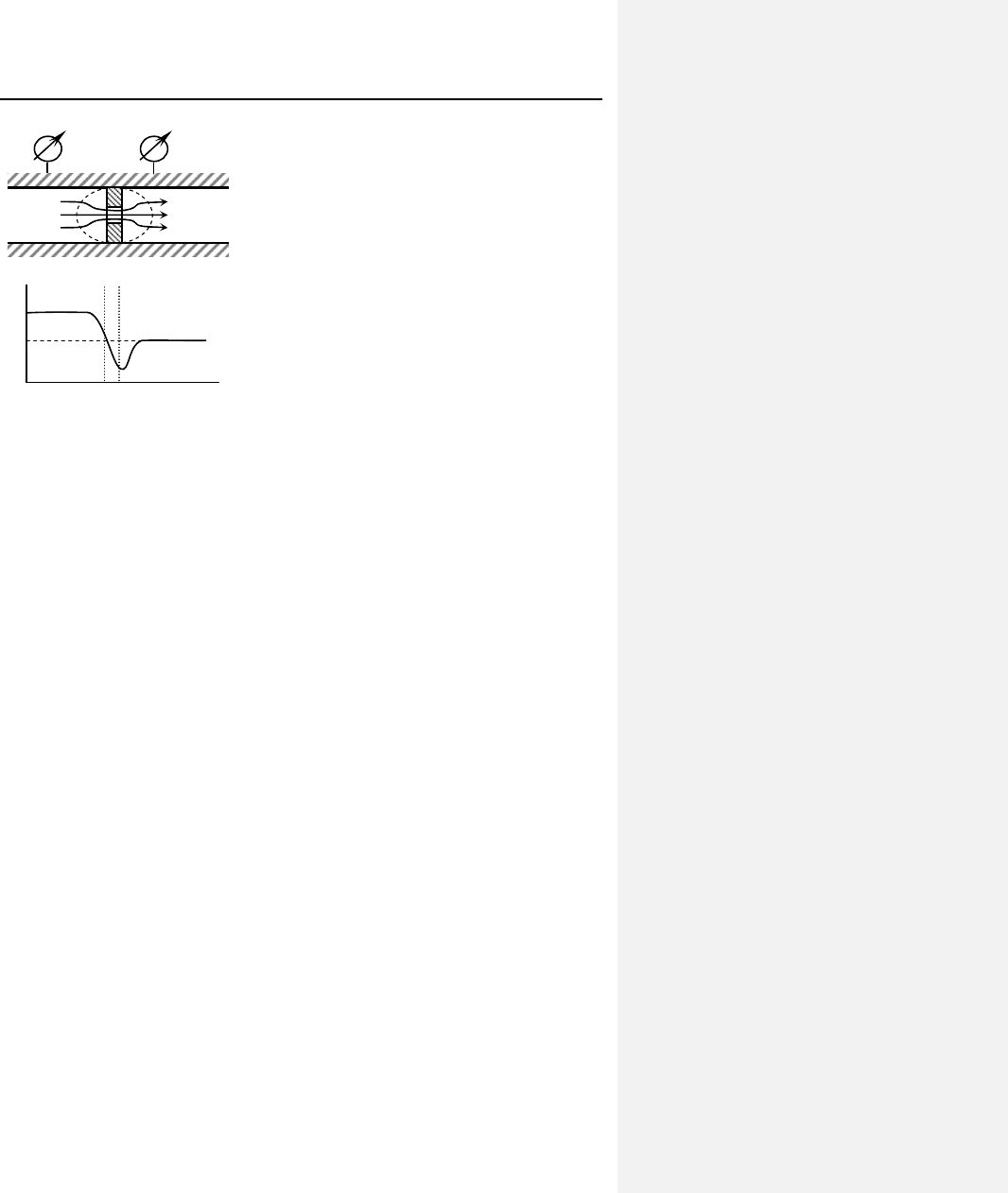
На рис. 8.18 схемат

процесса дросселирования

Первое, на что над

дросселем (по ходу пото

Согласно закону Бернулл

(в дросселе) поток ускор

Пройдя дроссель, поток р

в нем подрастает, но не до

< р

сти. Слова «концентрированн

дом давления на ней) можно

сопротивлением самого росселя.

ично изображены основные черты

о обратить внимание: давление за

ка) всегда меньше, чем перед ним.

и при прохождении узкого сечения

яется, а давление в нем снижается.

асширяется, тормозится и давление

прежней величины р

, а до меньшей

(рис. 8.18). Это происходит из-за действия сил вязкости, на

работу против которых поток тратит часть своей энергии.

Поток никогда не идет из области с меньшим давлени-

ем в область с бóльшим. Поэтому процесс дросселирования

принципиально необратим.

Второе: изменение параметров состояния, связанное с

дросселированием, происходит в непосредственной близости

от дросселя (пунктирная область на рис. 8.18). Это область

Рис. 8.18. Схема процесса

дросселирования

Др

§ 45. Процесс дросселирования 191

еняется скорость

. Но кинетиче-

дросселирова-

малы по сравне-

ещества. Сделаем

ре Т = 300 К для

потока

место, равное удельному

, с

малых размеров, и вещество проскакивает ее быстро — на-

столько, что теплообменом потока с самим дросселем можно

пренебречь. Поэтому практически всегда рассматривают

адиабатное дросселирование.

Третье: при прохождении дросселя изм

потока – изменяется его кинетическая энергия

ской энергией и тем более ее изменением при

ния пренебрегают, поскольку эти величины

нию с внутренней энергией и энтальпией в

оценки на примере идеального газа.

Для 1 кг газа i = c

Т. При температу

возду

ха i = 10 ·300 = 300 кДж/кг. Кинетическая энергия ки-

лограмма газа при скорости, например, 10 м/с составит: Е =

= mw

/2 = 1·10

/2 = 50 Дж/кг. Даже при скорости 100 м/с (что

очень много для технологических процессов) Е = 5 кДж/кг.

Это всего 1,7 % энтальпии.

Итак, необратимый процесс адиабатного дросселирова-

ния при неизменной, малой кинетической энергии об-

ладает следующими особенностями.

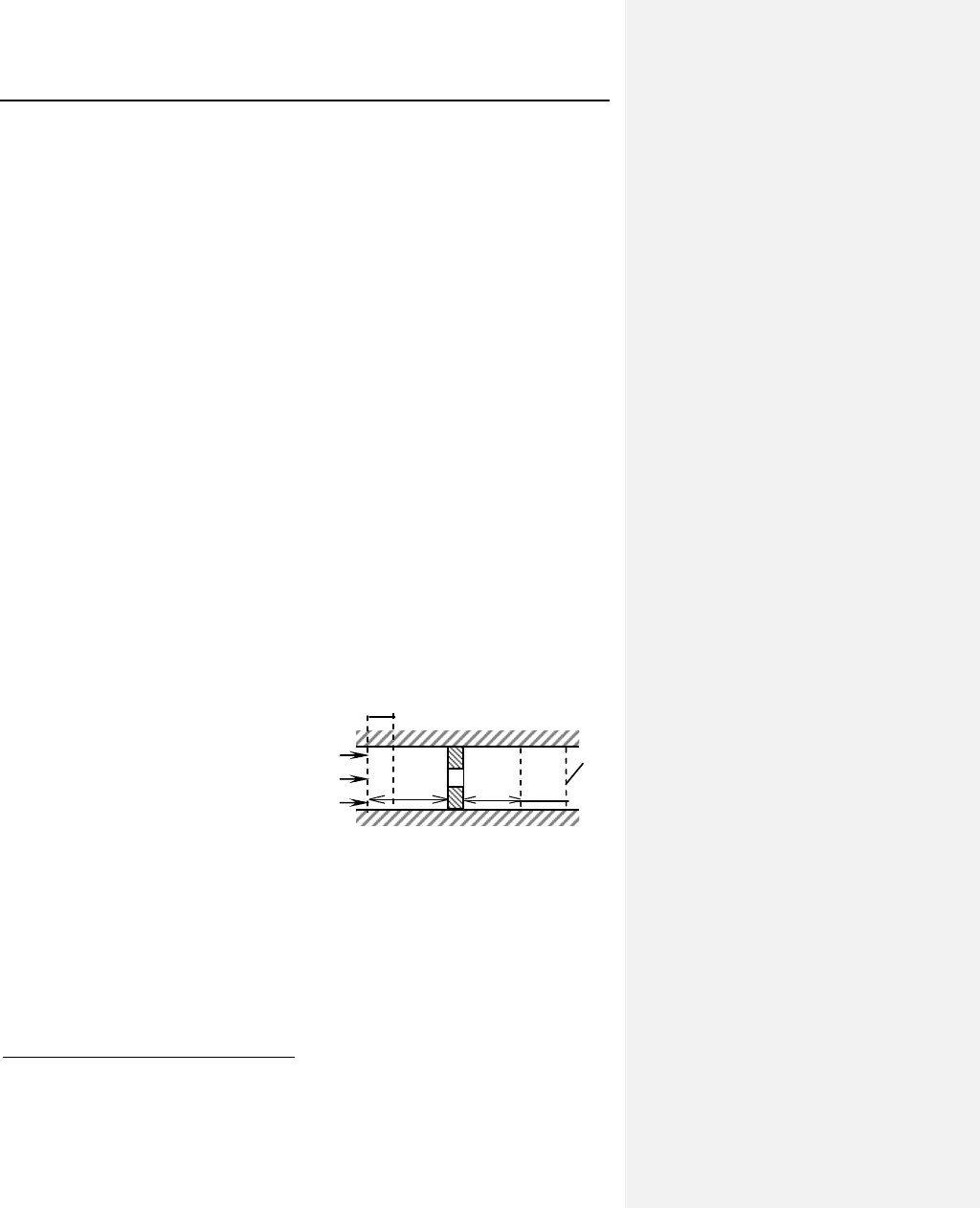
Изоэнтальпийность. Пусть через сечение I прошел 1 кг

газа (см. рис. 8.19). Одновременно такое же количество газа

пройдет через сечение II, только оно будет при меньшем дав-

лении занимать другой объем.

Чтобы ввести в трубу 1 кг

газа, ему нужно освободить там

объему

∗)

. Для этого придется

подвинуть газ массой m = m +

осредоточенный между

сечениями I и II, а это значит

затратить работу. Давление

вдоль по потоку, как уже отмечено выше, практически не ме-

няется вплоть до дросселя и затем после него. Работа сил дав-

ления по перемещению газа от сечения I до сечения I' соста-

вит:

I–I'

= р

I–I'

= (объем между сечениями I и I′ равен

∗)

Напомню, что по определению удельный объем — это объем 1 кг

вещества.

Рис. 8.19. Об изоэнтальпий-

ности дросселирования

Др

I I

′

II II

′

§ 45. Процесс дросселирования 192

удельному — ввели 1 кг газа

Эта работа с L

I–I'

< 0.

Килограмм газа, п

совершает работу,

Примéним п

изошедшему с вещ

т о

б ва

1 1 2 2

v – р v ⇒ u + р v = u + р v ⇒

нии н меняется. Отсюда ние процесса – изоэн-

тальп

овными. Название по-

тому, что одинаковы тольк

Дросселирование –

в потоке. Изменение про

вентиля, задвижки и т. д.

ние за дросселем, а заодн

широко применяется в Н

из и р

р ст а

) = р

. (а)

овершается над веществом потока —

роходящий через сечение II, уже сам

освобождая себе место:

II–II'

= р

(> 0). (б)

ервое начало термодинамики к процессу, про-

еством, находящимся между сечениями I и II:

Q = ΔU + L.

надо понимать сумму работ (а) и (б) с уче-

ложных знаков. Эту величину называют ра-

ния.

Под L здесь

ом их противоп

отой проталки

Внутренняя энергия газа, находящегося между сечения-

ми I и II (начальная), складывается из составляющих ее частей:

= m

+ m

Внутренняя энергия того же газа, но между сечениями I'

и II' (конечная, после прохождения 1 кг газа) составит:

= (m – 1 кг)u + (m + 1 кг)u .

Тогда ее изменение в результате процесса

ΔU = m

– u

+ m

+ u

– m

= u

– u

Поскольку процесс адиабатный, то

0 = u

– u

+ р

2 2 1 1 2 2 2 1 1 1

⇒ i

= i

. (8.21)

Таким образом, энтальпия вещества при дросселирова-

е второе назва

ийный. В диаграмме i-s он изобразится отрезком горизон-

тальной прямой, в диаграмме р-i — вертикальным отрезком.

И название, и изображение следует считать усл

о начальное и конечное значения энтальпии, а в

течение процесса она изменяется. Изображение потому, что процесс необра-

тимый и неравновесный.

простой способ понижения давления

ходного сечения дросселя (с помощью

) позволяет легко регулировать давле-

о и расход потока. Благодаря этому он

различном оборудовании. апример,

асхода пара, подаваемого на турбину,

ь. Впрочем, это довольно очевидно н

менением давления

егулируется ее мощно

§ 45. Процесс дросселирования 193

приме

ничестве с Уильямом Томсоном (сэром

Кельв

−

приводит к тому, что за дросселем

При увеличении Т

эффект ослабе-

вает д

тет до макси-

мума

нижением температуры. Начальные состояния за ее пределами

ре обычного водопроводного крана. Неочевиден темпера-

турный эффект, связанный с дросселированием.

Изменение температуры. Такой эффект, связанный с

дросселированием, экспериментально исследован Джеймсом

Джоулем в сотруд

ином) в 1852 – 1854 гг. и с тех пор носит их имя.

Эффект Джоуля – Томсона состоит в том, что темпе-

ратура газа при дросселировании может изменяться. Обра-

щаю внимание на деликатность слов «может изменяться».

Помимо того, что это означает «может и не изменяться», из-

менение — это и понижение, и повышение. В тех условиях, в

которых экспериментировали Джоуль и Томсон, у всех

«нормальных» газов температура за дросселем была ниже,

чем перед ним. Исключением был водород, который демон-

стрировал повышение температуры.

Дальнейшие исследования показали, что знак и вели-

чина эффекта зависят:

−

от вещества (в одних и тех же условиях);

состояния перед дросселем (для выбранного вещества).

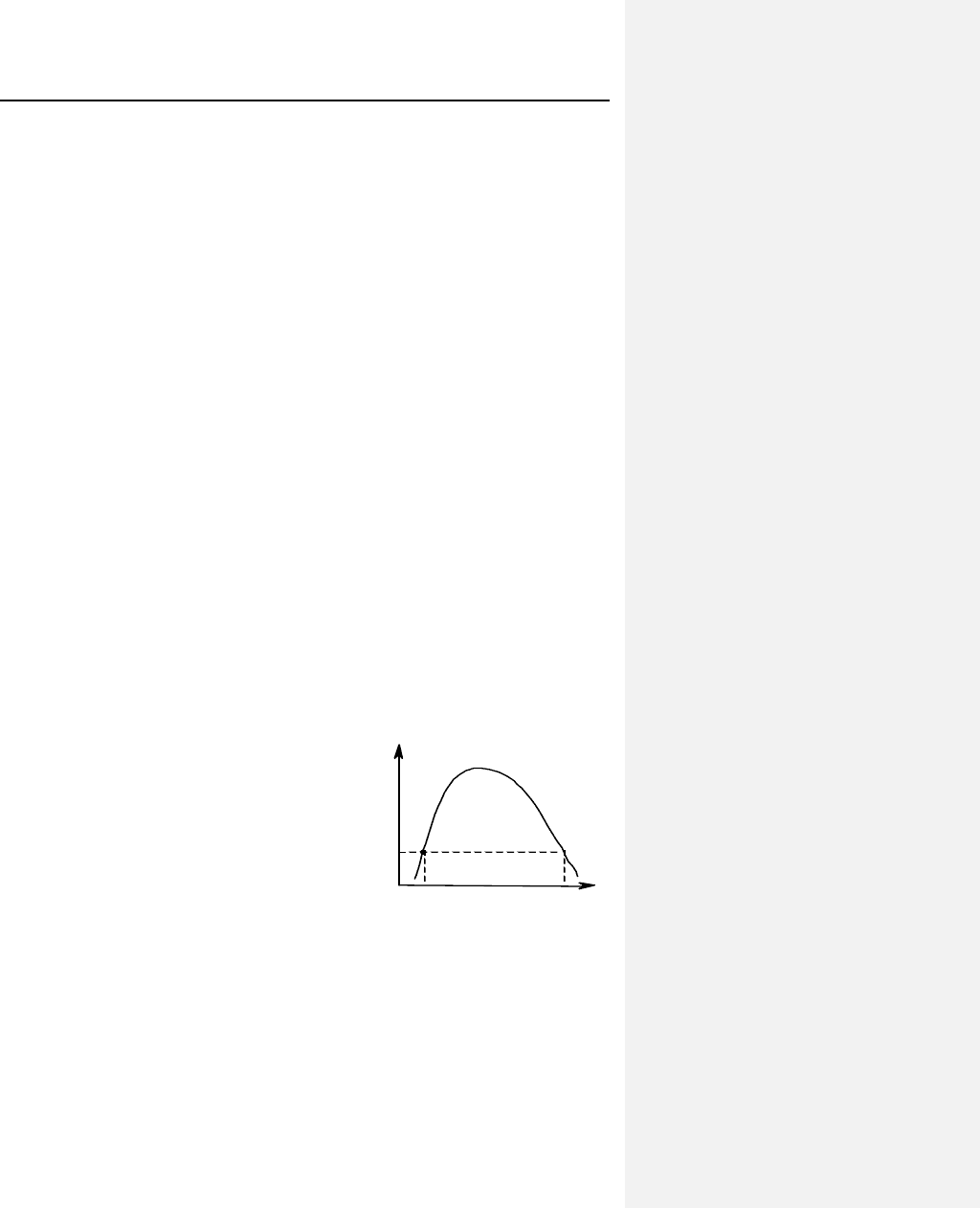
Для пояснения используем р-Т диаграмму, на которой

отмечаются только состояния перед дросселем с параметрами

и Т

(рис. 8.20). Если процесс начинать при одном и том же

давлении р

аб

, то при малых значениях Т

дросселировани

температура выше, чем перед ним.

о нуля при некотором значе-

нии Т

. Дальнейшее увеличение Т

приводит к обратному эффекту – за

дросселем температура меньше, чем

перед ним. Далее, вслед за Т

раз-

ность температур рас

и снова убывает до нуля при значении Т

. При переходе

через состояние б эффект снова меняет знак. Эксперименты,

проведенные при разных давлениях, оконтуривают область

состояний, дросселирование из которых сопровождается по-

Рис. 8.20. Кривая инверсии

> 0

< Т

аб

2 1

< 0

Т > Т

; Т

> Т

§ 45. Процесс дросселирования 194

привод к повыш ю те

Кривая инверсии —

дросселировании из которых т

Латинское слово «инверси з

когда что-то изменяется с

случае меняется ха

= Т

– Т

. Если

ратура при

высится.

Кривая инверсии дл

та кри

ся .

ссел

ят ени мпературы.

это область состояний (а и б), при

емпература не изменяется.

я» часто исполь уют в тех случаях,

точностью до наоборот. В данном

изменения температуры, т. е. знак

ое состояние попадает под кривую,

овании понизится, если за кривую –

я каждого вещества индивидуальна,

вая и линия насыщения. Определяет-

ь-эффекта судят по коэффициенту

адиабатного дросселирования

рактер

начальн

дросселир

ΔТ

темпе

по

к же как пограничная

она экспериментально

О величине дро

consti

≅

⎟

⎠

⎞

⎜

⎝

⎛

∂

ое дросселирование,

сне-

ния и

температуры – при дросселиро-

вании

, К/Па, (8.22)

который показывает, на сколько градусов изменяется темпера-

тура при изменении давления на единицу. За дросселем давле-

ние всегда меньше — Δр < 0, поэтому

> 0 – соответствует понижению температу-

ры, ΔТ < 0;

< 0 – соответствует ее повышению, ΔТ > 0; (8.23)

= 0 – изотермическ

ΔТ = 0.

Строгое равенство в выражении (8.22) относится к так

называемому дифференциальному дроссель-эффекту, т. е. когда

изменение давления бесконечно малó (практически это 1 бар).

Приближенное равенство в (8.22) соответствует интегрально-

му эффекту — при значительном изменении давления. Кривая

инверсии соответствует дифференциальному эффекту.

В интегральном эффекте не все так просто. Для поя

спользую кривую инверсии, построенную в Т-s диаграм-

ме (рис. 8.21). По-прежнему начальное состояние под кривой

приводит всегда к понижению

до любого более низкого давления (рис. 8.21, а). Если

же начальное состояние находится за кривой инверсии (рис.

8.21, б), то конечная температура будет больше начальной

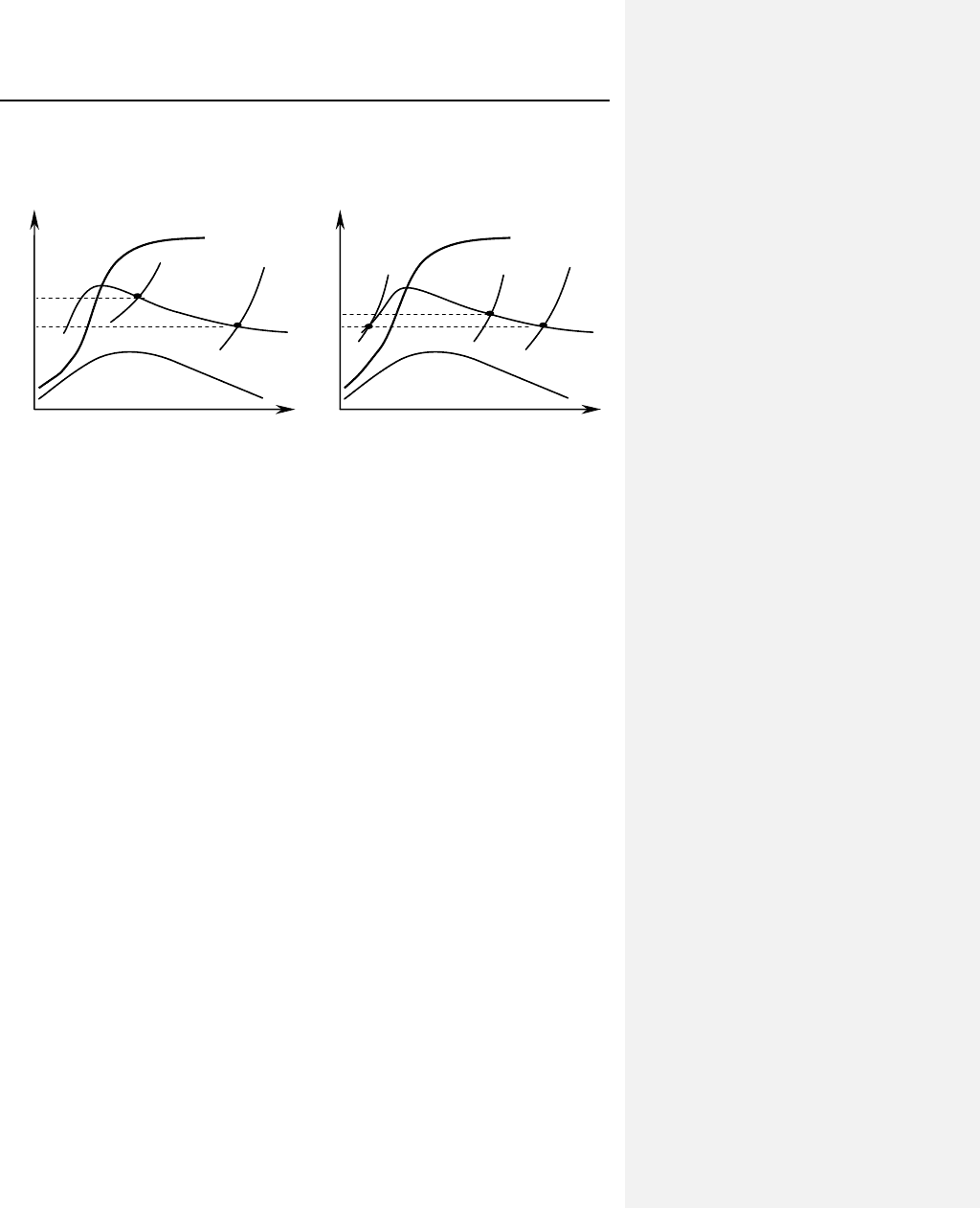
§ 45. Процесс дросселирования 195

а л

иви-

ры. Пр

отив них надо все-таки затратить ра-

я. Но работа, затраченная против сил

ь работа проталкивания), «возвра-

тепло выделяется во всем объеме по-

ижения температуры можно ожидать,

при отсутствии вязкости. Во всяком

ышения.

ину могут такие соображения. Из ра-

(= Q

трения

). (8.24)

изменении давления. В свою очередь, изменение удельного объема опреде-

ляется

вплоть до давления, соответствующего точке 2'. Для практи-

ческого определения ΔТ пользуются специально построенны-

ми диаграмм ми дроссе ь-эффекта для разных газов.

Неоднозначное поведение

тельно

температуры при дросселировании уд

и, надо признать, в рамках равновесной термодинамики ясного тол-

кования не находит.

В самом деле, вполне привычно, что газ, попадая из области высоко-

го давления в область более низкого, расширяется с понижением температу-

и отсутствии теплообмена это связано с расходованием внутренней

энергии на работу против внешних сил (§ 18). В данном случае нет внешних

по отношению к потоку сил — температура не должна измениться.

Правда, хоть и нет внешних сил, зато есть силы «внутреннего тре-

ния т», вызванные вязкос ью. Значит, пр

боту, и температура должна понизитьс

любого трения-сопротивления (это и ест

щается» полностью в виде тепла. Это

тока и усваивается им же. Значит, пон

но, быть может, в меньшей степени, чем

случае, вроде бы неоткуда ждать ее пов

В общих чертах прояснить карт

венства энтальпий (8.21) следует:

ΔU = –L

протал

Это значит, что тепло, полученное от трения, полностью возмещает

убыль внутренней энергии. У идеального газа она состоит только из кинети-

ческой энергии молекул и однозначно связана с температурой. Поэтому иде-

альный газ дросселируется изотермически.

Равенство (8.24) справедливо и для реального газа, но у него внут-

ренняя энергия кроме кинетической составляющей содержит еще и потен-

циальную. Она связана с удельным объемом (§ 12), который изменяется при

таким физическим свойством, как сжимаемость вещества. Значение

Кривая инверсии

const

ПК

Кривая инверсии

′

ПК

′

Рис. 8.21. Интегральный дроссель-эффект из начального состояния:

а – под кривой инверсии; б – за ее пределами

§ 45. Процесс дросселирования 196

же коэ

разных

потенц

ления рный эффект

дросс

погрешностью не более 1–2 %.

темпе о, менее термодина-

мичес

еля по

сравн андером (уст-

ройст боты) гораздо

больше , тру-

дозат позво-

ляющ ры,

не им

А см

очень

измен

ффициента сжимаемости у одного и того же вещества различается в

областях состояний.

Таким образом, изменение температуры определяется перераспреде-

лением джоулей между тремя величинами: кинетической энергией молекул,

иальной энергией молекул, работой проталкивания.

Для процессов, происходящих при сравнительно высоких

температурах (ориентировочно > 0 °С) и не очень больших дав-

х (ориентировочно < 100 бар), температу

елирования не имеет существенного значения. К тому же

он мал, поскольку в этой области технически важные газы ве-

дут себя как идеальные с

Весьма полезным эффект Джоуля – Томсона оказался

для холодильной и криогенной техники. Получение низкой

ратуры дросселированием, конечн

ки эффективно, чем путем обратимого адиабатного рас-

ширения. Но выгода от простоты конструкции дросс

ению с поршневой машиной или турбодет

вами для расширения с производством ра

. Кроме выигрыша в габаритах, металлоемкости

ый вентиль, ратах при изготовлении дроссельн

ий легко регулировать величину снижения температу

еет подвижных трущихся частей, которым нужна смазка.

азка в условиях низких температур — это проблема с

дорогостоящими решениями. Поэтому дроссельный

вентиль (по терминологии холодильщиков – ТРВ) — неотъем-

лемый элемент всех промышленных холодильных установок.

Свойство эффекта (особенно интегрального) коварн

ять знак, инверсию приходится учитывать в криогенной

технике (в области температур ниже –150 °С), при производ-

стве сжиженных газов, особенно водорода и гелия.

Вопросы для самопроверки

Как, по каким признакам отличают вещества друг от друга?

С чем связано различие в свойствах жидкости и газа одно-

го и того же вещества?

Что такое теплота парообразования?

На что расходуется теплота парообразования?

Что требуется для того, чтобы 1 кг жидкости превратился в

1 кг пара?