Основы математической логики и теории алгоритмов
Подождите немного. Документ загружается.

Электронный конспект лекций
по курсу
«Математическая логика
и теория алгоритмов»
Введение
Данный материал предназначен для студентов 2-го курса, изучающих
математическую логику и теорию алгоритмов. Семестровый курс "Математическая
логика и теория алгоритмов" является непосредственным продолжением курса
дискретной математики.
Основы математической логики и теории алгоритмов, излагаемые в конспекте,
могут использоваться при изучении ряда профилирующих дисциплин для подготовки
специалистов по информатике, вычислительной технике, прикладной математике,
автоматике и автоматизированному управлению. К таким дисциплинам относятся
бакалаврские дисциплины "Базы данных", "Системы искусственного интеллекта",
"Логическое программирование", "Структуры и алгоритмы обработки данных",
'Теория автоматов", "Теория вычислительных процессов", и др.
1

Содержание.
1. ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ..............................................................................3
1.1. Определение формального исчисления...................................................................3
1.2. Исчисление высказываний генценовского типа.....................................................4
1.3. Эквивалентность формул........................................................................................11
1.4. Нормальные формы.................................................................................................14
1.5. Семантика исчисления секвенций..........................................................................16
1.6. Исчисление высказываний гильбертовского типа................................................20
1.7.
Алгоритмы проверки общезначимости и противоречивости в ИВ
...........23
2. ЛОГИКА И ИСЧИСЛЕНИЯ ПРЕДИКАТОВ............................................................30
2.1.
Алгебраические системы.
Формулы сигнатуры Σ. Истинность формулы на
алгебраической системе
................................................................................................31
2.2.
Секвенциальное исчисление предикатов
........................................................37
2.3.
Эквивалентность формул в
ИПС
................................................................46
2.4.
Нормальные формы
..........................................................................................47
2.5. Теорема о существовании модели..........................................................................49
2.6.
Исчисление предикатов гильбертовского типа
ИП
...................................50
2.7. Скулемизация алгебраических систем..................................................................52
2.8. Метод резолюций в исчислении предикатов........................................................54
2.9. Некоторые проблемы аксиоматического исчисления предикатов
.........61
3. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ......................................................................63
3.1. Машины Тьюринга
...........................................................................................65
3.2. Функции, вычислимые на машинах Тьюринга.
.....................................67
3.3. Рекурсивные функции и отношения......................................................................69
3.4. Неразрешимость исчисления предикатов. Теорема Геделя о неполноте.
Разрешимые и неразрешимые теории...............................................................................75
1. ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ
1.1. Определение формального исчисления
Введем общее понятие формального исчисления. Будем говорить, что
формальное исчисление I определено, если выполняются следующие четыре условия:
2

1. Имеется некоторое множество А(I) ― алфавит исчисления I. Элементы
алфавита А(I) называются символами. Конечные последовательности символов
называются словами исчисления I. Обозначим через W(I) множество всех слов
алфавита исчисления I.
2. Задано подмножество Е(I)
W(I), называемое множеством выражений
исчисления I. Элементы множества Е(I) называются формулами или секвенциями.
3. Выделено множество А
х
(I)
Е(I) выражений исчисления I, называемых
аксиомами исчисления I.
4. Имеется конечное множество (I) частичных операций R
1
R
2
, ..., R
n
на
множестве Е(I), называемых правилами вывода исчисления I.
Итак, исчисление I есть четверка <A(I),E(I), A
x
(I), (I)>.
Если
n
XYXYf :
, то f будем называть частичной n-местной операцией на X с
областью определения Y.
Если набор выражений (Φ
1
,...,Ф
m
, Ф) принадлежит правилу R
i
то выражения
Φ
1
,...,Ф
m
называются посылками, а выражение Φ ― непосредственным следствием
выражений Φ
1
,...,Ф
m
по правилу R
i
, или заключением правила R
i
. Записываться этот
факт будет следующим образом:
i
m
,...,
1
Иногда в этой записи символ i будем опускать, если ясно, о каком правиле идет
речь:
m
,...,
1
Выводом в исчислении I называется последовательность выражений Φ
1
, Ф
2
, ..., Ф
N
такая, что для любого i (1<= i<=n) выражение Ф
i
, есть либо аксиома исчисления I, либо
непосредственное следствие каких-либо предыдущих выражений.
Выражение Φ называется теоремой исчисления I, выводимым в I или доказуемым
в I. если существует вывод Φ
1
,...,Ф
n
,Ф, который называется выводом выражения Φ или
доказательством теоремы Ф
П р и м е р 1. Пусть Е(I) — множество повествовательных предложений русскою
языка, А
х
(I) множество истинных в данный момент времени предложений вида
"подлежащее сказуемое" с точкой на конце. Имея правила вывода
3

.
..;
и
и
.
..;
или
можно из простых предложений (аксиом) составлять более сложные (теоремы),
также истинные в данный момент времени.
Вообще говоря, может не существовать алгоритма, с помощью которого для
произвольного выражения Φ формального исчисления I за конечное число шагов
можно определить, является ли Φ выводимым в I или нет. Если такой алгоритм
существует, то исчисление называется разрешимыми, а если такого алгоритма нет ―
неразрешимым. Исчисление называется непротиворечивым, если не все его
выражения доказуемы.
Ниже мы проведем построение двух формальных исчислений - исчислений
высказываний, в основе которых лежат формулы алгебры логики. Первое из этих
исчислений ― исчисление высказываний генценовского типа, предложенное
Генценом, в качестве выражений использует секвенции, построенные из формул
алгебры логики. Это исчисление будет обозначаться через ИС. Второе исчисление -
исчисление высказываний гильбертовского типа, создано Гильбертом, и в нем
выражениями являются непосредственно формулы алгебры логики. Исчисление
высказываний гильбертовского типа будет обозначаться через ИВ. Мы покажем, что
оба исчисления эквивалентны в том смысле, что доказуемыми в них будут являться в
точности тождественно истинные формулы. Из последнего факта будут вытекать
разрешимость и непротиворечивость исчислений высказываний.
Строящиеся в дальнейшем исчисления ИПС и ИП, являющиеся расширениями
исчислений ИС и ИВ соответственно, послужат примерами неразрешимых
непротиворечивых исчислений.
1.2. Исчисление высказываний генценовского типа
Определим элементы исчисления высказываний ИС.
Алфавит ИС состоит из букв А, В, Q, Р, R и других, возможно, с индексами
(которые называются пропозициональными переменными), логических символов
(связок) отрицания , конъюнкции , дизъюнкции , импликации →, следования ├·, а
также вспомогательных символов: левой скобки (, правой скобки ), запятой ,.
4

Множество формул ИС определяется индуктивно: Слово алфавита ИС называеся
формулой, если:
a) все пропозициональные переменные являются формулами ИС (такие
формулы называются элементарными или атомарными)
b) если φ, ψ — формулы ИС, то φ, (φ
ψ), (φ
ψ), (φ→ψ) - формулы ИС;
c) выражение является формулой ИС тогда и только тогда когда это может
быть установлено с помощью пунктов "а" и "б"
В дальнейшем при записи формул будем опускать некоторые скобки, используя
те же соглашения, что и в алгебре логики.
Определение. Подформулой ψ формулы φ ИС будем называть подслово φ,
являющееся формулой ИС.
Если все вхождения подформулы ψ в φ заменить на формулу
, то получим новую
формулу
)(
.
Предложение 1. Каждая неатомарная формула
в ИС представима в одном и только
одном из следующих видов
)(),(),(,
для однозначно определенных
и
.
Секвенциями называются конечные выражения следующих: двух видов, где φ
1
,
…,φ
n
, ψ ― формулы ИС:
φ
1
,…,φ
n
├ψ (говорится "из истинности φ
1
,…,φ
n
логически следует ψ”),
φ
1
,…,φ
n├
(говорится "система формул φ
1
,…,φ
n
противоречива")
Последовательности формул φ
1
,…,φ
n
в секвенциях будут часто обозначаться
через Г (возможно, с индексами): Г├ψ, Г├ .При этом последовательность Г считается
пустой при n=0. Значит, записи ├ψ и ├ также являются секвенциями, первая которых
может читаться как утверждение о доказуемости формулы ψ.
Таким образом, наряду с формулами, символизирующими простые или сложные
высказывания, секвенции являются записями утверждений, в которых выделяются
посылки и заключение. Буквы
,
,
будем называть переменными для формул;
добавим их к алфивиту ИС и обозначим через В.
Определение. Схемой секвенций (формул) ИС будем называть такое слово в
алфавите В, что при любой подстановке в это слово вместо переменных формул
соответствующих конкретных формул, получим секвенцию (формулу) ИС. Результат
5
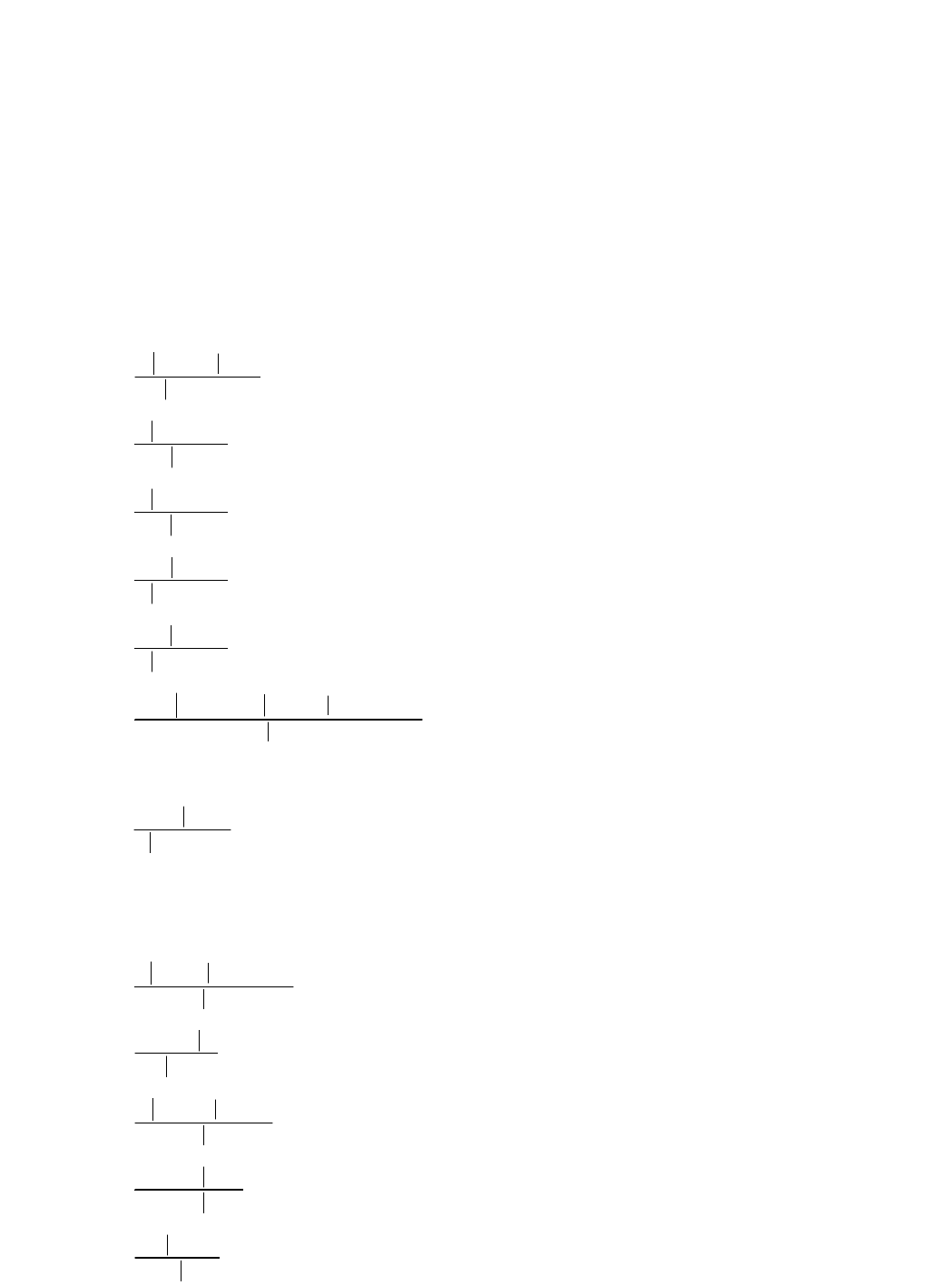
подстановки будем называть частичным случаем этой схемы.
Пример.
|,
- схема,
)()(|,
- результат подстановки,
где
)(,,
.
Множество аксиом ИС определяется следующей схемой секвенций. φ├φ, где φ
― произвольная формула ИС.
Аксиомами являются, например, секвенции Α→
A→B
C├ Α→
A→B
C.
Правилa вывода ИС (формализуют стандартные логические способы
рассуждений) задаются следующими записями, где Г — произвольная (возможно пустая)
конечная последовательности формул ИС, φ,ψ,χ — произвольные формулы ИС.
1.
;
(введение Λ).
2.
(удаление ).
3.
(удаление ).
4.
(введение ).
5.
(введение ).
6.
)(;,;,
(удаление , или правило разбора двух
случаев).
7.
,
(введение →) – правило эквивалентной
переформулировки теорем. Когда условие теоремы перемещается в
заклячение в виде посылки.
8.
;
(удаление →) – правило отделения, modus ponens.
9.
,
(удаление , или доказательство от противного).
10.
;
(выведение или обнаружения противоречия)
11.
,,
,,
(перестановка посылок).
12.
,
(утончение, или правило лишней посылки) –
добавление условий не влияет на вывод.
6

Вывод S
0
,.. S
n
, - в ИС называется линейным доказательством. Секвенция S
называется доказуемой в ИС, или теоремой ИС, если существует линейное
доказательство So,..,Sn в ИС, заканчивающееся секвенцией S: S
n
= S Формула φ
называется доказуемой в ИС, если в ИС доказуема секвенция ├φ . Если
n
SS ,...,
0
-
доказательство в ИС,
k
SS
,...,
0
- также, тогда
n
SS ,...,
0
,
k
SS
,...,
0
- тоже доказательство
ИС.
Определим по индукции понятие дерева секвенций:
1) любая секвенция является деревом секвенций;
2) если D
o
, …,D
n
— деревья секвенций и S — секвенция, то запись
S
DD
n
;...;
0
также является деревом секвенций;
3) любое дерево секвенций строится в соответствии с пп. 1 и 2.
Вхождением секвенции в дерево D называется место, которое секвенция занимает в
дереве. Каждая секвенция может иметь несколько вхождений в дерево секвенций.
Вхождение секвенции дерево D, над (под) которым нет горизонтальной черты,
называется начальным (соответственно заключительным).
Из определения дерева секвенций ясно, что начальных секвенций в дереве
может быть несколько, а заключительная секвенция единственна.
Часть дерева, состоящая из секвенций, находящихся непосредственно над
некоторой чертой, под той же чертой, а также самой черты, называется
переходом.
Дерево D называется доказательством в ИС в виде дерева, если все его
начальные секвенции суть аксиомы ИС, а переходы осуществляются по правилам
1-12. Дерево D называется доказательством секвенции S в виде дерева в ИС, или
деревом вывода S в ИС, если D — доказательство в ИС и S — его заключительная
секвенция.
Покажем, что наличие линейного доказательства секвенции равносильно
существованию доказательства секвенции в виде дерева.
Предложение 1. Секвенция S имеет доказательство в ИС в виде дерева
тогда и только тогда, когда S ― теорема ИС.
Доказательство. Пусть S
0
,..., S
n-1
, S ― линейное доказательство в ИС. Если
7
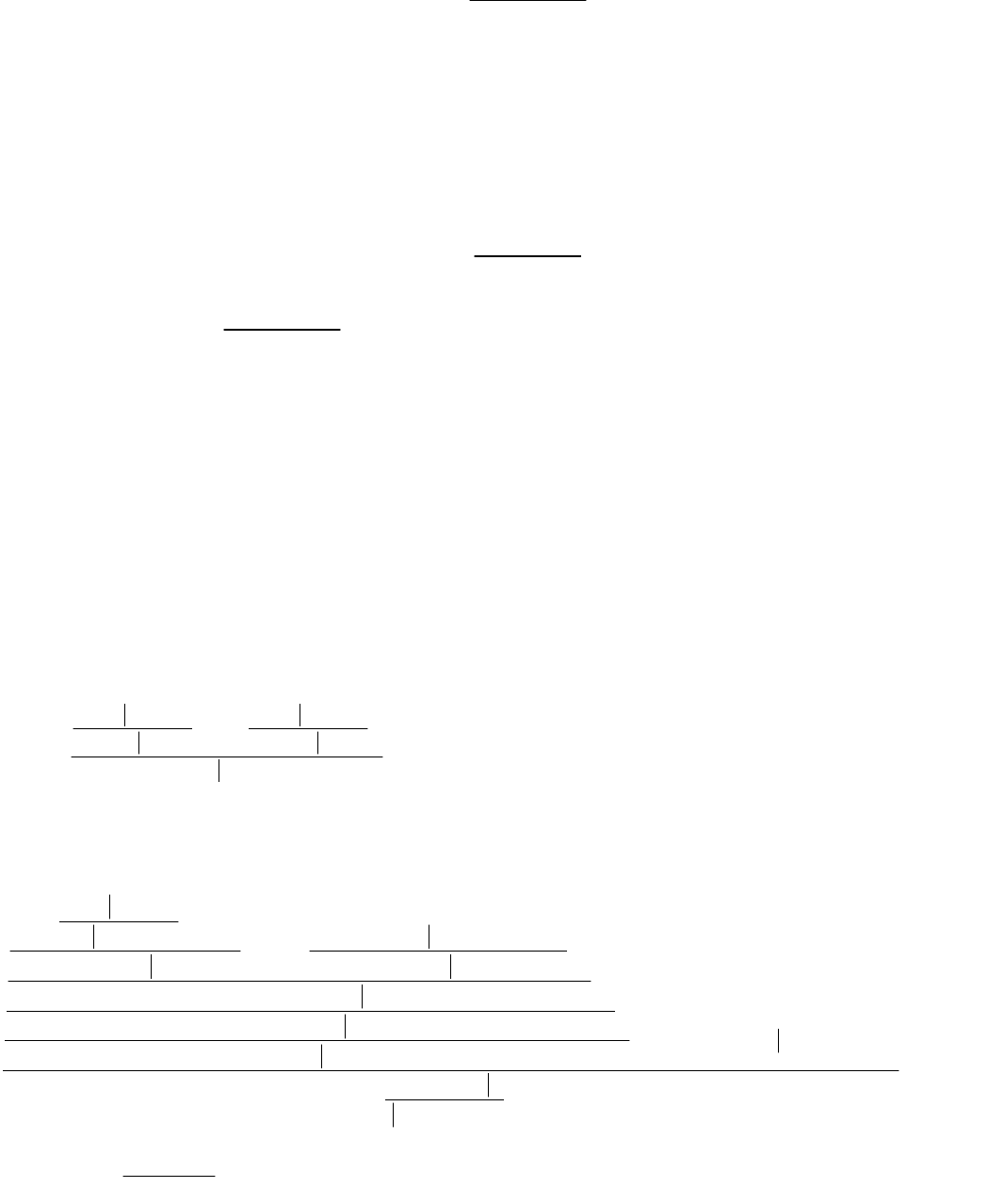
S ― аксиома, то S ― доказательство секвенции S в виде дерева. Предполагая по
индукции, что секвенции S
0
,..., S
n-1
имеют доказательства D
0
,..., D
n-1
в виде
дерева, а секвенция S получается из секвенций S
i1
,..., S
ik
применением
некоторого правила вывода, заключаем, что дерево
S
DD
iki
;...;
1
является доказательством секвенции S в виде дерева.
Пусть теперь дано доказательство секвенции S в виде дерева D. Если S ―
аксиома, то S является линейным доказательством секвенции S. Допустим, что
секвенция S не является аксиомой. Тогда дерево D имеет вид
S
DD
n
;...;
0
где D
i
=S
i
или
S
DD
iki
;...;
1
,
i = 0,...,п. Предполагая по индукции, что секвенции Si имеют линейные
доказательства L
i
, i= 0,...,п, получаем линейное доказательство L
0
, ..., L
n
, S
секвенции S.
Очевидно, что представление доказательства в виде дерева более наглядно и
позволяет проследить все переходы по правилам вывода.
П р и м е р 1 . Приведем доказательство секвенций φ
ψ├ψ
φ в виде дерева
для любых формул φ и ψ.
1
23
;
2. Следующее дерево демонстрирует доказуемость формулы φ
φдля любой
формулы φ:
10
9
)(
)(
)()(4
;)(
9
)(
10
),(
12
)(),(
)()(
12,11
),(
5
Правило
S
SS
n
,...,
0
называется допустимым в ИС, если из выводимости в ИС
8

секвенций S
0
,..., S
n
следует выводимость в ИС секвенции S.
Заметим, что допустимость правила равносильна тому, что его добавление в
исчисление ИС не расширяет множество доказуемых секвенций.
Предложение 2. Следующие правила допустимы в ИС:
(а)
n
m
,...,
,...,
1
1
(расширение посылок);
(б)
n
m
,...,
,...,
1
1
(расширение посылок);
где в пп. (а) и (б) выполняется
},...,{},...,{
11 nm
(в)
Г
ГГ ,;
(сечение);
(г)
,
,,
Г
Г
(объединение посылок);
(д)
,,
,
Г
Г
(расщепление посылок);
(е)
,
,;,
Г
ГГ
(разбор случаев)
(ж)
Г
Г
(выведение противоречия)
(з)
Г
Г
(выведение из противоречия)
(и)
Г
Г,
(контрапозиция);
(к)
,Г
Г
(контрапозиция);
(л)
,
,
Г
Г
(контрапозиция);
(м)
,
,
Г
Г
(доказательство от противного);
(н)
)...(
,...,
0
0
n
n
(введение
, →);
(о)
n
n
,...,
)...(
0
0
(удаление
, →)
Доказательство. Допустимость правила
,
,,
показывается следующим деревом:
9
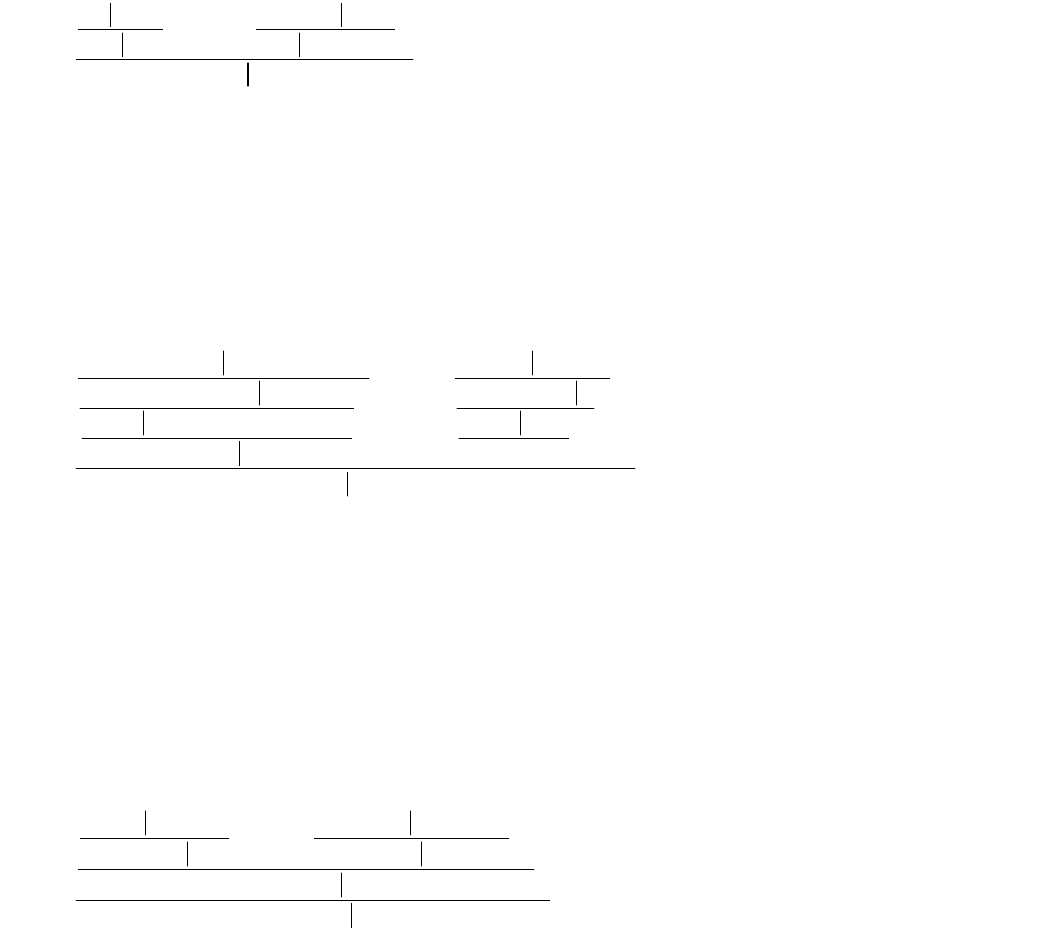
8
,
7
,
,,
12,11
;,
Допустимость правила (а) следует из допустимости указанного правила с
помощью правил 11 и 12. Допустимость правила (б) вытекает из правил (а), (ж) и
(з).
Докажем допустимость правила (з), а остальные правила оставим студентам
в качестве упражнения
9
12
9
10
,
,,
12,12
9
,
;,
,,
устанавливает доказуемость секвенции Г├φ.
Использование допустимых правил вывода позволяет во многих случаях
приводить сокращенные доказательства секвенций, которые при необходимости
можно преобразовать в доказательства секвенций в виде деревьев в ИС.
Например, следующее дерево устанавливает доказуемость се
квенции
(φ→ψ),
ψ├
φ:
л
),(
8
),(
12
),(
)(
11,12
;),(
Правило называется равносильным, если доказуемость (единственной)
секвенции, стоящей над чертой, равносильна доказуемости секвенции, стоящей под
чертой. Из предложения 1.2.2 вытекает, что следующие правила равносильны: 9, 11,
(г), (д), (ж), (и), (к), (л), (м), (н), (о).
1.3. Эквивалентность формул
Пусть V ― {Р
i
| i
ω} ― множество всех пропозициональных переменных ИС, F
― множество всех формул ИС. Любая функция s : V → F называется подстановкой
пропозициональных переменных. Для любой формулы φ
F обозначим через s(φ)
формулу, получающуюся из φ заменой всех пропозициональных переменных Р,
входящих в φ, на формулы s(P), при этом справедливы следующие свойства:
1. s(φ)=s(φ)
10
