Основы математической логики и теории алгоритмов
Подождите немного. Документ загружается.


1. Предикатные и функциональные символы, образующие сигнатуру Σ.
2. Символы переменных, составляющих множество V.
3. Символ равенства: .
4. Логические связки: ¬, , ,
.
5. Кванторы: ,.
6. Вспомогательные символы: левая скобка (, правая скобка), запятая ,.
Термы сигнатуры
определим по индукции:
1. переменные xV являются термами
2. если t
1
,...t
n
– термы , f
F,
(f)=n, то f(t
1
,...t
n
) – терм (при n=0 константа с
– тоже терм).
Пример.
=<c, g
(2)
, h
(2)
>, g,h –функции. x, y,V, тогда термами являются с, x, y,
g(c,x), h(c,c), g(y,h(c,c)),h(y,c), h(g(c,x),h(y,c)).
Обозначим через Τ(Σ) множество всех термов сигнатуры Σ, в определении
которых используются лишь переменные из V. Очевидно, любой терм из Τ(Σ)
является словом алфавита ИΠ
Σ
.
Введем понятие атомарной формулы сигнатуры Σ:
1) если t
1
, t
2
Τ(Σ), то (t
1
t
1
) — атомарная формула;
2) если р
(n)
Σ — предикатный символ, t
1
,...t
n
Τ(Σ), тο p(t
1
,...t
n
) —
атомарная формула;
3) никаких атомарных формул, кроме построенных по пп. 1, 2, нет.
Формула сигнатуры Σ определяется следующим образом:
1) атомарная формула есть формула;
1) если φ, ψ — формулы и xV, то ¬ψ, (ψ φ), (ψ φ),(φ
ψ), x φ,
xφ —
формулы;
2) никаких формул, кроме построенных по пп. 1, 2, нет.
Символы , , использованные в определении, называются соответственно
квантором всеобщности и квантором существования. Запись x (соответственно
х) читается "для всех х" ("существует х"). Все соглашения относительно
расстановок скобок, принятые ранее, остаются в силе и для формул логики
предикатов. Кроме того, вместо записей x
1
...x
n
φ и х
1
... х
n
φ будем
использовать записи x
1
,...,x
n
φ и х
1,
... ,х
n
φ. Формула φ сигнатуры Σ называется
бескванторной, если она не содержит кванторов.
31

П р и м е р 1. Рассмотрим предикатную сигнатуру Σ=<Q
(1)
,R
(1)
,P
(1)
,
меньше
(2)
> со следующими интерпретациями:
Q(x) – X - рациональное число,
R(x) - x — вещественное число,
Р(х) - x — простое число,
меньше(х, у) х < у.
Формула
x (Q(x)
R(x)) означает, что любое рациональное число является
вещественным, а формула
x
y (меньше(х, у)
Ρ (у)) – для любого элемента х
найдется больший элемент у, являющийся простым числом.
2. Любая бескванторная формула сигнатуры нульместных предикатов
может рассматриваться как формула исчисления высказываний. Например, таковой
является формула АВ ¬С сигнатуры Σ = {А
(0)
, В
(0)
, С
(0)
}.
Определим множество SF(φ) подформул формулы φ сигнатуры Σ:
1) если φ — атомарная формула, то φ — ее единственная подформула и
SF(φ) = {φ};
2) если φ имеет вид ¬φ
1
, или x φ
1
, или х φ
1
, то подформула формулы φ
— это либо φ, либо подформула формулы φ
1
и SF(φ)=SF(φ
1
){φ}.
3) если φ имеет вид φ
1
φ
2
, или φ
1
φ
2
, или φ
1
φ
2
, то подформула формулы φ —
это либо φ, либо подформула формулы φ
1
, либо подформула формулы φ
2
и SF(φ) =
SF(φ
1
) SF(φ
2
) {φ}·
Каждое вхождение квантора () в данную формулу φ однозначно
определяет некоторое вхождение
хψ (
хψ) подформулы из SF(φ), первым символом
которого является рассматриваемое вхождение соответствующего квантора. Формула
хψ(
хψ), связанная с вхождением квантора (), называется областью действия этого
вхождения квантора.
Заметим, что в записи формулы возможно наложение области действия вхождения
одного квантора с данной переменной на область действия другого квантора с той же
самой переменной. Например, в формуле
х(Р
2
(х,у)
xΡ
1
(x)) вхождение переменной x
в Р
1
(х) находится одновременно под кванторами x и x. Поскольку число переменных,
образующих множество V, бесконечно, мы будем избегать подобных коллизий введением
новых переменных для меньших областей действия вхождений кванторов. Так, вместо
формулы
х(Р
2
(х,у)
xΡ
1
(x)) будет рассматриваться, например, формула
х(Р
2
(х,у)
32

zΡ
1
(z)).
Говорят, что вхождение переменной x в формулу φ связано в φ, если оно находится
в области действия некоторого вхождения квантора в формулу φ, имеющую вид x ψ или
х ψ; в противном случае это вхождение называется свободным в φ. Переменная x
называется свободной (связанной), если некоторое вхождение x в φ свободно (связано).
П р и м е р 3. Рассмотрим следующие формулы сигнатуры S={P
1
(1)
, P
2
(2)
}:
¬ P
1
(x); P
2
(x,y)x P
1
(x); x(P
2
(x,y)P
1
(x))
Переменная х в первой формуле является свободной, во второй — и свободной, и
связанной, в третьей — связанной; переменная у во всех формулах свободна.
Предложением или замкнутой формулой сигнатуры Σ называется формула
сигнатуры Σ, не имеющая свободных переменных.
П р и м е р 4. Формула x,y(x + у у + х) является предложением сигнатуры
{+}, формула
z
х (
у Р
2
(х,у)
¬Ρ
1
(x)) — предложением сигнатуры <{ P
1
(1)
, P
2
(2
}> а
формула x (Р
2
(х,у)
¬Ρ
1
(x)) предложением не является.
Запись φ(x
1
,..,x
n
) будет означать, что все свободные переменные формулы φ
содержатся в множестве {x
1
,..,x
n
}.
Дадим индуктивное определение истинности формулы φ(x
1
,..,x
n
) сигнатуры Σ
на элементах a
1
,..,a
n
А в алгебраической системе A = (Α;Σ) (запись A╞ φ(a
1
,..,a
n
)
будет означать, что формула φ истинна на элементах a
1
,..,a
n
А в системе A):
1) если t
1
, t
2
Τ(Σ), то A |= t
1
( a
1
,..,a
n
)
t
2
(a
1
,..,a
n
) значения термов t
1
, t
2
в системе A на элементах a
1
,..,a
n
A совпадают;
2) если p
(k)
— предикатный символ сигнатуры Σ, t
1
,...t
k
T(Σ), то
A╞P(t
1
(a
1
,..,a
n
),..., t
k
(a
1
,..,a
n
)) -- <t
1
(a
1
,..,a
n
),..., t
k
(a
1
,..,a
n
)>P
A
;
1) A |= (ψ(a
1
,..,a
n
)χ(a
1
,..,a
n
)) A |= ψ(a
1
,..,a
n
) и A |= χ(a
1
,..,a
n
)
2) A |= (ψ(a
1
,..,a
n
)χ(a
1
,..,a
n
)) A |= ψ(a
1
,..,a
n
) или A |= χ(a
1
,..,a
n
)
3) A |= (ψ(a
1
,..,a
n
)χ(a
1
,..,a
n
)) если A |= ψ(a
1
,..,a
n
), то A |= χ(a
1
,..,a
n
)
4) A |= ¬ψ(a
1
,..,a
n
) неверно, что A |= ψ(a
1
,..,a
n
)
5) A |=xψ(x,a
1
,..,a
n
) A |= ψ(a,a
1
,..,a
n
) для aA
6) A |=xψ(x,a
1
,..,a
n
) A |= ψ(a,a
1
,..,a
n
) для некоторого aA
33

Если не выполняется A|=φ(a
1
,..,a
n
), то будем говорить, что формула φ ложна
на элементах a
1
,..,a
n
в системе A, и писать A
|
φ(a
1
,..,a
n
)
П р и м е р 1. Записать формулу φ(x), истинную в A=<
; +
(2)
,
(2)
> тогда и
только тогда, когда x четно.
Искомая формула φ(x) имеет, например, вид
y (х у + у).
П р и м е р 2.. Рассмотрим формулу φ(x, у) функциональной сигнатуры {+
(2),
0
(0)
},
имеющую вид (х + у 0). Для алгебраической системы A = <Z; +, 0> тогда и только тогда
имеет место A╞φ(m, n), когда т = —n. Для формулы ψ(х)=
у (х+у 0) справедливо A╞
ψ(п) для любого целого числа n, поскольку у любого целого числа имеется к нему
противоположное и так же целое число. Следовательно, A╞xy(x +y
0).
Формула φ(x
1
,..,x
n
) сигнатуры Σ называется тождественно истинной или
общезначимой (тождественно ложной или противоречивой), если для любой
алгебраической системы A = <Α; Σ> и любого кортежа элементов (a
1
,..., а
п
) А
п
выполнено A╞φ(a
1
,..., а
п
) (A
|
φ(a
1
,..., а
п
))· Если φ — тождественно истинное
предложение, то пишем ╞ φ.
Формула φ(x
1
,..,x
n
) называется выполнимой в системе A, если A╞φ(a
1
,..., а
п
) для
некоторых a
1
,..., а
п
А.
П р и м е р 1. Формула (х х) общезначима, поскольку A╞(а а) для любой
системы A = <A; Σ> и любого элемента a
А По этой же причине формула ¬(x х)
тождественно ложна.
П р и м е р 2. Формула φ= x, у (х · у у · x) выполнима, но не тождественно
истинна, так как <Z; > |= φ, а на АС =<Μ
2
(Ζ); ·> не выполняется, где Μ
2
(Ζ) —множество
матриц порядка 2 с элементами из Ζ.
П р и м е р 3 . φ=xy(x +y
0) - выполнима, но не тождественно истинна, так
как <Z; +,0> |= φ, <N;+,0>
|
φ. Т.е. предложение φ описывает свойство, отличающие
системы друг от друга.
Предложение 1.
1. Для любой формулы φ сигнатуры Σ следующие формулы общезначимы:
(а) x ¬φ ¬x φ;
(б) х ¬φ ¬x φ;
34

(в) x,y φ
y,xφ;
(г) х,уφ у,хφ;
(д) xy φ
yx φ.
2. Для любой формулы φ сигнатуры Σ формула x φ х¬φ противоречива. .
Заметим, что общезначимость формулы yx φ xy φ в общем случае
утверждать нельзя.
Следующая теорема позволяет создавать общезначимые и противоречивые
формулы на основе формул ИВ.
Теорема 1. Пусть φ(Α
1
,..., А
п
) — общезначимая (противоречивая) формула ИВ,
φ
1
,..., φ
n
— формулы сигнатуры Σ. Тогда в результате подстановки формул φ
1
,..., φ
n
вместо всех соответствующих вхождений пропозициональных переменных Α
1
,..., А
п
образуется общезначимая (противоречивая) формула φ(φ
1
,..., φ
n
) сигнатуры Σ.
Доказательство. Нетрудно заметить, что если φ(Α
1
,..., А
п
) — общезначимая
(противоречивая) формула ИВ, то при любых значениях истинности формул φ
1
,..., φ
n
на элементах алгебраической системы формула φ(φ
1
,..., φ
n
) будет истинной (ложной) на
тех же элементах.
Теорема 2. Если f — изоморфизм системы A на систему A, φ(x
1
,... ,х
п
) —
формула сигнатуры системы A, то для любых a
1
,..., а
п
А свойство A╞φ(a
1
,..., а
п
)
эквивалентно свойству A╞ φ(f(а
1
),..., f(а
n
)).
Доказательство легко проводится индукцией по числу шагов построения
формулы φ. При этом для атомарной формулы φ утверждение следует
непосредственно из определения изоморфизма.
Множество формул Г сигнатуры Σ с множеством свободных переменных X
называется выполнимым, если существует система M = <Μ; Σ>, элементы а
х
Μ для
каждого x
X такие, что для любой формулы φ(x
1
,... ,х
п
) Γ выполнимо M ╞
φ(а
x1
,... ,а
xп
). Система M называется моделью множества формул Г, и этот факт
обозначается через M ╞Г.
Пример. Рассмотрим следующее множество формул сигнатуры {},
описывающих линейные порядки: Γ
lo
= {
х (х
x),
x,y,z(((x
у)
(у
z)) (x
z)),
x,y(((x
у) (у
х))
(хy)),x,y((x у) (у
х))}· Очевидно, что множество Γ
lo
имеет как конечные, так и бесконечные модели. Например, <{0}; > ╞ Г
1о
, где {0} =
35

{(0,0)}, а на <Ν; > ╞ Г
lo
. Добавив к множеству Г
1о
две формулы х, у ¬(х у) и
х,
у((х
у)
¬ (х у) z((x
z)
¬(x z) (z у)¬(z у))), получаем множество Г
dlo,
описывающее бесконечные плотные линейные порядки. Моделями множества Г
dlo
являются в точности бесконечные линейно упорядоченные множества, у которых
между любыми двумя различными элементами имеется некоторый промежуточный.
Примерами таких моделей служат <Q; > и <R; >.
2.2. Секвенциальное исчисление предикатов
Зафиксируем некоторую произвольную сигнатуру Σ и определим
секвенциальное исчисление предикатов сигнатуры Σ (ИПС
).
Алфавит ИПС
получается из алфавита ИΠ
Σ
добавлением символа следования ├,
т.е. Α(ИΠС
Σ
) = Σ V {,¬,,, , , , (,),,, ├}. Формулами ИПС
будут формулы
сигнатуры Σ.
Секвенциями ИПС
называются конечные последовательности следующих двух
видов, где φ
1
,...,φ
n
,φ — формулы ИПС
:
φ
1
,…,φ
n
├φ
φ
1
,…,φ
n├
.
Примем следующие соглашения. Пусть x
1
,... ,х
n
— переменные, t
1
,...,t
n
— термы
сигнатуры Σ и φ — формула сигнатуры Σ. Запись
n
n
xx
tt
,...,
,..,
1
1
)(
будет обозначать результат
одновременной подстановки термов t
1
,...,t
n
вместо всех свободных вхождений в φ
переменных x
1
,... ,х
n
соответственно, причем, если в тексте встречается запись
n
n
xx
tt
,...,
,..,
1
1
)(
, то предполагается, что для всех i = 1,..,n ни одно свободное вхождение в φ
переменной x
i
не входит в подформулу φ вида
yφ
1
или
yφ
1
, где у — переменная,
входящая в t
i
. Вместо записи
n
n
xx
tt
,...,
,..,
1
1
)(
будем иногда писать φ( t
1
,...,t
n
). При этом, наряду
с тем, что переменные x
1
,... ,х
n
в записи φ(x
1
,... ,х
n
) будут всегда предполагаться
попарно различными, среди t
1
,...,t
n
могут быть равные термы.
Пример . 1. Обозначим через φ формулу
х R(x, у, z), через t
1
— терм F
1
(y,z,u),
через t
2
— терм F
2
(F
3
(z), w). Результат подстановки
zy
tt
,
,
21
)(
равен
xR(x, F
1
(y,z,u),F
2
(F
3
(z),w)), a результат подстановки
zy
tt
,
,
11
)(
равен
х R(x, F
1
(y,z,u), F
1
(y,z,u)).
36
Заметим, что результат последовательной подстановки может не совпадать с
результатом одновременной подстановки.
2. Для формулы φ =
х R(x, у, z) и терма t = F(y, x, и) запись (φ)
t
y
недопустима, поскольку после подстановки терма t вместо свободной переменной
у в формуле
хR(x,F(y,x,u),z) вхождение переменной x в терм t становится
связанным.
Аксиомами ИПС
являются следующие секвенции:
1) φ├φ, где φ — формула сигнатуры Σ;
2) ├(xx), где x— переменная;
3)
(t
1
q
1
) , . . . , ( t
n
q
n
),
n
n
xx
tt
,...,
,..,
1
1
)(
├
n
n
xx
qq
,...,
,..,
1
1
)(
где t
1
,...,t
n
, q
1
,...,q
n
— термы сигнатуры Σ, φ — формула, удовлетворяющая
условиям на записи
n
n
xx
tt
,...,
,..,
1
1
)(
и
n
n
xx
qq
,...,
,..,
1
1
)(
Правила вывода ИПС
задаются следующими записями, где Г —
произвольные (возможно пустые) конечные последовательности формул ИΠС
Σ
, φ,
ψ, χ — произвольные формулы ИПС
:
1.
;
(введение Λ).
2.
(удаление ).
3.
(удаление ).
4.
(введение ).
5.
(введение ).
6.
)(;,;,
(удаление , или правило разбора двух случаев).
7.
,
(введение →).
8.
;
(удаление →).
9.
,
(удаление , или доказательство от противного).
10.
;
(выведение противоречия)
37
11.
,,
,,
(перестановка посылок).
12.
,
(утончение, или правило лишней посылки).
13.
x
где переменная х не входит свободно в формулы из Г
(введение справа)
14.
x
x
t
,
)(,
(введение слева)
15.
x
x
t
)(
(введение справа)
16.
x,
,
где переменная х не входит свободно в ψ и в формулы из
Г (введение слева)
Понятия линейного доказательства в ИПС
, доказательства в виде дерева в ИПС,
доказуемой в ИПС секвенции (теоремы ИПС
) и доказуемой в ИПС
формулы
определяются аналогично соответствующим понятиям ИС на основе аксиом 1-3 и
правил вывода 1-16. Также аналогично предложению 1.2.1 устанавливается
Предложение 1. Секвенция S имеет доказательство в ИПС
в виде дерева
тогда и только тогда, когда S — теорема ИПС
.
Пример. Приведем доказательство секвенции х
yφ(x,y)├
y
хφ(х,у) в виде
дерева для любой формулы φ(х,у):
15
14
13
16
),(),(
),(),(
),(),(
),(),(
),(),(
yxxyyxyx
yxxyyxy
yxxyxy
yxxyx
yxyx
Следующая теорема является синтаксическим аналогом теоремы 2.1.2 и
позволяет преобразовывать доказуемые формулы ИС в доказуемые формулы ИПС
.
Теорема 2. Пусть φ(Α
ι
,..., Α
n
) — доказуемая формула ИС, φ
1
,...,φ
n
— формулы
сигнатуры Σ. Тогда в результате подстановки формул φ
1
,...,φ
n
вместо всех
соответствующих вхождений пропозициональных переменных Α
ι
,..., Α
n
образуется
доказуемая в ИПС
формула φ(φ
1
,...,φ
n
).
Доказательство. Пусть D — дерево доказательства секвенции ├ φ (Α
ι
,..., Α
n
) в
ИС. Тогда, заменяя в дереве D переменные Α
ι
,..., Α
n
соответственно на φ
1
,...,φ
n
, а
38
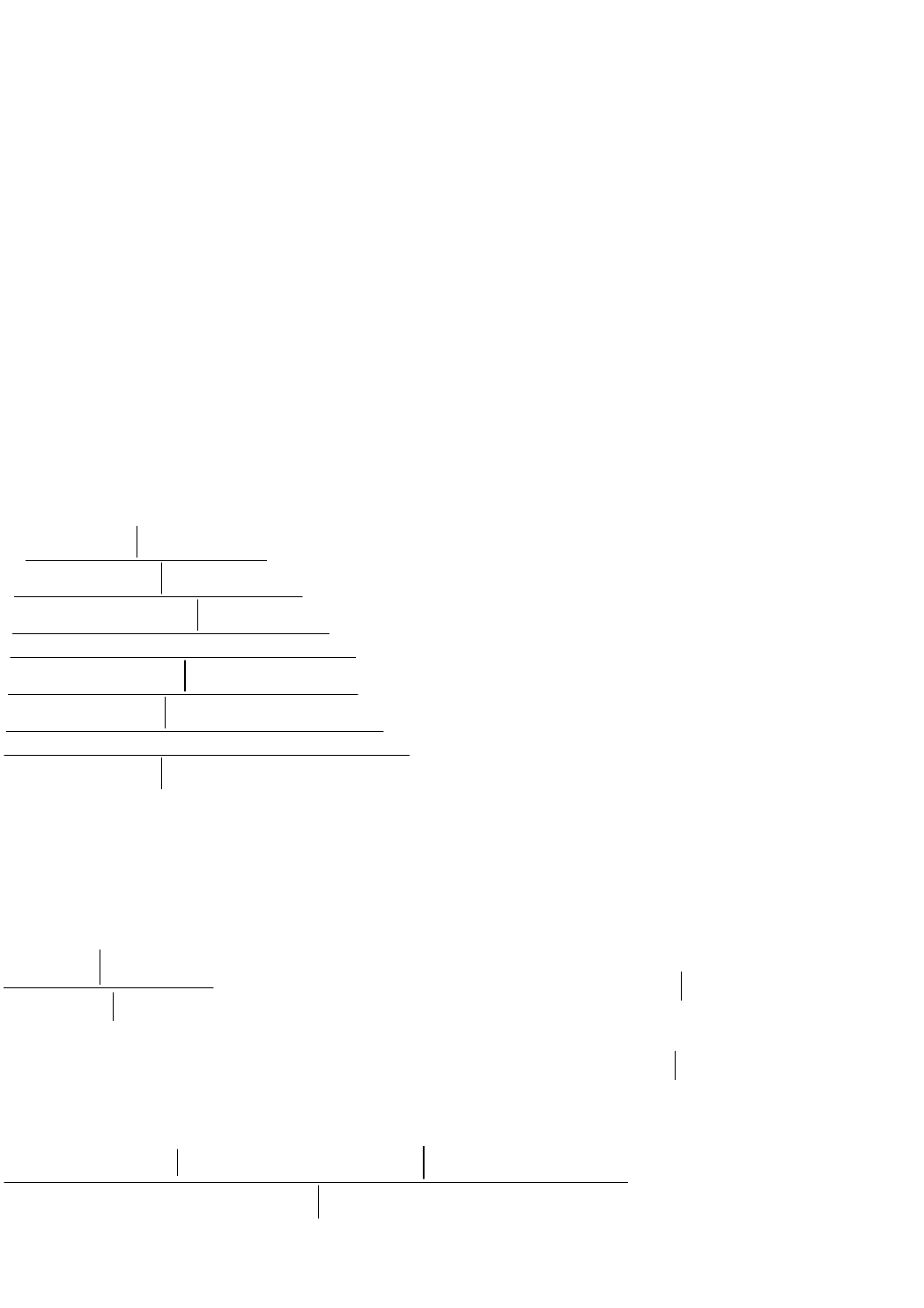
остальные пропозициональные переменные — на формулу (x
х), получаем дерево D
1
,
являющееся деревом доказательства секвенции ├ φ(φ
1
,...,φ
n
).
Предложение 3. Для любой формулы φ, удовлетворяющей условиям на запись
n
n
xx
tt
,...,
,..,
1
1
)(
, в ИПС
доказуемы следующие секвенции:
a)
x
1
,…,x
n
├
n
n
xx
tt
,...,
,..,
1
1
)(
b)
n
n
xx
tt
,...,
,..,
1
1
)(
├
x
1
,…,x
n
Доказательство. а) Пусть y
1
,…,y
n
– попарно различные переменные, не входящие в
,
в t
1
,…,t
n
и отличных от x
1
,…,x
n
. Для k=1..n имеет место равенство:
k
k
k
k
k
k
xx
yy
nk
x
y
xx
yy
nk
xxxx
,...,
,...,
1
,...,
,...,
1
1
1
11
11
)(...))(...(
т.е. одновременная подстановка
совпадает с последовательной, (т.к. y
i
так выбраны) и выполнены все условия на
запись формулы. Тогда следующее дерево будет доказательством в ИПС
:
13
)(,...,,...,
13
13
)(,...,
)(,...,
14
14
)()(,
14
)()(
)()(
,...,
,...,11
,...,
,...,1
,...,
,...,1
,...,
,...,
,...,
,...,1
,...,
,...,
,...,
,...,
,...,
,...,
,...,
,...,
1
1
1
1
1
1
1
1
21
21
1
1
11
11
1
1
1
1
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
xx
yynn
xx
yynn
xx
yyn
xx
yy
xx
yynn
xx
yy
xx
yyn
xx
yy
xx
yy
yyxx
yxx
xx
xx
x
обозначим
n
n
xx
yy
,...,
,...,
1
1
)(
=. Для выполнено условие на запись
n
n
yy
tt
,...,
,...,
1
1
)(
и для всех k=1..n
k
k
k
k
k
k
yy
ttnk
y
t
yy
ttnk
yyyy
,...,
,...,1
,...,
,...,1
1
1
11
11
)(,...))(,...(
, тогда
)(14...14
)(,...,
)()(
,...,
,...,
1
,...,
,...,
,...,
,...,
1
1
1
1
1
1
разn
yy
n
n
n
n
n
n
yy
tt
n
yy
tt
yy
tt
т.е. секвенция
n
n
yy
tt
n
yy
,...,
,...,
1
1
1
)(,...,
доказуема.
Т.к.
n
n
n
n
xx
tt
yy
tt
,...,
,...,
,...,
,...,
1
1
1
1
)()(
, то доказана секвенция
n
n
n
n
xx
tt
xx
yy
n
yy
,...,
,...,
,...,
,...
1
1
1
1
1
)()(,...
. Осталось
применить правило сечения к данным секвенция:
в
xx
yyxxyy
n
n
n
n
n
n
n
n
xx
tt
n
xx
yy
nn
xx
tt
xx
yy
n
,12
)(,...,
)(,...,,...,)()(,...
,...,
,...,
1
,...,
,...,
11
,...,
,...,
,...,
,...
1
1
1
1
1
1
1
1
1
пункт b) доказать аналогично с помощью правил 15 и 16.
Предложение 4. В ИПС
допустимы правила а) …о) и
39
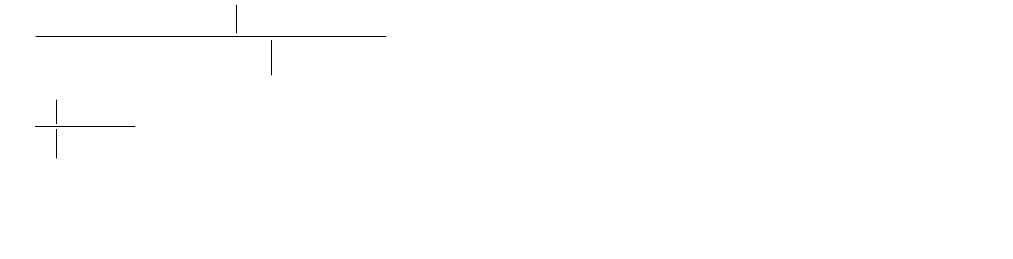
п)
n
n
n
n
n
n
xx
tt
xx
ttk
xx
tt
k
,...
,...,
,...
,...,
,...
,...,1
1
1
1
1
1
1
1
)()(,...,)(
,...,
(подстановка термов)
р)
x
t
x
)(
(удаление )
Доказательство. Первые 14 правил доказываются как и в ИС. Докажем правило п).
Будем использовать Предложение 3.
40
