Основы математической логики и теории алгоритмов
Подождите немного. Документ загружается.


1) из аксиомы 1
() и гипотезы получаем формулу ;
2) из аксиомы 1 () и гипотезы
получаем формулу ;
3) из заключения п. 1 и аксиомы ()(()(())) получаем
()(());
4) из заключения пп. 2 и 3 выводится формула ();
5) из гипотезы и заключения п. 4 получаем формулу .
Следствие. Тогда и только тогда
1
,... ,
n
├, когда ├(
1
(
2
…
(
n
)
…))
Доказательство. Пусть
1
,... ,
n
├. Тогда, применяя теорему о дедукции,
имеем
1
,... ,
n-1
├
n
. Аналогично, продолжая процесс необходимое число раз,
получаем ├(
1
(
2
…
(
n
)…)). Для доказательства достаточности
предположим, что ├, где
= (
1
(
2
…
(
n
)…)). Очевидно,
1
├
. По правилу
заключения получаем
1
├(
2
…
(
n
)…). Далее через n шагов имеем
1
,... ,
n
├.
Следующая теорема устанавливает эквивалентность доказуемости в ИС и
доказуемости в ИВ.
Теорема 2. (теорема об эквивалентности ИС и ИВ)
1. Секвенция
1
,... ,
n
├ доказуема в ИС тогда и только тогда, когда
формула
выводима в ИВ из формул
1
,... ,
n
.
2. Секвенция
1
,... ,
n
├ доказуема в ИС тогда и только тогда, когда
формула А А выводима в ИВ из формул
1
,... ,
n
.
Д о к а з а т е л ь с т в о . Так как доказуемость (тождественная истинность)
секвенций
1
,... ,
n
├·и
1
,... ,
n
├ равносильна доказуемости (соответственно
тождественной истинно
сти) формул
(
1
(
2
…
(
n
)…))) и (
1
(
2
…
(
n
А
А)…)) соответственно, в силу следствия достаточно показать, что
доказуемость формулы φ в ИС равносильна доказуемости формулы φ в ИВ.
Непосредственно проверяется, что все аксиомы ИВ тождественно истинны, а
правило заключения сохраняет тождественную истинность. Поэтому по теореме о
полноте из выводимости формулы φ в ИВ следует ее доказуемость в ИС.
Для доказательства выводимости в ИВ доказуемой в ИС формулы φ
достаточно проследить сохранение истинности утверждений ИВ, соответствующих
секвенциям, при переходе по любому из 12 правил вывода ИС. Сохранение
выводимости в ИВ для правил 1-5 устанавливается с помощью примера 2 и аксиом
21

3-7. Если в ИВ справедливо
1
,... ,
k
,
├ и
1
,... ,
k
,
├,
1
,... ,
k
├, то по
теореме о дедукции
1
,... ,
k
├
и
1
,... ,
k
├
. Применяя три раза правило
заключения к аксиоме 8, получаем
1
,... ,
k
├. Следовательно, правило 6
сохраняет выводимость. Правило 7 соответствует теореме о дедукции, а правило 8
— правилу заключения. Для доказательства сохранения выводимости правилом 9
рассмотрим справедливое в ИВ соотношение
1
,... ,
k
,
├A
A. Из аксиом 3 и 4
получаем
1
,... ,
k
,
├A и
1
,... ,
k
,
├A. По теореме о дедукции имеем
1
,... ,
k
├
A и
1
,... ,
k
├
A. Из аксиом 9 и 10 заключаем
1
,... ,
k
├
.
Рассмотрим правило 10. Если
1
,... ,
k
├
и
1
,... ,
k
├
, то из аксиомы 1
получаем
1
,... ,
k
├(AA)
и
1
,... ,
k
├(AA)
.
Из аксиом 9 и 10
заключаем
1
,... ,
k
├(AA),
. Сохранение выводимости по правилам 11 и 12
следует из определения вывода в ИВ.
Из теоремы 1.6.3. вытекает непротиворечивость и разрешимость ИВ.
Непосредственно проверяется независимость схем аксиом ИВ.
Множество формул Г называется противоречивым, если в ИВ справедливо
Г├ΑА. Если Г ― противоречивое множество формул, будем обозначать этот факт
через Г├.
На основании теоремы 2 справедливо следующее
Утверждение. Формула φ выводима в ИВ из множества формул Г тогда и
только тогда, когда множество Г{} ― противоречиво: Г├ Г{}├ .
1.7.
Алгоритмы проверки общезначимости и противоречивости в
ИВ
Здесь мы рассмотрим некоторые основные методы, которые используются для
исследования множеств формул исчислений ИС и ИВ на тождественную истинность
и противоречивость.
1. Алгоритм Квайна. Напомним, что формула φ от пропозициональных
переменных А
1
, А
2
, …, А
k
, является тождественно истинной, общезначимой или (что то
же самое) доказуемой, если булева функция f
φ
: {0, l}
k
{0,1}, соответствующая
формуле φ, тождественно равна 1. Для проверки значений функции f
используется
так называемое семантическое дерево, т. е. бинарное корневое дерево,
22
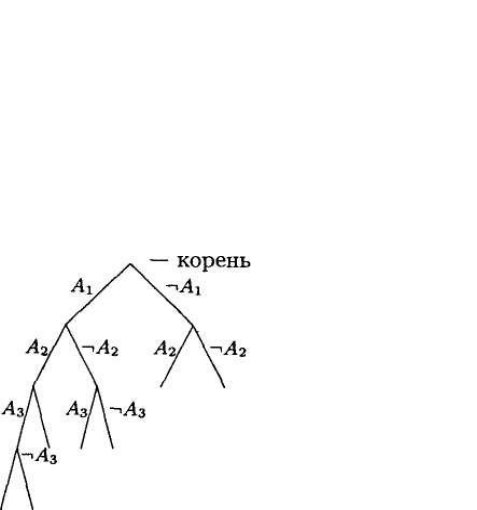
удовлетворяющее следующим условиям:
каждое ребро помечено литерой
j
i
А
;
литеры, выходящие из одной вершины, контрарны: A
i
,
A
i
,
ребра соответствуют литере одной и той же пропозициональной переменной А
i
тогда и только тогда, когда они находятся на одинаковом расстоянии от корня
(рис. 1).
Рис. 1
Семантическое дерево имеет 2
k
висячих вершин и для проверки
общезначимости необходимо пройти 2
к
маршрутов от корня до этих вершин.
Алгоритм Квайна позволяет проходить не все семантическое дерево, а только
его часть. Он состоит в том, что пропозициональным переменным А
i
, упорядоченным
в набор (Α
1
,Α
2
,··· A
k
), последовательно придаются значения 0 и 1 и
анализируются таблицы истинности формул, содержащих меньшее число
переменных.
П р и м е р 1. Проверить общезначимость формулы
=(((АВ)С)(АВ))(АС).
Упорядочим пропозициональные переменные в набор (А, В, С). Придадим
первой переменной А значение f(A) = 1. Тог да формула φ преобразуется следующим
образом: (((1В)С)(1В))(1С) ((ВС)В)С. В полученной формуле
переменной В придадим значение f(B) = 1. Тогда преобразованная формула примет
вид ((1С)1)С СС т. е. будет общезначимой. В случае f(B) = 0 имеем
((0С)0)С 0С, что также общезначимо. Рассмотрим теперь случай f(A) = 0.
Имеем
(0,B,C) = (((0В)С)(0В))(0С) 11 1 = 1. Таким образом, все
возможные случаи приводят к тождественно истинным формулам. Следовательно,
формула φ тождественно истинна. На рис. 2, изображено семантическое дерево,
23

соответствующее формуле
, а на рис. 3 ― часть семантического дерева, которая
фактически использовалась для проверки общезначимости.
Рис. 2
Рис. 3
2. Алгоритм редукции решает ту же задачу проверки общезначимости
формулы, но используется в том случае, когда в формуле содержится достаточно
много импликаций. Идея алгоритма состоит в попытке нахождения значений
пропозициональных переменных формулы φ, при которых значение функции f
равно
0, на основе того, что импликация является ложной в том и только в том случае, когда
посылка истинна, а заключение ложно.
Пример 2. Проверить тождественную истинность формулы φ =
((А
В)
С)
(А
(В
С)).
Предположим, что формула φ ложна при некотором наборе значений
переменных А, В, С. Тогда истинностная функция f по этим значениям переменных
дает следующие значения формул: f((А
В)
С) = 1, f(А
(В
С)).=0. Тогда из второго
равенства получаем f(А) = 1, f(B
С) =0, откуда имеем f(В) = 1, f(С) = 0. Однако при
этих значениях справедливо f((А
В)
С) = 0. Получили противоречие. Таким образом,
формула φ тождественно истинна.
3.Метод резолюций в ИВ. Пусть
ADDADD
2211
,
- дизъюнкты.
Дизъюнкт
21
DD
называется резольвентой дизъюнктов D
1
и D
2
no литере А и
обозначается через res
A
(D
1
,D
2
). Резольвентой дизъюнктов D
1
и D
2
называется их
резольвента по некоторой литере и обозначается через res(D
1
,D
2
)., res (А,А)= 0. В
последнем случае нуль будет отождествляться с формулой ΑΑ. Если дизъюнкты D
1
24
и D
2
не содержат контрарных литер, то резольвент у них не существует.
Пример 3. Если D
1
=A
B
C, D
2
=
A
B
D. res
A
(D
1,
D
2
)=B
C
B
D,
res
B
(D
1,
D
2
)=A
C
A
D, res
C
(D
1,
D
2
) не существует.
Предложение 1. 1. Если резольвента res(D
1,
D
2
) существует и не равна нулю,
то секвенция D
1,
D
2├
res(D
1,
D
2
) доказуема.
2. Если резольвента res(D
1,
D
2
) равна нулю, то доказуема секвенция D
1,
D
2├ .
.
Д о к а з а т е л ь с т в о п.2 очевидно в силу доказуемости секвенции А,
А├, где
А=D
1
,
А = D
2
. Для доказательства п. 1 рассмотрим дизъюнкты
ADDADD
2211
,
и их резольвенту res{D
1
,D
2
) =
21
DD
. Следующее дерево устанавливает доказуемость
секвенции D
1,
D
2├
res(D
1,
D
2
):
e
DDADAD
е
DDAAD
з
DDAA
АА
DDAD
DD
DDDAD
DD
2121
211
21211
11
2121
22
,
,
,
,
12,4
,
12,11,5
,
Пусть S = {D
1
,D
2
,..., D
m
} ― множество дизъюнктов. Последовательность формул
φ
1
,φ
2
,..., φ
n
называется резолютивным выводом из множества S, если для каждой
формулы φ
i
(i = 1,... ,n) выполняется какое-то из следующих условий:
φ
i
S;
существуют j,k < i такие, что φ
i
= res(
j
,
k
).
Теорема (теорема о полноте метода резолюций). Множество дизъюнктов S
противоречиво в том и только в том случае, когда существует резолютивный вывод
из S, заканчивающийся символом 0.
Доказательство. Противоречивость множества S при наличии резолютивного
вывода нуля вытекает из предложения 1. Существование резолютивного вывода нуля
из противоречивого множества дизъюнктов выходит за рамки курса.
Отметим, что метод резолюций можно использовать для проверки
выводимости формулы φ из данного множества формул
1
,…,
n
. Действительно,
условие
1
,…,
n
├
равносильно
условию
1
,…,
n
φ├, что в свою очередь
равносильно условию
├, где ψ =
1
…
n
φ. Приведем формулу ψ к ΚΗΦ:
=
D
1
…
D
m
, тогда
25

├ D
1
…
D
m├
D
1
,…,D
m├.
Таким образом, задача проверки выводимости φ
1
,... ,φ
n
\- φ сводится к
проверке противоречивости множества дизъюнктов S = { D
1
,…,D
m
}, что
равносильно существованию резолютивного вывода 0 из S.
Пример 4. Проверить методом резолюций доказуемость секвенции
A(BC), CDE, FDE├ A(DF).
Согласно утверждению выше нужно проверить на противоречивость
множество формул
S = {
A(BC), CDE, FDE,( A(DF))}. Приведем все формулы
из S к КНФ: S~ {ABC, CDE, FDE, (ABF)} ~ {ABC,
CDE, (FD)(FE), ABF}. Отсюда получаем множество дизъюнктов
S
={ABC, CDE, (FD), FE, A,B,F}.
Построим резолютивный вывод из
S
, заканчивающийся 0:
1)
res
А
(ABC,A) = BC;
2)
res
B
(BC,B) = C;
3)
res
D
(
CDE, FD) = CEF;
4)
res
Е
(CEF , FE) = CF;
5)
res
C
(CCF) = F;
6)
res(F,F) = 0.
Таким образом, по теореме о полноте метода резолюций множество S
противоречиво и, значит, данная секвенция доказуема.
Отметим, что метод резолюций достаточен для обнаружения возможной
выполнимости данного множества дизъюнктов S. Для этого включим в множество
S все дизъюнкты, получающиеся при резолютивных выводах из S. Из теоремы о
полноте метода резолюций вытекает
Следствие. Если множество S' состоит из всех элементов множества
дизъюнктов S, а также всевозможных резольвент всех своих элементов, то S
выполнимо тогда и только тогда, когда 0
S'.
Двойственным к правилу резолюций является правило согласия. Пусть K
1
= K
1
A,
K
2
= K
2
¬A — конъюнкты. Положим
A
res
(K
1
,K
2)
= K
1
K
2
,
res
(A,¬A)=1.
Аналогично задается вывод: пусть S = {Κ
1
,Κ
2
, ..., К
m
}― множество
26

конъюнктов. Последовательность формул
φ
1
, φ
2
, ..., φ
n
называется выводом из
множества S по правилу согласия, если для каждой формулы φ
i
(i = 1,... ,n) выполняется
какое-то из следующих условий:
φ
i
S;
существуют j,k < i такие, что φ
i
=
res
(
j
,
k
).
Теорема 4. Множество конъюнктов S = {Κ
1
,Κ
2
, ..., К
т
} общезначимо (т.е.
выполняется ├ Κ
1
Κ
2
...
К
т
) тогда и только тогда, когда существует вывод из
S по правилу согласия, заканчивающийся символом 1.
4.Метод резолюций для хорновских дизъюнктов.
В общем случае метод резолюций неэффективен, так как количество
переборов, которые необходимо сделать для получения ответа, экспоненциально
зависит от количества информации (числа дизъюнктов и переменных),
содержащейся в множестве дизъюнктов. Однако для некоторых классов
дизъюнктов, к которым относится класс так называемых хорновских дизъюнктов,
метод резолюций эффективен.
Дизъюнкт D называется хорновским, если он содержит не более одной
позитивной литеры.
Пример.5. Хорновскими дизъюнктами являются следующие дизъюнкты:
¬А¬В¬СЕ, ¬А¬С, ¬А, Е.
В общем случае хорновские дизъюнкты имеют вид ¬А
1
…¬А
n
В (что
эквивалентно формуле (А
1
…А
n
)В ) или ¬А
1
…¬А
n
. Хорновский дизъюнкт
вида ¬А
1
…¬А
n
В называется точным. При этом переменные Α
1
,...,Α
n
называются фактами, а переменная В ― целью. Хорновский дизъюнкт вида
¬А
1
…¬А
n
называется негативным. Дизъюнкт D = В называется унитарным
позитивным дизъюнктом.
Если S ― множество хорновских дизъюнктов, то невыполни
мость множества
S проверяется следующим образом. Выбираем в S унитарный позитивный дизъюнкт Ρ
и дизъюнкт D из S, содержащий ¬Ρ. После этого заменяем S на {S\{D}){геs(D,Р)} и
продолжаем процесс до тех пор, пока S не будет содержать 0 или не найдется
дизъюнктов P
И
D указанного вида. Если на заключительном шаге множество
дизъюнктов будет содержать 0, то исходное множество S противоречиво, в противном
27

случае S непротиворечиво.
Пример 6. Проверить на противоречивость множество дизъюнктов S = {Р
¬R
¬T, Q, R, T
¬P
¬R, T
¬Q, ¬P
¬Q
¬R}.
Для доказательства противоречивости запишем дизъюнкты из S
в таблицу и
применим описанный алгоритм, записывая результат каждого следующего шага в таблицу. Литеры, использующиеся на
данном шаге, будем подчеркивать.
№ шага
Р ¬R¬T
Q R
T¬P¬R
T¬Q ¬P¬Q¬R
1
Р ¬R¬T
Q R
T¬P¬R
T
¬P ¬R
2
P¬T
Q R
T¬P T ¬P
3
P
Q R
T¬P T ¬ P
4 0
На шаге 4 получаем 0, являющийся резолютивным выводом из S.
Следовательно, множество S невыполнимо.
Логические задачи
Аппарат исчислений высказываний позволяет решать так называемые
"логические" задачи. При этом самым трудным моментом является построение
"модели" задачи, т. е. выделение элементарных высказываний и сведение задачи к
проверке некоторых свойств высказываний, возникающих из условий задачи.
Пример 1. На следствии по делу о похищении автомобиля были допрошены
четыре гангстера ― Андре, Боб, Стив, Том. Андре сказал, что машину похитил Боб,
Боб утверждал, что виноват Том. Том заверил следователя, что Боб лжет. Стив
настаивал, что автомобиль угнал не он. Следователю удалось установить, что только
один из гангстеров сказал правду. Кто похитил автомобиль?
Решение. Обозначим высказывания "Андре украл", "Боб украл", "Стив украл",
"Том украл" через А, В, S и T соответственно. Тогда показания гангстеров имеют вид
В, Т, ¬Т, ¬S. Поскольку секвенция ├Т
¬T доказуема, или, что тоже самое, формула
Т
¬T тождественно истинна, то одно из утверждений ― Τ или ¬Т обязательно
истинно. Значит, Андре и Стив сказали ложь. Так как утверждение Стива "¬S" ложно,
то автомобиль украл Стив.
2. ЛОГИКА И ИСЧИСЛЕНИЯ ПРЕДИКАТОВ
В построенной выше логике высказываний в качестве исходных элементов
28

рассматриваются некоторые элементарные высказывания, из которых строятся
более сложные высказывания, называемые формулами. При этом не анализируются
структура и состав высказываний, а учитываются лишь значения истины или лжи,
которые они могут принимать. Однако имеется много предложений, которые не
могут быть рассмотрены таким простым способом. Например, приведем следующее
умозаключение:
Каждый человек смертен.
Сократ — человек, следовательно, он смертен.
Очевидно, рассмотренное рассуждение интуитивно корректно. Однако, введя
следующие обозначения:
Р: Каждый человек смертен,
Q: Сократ — человек,
R: Сократ смертен,
мы получаем формулу Ρ Q R, которая не доказуема в ИВ. Указанное
несоответствие между утверждениями имеет место потому, что в логике
высказываний не используется структура высказываний Р, Q и R. В этой главе мы
введем логику предикатов (логику первого порядка) и исчисления предикатов,
которые позволяют преодолевать подобные трудности и дают возможность
проводить формализацию большей части повседневного и математического языка.
Аналогично исчислению секвенций и исчислению высказываний мы будем
рассматривать два их расширения — секвенциальное исчисление предикатов данной
сигнатуры Σ (ИПС
) и исчисление предикатов гильбертовского типа ИП
.
Построение исчислений предикатов данной сигнатуры мы начнем с понятий
синтаксиса и семантики формулы, определения алгебраических систем (АС).
2.1. Алгебраические системы.
Формулы сигнатуры Σ.
Истинность формулы на алгебраической системе
Часто объектом изучения в математике служит множество с определенной на
нем структурой (к примеру, треугольники с отношением подобия), для уточнения
этого понятия введем определение АС.
29

Упорядочная тройка
=<P, F,
> называется сигнатурой, если выполняются
следующие условия:
a) Множества P и F не имеют общих элементов;
b) - отображение множества PF в .
Элементы P называются символами отношений или предикатами; F –символами
операций или функций. Отображение называется отображением местности или
арности для (валентность). Если (q)=n, то q – n-местный предикатный символ, если
qP, и q – n-местный функциональный символ, если qF. 0-местный функциональный
символ назовем символом константы или просто константой.
Часто конечную сигнатуру
=<P, F,
> будем представлять в виде =<p
1
(p
1
)
,...,p
n
(p
n
)
,...
f
1
(f
1
)
,..., f
k
(f
k
)
,...,c
1
,..c
m
..>=<P, F, C>(иногда с индексом)
Будем говорить, что содержится в
1
(
1
), если PP
1
, FF
1,
1.
Если PF, F= (P=), то называется предикатной (функциональной). Если
PF=, то назовем пустой.
Упорядочная пара A=<A,
A
> ( часто будем обозначать готическими буквами
A)называется алгебраической системой сигнатуры
, если выполняются следующие
условия:
a) А – непустое множество
b)
A
- отображение PF в множество отношений и операций на множестве А;
c) если pP, то
A
(p) является (p)-местным отношением на А;
d) если fF, то
A
(f) является (f)-местной операцией на А
Множество А назовем носителем A,
A
– интерпретацией сигнатуры в А. (далее
вместо
A
(p) будем обозначать p
A
или p, если ясно о какой A идет речь). Мощностью
АС A будем называть мощность ее носителя А( количество элементов).
Зафиксируем некоторую сигнатуру Σ и счетное множество V = {v
t
| i
ω},
элементы которого будем называть переменными и обозначать буквами х, у и z,
возможно, с индексами. Алфавит исчисления предикатов сигнатуры Σ (ИΠ
Σ
)
состоит из следующих групп символов:
30
